24.3 正多边形和圆 分层练习 (含答案)2023-2024学年数学人教版九年级上册
文档属性
| 名称 | 24.3 正多边形和圆 分层练习 (含答案)2023-2024学年数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 236.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 15:17:59 | ||
图片预览


文档简介
24.3 正多边形和圆
【练基础】
必备知识1 正多边形的有关概念
1.下列命题中正确的是 ( )
A.各边相等的多边形是正多边形
B.各内角分别相等的多边形是正多边形
C.既是轴对称图形又是中心对称图形的多边形是正多边形
D.各边相等,各角也相等的多边形是正多边形
2.对于一个正多边形,下列四个命题中,错误的是 ( )
A.正多边形是轴对称图形,每条边的垂直平分线是它的对称轴
B.正多边形是中心对称图形,正多边形的中心是它的对称中心
C.正多边形每一个外角都等于正多边形的中心角
D.正多边形每一个内角都与正多边形的中心角互补
必备知识2 圆内接正多边形的有关概念及计算
3.一个圆内接正多边形的边所对的圆心角为45°,则这个正多边形的边数是 ( )
A.6 B.7 C.8 D.9
4. 有一个边长为50 cm的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为 ( )
A.50 cm B.25 cm
C.50 cm D.50 cm
5.正多边形的一边所对的中心角与该正多边形的一个内角的关系是 ( )
A.互余 B.互补
C.互余或互补 D.不能确定
6.【沧州期中】嘉淇用一些完全相同的△ABC纸片拼接图案,已知用6个△ABC纸片按图1所示的方式拼接可得外轮廓是正六边形的图案.如果用若干个△ABC纸片按图2所示的方式拼接,那么可以得到外轮廓的图案是 ( )
A.正十二边形 B.正十边形
C.正九边形 D.正八边形
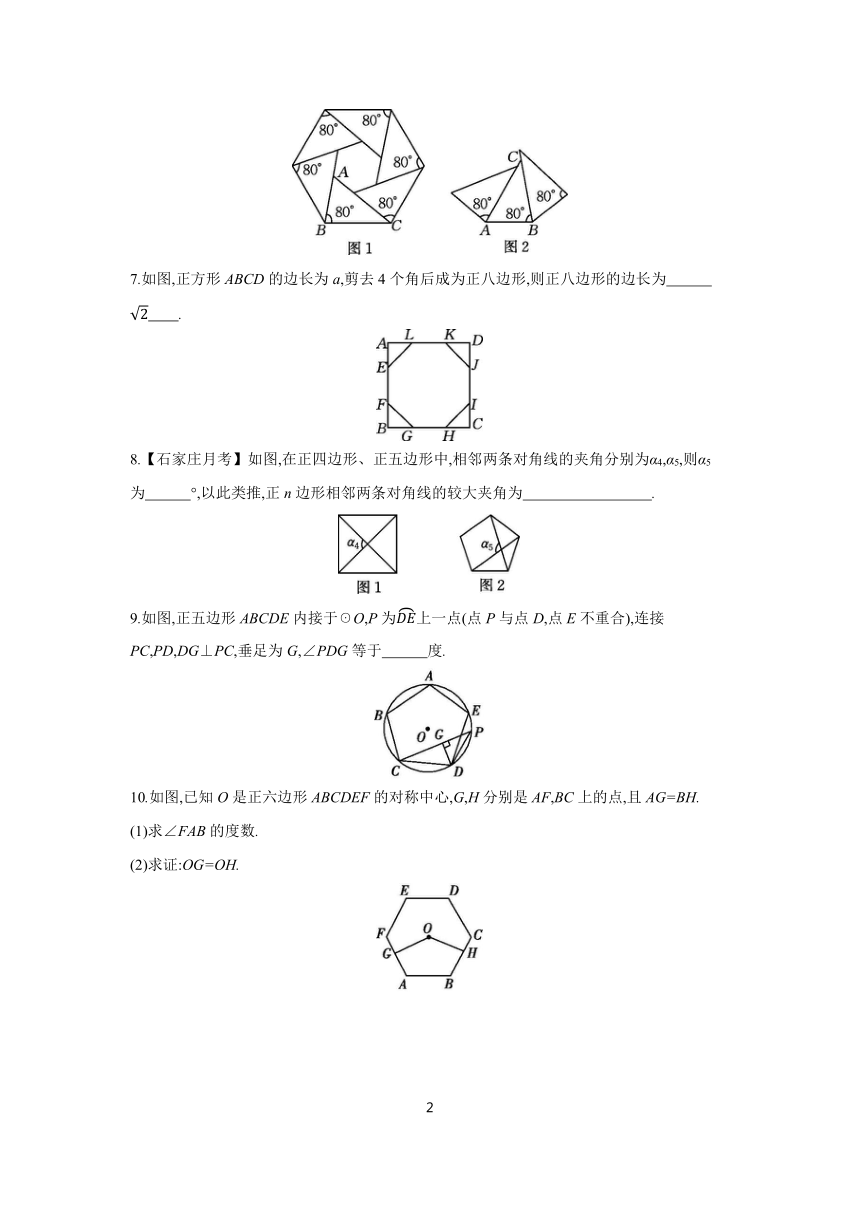
7.如图,正方形ABCD的边长为a,剪去4个角后成为正八边形,则正八边形的边长为 .
8.【石家庄月考】如图,在正四边形、正五边形中,相邻两条对角线的夹角分别为α4,α5,则α5为 °,以此类推,正n边形相邻两条对角线的较大夹角为 .
9.如图,正五边形ABCDE内接于☉O,P为上一点(点P与点D,点E不重合),连接PC,PD,DG⊥PC,垂足为G,∠PDG等于 度.
10.如图,已知O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH.
(1)求∠FAB的度数.
(2)求证:OG=OH.
必备知识3 正多边形的作法
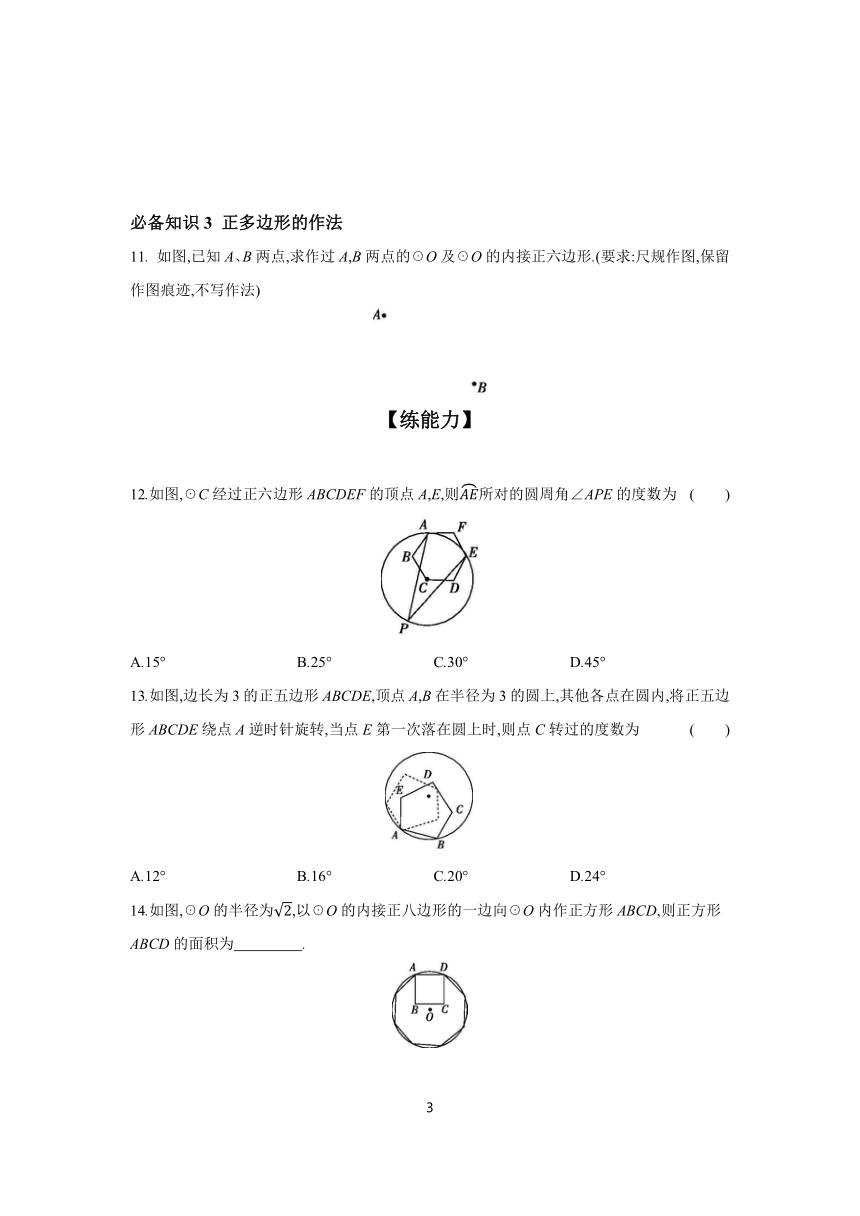
11. 如图,已知A、B两点,求作过A,B两点的☉O及☉O的内接正六边形.(要求:尺规作图,保留作图痕迹,不写作法)
【练能力】
12.如图,☉C经过正六边形ABCDEF的顶点A,E,则所对的圆周角∠APE的度数为 ( )
A.15° B.25° C.30° D.45°
13.如图,边长为3的正五边形ABCDE,顶点A,B在半径为3的圆上,其他各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为 ( )
A.12° B.16° C.20° D.24°
14.如图,☉O的半径为,以☉O的内接正八边形的一边向☉O内作正方形ABCD,则正方形ABCD的面积为 .
15.如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=3,EF=4,FC=5,求正方形ABCD的外接圆的半径.
【练素养】
16.(1)如图1,△ABC是☉O的内接正三角形,P为劣弧BC上一动点,求证:PA=PB+PC.
(2)如图2,四边形ABCD是☉O的内接正方形,P为劣弧BC上一动点,求证:PA=PC+PB.
(3)如图3,六边形ABCDEF是☉O的内接正六边形,P为劣弧BC上一动点,直接写出PA,PB,PC三者之间的数量关系.
参考答案
练基础
1.D 2.B 3.C 4.C 5.B 6.C 7.(-1)a
8.108 【解析】如图,由正方形ABCD可得AC⊥BD,
∴α4=90°.
由正五边形ABCDE可得AB=BC=CD,∠ABC=∠BCD=108°,
∴∠DBC=∠ACB==36°,
∴α5=180°-∠DBC-∠ACB=108°.
同理可得α6=120°.
∴正n边形相邻两条对角线的夹角αn=,
故答案为108;.
9.54
10.【解析】(1)∵六边形ABCDEF是正六边形,
∴∠FAB==120°.
(2)证明:如图,连接OA,OB.
∵OA=OB,
∴∠OAB=∠OBA.
∵∠FAB=∠CBA,
∴∠OAG=∠OBH.
在△AOG和△BOH中,
∴△AOG≌△BOH(SAS),
∴OG=OH.
11.【解析】(答案不唯一)如图,☉O及☉O的内接正六边形即所求.
练能力
12.C 13.A 14.4-2
15.【解析】如图,连接AC,则AC是该圆的直径,延长AE交圆于点G,
连接CG,则∠AGC=90°.
∵AE⊥EF,EF⊥FC,
∴四边形EFCG是矩形,
∴EG=FC=5,GC=EF=4,
∴AG=8.
由勾股定理得AC==4,
∴正方形ABCD的外接圆的半径为2.
练素养
16.【解析】(1)证明:如图1,连接BP并延长至点E,使PE=PC,连接CE.
∵四边形ABPC是☉O的内接四边形,
∴∠BAC+∠BPC=180°.
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°.
∵PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°.
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP.
∵△ABC,△ECP为等边三角形,
∴CE=PC,AC=BC.
在△BEC和△APC中,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC.
(2)证明:如图2,连接BP,过点B作BE⊥PB交PA于点E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∴∠APB=45°,
∴BP=BE,
∴PE=PB.
在△ABE和△CBP中,
∴△ABE≌△CBP(SAS),
∴PC=AE,∴PA=AE+PE=PC+PB.
(3)PA=PC+PB.
提示:如图3,连接PC,PB,过点B作BM⊥AP,在AP上截取AQ=PC,连接BQ.
∵∠BAP=∠BCP,AB=BC,
在△ABQ和△CBP中,
∴△ABQ≌△CBP(SAS),
∴BQ=BP,
∴MP=QM.
又∵∠APB=30°,
∴PM=PB,
∴PQ=PB,
∴PA=AQ+PQ=PC+PB.
2
【练基础】
必备知识1 正多边形的有关概念
1.下列命题中正确的是 ( )
A.各边相等的多边形是正多边形
B.各内角分别相等的多边形是正多边形
C.既是轴对称图形又是中心对称图形的多边形是正多边形
D.各边相等,各角也相等的多边形是正多边形
2.对于一个正多边形,下列四个命题中,错误的是 ( )
A.正多边形是轴对称图形,每条边的垂直平分线是它的对称轴
B.正多边形是中心对称图形,正多边形的中心是它的对称中心
C.正多边形每一个外角都等于正多边形的中心角
D.正多边形每一个内角都与正多边形的中心角互补
必备知识2 圆内接正多边形的有关概念及计算
3.一个圆内接正多边形的边所对的圆心角为45°,则这个正多边形的边数是 ( )
A.6 B.7 C.8 D.9
4. 有一个边长为50 cm的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为 ( )
A.50 cm B.25 cm
C.50 cm D.50 cm
5.正多边形的一边所对的中心角与该正多边形的一个内角的关系是 ( )
A.互余 B.互补
C.互余或互补 D.不能确定
6.【沧州期中】嘉淇用一些完全相同的△ABC纸片拼接图案,已知用6个△ABC纸片按图1所示的方式拼接可得外轮廓是正六边形的图案.如果用若干个△ABC纸片按图2所示的方式拼接,那么可以得到外轮廓的图案是 ( )
A.正十二边形 B.正十边形
C.正九边形 D.正八边形
7.如图,正方形ABCD的边长为a,剪去4个角后成为正八边形,则正八边形的边长为 .
8.【石家庄月考】如图,在正四边形、正五边形中,相邻两条对角线的夹角分别为α4,α5,则α5为 °,以此类推,正n边形相邻两条对角线的较大夹角为 .
9.如图,正五边形ABCDE内接于☉O,P为上一点(点P与点D,点E不重合),连接PC,PD,DG⊥PC,垂足为G,∠PDG等于 度.
10.如图,已知O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH.
(1)求∠FAB的度数.
(2)求证:OG=OH.
必备知识3 正多边形的作法
11. 如图,已知A、B两点,求作过A,B两点的☉O及☉O的内接正六边形.(要求:尺规作图,保留作图痕迹,不写作法)
【练能力】
12.如图,☉C经过正六边形ABCDEF的顶点A,E,则所对的圆周角∠APE的度数为 ( )
A.15° B.25° C.30° D.45°
13.如图,边长为3的正五边形ABCDE,顶点A,B在半径为3的圆上,其他各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为 ( )
A.12° B.16° C.20° D.24°
14.如图,☉O的半径为,以☉O的内接正八边形的一边向☉O内作正方形ABCD,则正方形ABCD的面积为 .
15.如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=3,EF=4,FC=5,求正方形ABCD的外接圆的半径.
【练素养】
16.(1)如图1,△ABC是☉O的内接正三角形,P为劣弧BC上一动点,求证:PA=PB+PC.
(2)如图2,四边形ABCD是☉O的内接正方形,P为劣弧BC上一动点,求证:PA=PC+PB.
(3)如图3,六边形ABCDEF是☉O的内接正六边形,P为劣弧BC上一动点,直接写出PA,PB,PC三者之间的数量关系.
参考答案
练基础
1.D 2.B 3.C 4.C 5.B 6.C 7.(-1)a
8.108 【解析】如图,由正方形ABCD可得AC⊥BD,
∴α4=90°.
由正五边形ABCDE可得AB=BC=CD,∠ABC=∠BCD=108°,
∴∠DBC=∠ACB==36°,
∴α5=180°-∠DBC-∠ACB=108°.
同理可得α6=120°.
∴正n边形相邻两条对角线的夹角αn=,
故答案为108;.
9.54
10.【解析】(1)∵六边形ABCDEF是正六边形,
∴∠FAB==120°.
(2)证明:如图,连接OA,OB.
∵OA=OB,
∴∠OAB=∠OBA.
∵∠FAB=∠CBA,
∴∠OAG=∠OBH.
在△AOG和△BOH中,
∴△AOG≌△BOH(SAS),
∴OG=OH.
11.【解析】(答案不唯一)如图,☉O及☉O的内接正六边形即所求.
练能力
12.C 13.A 14.4-2
15.【解析】如图,连接AC,则AC是该圆的直径,延长AE交圆于点G,
连接CG,则∠AGC=90°.
∵AE⊥EF,EF⊥FC,
∴四边形EFCG是矩形,
∴EG=FC=5,GC=EF=4,
∴AG=8.
由勾股定理得AC==4,
∴正方形ABCD的外接圆的半径为2.
练素养
16.【解析】(1)证明:如图1,连接BP并延长至点E,使PE=PC,连接CE.
∵四边形ABPC是☉O的内接四边形,
∴∠BAC+∠BPC=180°.
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°.
∵PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°.
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP.
∵△ABC,△ECP为等边三角形,
∴CE=PC,AC=BC.
在△BEC和△APC中,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC.
(2)证明:如图2,连接BP,过点B作BE⊥PB交PA于点E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∴∠APB=45°,
∴BP=BE,
∴PE=PB.
在△ABE和△CBP中,
∴△ABE≌△CBP(SAS),
∴PC=AE,∴PA=AE+PE=PC+PB.
(3)PA=PC+PB.
提示:如图3,连接PC,PB,过点B作BM⊥AP,在AP上截取AQ=PC,连接BQ.
∵∠BAP=∠BCP,AB=BC,
在△ABQ和△CBP中,
∴△ABQ≌△CBP(SAS),
∴BQ=BP,
∴MP=QM.
又∵∠APB=30°,
∴PM=PB,
∴PQ=PB,
∴PA=AQ+PQ=PC+PB.
2
同课章节目录
