2023-2024学年数学人教版九年级上册24.4 课时1 弧长和扇形面积 分层练习(含解析)
文档属性
| 名称 | 2023-2024学年数学人教版九年级上册24.4 课时1 弧长和扇形面积 分层练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 144.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 15:18:40 | ||
图片预览


文档简介
24.4 课时1 弧长和扇形面积
【练基础】
必备知识1 弧长公式
1.已知圆心角是60°,半径为30的扇形的弧长为 ( )
A.5π B.10π C.20π D.25π
2.扇形的弧长为6π,半径为9,则扇形的圆心角为 ( )
A.100° B.120° C.135° D.150°
必备知识2 扇形面积公式
3. 已知一个扇形的半径是2,圆心角是60°,则这个扇形的面积是 ( )
A. B.π C. D.2π
4.已知一个扇形的弧长为π,半径是3,则这个扇形的面积为 ( )
A.π B. C. D.3π
必备知识3 利用扇形面积计算阴影部分面积
5.如图,在☉O中,OA=2,∠C=45°,则图中阴影部分的面积为 ( )
A.- B.π-
C.-2 D.π-2
6.如图,在矩形ABCD中,AB=1,AD=2,以A为圆心,AD的长为半径作弧交BC于点D',则图中阴影部分的面积为 ( )
A.π B. C. D.
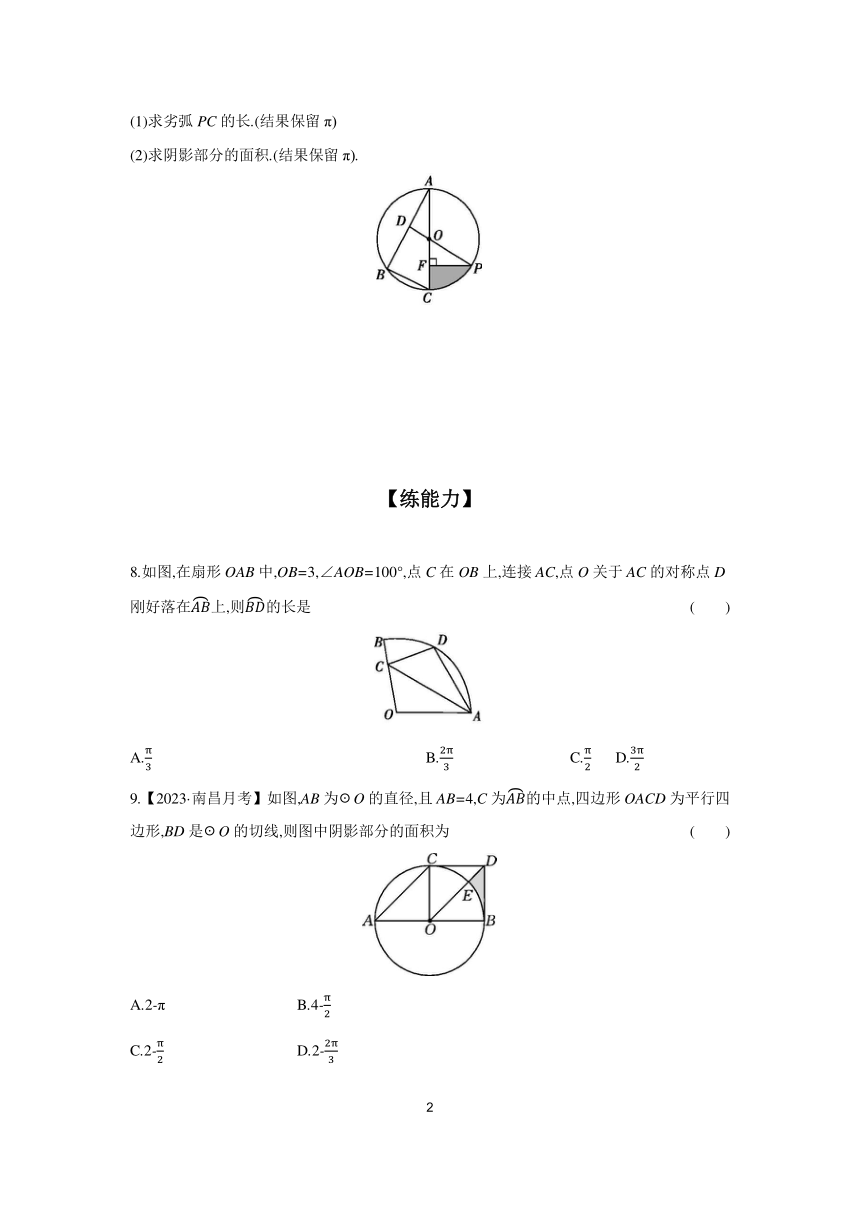
7.如图,已知☉O是△ABC的外接圆,AC是直径,∠A=30°,BC=2,D是AB的中点,连接DO并延长交☉O于点P,过点P作PF⊥AC于点F.
(1)求劣弧PC的长.(结果保留π)
(2)求阴影部分的面积.(结果保留π).
【练能力】
8.如图,在扇形OAB中,OB=3,∠AOB=100°,点C在OB上,连接AC,点O关于AC的对称点D刚好落在上,则的长是 ( )
A. B. C. D.
9.【2023·南昌月考】如图,AB为☉O的直径,且AB=4,C为的中点,四边形OACD为平行四边形,BD是☉O的切线,则图中阴影部分的面积为 ( )
A.2-π B.4-
C.2- D.2-
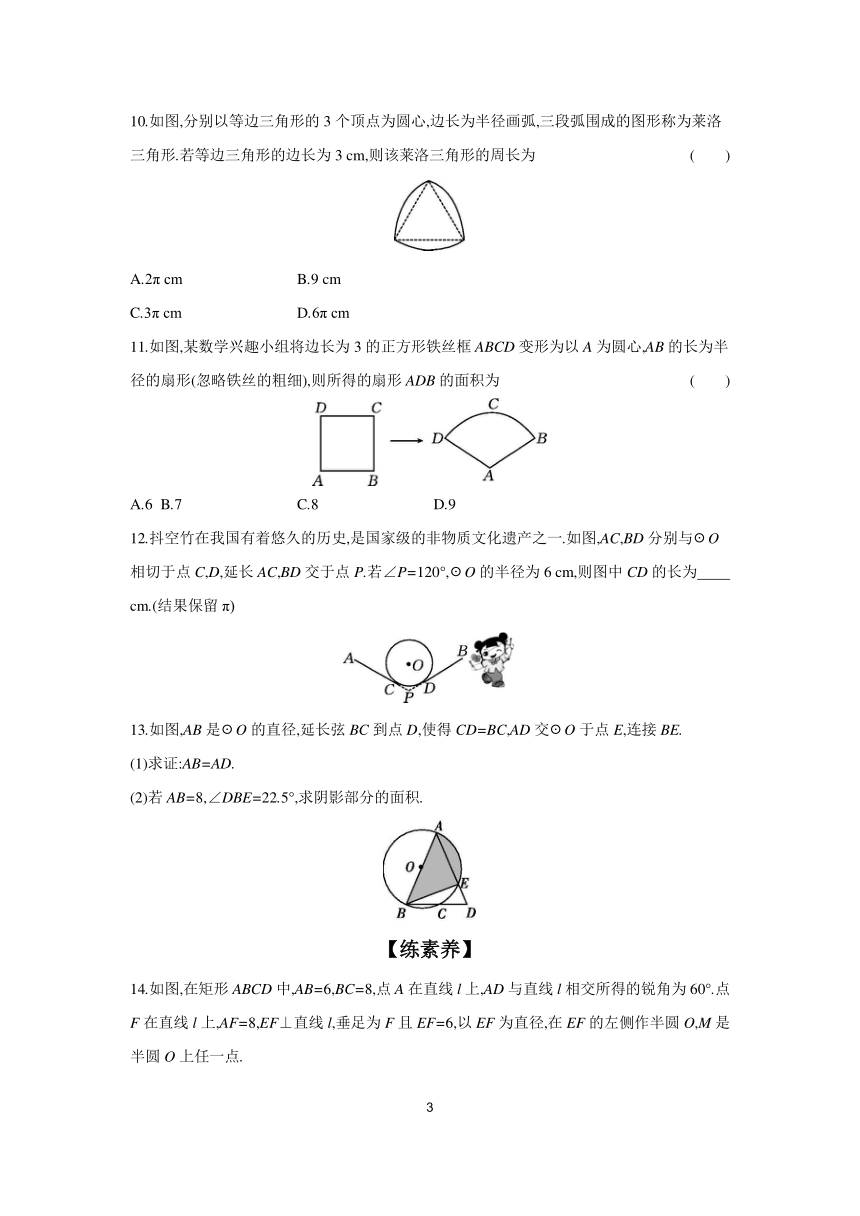
10.如图,分别以等边三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若等边三角形的边长为3 cm,则该莱洛三角形的周长为 ( )
A.2π cm B.9 cm
C.3π cm D.6π cm
11.如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB的长为半径的扇形(忽略铁丝的粗细),则所得的扇形ADB的面积为 ( )
A.6 B.7 C.8 D.9
12.抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC,BD分别与☉O相切于点C,D,延长AC,BD交于点P.若∠P=120°,☉O的半径为6 cm,则图中CD的长为 cm.(结果保留π)
13.如图,AB是☉O的直径,延长弦BC到点D,使得CD=BC,AD交☉O于点E,连接BE.
(1)求证:AB=AD.
(2)若AB=8,∠DBE=22.5°,求阴影部分的面积.
【练素养】
14.如图,在矩形ABCD中,AB=6,BC=8,点A在直线l上,AD与直线l相交所得的锐角为60°.点F在直线l上,AF=8,EF⊥直线l,垂足为F且EF=6,以EF为直径,在EF的左侧作半圆O,M是半圆O上任一点.
发现:AM的最小值为 ,AM的最大值为 ,OB与直线l的位置关系是 .
思考:矩形ABCD保持不动,半圆O沿直线l向左平移,当点E落在AD边上时,求半圆与矩形重合部分的周长和面积.
参考答案
练基础
1.B 2.B 3.A 4.C 5.D 6.C
7.【解析】(1)∵D是AB的中点,PD经过圆心,
∴PD⊥AB.
∵∠A=30°,
∴∠POC=∠AOD=60°,OA=2OD.
∵PF⊥AC,
∴∠OPF=30°,
∴OF=OP.
∵OA=OC,AD=BD,
∴BC=2OD,
∴OA=BC=2,
∴☉O的半径为2,
∴劣弧PC的长===π.
(2)∵OF=OP,
∴OF=1,
∴PF==,
∴S阴影=S扇形-S△OPF=-×1×= π-.
练能力
8.B
9.C 【解析】∵AB为☉O的直径,且AB=4,C为的中点,
∴=,
∴∠AOC=∠BOC=90°.
∵OA=OC.
∴∠A=45°.
∵四边形OACD为平行四边形,
∴AC∥OD,
∴∠DOB=∠A=45°.
∵BD是☉O的切线,
∴∠OBD=90°,
∴△OBD是等腰直角三角形,
∴OB=BD=2,
∴图中阴影部分的面积=△OBD的面积-扇形BOE的面积=×2×2-=2-.
故选C.
10.C 11.D 12.2π
13.【解析】(1)证明:如图,连接AC.
∵AB为☉O直径,
∴AC⊥BC.
又∵BC=CD,
∴AC垂直平分BD,
∴AB=AD.
(2)如图,连接OE.
∵AB=AD,
∴∠ABD=∠D.
∵AB为☉O的直径,
∴∠BED=90°.
∵∠DBE=22.5°,
∴∠D=67.5°=∠ABC,
∴∠ABE=45°.
∵OE=OB,
∴∠OEB=∠ABE=45°,
∴∠AOE=∠OEB+∠ABE=45°+45°=90°.
∵AB=8,
∴BO=EO=4,
∴S阴影=S△BOE+S扇形OAE=×4×4+=8+4π.
练素养
14.【解析】发现:-3;10;平行.
提示:由题意可知,OM=OF=3,AF=8,EF⊥l,
∴OA===.
当点M在线段OA上时,AM有最小值,最小值为-3.
当点M与点E重合时,AM有最大值,最大值==10.
如图1,过点B作BG⊥l,垂足为G,连接BO.
∵∠DAF=60°,∠BAD=90°,
∴∠BAG=30°.
∵GB=AB=3.
∴OF=BG=3.
又∵GB∥OF,
∴四边形OBGF为平行四边形,
∴OB∥FG,即OB∥l.
故答案为-3;10;平行.
思考:如图2,连接OG,过点O作OH⊥EG.
∵∠DAF=60°,EF⊥AF,
∴∠AEF=30°,
∴∠GOE=120°,
∴GE=2EH=2××3=3,
∴C重合部分=+3=2π+3,
∴S重合部分=S扇形GOE-S△GOE=-3××=3π-.
2
【练基础】
必备知识1 弧长公式
1.已知圆心角是60°,半径为30的扇形的弧长为 ( )
A.5π B.10π C.20π D.25π
2.扇形的弧长为6π,半径为9,则扇形的圆心角为 ( )
A.100° B.120° C.135° D.150°
必备知识2 扇形面积公式
3. 已知一个扇形的半径是2,圆心角是60°,则这个扇形的面积是 ( )
A. B.π C. D.2π
4.已知一个扇形的弧长为π,半径是3,则这个扇形的面积为 ( )
A.π B. C. D.3π
必备知识3 利用扇形面积计算阴影部分面积
5.如图,在☉O中,OA=2,∠C=45°,则图中阴影部分的面积为 ( )
A.- B.π-
C.-2 D.π-2
6.如图,在矩形ABCD中,AB=1,AD=2,以A为圆心,AD的长为半径作弧交BC于点D',则图中阴影部分的面积为 ( )
A.π B. C. D.
7.如图,已知☉O是△ABC的外接圆,AC是直径,∠A=30°,BC=2,D是AB的中点,连接DO并延长交☉O于点P,过点P作PF⊥AC于点F.
(1)求劣弧PC的长.(结果保留π)
(2)求阴影部分的面积.(结果保留π).
【练能力】
8.如图,在扇形OAB中,OB=3,∠AOB=100°,点C在OB上,连接AC,点O关于AC的对称点D刚好落在上,则的长是 ( )
A. B. C. D.
9.【2023·南昌月考】如图,AB为☉O的直径,且AB=4,C为的中点,四边形OACD为平行四边形,BD是☉O的切线,则图中阴影部分的面积为 ( )
A.2-π B.4-
C.2- D.2-
10.如图,分别以等边三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若等边三角形的边长为3 cm,则该莱洛三角形的周长为 ( )
A.2π cm B.9 cm
C.3π cm D.6π cm
11.如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB的长为半径的扇形(忽略铁丝的粗细),则所得的扇形ADB的面积为 ( )
A.6 B.7 C.8 D.9
12.抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC,BD分别与☉O相切于点C,D,延长AC,BD交于点P.若∠P=120°,☉O的半径为6 cm,则图中CD的长为 cm.(结果保留π)
13.如图,AB是☉O的直径,延长弦BC到点D,使得CD=BC,AD交☉O于点E,连接BE.
(1)求证:AB=AD.
(2)若AB=8,∠DBE=22.5°,求阴影部分的面积.
【练素养】
14.如图,在矩形ABCD中,AB=6,BC=8,点A在直线l上,AD与直线l相交所得的锐角为60°.点F在直线l上,AF=8,EF⊥直线l,垂足为F且EF=6,以EF为直径,在EF的左侧作半圆O,M是半圆O上任一点.
发现:AM的最小值为 ,AM的最大值为 ,OB与直线l的位置关系是 .
思考:矩形ABCD保持不动,半圆O沿直线l向左平移,当点E落在AD边上时,求半圆与矩形重合部分的周长和面积.
参考答案
练基础
1.B 2.B 3.A 4.C 5.D 6.C
7.【解析】(1)∵D是AB的中点,PD经过圆心,
∴PD⊥AB.
∵∠A=30°,
∴∠POC=∠AOD=60°,OA=2OD.
∵PF⊥AC,
∴∠OPF=30°,
∴OF=OP.
∵OA=OC,AD=BD,
∴BC=2OD,
∴OA=BC=2,
∴☉O的半径为2,
∴劣弧PC的长===π.
(2)∵OF=OP,
∴OF=1,
∴PF==,
∴S阴影=S扇形-S△OPF=-×1×= π-.
练能力
8.B
9.C 【解析】∵AB为☉O的直径,且AB=4,C为的中点,
∴=,
∴∠AOC=∠BOC=90°.
∵OA=OC.
∴∠A=45°.
∵四边形OACD为平行四边形,
∴AC∥OD,
∴∠DOB=∠A=45°.
∵BD是☉O的切线,
∴∠OBD=90°,
∴△OBD是等腰直角三角形,
∴OB=BD=2,
∴图中阴影部分的面积=△OBD的面积-扇形BOE的面积=×2×2-=2-.
故选C.
10.C 11.D 12.2π
13.【解析】(1)证明:如图,连接AC.
∵AB为☉O直径,
∴AC⊥BC.
又∵BC=CD,
∴AC垂直平分BD,
∴AB=AD.
(2)如图,连接OE.
∵AB=AD,
∴∠ABD=∠D.
∵AB为☉O的直径,
∴∠BED=90°.
∵∠DBE=22.5°,
∴∠D=67.5°=∠ABC,
∴∠ABE=45°.
∵OE=OB,
∴∠OEB=∠ABE=45°,
∴∠AOE=∠OEB+∠ABE=45°+45°=90°.
∵AB=8,
∴BO=EO=4,
∴S阴影=S△BOE+S扇形OAE=×4×4+=8+4π.
练素养
14.【解析】发现:-3;10;平行.
提示:由题意可知,OM=OF=3,AF=8,EF⊥l,
∴OA===.
当点M在线段OA上时,AM有最小值,最小值为-3.
当点M与点E重合时,AM有最大值,最大值==10.
如图1,过点B作BG⊥l,垂足为G,连接BO.
∵∠DAF=60°,∠BAD=90°,
∴∠BAG=30°.
∵GB=AB=3.
∴OF=BG=3.
又∵GB∥OF,
∴四边形OBGF为平行四边形,
∴OB∥FG,即OB∥l.
故答案为-3;10;平行.
思考:如图2,连接OG,过点O作OH⊥EG.
∵∠DAF=60°,EF⊥AF,
∴∠AEF=30°,
∴∠GOE=120°,
∴GE=2EH=2××3=3,
∴C重合部分=+3=2π+3,
∴S重合部分=S扇形GOE-S△GOE=-3××=3π-.
2
同课章节目录
