第二十三章 旋转 分层练习(含答案) 2023-2024学年数学人教版九年级上册
文档属性
| 名称 | 第二十三章 旋转 分层练习(含答案) 2023-2024学年数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 242.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-16 00:00:00 | ||
图片预览


文档简介
第二十三章 旋转 自我评估
(建议用时:80分钟 分值:60分)
一、选择题(本大题共6小题,每小题3分,满分18分)
1.下列图案是我国部分博物馆标志,其中既是轴对称图形又是中心对称图形的是 ( )
A B C D
2.如图,五角星的五个顶点等分圆周,把这个图形绕着圆心顺时针旋转一定的角度后能与自身重合,那么这个角度至少为 ( )
A.60° B.72° C.75° D.90°
3.下列现象中:①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.属于旋转的有 ( )
A.2个 B.3个 C.4个 D.5个
4.点P(2a+1,4)与P'(1,3b-1)关于原点对称,则2a+b的值为 ( )
A.3 B.-2 C.-3 D.2
5.把点P(x,y)绕原点顺时针旋转270°,点P的对应点的坐标是 ( )
A.(y,-x) B.(-x,-y)
C.(-y,x) D.(x,y)
6.如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是 ( )
A.-1 B.-2
C.2 -1 D.2-2
二、填空题(本大题共3小题,每小题3分,满分9分)
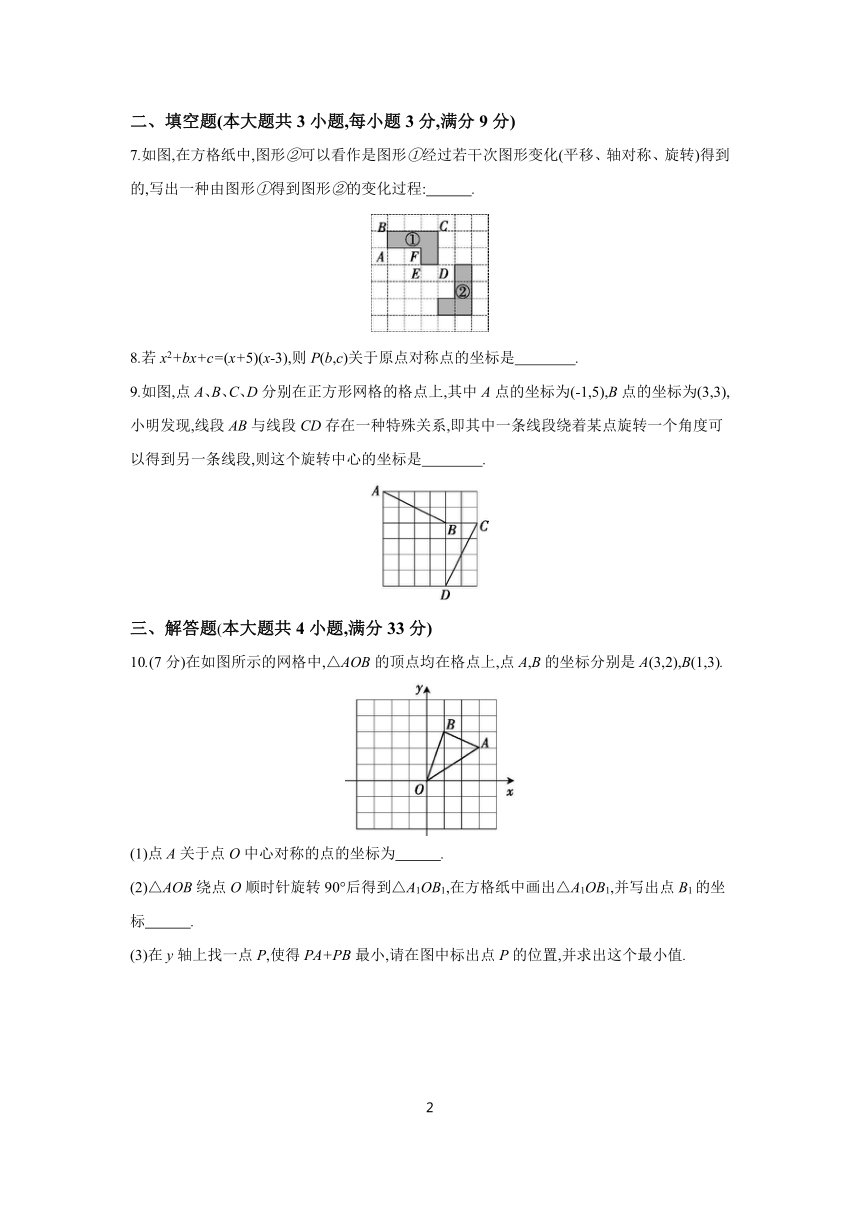
7.如图,在方格纸中,图形②可以看作是图形①经过若干次图形变化(平移、轴对称、旋转)得到的,写出一种由图形①得到图形②的变化过程: .
8.若x2+bx+c=(x+5)(x-3),则P(b,c)关于原点对称点的坐标是 .
9.如图,点A、B、C、D分别在正方形网格的格点上,其中A点的坐标为(-1,5),B点的坐标为(3,3),小明发现,线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标是 .
三、解答题(本大题共4小题,满分33分)
10.(7分)在如图所示的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,2),B(1,3).
(1)点A关于点O中心对称的点的坐标为 .
(2)△AOB绕点O顺时针旋转90°后得到△A1OB1,在方格纸中画出△A1OB1,并写出点B1的坐标 .
(3)在y轴上找一点P,使得PA+PB最小,请在图中标出点P的位置,并求出这个最小值.
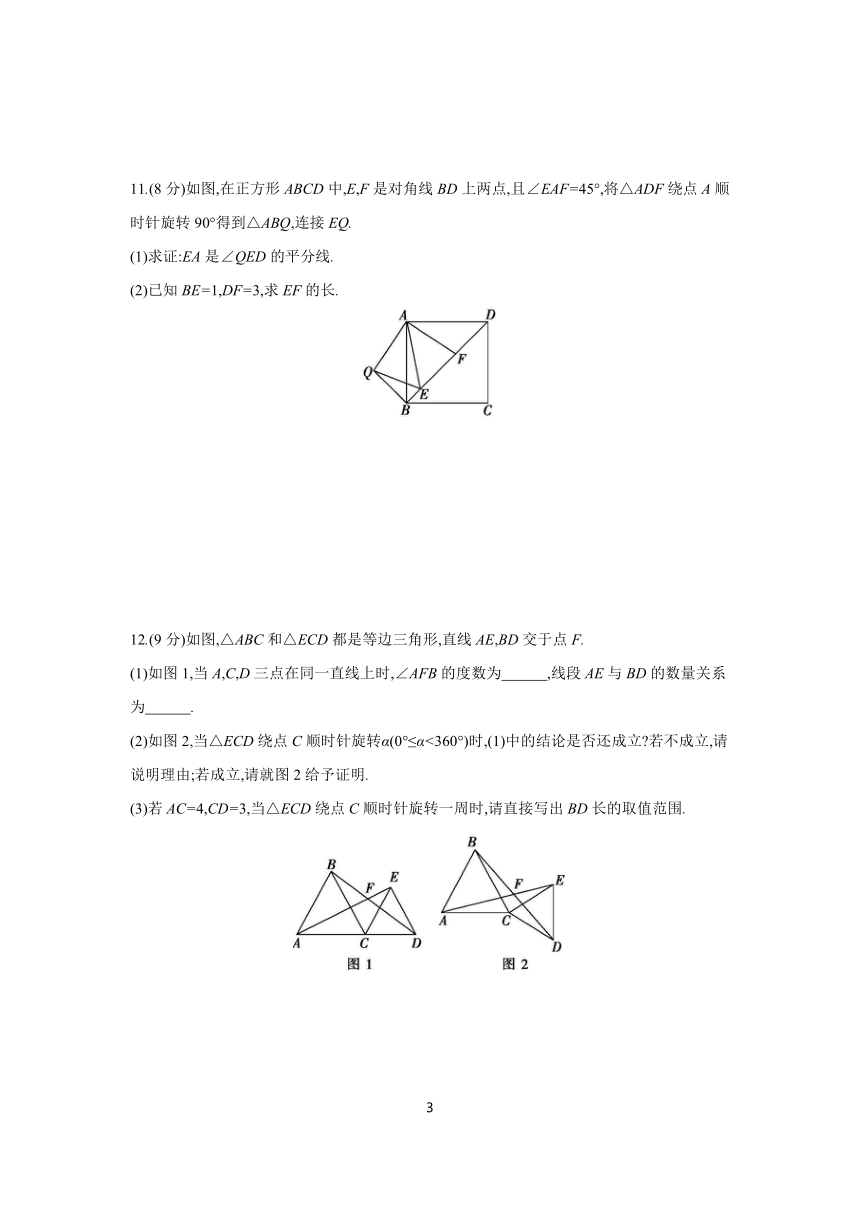
11.(8分)如图,在正方形ABCD中,E,F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°得到△ABQ,连接EQ.
(1)求证:EA是∠QED的平分线.
(2)已知BE=1,DF=3,求EF的长.
12.(9分)如图,△ABC和△ECD都是等边三角形,直线AE,BD交于点F.
(1)如图1,当A,C,D三点在同一直线上时,∠AFB的度数为 ,线段AE与BD的数量关系为 .
(2)如图2,当△ECD绕点C顺时针旋转α(0°≤α<360°)时,(1)中的结论是否还成立 若不成立,请说明理由;若成立,请就图2给予证明.
(3)若AC=4,CD=3,当△ECD绕点C顺时针旋转一周时,请直接写出BD长的取值范围.
13.(9分)【课本再现】
(1)我们知道,平移、轴对称和旋转都属于全等变换,如图1,是4×4正方形网格,A,D,C均是格点,点B,E分别在CD和AC上,∠ACB=90°,△ABC≌△DEC,请你判断△ABC是通过怎样的变换得到△DEC的 填: .
【深入探究】
(2)在图1中,AB与网格线的交点用F表示,连接CF,如图2,探究CF与DE的关系.
【拓展延伸】
(3)将图2中的点B,E绕着点C同时顺时针旋转相同的角度得到点B',E',连接AB',DE',作AB'的中点F',连接CF',如图3,猜想CF'与DE'的关系,并进行证明.
参考答案
1.A 2.B 3.C 4.C 5.C
6.A 【解析】如图,连接BD,交AC于点O.
∵四边形ABCD是菱形,
∴CD=AB=2,∠BCD=∠BAD=60°,∠ACD=∠BAC=∠BAD=30°,OA=OC,AC⊥BD,
∴OB=AB=1,
∴OA=OB=,
∴AC=2.
由旋转的性质得AE=AB=2,∠EAG=∠BAD=60°,
∴CE=AC-AE=2-2.
∵四边形AEFG是菱形,
∴EF∥AG,
∴∠CEP=∠EAG=60°,
∴∠CEP+∠ACD=90°,
∴∠CPE=90°,
∴PE=CE=-1,PC=PE=3-,
∴DP=CD-PC=2-(3-)=-1.
故选A.
7.图形①绕D点顺时针旋转90°,并向下平移3个单位长度得到图形②
8.(-2,15)
9.(1,1)或(4,4) 【解析】如图,分两种情形,旋转中心分别为(1,1)或(4,4).
故答案为(1,1)或(4,4).
10.【解析】(1)(-3,-2).
(2)如图,△A1OB1即所求作,点B1的坐标(3,-1).
(3)如图,点P即所求作,最小值AB'=B'P+PA==.
11.【解析】(1)证明:∵将△ADF绕点A顺时针旋转90°得到△ABQ,
∴△ADF≌△ABQ,∴AQ=AF,∠BAQ=∠DAF.
∵∠EAF=45°,∴∠DAF+∠BAE=45°,
∴∠QAE=45°,∴∠QAE=∠FAE.
在△AQE和△AFE中,
∴△AQE≌△AFE,∴∠AEQ=∠AEF,
∴EA是∠QED的平分线.
(2)∵四边形ABCD是正方形,∴∠ADB=∠ABD=45°.
由旋转的性质,易知QB=DF,∠ABQ=∠ADB=45°,
∴∠QBE=∠ABQ+∠ABD=90°.
由(1)知△AQE≌△AFE,∴QE=EF.
在Rt△QBE中,QB2+BE2=QE2,
∴EF2=BE2+DF2=1+9=10,∴EF=.
12.【解析】(1)∵△ABC是等边三角形,∴AC=BC,∠BAC=∠ACB=60°.
∵△ECD是等边三角形,
∴CE=CD,∠DCE=60°,
∴∠ACB=∠DCE=60°,
∴∠ACB+∠BCE=∠DCE+∠BCE,
即∠ACE=∠BCD.
在△ACE和△BCD中,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠CAE=∠CBD,
在△ABF中,∠AFB=180°-(∠BAF+∠ABF)
=180°-(∠BAF+∠CBF+∠ABC)
=180°-(∠BAC+∠ABC)
=180°-(60°+60°)=60°,
∴∠AFB=60°.
故答案为60°;AE=BD.
(2)(1)中结论仍成立.
证明:∵△ABC是等边三角形,
∴AC=BC,∠BAC=∠ACB=60°.
∵△ECD是等边三角形,
∴CE=CD,∠DCE=60°,
∴∠ACB=∠DCE=60°,
∴∠ACB+∠BCE=∠DCE+∠BCE,
即∠ACE=∠BCD.
在△ACE和△BCD中,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠CAE=∠CBD.
∵∠AFB+∠CBD=∠ACB+∠CAE,
∴∠AFB=∠ACB.
∵∠ACB=60°,∴∠AFB=60°.
(3)BD长的取值范围为1≤BD≤7.
提示:在△BCD中,BC+CD>BD,BC-CD∴点D在BC的延长线上时,BD最大,最大为4+3=7,
当点D在线段BC上时,BD最小,最小为4-3=1,
∴1≤BD≤7.
13.【解析】(1)轴对称.
(2)CF⊥DE,DE=2CF.理由如下.
∵F是AB的中点,∠ACB=90°,
∴CF=AB=BF,∠BAC+∠ABC=90°,
∴∠ABC=∠FCB.
又∵△ABC≌△DEC,
∴AB=DE,∠BAC=∠CDE,
∴DE=2CF,∠CDE+∠FCB=90°,
∴CF⊥DE.
(3)CF'⊥DE',DE'=2CF'.理由如下:
延长CF'并截取F'M=CF',连接AM,延长F'C交DE'于点N,连接CB',CE'.
∵点B,E绕着点C同时顺时针旋转相同的角度得到点B',E',
∴CB=CB',CE=CE',∠BCB'=∠ECE',
∴∠BCE=∠B'CE'=90°.
∴∠DCE'+∠ACB'=180°.
∵△ABC≌△DEC,
∴CE=CB,
∴CB'=CE'.
∵F'为AB'的中点,
∴AF'=B'F'.
又∵∠AF'M=∠CF'B'
∴△AF'M≌△B'F'C,
∴∠M=∠B'CM,
∴AM∥CB',
∴∠MAC+∠ACB'=180°,
∴∠MAC=∠DCE'.
∵△ABC≌△DEC,
∴AC=DC.
∴△AMC≌△CE'D.
∴CM=DE',∠ACM=∠CDE',
∵CM=2CF',∠ACB=90°,
∴DE'=2CF',∠ACM+∠DCN=90°,
∴∠CDE'+∠DCN=90°,
∴∠DNC=90°,
∴CF'⊥DE'.
2
(建议用时:80分钟 分值:60分)
一、选择题(本大题共6小题,每小题3分,满分18分)
1.下列图案是我国部分博物馆标志,其中既是轴对称图形又是中心对称图形的是 ( )
A B C D
2.如图,五角星的五个顶点等分圆周,把这个图形绕着圆心顺时针旋转一定的角度后能与自身重合,那么这个角度至少为 ( )
A.60° B.72° C.75° D.90°
3.下列现象中:①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.属于旋转的有 ( )
A.2个 B.3个 C.4个 D.5个
4.点P(2a+1,4)与P'(1,3b-1)关于原点对称,则2a+b的值为 ( )
A.3 B.-2 C.-3 D.2
5.把点P(x,y)绕原点顺时针旋转270°,点P的对应点的坐标是 ( )
A.(y,-x) B.(-x,-y)
C.(-y,x) D.(x,y)
6.如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是 ( )
A.-1 B.-2
C.2 -1 D.2-2
二、填空题(本大题共3小题,每小题3分,满分9分)
7.如图,在方格纸中,图形②可以看作是图形①经过若干次图形变化(平移、轴对称、旋转)得到的,写出一种由图形①得到图形②的变化过程: .
8.若x2+bx+c=(x+5)(x-3),则P(b,c)关于原点对称点的坐标是 .
9.如图,点A、B、C、D分别在正方形网格的格点上,其中A点的坐标为(-1,5),B点的坐标为(3,3),小明发现,线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标是 .
三、解答题(本大题共4小题,满分33分)
10.(7分)在如图所示的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,2),B(1,3).
(1)点A关于点O中心对称的点的坐标为 .
(2)△AOB绕点O顺时针旋转90°后得到△A1OB1,在方格纸中画出△A1OB1,并写出点B1的坐标 .
(3)在y轴上找一点P,使得PA+PB最小,请在图中标出点P的位置,并求出这个最小值.
11.(8分)如图,在正方形ABCD中,E,F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°得到△ABQ,连接EQ.
(1)求证:EA是∠QED的平分线.
(2)已知BE=1,DF=3,求EF的长.
12.(9分)如图,△ABC和△ECD都是等边三角形,直线AE,BD交于点F.
(1)如图1,当A,C,D三点在同一直线上时,∠AFB的度数为 ,线段AE与BD的数量关系为 .
(2)如图2,当△ECD绕点C顺时针旋转α(0°≤α<360°)时,(1)中的结论是否还成立 若不成立,请说明理由;若成立,请就图2给予证明.
(3)若AC=4,CD=3,当△ECD绕点C顺时针旋转一周时,请直接写出BD长的取值范围.
13.(9分)【课本再现】
(1)我们知道,平移、轴对称和旋转都属于全等变换,如图1,是4×4正方形网格,A,D,C均是格点,点B,E分别在CD和AC上,∠ACB=90°,△ABC≌△DEC,请你判断△ABC是通过怎样的变换得到△DEC的 填: .
【深入探究】
(2)在图1中,AB与网格线的交点用F表示,连接CF,如图2,探究CF与DE的关系.
【拓展延伸】
(3)将图2中的点B,E绕着点C同时顺时针旋转相同的角度得到点B',E',连接AB',DE',作AB'的中点F',连接CF',如图3,猜想CF'与DE'的关系,并进行证明.
参考答案
1.A 2.B 3.C 4.C 5.C
6.A 【解析】如图,连接BD,交AC于点O.
∵四边形ABCD是菱形,
∴CD=AB=2,∠BCD=∠BAD=60°,∠ACD=∠BAC=∠BAD=30°,OA=OC,AC⊥BD,
∴OB=AB=1,
∴OA=OB=,
∴AC=2.
由旋转的性质得AE=AB=2,∠EAG=∠BAD=60°,
∴CE=AC-AE=2-2.
∵四边形AEFG是菱形,
∴EF∥AG,
∴∠CEP=∠EAG=60°,
∴∠CEP+∠ACD=90°,
∴∠CPE=90°,
∴PE=CE=-1,PC=PE=3-,
∴DP=CD-PC=2-(3-)=-1.
故选A.
7.图形①绕D点顺时针旋转90°,并向下平移3个单位长度得到图形②
8.(-2,15)
9.(1,1)或(4,4) 【解析】如图,分两种情形,旋转中心分别为(1,1)或(4,4).
故答案为(1,1)或(4,4).
10.【解析】(1)(-3,-2).
(2)如图,△A1OB1即所求作,点B1的坐标(3,-1).
(3)如图,点P即所求作,最小值AB'=B'P+PA==.
11.【解析】(1)证明:∵将△ADF绕点A顺时针旋转90°得到△ABQ,
∴△ADF≌△ABQ,∴AQ=AF,∠BAQ=∠DAF.
∵∠EAF=45°,∴∠DAF+∠BAE=45°,
∴∠QAE=45°,∴∠QAE=∠FAE.
在△AQE和△AFE中,
∴△AQE≌△AFE,∴∠AEQ=∠AEF,
∴EA是∠QED的平分线.
(2)∵四边形ABCD是正方形,∴∠ADB=∠ABD=45°.
由旋转的性质,易知QB=DF,∠ABQ=∠ADB=45°,
∴∠QBE=∠ABQ+∠ABD=90°.
由(1)知△AQE≌△AFE,∴QE=EF.
在Rt△QBE中,QB2+BE2=QE2,
∴EF2=BE2+DF2=1+9=10,∴EF=.
12.【解析】(1)∵△ABC是等边三角形,∴AC=BC,∠BAC=∠ACB=60°.
∵△ECD是等边三角形,
∴CE=CD,∠DCE=60°,
∴∠ACB=∠DCE=60°,
∴∠ACB+∠BCE=∠DCE+∠BCE,
即∠ACE=∠BCD.
在△ACE和△BCD中,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠CAE=∠CBD,
在△ABF中,∠AFB=180°-(∠BAF+∠ABF)
=180°-(∠BAF+∠CBF+∠ABC)
=180°-(∠BAC+∠ABC)
=180°-(60°+60°)=60°,
∴∠AFB=60°.
故答案为60°;AE=BD.
(2)(1)中结论仍成立.
证明:∵△ABC是等边三角形,
∴AC=BC,∠BAC=∠ACB=60°.
∵△ECD是等边三角形,
∴CE=CD,∠DCE=60°,
∴∠ACB=∠DCE=60°,
∴∠ACB+∠BCE=∠DCE+∠BCE,
即∠ACE=∠BCD.
在△ACE和△BCD中,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠CAE=∠CBD.
∵∠AFB+∠CBD=∠ACB+∠CAE,
∴∠AFB=∠ACB.
∵∠ACB=60°,∴∠AFB=60°.
(3)BD长的取值范围为1≤BD≤7.
提示:在△BCD中,BC+CD>BD,BC-CD
当点D在线段BC上时,BD最小,最小为4-3=1,
∴1≤BD≤7.
13.【解析】(1)轴对称.
(2)CF⊥DE,DE=2CF.理由如下.
∵F是AB的中点,∠ACB=90°,
∴CF=AB=BF,∠BAC+∠ABC=90°,
∴∠ABC=∠FCB.
又∵△ABC≌△DEC,
∴AB=DE,∠BAC=∠CDE,
∴DE=2CF,∠CDE+∠FCB=90°,
∴CF⊥DE.
(3)CF'⊥DE',DE'=2CF'.理由如下:
延长CF'并截取F'M=CF',连接AM,延长F'C交DE'于点N,连接CB',CE'.
∵点B,E绕着点C同时顺时针旋转相同的角度得到点B',E',
∴CB=CB',CE=CE',∠BCB'=∠ECE',
∴∠BCE=∠B'CE'=90°.
∴∠DCE'+∠ACB'=180°.
∵△ABC≌△DEC,
∴CE=CB,
∴CB'=CE'.
∵F'为AB'的中点,
∴AF'=B'F'.
又∵∠AF'M=∠CF'B'
∴△AF'M≌△B'F'C,
∴∠M=∠B'CM,
∴AM∥CB',
∴∠MAC+∠ACB'=180°,
∴∠MAC=∠DCE'.
∵△ABC≌△DEC,
∴AC=DC.
∴△AMC≌△CE'D.
∴CM=DE',∠ACM=∠CDE',
∵CM=2CF',∠ACB=90°,
∴DE'=2CF',∠ACM+∠DCN=90°,
∴∠CDE'+∠DCN=90°,
∴∠DNC=90°,
∴CF'⊥DE'.
2
同课章节目录
