2023-2024学年数学人教版九年级上册第二十四章 圆 分层练习 (含答案)
文档属性
| 名称 | 2023-2024学年数学人教版九年级上册第二十四章 圆 分层练习 (含答案) | 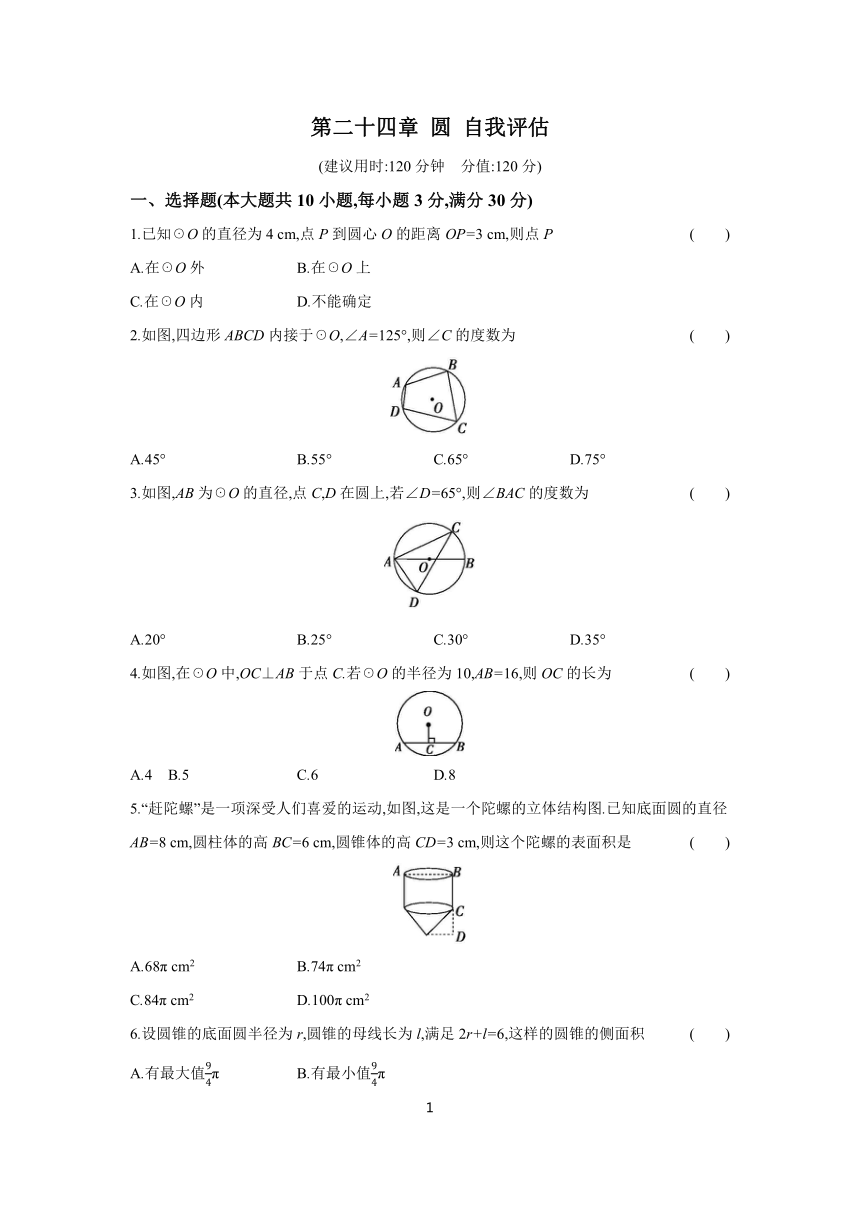 | |
| 格式 | docx | ||
| 文件大小 | 312.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 15:25:19 | ||
图片预览




文档简介
第二十四章 圆 自我评估
(建议用时:120分钟 分值:120分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.已知☉O的直径为4 cm,点P到圆心O的距离OP=3 cm,则点P ( )
A.在☉O外 B.在☉O上
C.在☉O内 D.不能确定
2.如图,四边形ABCD内接于☉O,∠A=125°,则∠C的度数为 ( )
A.45° B.55° C.65° D.75°
3.如图,AB为☉O的直径,点C,D在圆上,若∠D=65°,则∠BAC的度数为 ( )
A.20° B.25° C.30° D.35°
4.如图,在☉O中,OC⊥AB于点C.若☉O的半径为10,AB=16,则OC的长为 ( )
A.4 B.5 C.6 D.8
5.“赶陀螺”是一项深受人们喜爱的运动,如图,这是一个陀螺的立体结构图.已知底面圆的直径AB=8 cm,圆柱体的高BC=6 cm,圆锥体的高CD=3 cm,则这个陀螺的表面积是 ( )
A.68π cm2 B.74π cm2
C.84π cm2 D.100π cm2
6.设圆锥的底面圆半径为r,圆锥的母线长为l,满足2r+l=6,这样的圆锥的侧面积 ( )
A.有最大值π B.有最小值π
C.有最大值π D.有最小值π
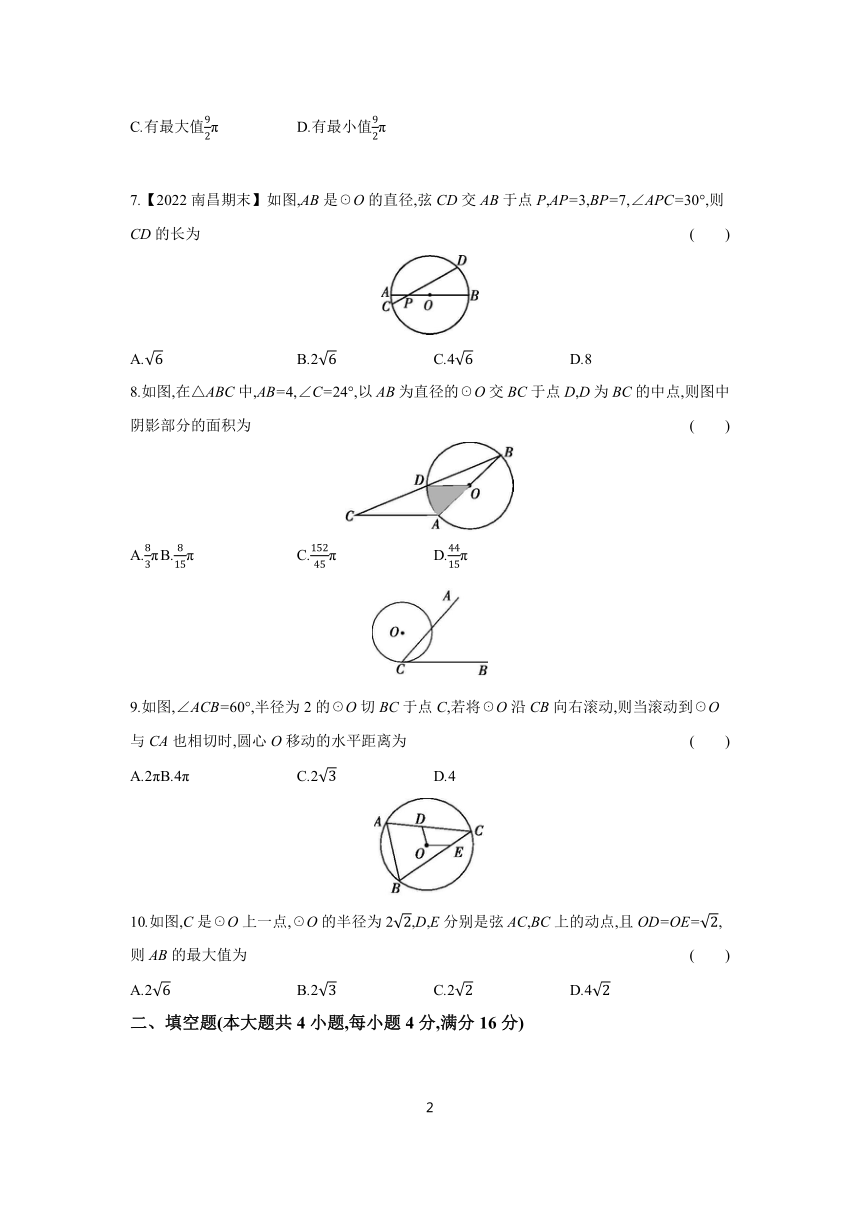
7.【2022南昌期末】如图,AB是☉O的直径,弦CD交AB于点P,AP=3,BP=7,∠APC=30°,则CD的长为 ( )
A. B.2 C.4 D.8
8.如图,在△ABC中,AB=4,∠C=24°,以AB为直径的☉O交BC于点D,D为BC的中点,则图中阴影部分的面积为 ( )
A.π B.π C.π D.π
9.如图,∠ACB=60°,半径为2的☉O切BC于点C,若将☉O沿CB向右滚动,则当滚动到☉O与CA也相切时,圆心O移动的水平距离为 ( )
A.2π B.4π C.2 D.4
10.如图,C是☉O上一点,☉O的半径为2,D,E分别是弦AC,BC上的动点,且OD=OE=,则AB的最大值为 ( )
A.2 B.2 C.2 D.4
二、填空题(本大题共4小题,每小题4分,满分16分)
11.如图,直线l是☉O的切线,A为切点,B为直线l上一点,连接OB交☉O于点C.若AB=12,OA=5,则BC的长为 .
12.数学活动课上,小东想测算一个圆形齿轮内圈圆的半径,如图所示,小东首先在内圈圆上取点A,B,再作弦AB的垂直平分线,垂足为C,交于点D,连接CD,经测量AB=8 cm,CD=2 cm,那么这个齿轮内圈圆的半径为 cm.
13.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,将Rt△ABC绕点C顺时针旋转,使斜边A'B'过B点,则线段CA扫过的面积为 .
14.如图,在Rt△ABC中,∠C=90°,△ABC的内切圆☉O与AB,BC,CA分别相切于点D,E,F,若☉O的半径为2,AD·DB=24,则AB的长为 .
三、解答题(本大题共8小题,满分74分)
15.(8分)在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何 ”用现代语言表述:如图,AB为☉O的直径,弦CD⊥AB于点E,AE=1寸,CD=10寸,求直径AB的长.
请你解答这个问题.
16.(8分)如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECD为平行四边形.
(2)连接CO,求证:CO平分∠BCE.
17.(8分)如图,PA,PB分别与☉O相切于点A,B,AC为☉O的弦,BC为☉O的直径,且∠P=60°,PB=2,连接AB.
(1)求证:△PAB是等边三角形.
(2)求AC的长.
18.(8分)如图,AB是☉O的直径,∠BAC=60°,P是OB上一点,过点P作AB的垂线,与AC的延长线交于点Q,过点C的切线CD交PQ于点D,连接OC.
(1)求证:△CDQ是等腰三角形.
(2)如果△CDQ≌△COB,求BP∶PO的值.
19.(8分)如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆☉O相交于点D,过点D作直线DG∥BC.
(1)若∠ACB=70°,则∠ADB= ;∠AEB= .
(2)求证:DE=CD.
(3)求证:DG是☉O的切线.
20.(10分)如图,直线AB经过☉O上的点C,直线AO与☉O交于点E和点D,OB与☉O交于点F,连接DF,DC.已知OA=OB,CA=CB,DE=10,DF=6.
(1)求证:①直线AB是☉O的切线;
②∠EDC=∠FDC.
(2)求CD的长.
21.(12分)先阅读材料,再解答问题:
小明同学在学习与圆有关的角时了解到:在同圆或等圆中,同弧(或等弧)所对的圆周角相等.如图1,A,B,C,D均为☉O上的点,则有∠C=∠D.小明还发现,若点E在☉O外,且与点D在直线AB同侧,则有∠D>∠E.
请你参考小明得出的结论,解答下列问题:
(1)如图2,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
①在图2中作出△ABC的外接圆(保留必要的作图痕迹,不写作法);
②若在x轴的正半轴上有一点D,且∠ACB=∠ADB,则点D的坐标为 .
(2)如图3,在平面直角坐标系xOy中,点A的坐标为(0,m),点B的坐标为(0,n),其中m>n>0.P为x轴正半轴上的一个动点,当∠APB达到最大时,求此时点P的坐标.
22.(12分)如图,△ACB内接于☉O,AB为直径,CD⊥AB于点D,E为☉O外一点,EO⊥AB,与BC交于点G,与☉O交于点F,连接EC,且EG=EC.
(1)求证:EC是☉O的切线.
(2)当∠ABC=22.5°时,连接CF.
①求证:AC=CF.
②若AD=1,求线段FG的长.
参考答案
1.A 2.B 3.B 4.C 5.C 6.C 7.C 8.B 9.C
10.A 11.8 12.5 13.8π 14.10
15.【解析】如图,连接OC.
∵弦CD⊥AB,AB为圆O的直径,
∴E为CD的中点.
又∵CD=10寸,
∴CE=DE=CD=5寸.
设OC=OA=x寸,则AB=2x寸,OE=(x-1)寸,
由勾股定理得OE2+CE2=OC2,
即(x-1)2+52=x2,
解得x=13,
∴AB=26寸.
故直径AB的长为26寸.
16.【解析】(1)由圆周角定理得∠B=∠E,又∵∠B=∠D,
∴∠E=∠D.
∵CE∥AD,
∴∠D+∠ECD=180°,
∴∠E+∠ECD=180°,
∴AE∥CD,
∴四边形AECD为平行四边形.
(2)如图,连接OE,OB.
∵四边形AECD为平行四边形,∴AD=CE.
又∵AD=BC,
∴CE=CB.
又∵OE=OB,OC=OC,
∴△EOC≌△BOC(SSS),∴∠ECO=∠BCO,
∴CO平分∠BCE.
17.【解析】(1)证明:∵PA,PB分别与☉O相切于点A,B,
∴PA=PB.
又∵∠P=60°,∴△PAB是等边三角形.
(2)由(1)知△PAB是等边三角形,
∴AB=PB=2,∠PBA=60°.
∵BC是☉O的直径,PB是☉O的切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,∴BC=2AC,
∴在Rt△ABC中,AC2+22=(2AC)2,
∴AC=.
18.【解析】(1)证明:由已知得∠ACB=90°,∠ABC=30°,
∴∠Q=30°,∠BCO=∠ABC=30°.
∵CD是☉O的切线,CO是半径,
∴CD⊥CO,
∴∠DCQ=∠BCO=30°,
∴∠DCQ=∠Q.
故△CDQ是等腰三角形.
(2)设☉O的半径为1,则AB=2,OC=1,BC=.
∵等腰三角形CDQ与等腰三角形COB全等,
∴CQ=BC=,
∴AQ=AC+CQ=1+,
∴AP=AQ=,
∴BP=AB-AP=,
∴PO=AP-AO=,
∴BP∶PO=.
19.【解析】(1)如图,连接OD,
∵=,
∴∠ACB=∠ADB=70°,
∴∠ABC+∠BAC=110°.
∵点E是△ABC的内心,
∴AE平分∠BAC,BE平分∠ABC,
∴∠BAE=∠CAE,∠ABE=∠CBE,
∴∠BAE+∠ABE=55°,
∴∠AEB=125°.
故答案为70°;125°.
(2)证明:∵∠BAE=∠CAE,
∴=,
∴BD=CD.
∵∠BAE=∠CAE=∠CBD,∠ABE=∠CBE,
∴∠BED=∠BAE+∠ABE=∠CBD+∠CBE=∠DBE,
∴BD=DE,
∴DE=CD.
(3)证明:∵=,
∴OD⊥BC.
∵DG∥BC,
∴OD⊥DG.
又∵OD是半径,
∴DG是☉O的切线.
20.【解析】(1)①证明:如图,连接OC.
∵OA=OB,AC=CB,
∴OC⊥AB.
∵点C在☉O上,
∴AB是☉O切线.
②证明:∵OA=OB,AC=CB,
∴∠AOC=∠BOC.
∵OD=OF,
∴∠ODF=∠OFD.
∵∠AOB=∠ODF+∠OFD=∠AOC+∠BOC,
∴∠BOC=∠OFD,
∴OC∥DF,
∴∠CDF=∠OCD.
∵OD=OC,
∴∠ODC=∠OCD,
∴∠ADC=∠CDF.
(2)如图,作ON⊥DF于点N,延长DF交AB于点M.
∵ON⊥DF,
∴DN=NF=3.
在Rt△ODN中,∠OND=90°,OD=5,DN=3,
∴ON==4.
∵∠OCM+∠CMN=180°,∠OCM=90°,
∴∠OCM=∠CMN=∠MNO=90°,
∴四边形OCMN是矩形,
∴ON=CM=4,MN=OC=5,
在Rt△CDM中,∠DMC=90°,CM=4,DM=DN+MN=8,
∴CD===4.
21.【解析】(1)①△ABC的外接圆如图1所示:
②根据图形可得点D的坐标是(7,0).
(2)当以AB为弦的圆与x轴正半轴相切于点P时,∠APB达到最大,如图2,过AB的中点D作CD⊥y轴,连接CP,CB.
∵A的坐标为(0,m),点B的坐标为(0,n),
∴点D的坐标是0,,即BC=PC=.
在Rt△BCD中,BC=,BD=,
则CD==,
则OP=CD=,
故点P的坐标是(,0).
22.【解析】
(1)证明:如图,连接OC.
∵OC=OB,∴∠OCB=∠B.
∵EG=EC,
∴∠ECG=∠EGC.
∵EO⊥AB,
∴∠OGB+∠B=90°.
∵∠EGC=∠OGB,∴∠OCB+∠ECG=∠B+∠OGB=90°,
∴OC⊥CE.
∵OC是☉O的半径,∴EC是☉O的切线.
(2)①证明:∵∠ABC=22.5°,∠OCB=∠B,
∴∠AOC=45°.
∵EO⊥AB,∴∠COF=45°,∴=,∴AC=CF.
②如图,过点C作CM⊥OE于点M.
∵AB为☉O的直径,∴∠ACB=90°.
∵∠ABC=22.5°,∠GOB=90°,
∴∠A=∠OGB=∠67.5°,∴∠FGC=67.5°.
∵∠COF=45°,OC=OF,∴∠OFC=∠OCF=67.5°,
∴∠GFC=∠FGC,∴CF=CG,∴FM=GM.
∵∠AOC=∠COF,CD⊥OA,CM⊥OF,∴CD=CM.
在Rt△ACD和Rt△FCM中,
∴Rt△ACD≌Rt△FCM,
∴FM=AD=1,∴FG=2FM=2.
2
(建议用时:120分钟 分值:120分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.已知☉O的直径为4 cm,点P到圆心O的距离OP=3 cm,则点P ( )
A.在☉O外 B.在☉O上
C.在☉O内 D.不能确定
2.如图,四边形ABCD内接于☉O,∠A=125°,则∠C的度数为 ( )
A.45° B.55° C.65° D.75°
3.如图,AB为☉O的直径,点C,D在圆上,若∠D=65°,则∠BAC的度数为 ( )
A.20° B.25° C.30° D.35°
4.如图,在☉O中,OC⊥AB于点C.若☉O的半径为10,AB=16,则OC的长为 ( )
A.4 B.5 C.6 D.8
5.“赶陀螺”是一项深受人们喜爱的运动,如图,这是一个陀螺的立体结构图.已知底面圆的直径AB=8 cm,圆柱体的高BC=6 cm,圆锥体的高CD=3 cm,则这个陀螺的表面积是 ( )
A.68π cm2 B.74π cm2
C.84π cm2 D.100π cm2
6.设圆锥的底面圆半径为r,圆锥的母线长为l,满足2r+l=6,这样的圆锥的侧面积 ( )
A.有最大值π B.有最小值π
C.有最大值π D.有最小值π
7.【2022南昌期末】如图,AB是☉O的直径,弦CD交AB于点P,AP=3,BP=7,∠APC=30°,则CD的长为 ( )
A. B.2 C.4 D.8
8.如图,在△ABC中,AB=4,∠C=24°,以AB为直径的☉O交BC于点D,D为BC的中点,则图中阴影部分的面积为 ( )
A.π B.π C.π D.π
9.如图,∠ACB=60°,半径为2的☉O切BC于点C,若将☉O沿CB向右滚动,则当滚动到☉O与CA也相切时,圆心O移动的水平距离为 ( )
A.2π B.4π C.2 D.4
10.如图,C是☉O上一点,☉O的半径为2,D,E分别是弦AC,BC上的动点,且OD=OE=,则AB的最大值为 ( )
A.2 B.2 C.2 D.4
二、填空题(本大题共4小题,每小题4分,满分16分)
11.如图,直线l是☉O的切线,A为切点,B为直线l上一点,连接OB交☉O于点C.若AB=12,OA=5,则BC的长为 .
12.数学活动课上,小东想测算一个圆形齿轮内圈圆的半径,如图所示,小东首先在内圈圆上取点A,B,再作弦AB的垂直平分线,垂足为C,交于点D,连接CD,经测量AB=8 cm,CD=2 cm,那么这个齿轮内圈圆的半径为 cm.
13.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,将Rt△ABC绕点C顺时针旋转,使斜边A'B'过B点,则线段CA扫过的面积为 .
14.如图,在Rt△ABC中,∠C=90°,△ABC的内切圆☉O与AB,BC,CA分别相切于点D,E,F,若☉O的半径为2,AD·DB=24,则AB的长为 .
三、解答题(本大题共8小题,满分74分)
15.(8分)在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何 ”用现代语言表述:如图,AB为☉O的直径,弦CD⊥AB于点E,AE=1寸,CD=10寸,求直径AB的长.
请你解答这个问题.
16.(8分)如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECD为平行四边形.
(2)连接CO,求证:CO平分∠BCE.
17.(8分)如图,PA,PB分别与☉O相切于点A,B,AC为☉O的弦,BC为☉O的直径,且∠P=60°,PB=2,连接AB.
(1)求证:△PAB是等边三角形.
(2)求AC的长.
18.(8分)如图,AB是☉O的直径,∠BAC=60°,P是OB上一点,过点P作AB的垂线,与AC的延长线交于点Q,过点C的切线CD交PQ于点D,连接OC.
(1)求证:△CDQ是等腰三角形.
(2)如果△CDQ≌△COB,求BP∶PO的值.
19.(8分)如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆☉O相交于点D,过点D作直线DG∥BC.
(1)若∠ACB=70°,则∠ADB= ;∠AEB= .
(2)求证:DE=CD.
(3)求证:DG是☉O的切线.
20.(10分)如图,直线AB经过☉O上的点C,直线AO与☉O交于点E和点D,OB与☉O交于点F,连接DF,DC.已知OA=OB,CA=CB,DE=10,DF=6.
(1)求证:①直线AB是☉O的切线;
②∠EDC=∠FDC.
(2)求CD的长.
21.(12分)先阅读材料,再解答问题:
小明同学在学习与圆有关的角时了解到:在同圆或等圆中,同弧(或等弧)所对的圆周角相等.如图1,A,B,C,D均为☉O上的点,则有∠C=∠D.小明还发现,若点E在☉O外,且与点D在直线AB同侧,则有∠D>∠E.
请你参考小明得出的结论,解答下列问题:
(1)如图2,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
①在图2中作出△ABC的外接圆(保留必要的作图痕迹,不写作法);
②若在x轴的正半轴上有一点D,且∠ACB=∠ADB,则点D的坐标为 .
(2)如图3,在平面直角坐标系xOy中,点A的坐标为(0,m),点B的坐标为(0,n),其中m>n>0.P为x轴正半轴上的一个动点,当∠APB达到最大时,求此时点P的坐标.
22.(12分)如图,△ACB内接于☉O,AB为直径,CD⊥AB于点D,E为☉O外一点,EO⊥AB,与BC交于点G,与☉O交于点F,连接EC,且EG=EC.
(1)求证:EC是☉O的切线.
(2)当∠ABC=22.5°时,连接CF.
①求证:AC=CF.
②若AD=1,求线段FG的长.
参考答案
1.A 2.B 3.B 4.C 5.C 6.C 7.C 8.B 9.C
10.A 11.8 12.5 13.8π 14.10
15.【解析】如图,连接OC.
∵弦CD⊥AB,AB为圆O的直径,
∴E为CD的中点.
又∵CD=10寸,
∴CE=DE=CD=5寸.
设OC=OA=x寸,则AB=2x寸,OE=(x-1)寸,
由勾股定理得OE2+CE2=OC2,
即(x-1)2+52=x2,
解得x=13,
∴AB=26寸.
故直径AB的长为26寸.
16.【解析】(1)由圆周角定理得∠B=∠E,又∵∠B=∠D,
∴∠E=∠D.
∵CE∥AD,
∴∠D+∠ECD=180°,
∴∠E+∠ECD=180°,
∴AE∥CD,
∴四边形AECD为平行四边形.
(2)如图,连接OE,OB.
∵四边形AECD为平行四边形,∴AD=CE.
又∵AD=BC,
∴CE=CB.
又∵OE=OB,OC=OC,
∴△EOC≌△BOC(SSS),∴∠ECO=∠BCO,
∴CO平分∠BCE.
17.【解析】(1)证明:∵PA,PB分别与☉O相切于点A,B,
∴PA=PB.
又∵∠P=60°,∴△PAB是等边三角形.
(2)由(1)知△PAB是等边三角形,
∴AB=PB=2,∠PBA=60°.
∵BC是☉O的直径,PB是☉O的切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,∴BC=2AC,
∴在Rt△ABC中,AC2+22=(2AC)2,
∴AC=.
18.【解析】(1)证明:由已知得∠ACB=90°,∠ABC=30°,
∴∠Q=30°,∠BCO=∠ABC=30°.
∵CD是☉O的切线,CO是半径,
∴CD⊥CO,
∴∠DCQ=∠BCO=30°,
∴∠DCQ=∠Q.
故△CDQ是等腰三角形.
(2)设☉O的半径为1,则AB=2,OC=1,BC=.
∵等腰三角形CDQ与等腰三角形COB全等,
∴CQ=BC=,
∴AQ=AC+CQ=1+,
∴AP=AQ=,
∴BP=AB-AP=,
∴PO=AP-AO=,
∴BP∶PO=.
19.【解析】(1)如图,连接OD,
∵=,
∴∠ACB=∠ADB=70°,
∴∠ABC+∠BAC=110°.
∵点E是△ABC的内心,
∴AE平分∠BAC,BE平分∠ABC,
∴∠BAE=∠CAE,∠ABE=∠CBE,
∴∠BAE+∠ABE=55°,
∴∠AEB=125°.
故答案为70°;125°.
(2)证明:∵∠BAE=∠CAE,
∴=,
∴BD=CD.
∵∠BAE=∠CAE=∠CBD,∠ABE=∠CBE,
∴∠BED=∠BAE+∠ABE=∠CBD+∠CBE=∠DBE,
∴BD=DE,
∴DE=CD.
(3)证明:∵=,
∴OD⊥BC.
∵DG∥BC,
∴OD⊥DG.
又∵OD是半径,
∴DG是☉O的切线.
20.【解析】(1)①证明:如图,连接OC.
∵OA=OB,AC=CB,
∴OC⊥AB.
∵点C在☉O上,
∴AB是☉O切线.
②证明:∵OA=OB,AC=CB,
∴∠AOC=∠BOC.
∵OD=OF,
∴∠ODF=∠OFD.
∵∠AOB=∠ODF+∠OFD=∠AOC+∠BOC,
∴∠BOC=∠OFD,
∴OC∥DF,
∴∠CDF=∠OCD.
∵OD=OC,
∴∠ODC=∠OCD,
∴∠ADC=∠CDF.
(2)如图,作ON⊥DF于点N,延长DF交AB于点M.
∵ON⊥DF,
∴DN=NF=3.
在Rt△ODN中,∠OND=90°,OD=5,DN=3,
∴ON==4.
∵∠OCM+∠CMN=180°,∠OCM=90°,
∴∠OCM=∠CMN=∠MNO=90°,
∴四边形OCMN是矩形,
∴ON=CM=4,MN=OC=5,
在Rt△CDM中,∠DMC=90°,CM=4,DM=DN+MN=8,
∴CD===4.
21.【解析】(1)①△ABC的外接圆如图1所示:
②根据图形可得点D的坐标是(7,0).
(2)当以AB为弦的圆与x轴正半轴相切于点P时,∠APB达到最大,如图2,过AB的中点D作CD⊥y轴,连接CP,CB.
∵A的坐标为(0,m),点B的坐标为(0,n),
∴点D的坐标是0,,即BC=PC=.
在Rt△BCD中,BC=,BD=,
则CD==,
则OP=CD=,
故点P的坐标是(,0).
22.【解析】
(1)证明:如图,连接OC.
∵OC=OB,∴∠OCB=∠B.
∵EG=EC,
∴∠ECG=∠EGC.
∵EO⊥AB,
∴∠OGB+∠B=90°.
∵∠EGC=∠OGB,∴∠OCB+∠ECG=∠B+∠OGB=90°,
∴OC⊥CE.
∵OC是☉O的半径,∴EC是☉O的切线.
(2)①证明:∵∠ABC=22.5°,∠OCB=∠B,
∴∠AOC=45°.
∵EO⊥AB,∴∠COF=45°,∴=,∴AC=CF.
②如图,过点C作CM⊥OE于点M.
∵AB为☉O的直径,∴∠ACB=90°.
∵∠ABC=22.5°,∠GOB=90°,
∴∠A=∠OGB=∠67.5°,∴∠FGC=67.5°.
∵∠COF=45°,OC=OF,∴∠OFC=∠OCF=67.5°,
∴∠GFC=∠FGC,∴CF=CG,∴FM=GM.
∵∠AOC=∠COF,CD⊥OA,CM⊥OF,∴CD=CM.
在Rt△ACD和Rt△FCM中,
∴Rt△ACD≌Rt△FCM,
∴FM=AD=1,∴FG=2FM=2.
2
同课章节目录
