2023-2024学年数学人教版九年级下册26.1.2 课时1 反比例函数的图象和性质(1) 分层练习 (含答案)
文档属性
| 名称 | 2023-2024学年数学人教版九年级下册26.1.2 课时1 反比例函数的图象和性质(1) 分层练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 150.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 15:37:33 | ||
图片预览


文档简介
26.1.2 课时1 反比例函数的图象和性质(1)
【练基础】
必备知识1 反比例函数的图象
1.【石家庄期末】已知函数y=(a+3)xa+1是反比例函数,则此反比例函数的图象在 ( )
A.第一、第三象限 B.第二、第四象限
C.第一、第四象限 D.第二、第三象限
2.点(3,-4)在反比例函数y=的图象上,则在此图象上的是点 ( )
A.(3,4) B.(-2,-6)
C.(-2,6) D.(-3,-4)
必备知识2 反比例函数的性质
3.下列四个函数中:①y=5x;②y=-5x;③y=;④y=-.当x>0时,y随x的增大而减小的函数有 ( )
A.0个 B.1个
C.2个 D.3个
4.反比例函数y=-(x>0)的图象位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.已知反比例函数y=,则下列描述不正确的是 ( )
A.图象位于第一、第三象限
B.图象必经过点4,
C.图象不可能与坐标轴相交
D.y随x的增大而减小
6.【石家庄月考】若点A(x1,-5),B(x2,2),C(x3,5)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是 ( )
A.x2C.x17.已知反比例函数y=的图象过点(-3,-12),且双曲线y=位于第二、第四象限,求m的值.
8.已知点A(m,2)、B(2,n)都在反比例函数y=的图象上.
(1)求m、n的值.
(2)若直线y=mx-n与x轴交于点C,求点C关于y轴对称点C'的坐标.
【练能力】
9.如图,在平面直角坐标系中有一矩形ABCD灰色区域,其中AB=1,AD=4,点C(2,1),有一动态扫描线为双曲线y=(x>0),当扫描线遇到灰色区域时,区域便由灰变亮,则下列能够使灰色区域变亮的k的值不可能是 ( )
A.k=1 B.k=2.2
C.k= D.k=4
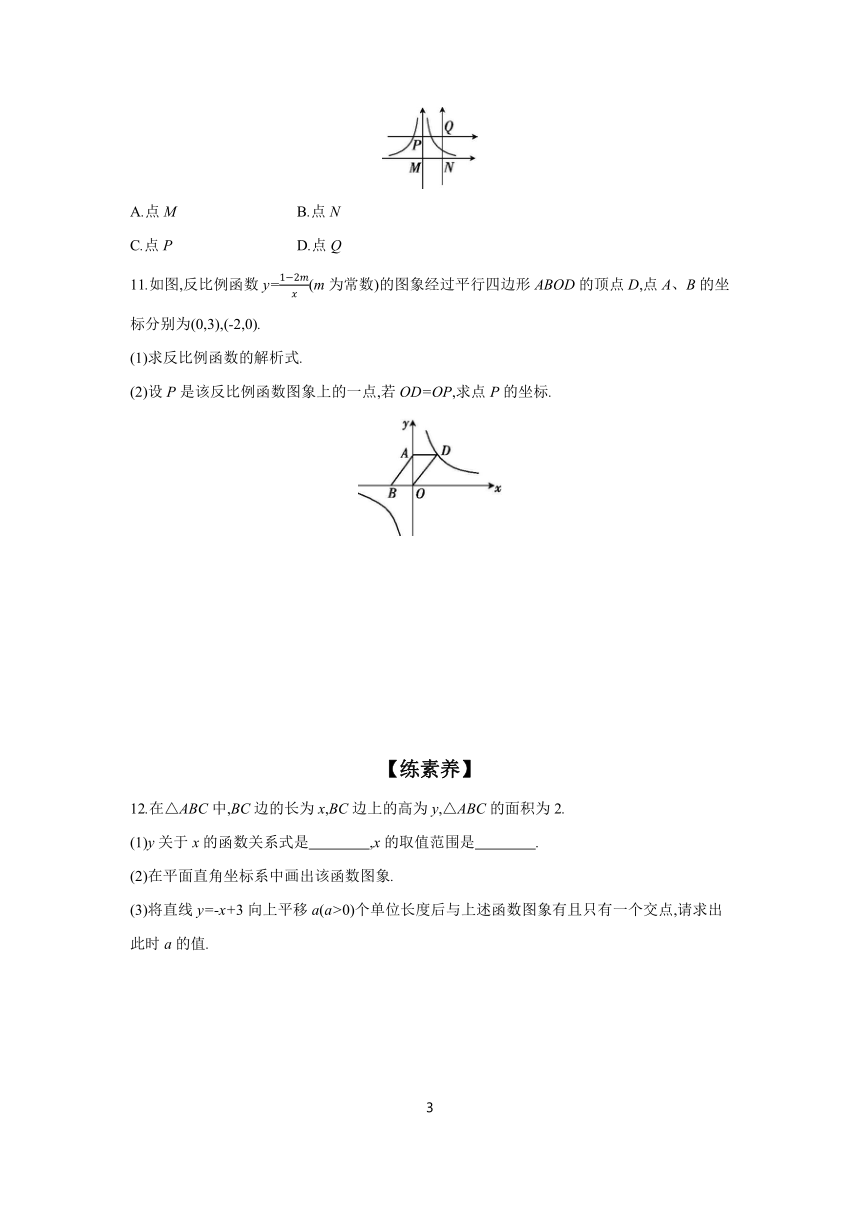
10.【2019·河北中考】如图,函数y=的图象所在坐标系的原点是 ( )
A.点M B.点N
C.点P D.点Q
11.如图,反比例函数y=(m为常数)的图象经过平行四边形ABOD的顶点D,点A、B的坐标分别为(0,3),(-2,0).
(1)求反比例函数的解析式.
(2)设P是该反比例函数图象上的一点,若OD=OP,求点P的坐标.
【练素养】
12.在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2.
(1)y关于x的函数关系式是 ,x的取值范围是 .
(2)在平面直角坐标系中画出该函数图象.
(3)将直线y=-x+3向上平移a(a>0)个单位长度后与上述函数图象有且只有一个交点,请求出此时a的值.
参考答案
练基础
1.A 2.C 3.C 4.D 5.D 6.B
7.【解析】根据点在图象上的含义,只要将(-3,-12)代入y=中,得-12=,
∴m=±6.
又∵双曲线y=位于第二、第四象限,
∴m<0,∴m=-6.
8.【解析】(1)将点A(m,2)、B(2,n)的坐标代入y=,
得2=,解得m=3,n===3,
所以m=n=3.
(2)直线为y=3x-3,
令y=0,x=1,
所以该直线与x轴的交点坐标为C(1,0),
点C关于y轴对称点C'的坐标为(-1,0).
练能力
9.A 10.A
11.【解析】(1)∵四边形ABOC为平行四边形,
∴AD∥OB,AD=OB=2,
而点A坐标为(0,3),∴点D坐标为(2,3),
∴1-2m=2×3=6,m=-,
∴反比例函数解析式为y=.
(2)∵反比例函数y=的图象关于原点中心对称,
∴当点P与点D关于原点对称,则OD=OP,此时点P坐标为(-2,-3).
∵反比例函数y=的图象关于直线y=x对称,
∴点P与点D(2,3)关于直线y=x对称时满足OP=OD,此时点P坐标为(3,2),
点(3,2)关于原点的对称点也满足OP=OD,此时点P坐标为(-3,-2).
综上所述,点P的坐标为(-2,-3),(3,2),(-3,-2).
练素养
12.【解析】(1)∵在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2,
∴xy=2,
∴xy=4,
∴y关于x的函数关系式是y=,
x的取值范围为x>0,
故答案为y=;x>0.
(2)在平面直角坐标系中画出该函数图象如图所示.
(3)将直线y=-x+3向上平移a(a>0)个单位长度后解析式为y=-x+3+a,
解整理得,x2-(3+a)x+4=0,
∵平移后的直线与上述函数图象有且只有一个交点.
∴Δ=(3+a)2-16=0,
解得a=1,a=-7(不合题意舍去),
故此时a的值为1.
2
【练基础】
必备知识1 反比例函数的图象
1.【石家庄期末】已知函数y=(a+3)xa+1是反比例函数,则此反比例函数的图象在 ( )
A.第一、第三象限 B.第二、第四象限
C.第一、第四象限 D.第二、第三象限
2.点(3,-4)在反比例函数y=的图象上,则在此图象上的是点 ( )
A.(3,4) B.(-2,-6)
C.(-2,6) D.(-3,-4)
必备知识2 反比例函数的性质
3.下列四个函数中:①y=5x;②y=-5x;③y=;④y=-.当x>0时,y随x的增大而减小的函数有 ( )
A.0个 B.1个
C.2个 D.3个
4.反比例函数y=-(x>0)的图象位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.已知反比例函数y=,则下列描述不正确的是 ( )
A.图象位于第一、第三象限
B.图象必经过点4,
C.图象不可能与坐标轴相交
D.y随x的增大而减小
6.【石家庄月考】若点A(x1,-5),B(x2,2),C(x3,5)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是 ( )
A.x2
8.已知点A(m,2)、B(2,n)都在反比例函数y=的图象上.
(1)求m、n的值.
(2)若直线y=mx-n与x轴交于点C,求点C关于y轴对称点C'的坐标.
【练能力】
9.如图,在平面直角坐标系中有一矩形ABCD灰色区域,其中AB=1,AD=4,点C(2,1),有一动态扫描线为双曲线y=(x>0),当扫描线遇到灰色区域时,区域便由灰变亮,则下列能够使灰色区域变亮的k的值不可能是 ( )
A.k=1 B.k=2.2
C.k= D.k=4
10.【2019·河北中考】如图,函数y=的图象所在坐标系的原点是 ( )
A.点M B.点N
C.点P D.点Q
11.如图,反比例函数y=(m为常数)的图象经过平行四边形ABOD的顶点D,点A、B的坐标分别为(0,3),(-2,0).
(1)求反比例函数的解析式.
(2)设P是该反比例函数图象上的一点,若OD=OP,求点P的坐标.
【练素养】
12.在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2.
(1)y关于x的函数关系式是 ,x的取值范围是 .
(2)在平面直角坐标系中画出该函数图象.
(3)将直线y=-x+3向上平移a(a>0)个单位长度后与上述函数图象有且只有一个交点,请求出此时a的值.
参考答案
练基础
1.A 2.C 3.C 4.D 5.D 6.B
7.【解析】根据点在图象上的含义,只要将(-3,-12)代入y=中,得-12=,
∴m=±6.
又∵双曲线y=位于第二、第四象限,
∴m<0,∴m=-6.
8.【解析】(1)将点A(m,2)、B(2,n)的坐标代入y=,
得2=,解得m=3,n===3,
所以m=n=3.
(2)直线为y=3x-3,
令y=0,x=1,
所以该直线与x轴的交点坐标为C(1,0),
点C关于y轴对称点C'的坐标为(-1,0).
练能力
9.A 10.A
11.【解析】(1)∵四边形ABOC为平行四边形,
∴AD∥OB,AD=OB=2,
而点A坐标为(0,3),∴点D坐标为(2,3),
∴1-2m=2×3=6,m=-,
∴反比例函数解析式为y=.
(2)∵反比例函数y=的图象关于原点中心对称,
∴当点P与点D关于原点对称,则OD=OP,此时点P坐标为(-2,-3).
∵反比例函数y=的图象关于直线y=x对称,
∴点P与点D(2,3)关于直线y=x对称时满足OP=OD,此时点P坐标为(3,2),
点(3,2)关于原点的对称点也满足OP=OD,此时点P坐标为(-3,-2).
综上所述,点P的坐标为(-2,-3),(3,2),(-3,-2).
练素养
12.【解析】(1)∵在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2,
∴xy=2,
∴xy=4,
∴y关于x的函数关系式是y=,
x的取值范围为x>0,
故答案为y=;x>0.
(2)在平面直角坐标系中画出该函数图象如图所示.
(3)将直线y=-x+3向上平移a(a>0)个单位长度后解析式为y=-x+3+a,
解整理得,x2-(3+a)x+4=0,
∵平移后的直线与上述函数图象有且只有一个交点.
∴Δ=(3+a)2-16=0,
解得a=1,a=-7(不合题意舍去),
故此时a的值为1.
2
