2023-2024学年数学人教版九年级下册26.1.2 课时2 反比例函数的图象和性质(2) 分层练习(含答案)
文档属性
| 名称 | 2023-2024学年数学人教版九年级下册26.1.2 课时2 反比例函数的图象和性质(2) 分层练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 142.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 15:38:09 | ||
图片预览

文档简介
26.1.2 课时2 反比例函数的图象和性质(2)
【练基础】
必备知识1 反比例函数增减性的应用
1.若点A(-1,y1),B(2,y2),C(3,y3)在反比例函数y=-的图象上,则y1,y2,y3的大小关系是 ( )
A.y1>y2>y3 B.y2>y3>y1
C.y1>y3>y2 D.y3>y2>y1
2.已知点A(a,y1),B(a+1,y2)在反比例函数y=(a是常数)的图象上,且y1A.a<0 B.a>0
C.0必备知识2 反比例函数与几何、一次函数、二次函数的结合
3.如图,正方形ABCD的两个顶点B,D在反比例函数y=的图象上,对角线AC,BD的交点恰好是坐标原点O,已知B(-1,1),则k的值是 ( )
A.-5 B.-4 C.-3 D.-1
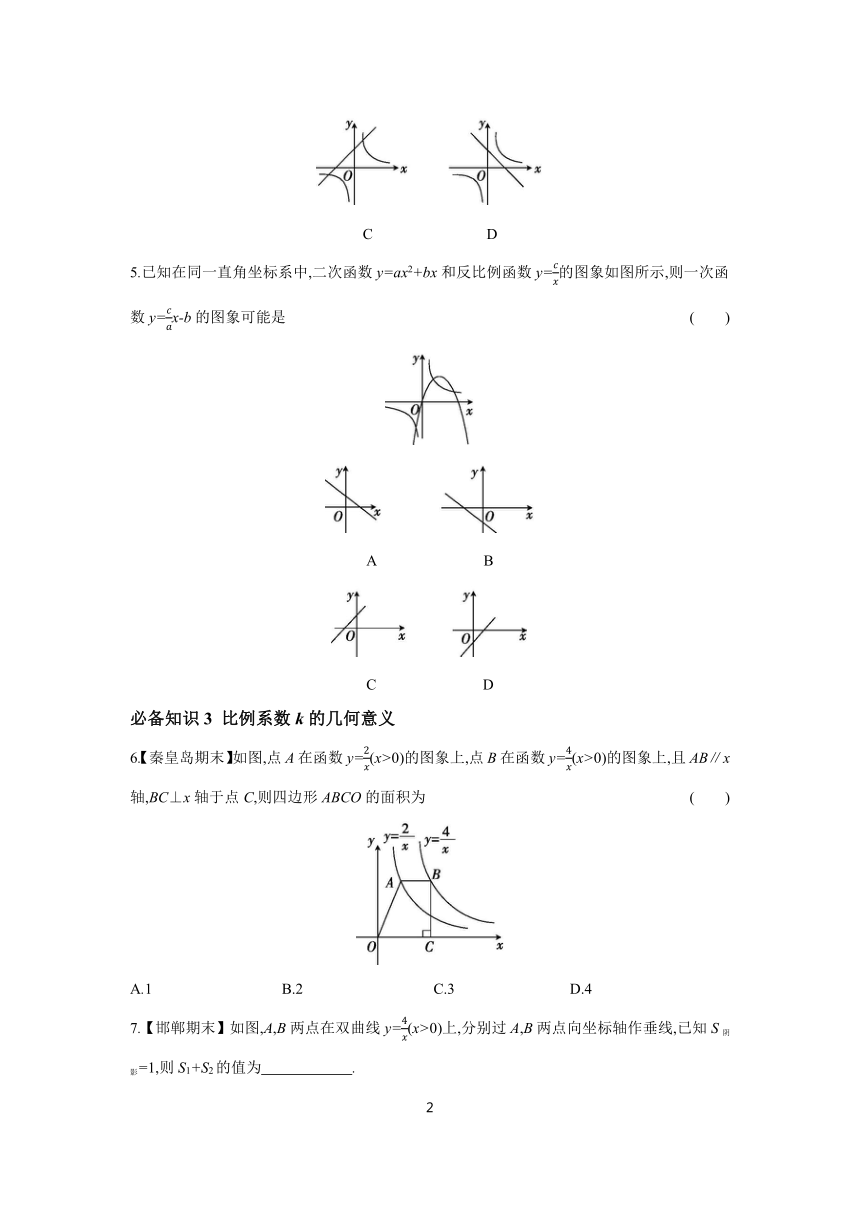
4.【唐山期末】在同一直角坐标系中,反比例函数y=与一次函数y=x+a(a≠0)的图象大致是 ( )
A B
C D
5.已知在同一直角坐标系中,二次函数y=ax2+bx和反比例函数y=的图象如图所示,则一次函数y=x-b的图象可能是 ( )
A B
C D
必备知识3 比例系数k的几何意义
6.【秦皇岛期末】如图,点A在函数y=(x>0)的图象上,点B在函数y=(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为 ( )
A.1 B.2 C.3 D.4
7.【邯郸期末】如图,A,B两点在双曲线y=(x>0)上,分别过A,B两点向坐标轴作垂线,已知S阴影=1,则S1+S2的值为 .
8.点P,Q,R在反比例函数y=(常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3.若OE=ED=DC,S1+S3=27,则S2的值为 .
【练能力】
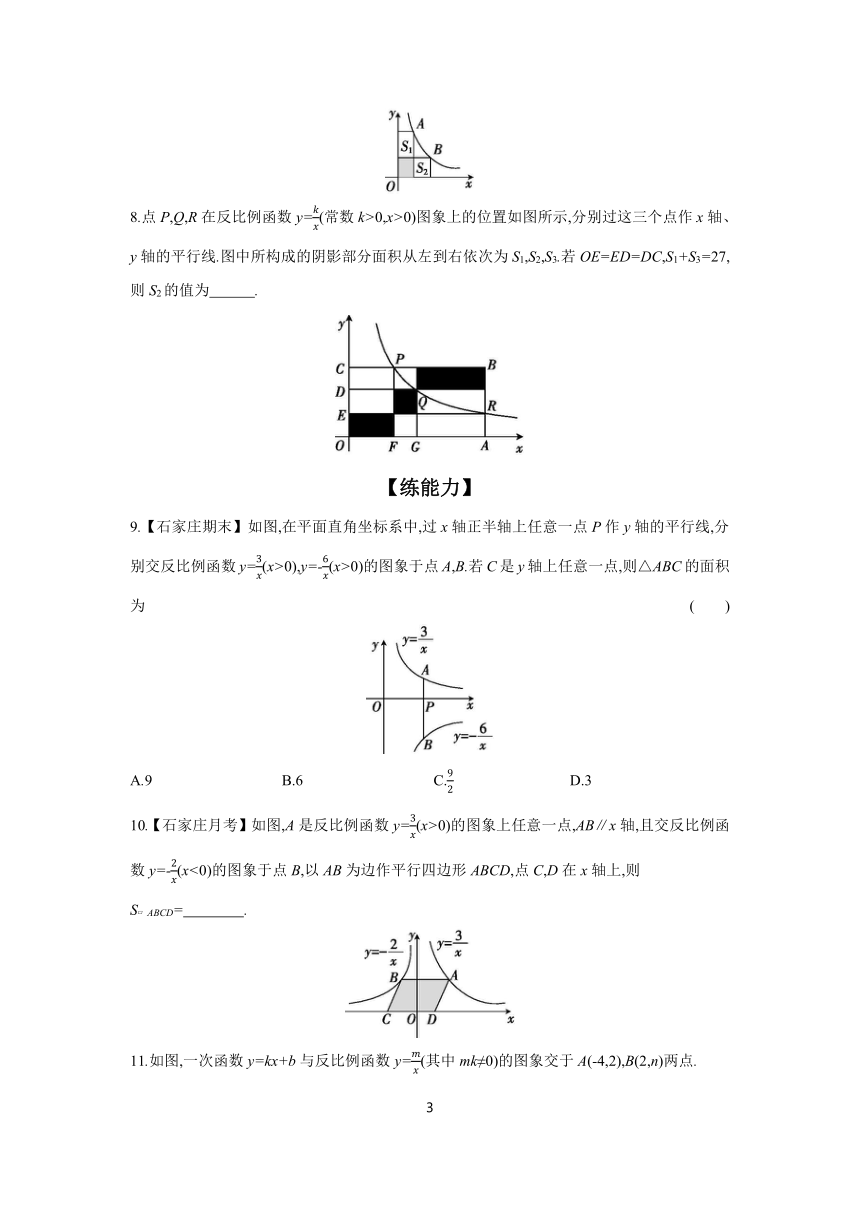
9.【石家庄期末】如图,在平面直角坐标系中,过x轴正半轴上任意一点P作y轴的平行线,分别交反比例函数y=(x>0),y=-(x>0)的图象于点A,B.若C是y轴上任意一点,则△ABC的面积为 ( )
A.9 B.6 C. D.3
10.【石家庄月考】如图,A是反比例函数y=(x>0)的图象上任意一点,AB∥x轴,且交反比例函数y=-(x<0)的图象于点B,以AB为边作平行四边形ABCD,点C,D在x轴上,则S ABCD= .
11.如图,一次函数y=kx+b与反比例函数y=(其中mk≠0)的图象交于A(-4,2),B(2,n)两点.
(1)求一次函数和反比例函数的表达式.
(2)求△ABO的面积.
(3)请直接写出当一次函数值大于反比例函数值时x的取值范围.
【练素养】
12.【2020·江西中考】如图,在Rt△ABC中,∠ACB=90°,顶点A,B都在反比例函数y=(x>0)的图象上,直线AC⊥x轴,垂足为D,连接OA,OC,并延长OC交AB于点E,当AB=2OA时,E恰好为AB的中点,若∠AOD=45°,OA=2.
(1)求反比例函数的解析式.
(2)求∠EOD的度数.
参考答案
练基础
1.C 2.D 3.D 4.C 5.B 6.C 7.6 8. 9.C
10.5
11.【解析】(1)∵一次函数y=kx+b与反比例函数y=(mk≠0)的图象交于A(-4,2),B(2,n)两点,
∴m=-8,n=-4,
∴ 解得
∴一次函数的表达式为y=-x-2,
反比例函数的表达式为y=-.
(2)设直线AB交y轴于点C.
在y=-x-2中,令x=0,则y=-2.
∴OC=2,
∴S△ABO=S△AOC+S△BOC=×2×4+×2×2=6.
(3)x<-4或012.【解析】(1)∵直线AC⊥x轴,垂足为D,∠AOD=45°,
∴△AOD是等腰直角三角形.
∵OA=2,
∴OD=AD=2,
∴A(2,2).
∵顶点A在反比例函数y=(x>0)的图象上,
∴k=2×2=4,
∴反比例函数的解析式为y=(x>0).
(2)∵AB=2OA,E恰好为AB的中点,
∴OA=AE.
∵在Rt△ABC中,∠ACB=90°,
∴CE=AE=BE,
∴∠AOE=∠AEO,∠ECB=∠EBC.
∵∠AEO=∠ECB+∠EBC=2∠EBC,
又∵BC∥x轴,
∴∠EOD=∠ECB,
∴∠AOE=2∠EOD.
∵∠AOD=45°,
∴∠EOD=15°.
2
【练基础】
必备知识1 反比例函数增减性的应用
1.若点A(-1,y1),B(2,y2),C(3,y3)在反比例函数y=-的图象上,则y1,y2,y3的大小关系是 ( )
A.y1>y2>y3 B.y2>y3>y1
C.y1>y3>y2 D.y3>y2>y1
2.已知点A(a,y1),B(a+1,y2)在反比例函数y=(a是常数)的图象上,且y1
C.0
3.如图,正方形ABCD的两个顶点B,D在反比例函数y=的图象上,对角线AC,BD的交点恰好是坐标原点O,已知B(-1,1),则k的值是 ( )
A.-5 B.-4 C.-3 D.-1
4.【唐山期末】在同一直角坐标系中,反比例函数y=与一次函数y=x+a(a≠0)的图象大致是 ( )
A B
C D
5.已知在同一直角坐标系中,二次函数y=ax2+bx和反比例函数y=的图象如图所示,则一次函数y=x-b的图象可能是 ( )
A B
C D
必备知识3 比例系数k的几何意义
6.【秦皇岛期末】如图,点A在函数y=(x>0)的图象上,点B在函数y=(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为 ( )
A.1 B.2 C.3 D.4
7.【邯郸期末】如图,A,B两点在双曲线y=(x>0)上,分别过A,B两点向坐标轴作垂线,已知S阴影=1,则S1+S2的值为 .
8.点P,Q,R在反比例函数y=(常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3.若OE=ED=DC,S1+S3=27,则S2的值为 .
【练能力】
9.【石家庄期末】如图,在平面直角坐标系中,过x轴正半轴上任意一点P作y轴的平行线,分别交反比例函数y=(x>0),y=-(x>0)的图象于点A,B.若C是y轴上任意一点,则△ABC的面积为 ( )
A.9 B.6 C. D.3
10.【石家庄月考】如图,A是反比例函数y=(x>0)的图象上任意一点,AB∥x轴,且交反比例函数y=-(x<0)的图象于点B,以AB为边作平行四边形ABCD,点C,D在x轴上,则S ABCD= .
11.如图,一次函数y=kx+b与反比例函数y=(其中mk≠0)的图象交于A(-4,2),B(2,n)两点.
(1)求一次函数和反比例函数的表达式.
(2)求△ABO的面积.
(3)请直接写出当一次函数值大于反比例函数值时x的取值范围.
【练素养】
12.【2020·江西中考】如图,在Rt△ABC中,∠ACB=90°,顶点A,B都在反比例函数y=(x>0)的图象上,直线AC⊥x轴,垂足为D,连接OA,OC,并延长OC交AB于点E,当AB=2OA时,E恰好为AB的中点,若∠AOD=45°,OA=2.
(1)求反比例函数的解析式.
(2)求∠EOD的度数.
参考答案
练基础
1.C 2.D 3.D 4.C 5.B 6.C 7.6 8. 9.C
10.5
11.【解析】(1)∵一次函数y=kx+b与反比例函数y=(mk≠0)的图象交于A(-4,2),B(2,n)两点,
∴m=-8,n=-4,
∴ 解得
∴一次函数的表达式为y=-x-2,
反比例函数的表达式为y=-.
(2)设直线AB交y轴于点C.
在y=-x-2中,令x=0,则y=-2.
∴OC=2,
∴S△ABO=S△AOC+S△BOC=×2×4+×2×2=6.
(3)x<-4或0
∴△AOD是等腰直角三角形.
∵OA=2,
∴OD=AD=2,
∴A(2,2).
∵顶点A在反比例函数y=(x>0)的图象上,
∴k=2×2=4,
∴反比例函数的解析式为y=(x>0).
(2)∵AB=2OA,E恰好为AB的中点,
∴OA=AE.
∵在Rt△ABC中,∠ACB=90°,
∴CE=AE=BE,
∴∠AOE=∠AEO,∠ECB=∠EBC.
∵∠AEO=∠ECB+∠EBC=2∠EBC,
又∵BC∥x轴,
∴∠EOD=∠ECB,
∴∠AOE=2∠EOD.
∵∠AOD=45°,
∴∠EOD=15°.
2
