27.2.1 课时2 由三边和两边夹角判定三角形相似 分层练习(含答案)2023-2024学年数学人教版九年级下册
文档属性
| 名称 | 27.2.1 课时2 由三边和两边夹角判定三角形相似 分层练习(含答案)2023-2024学年数学人教版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 161.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 16:08:15 | ||
图片预览

文档简介
27.2.1 课时2 由三边和两边夹角判定三角形相似
【练基础】
必备知识1 三边成比例的两个三角形相似
1.有甲,乙两个三角形,甲三角形的三边长分别为1,,,乙三角形的三边长分别为5,,,则甲、乙两个三角形 ( )
A.一定相似 B.一定不相似
C.不一定相似 D.无法判断
2.已知△ABC三边长是,,2,与△ABC相似的三角形三边长可能是 ( )
A.1,, B.1,,
C.1,, D.1,,
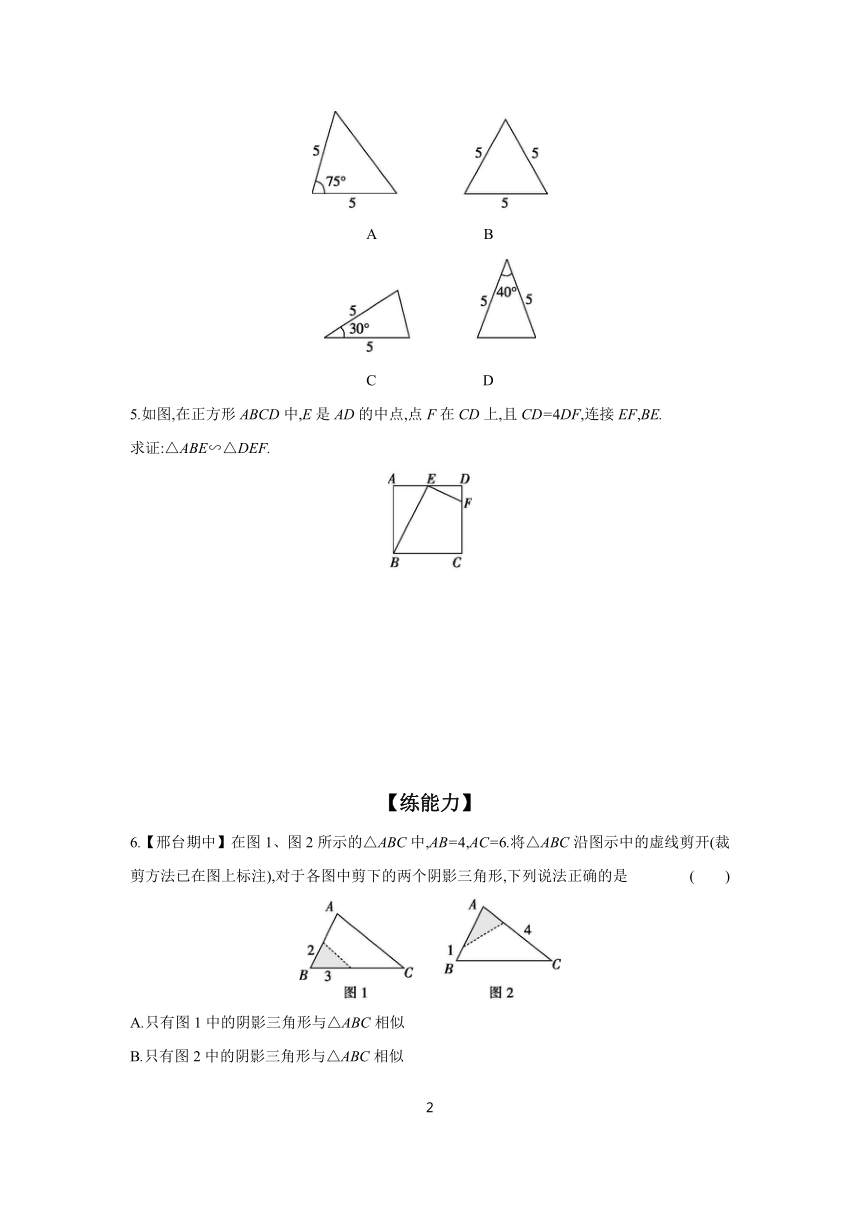
3.如图,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上,判断△ABC和△DEF是否相似,并说明理由.
必备知识2 两边和夹角判定三角形相似
4.【唐山月考】△ABC如图所示,则下列4个三角形中,与△ABC相似的是 ( )
A B
C D
5.如图,在正方形ABCD中,E是AD的中点,点F在CD上,且CD=4DF,连接EF,BE.
求证:△ABE∽△DEF.
【练能力】
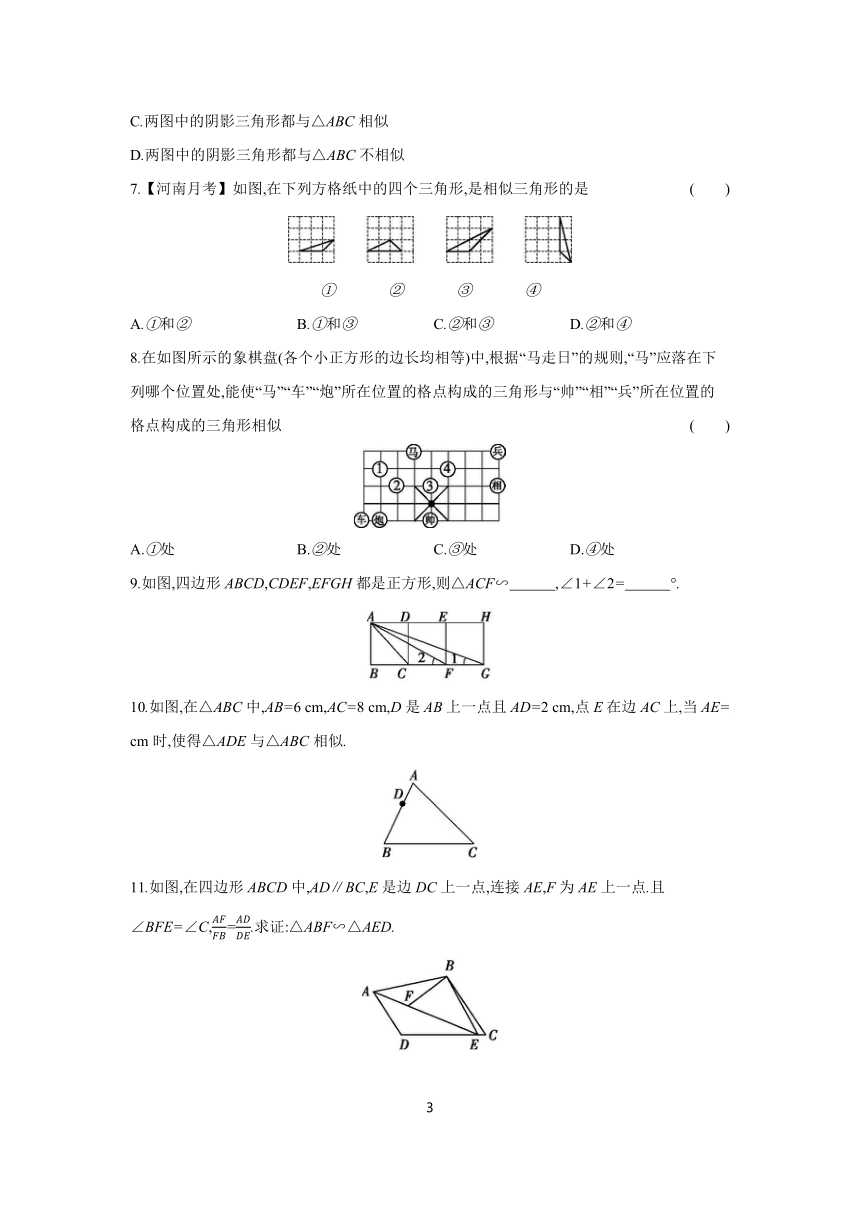
6.【邢台期中】在图1、图2所示的△ABC中,AB=4,AC=6.将△ABC沿图示中的虚线剪开(裁剪方法已在图上标注),对于各图中剪下的两个阴影三角形,下列说法正确的是 ( )
A.只有图1中的阴影三角形与△ABC相似
B.只有图2中的阴影三角形与△ABC相似
C.两图中的阴影三角形都与△ABC相似
D.两图中的阴影三角形都与△ABC不相似
7.【河南月考】如图,在下列方格纸中的四个三角形,是相似三角形的是 ( )
① ② ③ ④
A.①和② B.①和③ C.②和③ D.②和④
8.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似 ( )
A.①处 B.②处 C.③处 D.④处
9.如图,四边形ABCD,CDEF,EFGH都是正方形,则△ACF∽ ,∠1+∠2= °.
10.如图,在△ABC中,AB=6 cm,AC=8 cm,D是AB上一点且AD=2 cm,点E在边AC上,当AE= cm时,使得△ADE与△ABC相似.
11.如图,在四边形ABCD中,AD∥BC,E是边DC上一点,连接AE,F为AE上一点.且∠BFE=∠C,=.求证:△ABF∽△AED.
12.如图,在△ABC中,点D,E分别在边AB,AC上,连接DE.
(1)若AD·AB=AE·AC.求证:△ADE∽△ACB.
(2)若AB=8,AC=6,AD=3,直接写出:当AE= 时,△ADE与△ACB相似.
【练素养】
13.综合与探究:如图,在Rt△ABC中,直角边AC=3 cm,BC=4 cm.设P,Q分别为AB,BC上的动点,在点P自点A沿AB方向向点B做匀速移动的同时,点Q自点B沿BC方向向点C做匀速移动,它们移动的速度均为1 cm/s,当Q点到达C点时,P点就停止移动.设点P,Q移动的时间为t秒.△PBQ能否与△ABC相似 若能,求t的值;若不能,说明理由.
参考答案
练基础
1.A 2.A
3.【解析】△ABC和△DEF相似.
理由:由勾股定理,得AB=2,BC=5,AC=;
DF=2,DE=4,EF=2,
∴===.
∴△ABC∽△DEF.
4.C
5.【解析】设AB=4k,在正方形ABCD中,
AB=AD=CD=4k,∠A=∠D=90°.
∵E是AD的中点,CD=4DF,∴DF=k,AE=ED=2k,
∴==2,
∴△ABE∽△DEF.
练能力
6.B 7.B 8.B 9.△GCA 45 10.或1.5
11.【解析】∵AD∥BC,∴∠D+∠C=180°.
∵∠BFE+∠AFB=180°,∠BFE=∠C,
∴∠D=∠AFB.又∵=,
∴△ABF∽△AED.
12.【解析】(1)证明:∵AD·AB=AE·AC,
∴=.又∵∠A=∠A,
∴△ADE∽△ACB.
(2)若△ADE∽△ACB,则=,
即=,∴AE=4.
若△ADE∽△ABC,则=,
即=,∴AE=.
故答案为或4.
练素养
13.【解析】能.
理由:在Rt△ABC中,AC=3,BC=4,
∴AB==5,
∴BP=5-t,BQ=t.
当△PBQ∽△ABC时,=,即=,
解得t=;
当△PBQ∽△CBA时,=,即=,
解得t=,
即当△PBQ与直角三角形ABC相似时,t的值为或.
2
【练基础】
必备知识1 三边成比例的两个三角形相似
1.有甲,乙两个三角形,甲三角形的三边长分别为1,,,乙三角形的三边长分别为5,,,则甲、乙两个三角形 ( )
A.一定相似 B.一定不相似
C.不一定相似 D.无法判断
2.已知△ABC三边长是,,2,与△ABC相似的三角形三边长可能是 ( )
A.1,, B.1,,
C.1,, D.1,,
3.如图,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上,判断△ABC和△DEF是否相似,并说明理由.
必备知识2 两边和夹角判定三角形相似
4.【唐山月考】△ABC如图所示,则下列4个三角形中,与△ABC相似的是 ( )
A B
C D
5.如图,在正方形ABCD中,E是AD的中点,点F在CD上,且CD=4DF,连接EF,BE.
求证:△ABE∽△DEF.
【练能力】
6.【邢台期中】在图1、图2所示的△ABC中,AB=4,AC=6.将△ABC沿图示中的虚线剪开(裁剪方法已在图上标注),对于各图中剪下的两个阴影三角形,下列说法正确的是 ( )
A.只有图1中的阴影三角形与△ABC相似
B.只有图2中的阴影三角形与△ABC相似
C.两图中的阴影三角形都与△ABC相似
D.两图中的阴影三角形都与△ABC不相似
7.【河南月考】如图,在下列方格纸中的四个三角形,是相似三角形的是 ( )
① ② ③ ④
A.①和② B.①和③ C.②和③ D.②和④
8.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似 ( )
A.①处 B.②处 C.③处 D.④处
9.如图,四边形ABCD,CDEF,EFGH都是正方形,则△ACF∽ ,∠1+∠2= °.
10.如图,在△ABC中,AB=6 cm,AC=8 cm,D是AB上一点且AD=2 cm,点E在边AC上,当AE= cm时,使得△ADE与△ABC相似.
11.如图,在四边形ABCD中,AD∥BC,E是边DC上一点,连接AE,F为AE上一点.且∠BFE=∠C,=.求证:△ABF∽△AED.
12.如图,在△ABC中,点D,E分别在边AB,AC上,连接DE.
(1)若AD·AB=AE·AC.求证:△ADE∽△ACB.
(2)若AB=8,AC=6,AD=3,直接写出:当AE= 时,△ADE与△ACB相似.
【练素养】
13.综合与探究:如图,在Rt△ABC中,直角边AC=3 cm,BC=4 cm.设P,Q分别为AB,BC上的动点,在点P自点A沿AB方向向点B做匀速移动的同时,点Q自点B沿BC方向向点C做匀速移动,它们移动的速度均为1 cm/s,当Q点到达C点时,P点就停止移动.设点P,Q移动的时间为t秒.△PBQ能否与△ABC相似 若能,求t的值;若不能,说明理由.
参考答案
练基础
1.A 2.A
3.【解析】△ABC和△DEF相似.
理由:由勾股定理,得AB=2,BC=5,AC=;
DF=2,DE=4,EF=2,
∴===.
∴△ABC∽△DEF.
4.C
5.【解析】设AB=4k,在正方形ABCD中,
AB=AD=CD=4k,∠A=∠D=90°.
∵E是AD的中点,CD=4DF,∴DF=k,AE=ED=2k,
∴==2,
∴△ABE∽△DEF.
练能力
6.B 7.B 8.B 9.△GCA 45 10.或1.5
11.【解析】∵AD∥BC,∴∠D+∠C=180°.
∵∠BFE+∠AFB=180°,∠BFE=∠C,
∴∠D=∠AFB.又∵=,
∴△ABF∽△AED.
12.【解析】(1)证明:∵AD·AB=AE·AC,
∴=.又∵∠A=∠A,
∴△ADE∽△ACB.
(2)若△ADE∽△ACB,则=,
即=,∴AE=4.
若△ADE∽△ABC,则=,
即=,∴AE=.
故答案为或4.
练素养
13.【解析】能.
理由:在Rt△ABC中,AC=3,BC=4,
∴AB==5,
∴BP=5-t,BQ=t.
当△PBQ∽△ABC时,=,即=,
解得t=;
当△PBQ∽△CBA时,=,即=,
解得t=,
即当△PBQ与直角三角形ABC相似时,t的值为或.
2
