28.1 课时1 锐角三角函数(1)——正弦 分层练习(含答案)2023-2024学年数学人教版九年级下册
文档属性
| 名称 | 28.1 课时1 锐角三角函数(1)——正弦 分层练习(含答案)2023-2024学年数学人教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 173.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 16:16:48 | ||
图片预览

文档简介
28.1 课时1 锐角三角函数(1)——正弦
【练基础】
必备知识1 正弦的定义
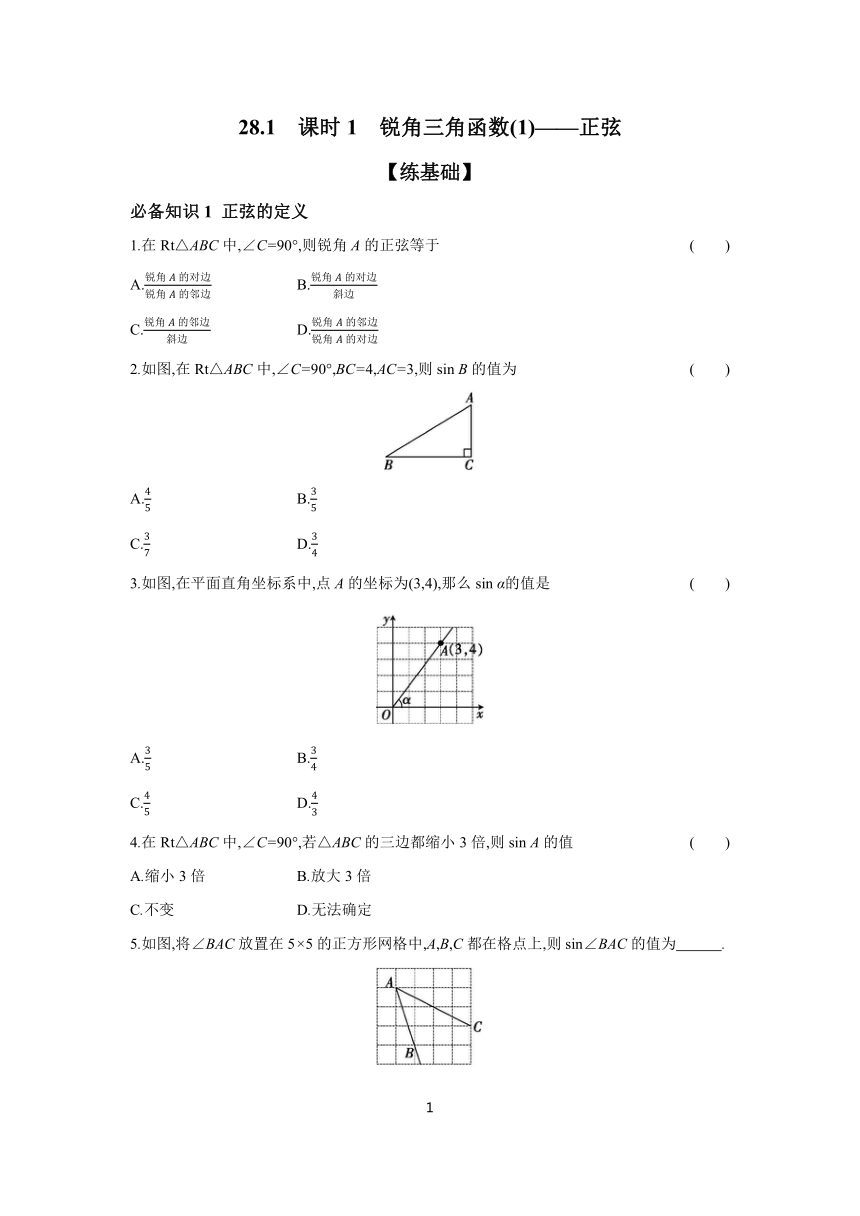
1.在Rt△ABC中,∠C=90°,则锐角A的正弦等于 ( )
A. B.
C. D.
2.如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sin B的值为 ( )
A. B.
C. D.
3.如图,在平面直角坐标系中,点A的坐标为(3,4),那么sin α的值是 ( )
A. B.
C. D.
4.在Rt△ABC中,∠C=90°,若△ABC的三边都缩小3倍,则sin A的值 ( )
A.缩小3倍 B.放大3倍
C.不变 D.无法确定
5.如图,将∠BAC放置在5×5的正方形网格中,A,B,C都在格点上,则sin∠BAC的值为 .
6.如图,在6×6的正方形网格中,△ABC的顶点A,B,C都在网格线上,且都是小正方形边的中点,则sin A= .
7.如图,在Rt△ABC中,∠C=90°,AB=12,BC=8,求sin A和sin B的值.
必备知识2 正弦的应用
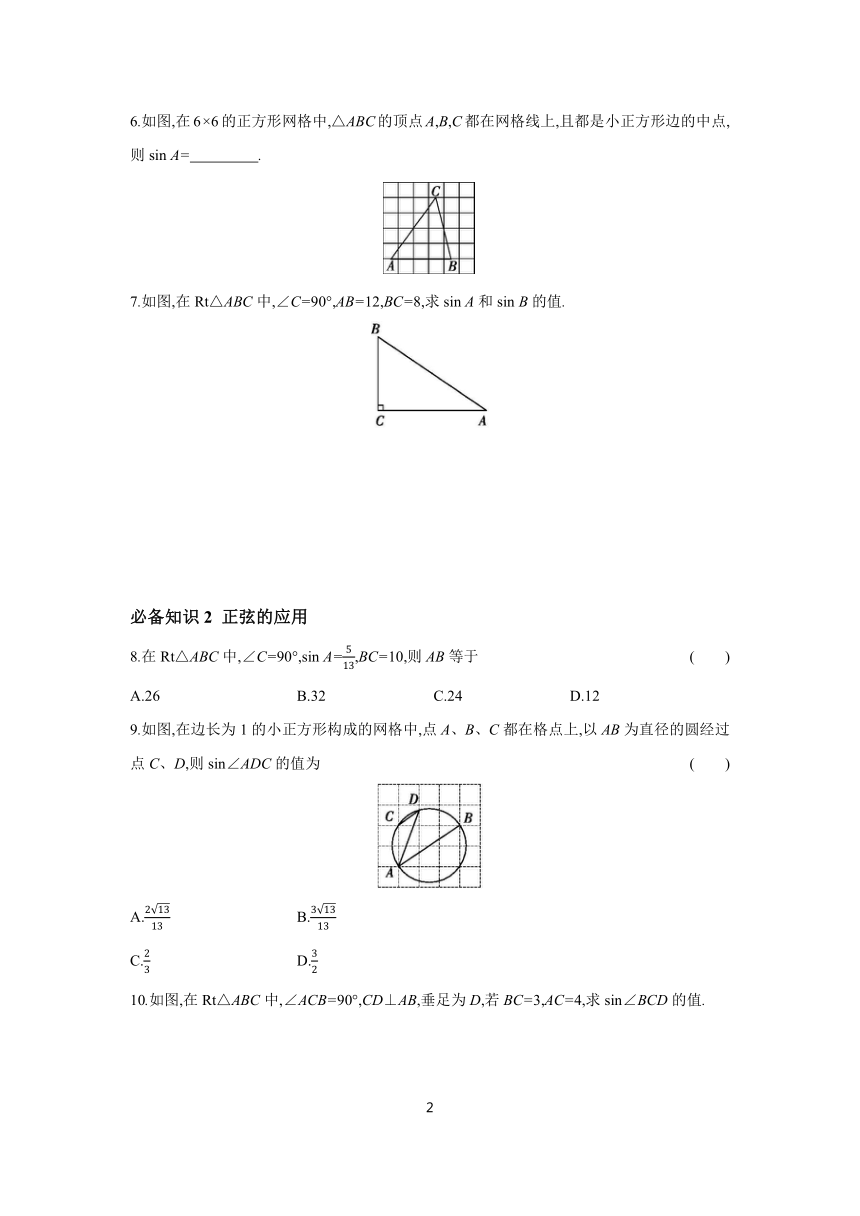
8.在Rt△ABC中,∠C=90°,sin A=,BC=10,则AB等于 ( )
A.26 B.32 C.24 D.12
9.如图,在边长为1的小正方形构成的网格中,点A、B、C都在格点上,以AB为直径的圆经过点C、D,则sin∠ADC的值为 ( )
A. B.
C. D.
10.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=3,AC=4,求sin∠BCD的值.
【练能力】
11.在Rt△ABC中,∠C=90°,若AB=4,sin A=,则斜边上的高为 ( )
A. B. C. D.
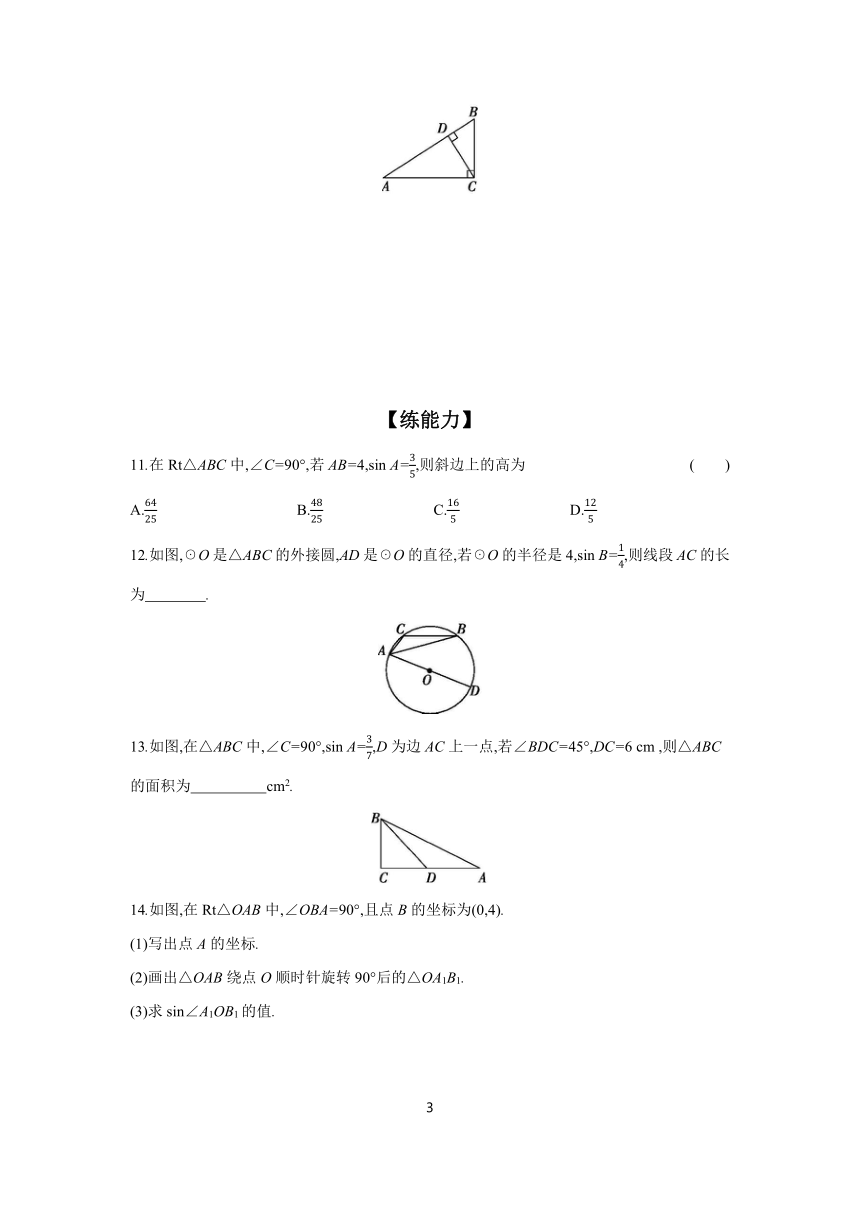
12.如图,☉O是△ABC的外接圆,AD是☉O的直径,若☉O的半径是4,sin B=,则线段AC的长为 .
13.如图,在△ABC中,∠C=90°,sin A=,D为边AC上一点,若∠BDC=45°,DC=6 cm ,则△ABC的面积为 cm2.
14.如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).
(1)写出点A的坐标.
(2)画出△OAB绕点O顺时针旋转90°后的△OA1B1.
(3)求sin∠A1OB1的值.
15.如图,在 ABCD中,AB=8,AD=5,sin A=,E是DC上一点,且BE=BC,求DE的长.
【练素养】
16.如图,在△ABC中,sin B=,点F在边BC上,AB=AF=5,过点F作EF⊥CB交AC于点E,且AE∶EC=3∶5.
(1)求BF的长.
(2)求sin C的值.
参考答案
练基础
1.B 2.B 3.C 4.C 5. 6.
7.【解析】在Rt△ABC中,∵AB=12,BC=8,
∴AC===4,
∴sin A===,
sin B===.
8.A 9.A
10.【解析】在Rt△ABC中,∵AC=4,BC=3,∴AB=5.
易证Rt△BCD∽Rt△BAC,∴∠BCD=∠BAC,
∴sin∠BCD=sin∠BAC==.
练能力
11.B 12.2 13.12
14.【解析】(1)从图上读出点A的坐标为(3,4).
(2)作图如下:
(3)根据勾股定理得OA1==5,
∴sin∠A1OB1=.
15.【解析】∵四边形ABCD是平行四边形,
∴∠C=∠A,DC=AB=8,BC=AD=5.
过点B作BF⊥CD,垂足为F(图略).
∵BE=BC,BF⊥CD,∴CE=2CF.
∵sin C==sin A=,
∴BF=4,∴CF=3,∴CE=6,
∴DE=DC-CE=2.
练素养
16.【解析】(1)如图,过点A作AD⊥CB,垂足为D.
在Rt△ABD中,∵sin B==,AB=5,
∴AD=4,∴BD=3.
∵AB=AF,AD⊥CB,
∴DF=BD=3,∴BF=6.
(2)∵EF⊥CB,AD⊥CB,
∴EF∥AD,∴=.
∵AE∶EC=3∶5,DF=3,
∴CF=5,∴CD=8.
在Rt△ACD中,AC==4,
∴sin C===.
2
【练基础】
必备知识1 正弦的定义
1.在Rt△ABC中,∠C=90°,则锐角A的正弦等于 ( )
A. B.
C. D.
2.如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sin B的值为 ( )
A. B.
C. D.
3.如图,在平面直角坐标系中,点A的坐标为(3,4),那么sin α的值是 ( )
A. B.
C. D.
4.在Rt△ABC中,∠C=90°,若△ABC的三边都缩小3倍,则sin A的值 ( )
A.缩小3倍 B.放大3倍
C.不变 D.无法确定
5.如图,将∠BAC放置在5×5的正方形网格中,A,B,C都在格点上,则sin∠BAC的值为 .
6.如图,在6×6的正方形网格中,△ABC的顶点A,B,C都在网格线上,且都是小正方形边的中点,则sin A= .
7.如图,在Rt△ABC中,∠C=90°,AB=12,BC=8,求sin A和sin B的值.
必备知识2 正弦的应用
8.在Rt△ABC中,∠C=90°,sin A=,BC=10,则AB等于 ( )
A.26 B.32 C.24 D.12
9.如图,在边长为1的小正方形构成的网格中,点A、B、C都在格点上,以AB为直径的圆经过点C、D,则sin∠ADC的值为 ( )
A. B.
C. D.
10.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=3,AC=4,求sin∠BCD的值.
【练能力】
11.在Rt△ABC中,∠C=90°,若AB=4,sin A=,则斜边上的高为 ( )
A. B. C. D.
12.如图,☉O是△ABC的外接圆,AD是☉O的直径,若☉O的半径是4,sin B=,则线段AC的长为 .
13.如图,在△ABC中,∠C=90°,sin A=,D为边AC上一点,若∠BDC=45°,DC=6 cm ,则△ABC的面积为 cm2.
14.如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).
(1)写出点A的坐标.
(2)画出△OAB绕点O顺时针旋转90°后的△OA1B1.
(3)求sin∠A1OB1的值.
15.如图,在 ABCD中,AB=8,AD=5,sin A=,E是DC上一点,且BE=BC,求DE的长.
【练素养】
16.如图,在△ABC中,sin B=,点F在边BC上,AB=AF=5,过点F作EF⊥CB交AC于点E,且AE∶EC=3∶5.
(1)求BF的长.
(2)求sin C的值.
参考答案
练基础
1.B 2.B 3.C 4.C 5. 6.
7.【解析】在Rt△ABC中,∵AB=12,BC=8,
∴AC===4,
∴sin A===,
sin B===.
8.A 9.A
10.【解析】在Rt△ABC中,∵AC=4,BC=3,∴AB=5.
易证Rt△BCD∽Rt△BAC,∴∠BCD=∠BAC,
∴sin∠BCD=sin∠BAC==.
练能力
11.B 12.2 13.12
14.【解析】(1)从图上读出点A的坐标为(3,4).
(2)作图如下:
(3)根据勾股定理得OA1==5,
∴sin∠A1OB1=.
15.【解析】∵四边形ABCD是平行四边形,
∴∠C=∠A,DC=AB=8,BC=AD=5.
过点B作BF⊥CD,垂足为F(图略).
∵BE=BC,BF⊥CD,∴CE=2CF.
∵sin C==sin A=,
∴BF=4,∴CF=3,∴CE=6,
∴DE=DC-CE=2.
练素养
16.【解析】(1)如图,过点A作AD⊥CB,垂足为D.
在Rt△ABD中,∵sin B==,AB=5,
∴AD=4,∴BD=3.
∵AB=AF,AD⊥CB,
∴DF=BD=3,∴BF=6.
(2)∵EF⊥CB,AD⊥CB,
∴EF∥AD,∴=.
∵AE∶EC=3∶5,DF=3,
∴CF=5,∴CD=8.
在Rt△ACD中,AC==4,
∴sin C===.
2
