(单元讲义)第二单元圆柱和圆锥-2023~2024学年六年级下册数学重难点讲义(西师大版)(含解析)
文档属性
| 名称 | (单元讲义)第二单元圆柱和圆锥-2023~2024学年六年级下册数学重难点讲义(西师大版)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 195.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 18:39:22 | ||
图片预览



文档简介
(单元讲义)第二单元圆柱和圆锥
1.圆柱的特征
【知识点归纳】
圆柱就是由两个大小相同的圆和一个侧面组成的.它的底面是完全相同的两个圆,侧面是一个曲面.
2.圆柱的展开图
【知识点归纳】
圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长方形(或正方形)的长等于圆柱底面的周长,宽等于圆柱的高.
3.圆柱的体积
【知识点归纳】
若一个圆柱底面半径为r,高为h,则圆柱的体积为V=πr2h
4.圆锥的体积
【知识点归纳】
圆锥体积底面积×高,用字母表示:
VShπr2h,(S表示底面积,h表示高)
5.圆柱的侧面积、表面积和体积
【知识点归纳】
圆柱的侧面积=底面的周长×高,用字母表示:
S侧=Ch(C表示底面的周长,h表示圆柱的高),或S侧=2πrh
圆柱的底面积=πr2
圆柱的表面积=侧面积+两个底面积,用字母表示:
S表=2πr2+2πrh
圆柱的体积=底面积×高,用字母表示:
V=πr2h.
一.选择题(共7小题)
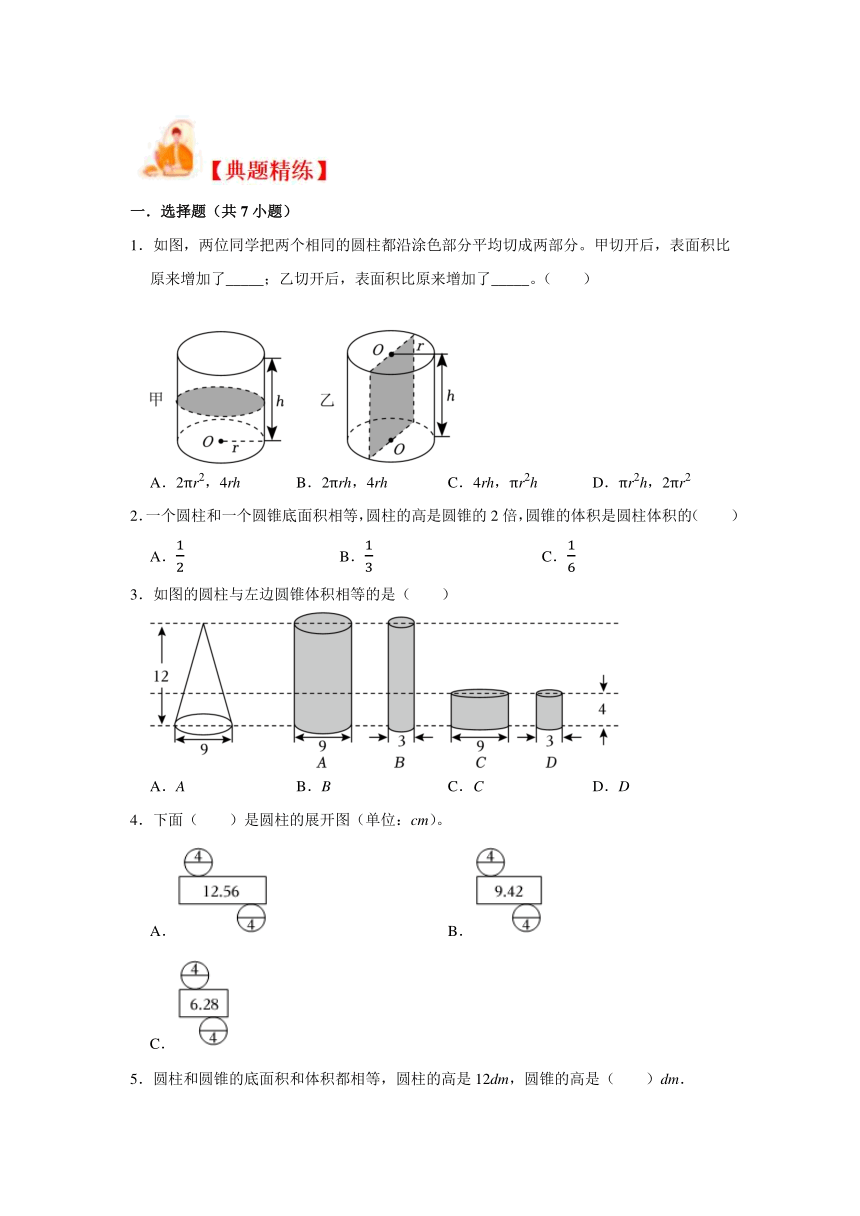
1.如图,两位同学把两个相同的圆柱都沿涂色部分平均切成两部分。甲切开后,表面积比原来增加了_____;乙切开后,表面积比原来增加了_____。( )
A.2πr2,4rh B.2πrh,4rh C.4rh,πr2h D.πr2h,2πr2
2.一个圆柱和一个圆锥底面积相等,圆柱的高是圆锥的2倍,圆锥的体积是圆柱体积的( )
A. B. C.
3.如图的圆柱与左边圆锥体积相等的是( )
A.A B.B C.C D.D
4.下面( )是圆柱的展开图(单位:cm)。
A. B.
C.
5.圆柱和圆锥的底面积和体积都相等,圆柱的高是12dm,圆锥的高是( )dm.
A.4 B.12 C.24 D.36
6.丽丽把一段长为10厘米、底面直径为6厘米的圆柱形火腿,如图放置,沿竖直方向切开,截面可能出现的情况是( )
A.直径为5厘米的圆形截面
B.长10厘米、宽6厘米的长方形截面
C.长10厘米、宽7厘米的长方形截面
7.把一个圆柱形薯片盒的商标纸展开是一个边长20厘米的正方形,下面关于这个薯片盒说法正确的是( )
A.底面半径是20厘米 B.底面周长是20厘米
C.底面直径是20厘米 D.底面积是20平方厘米
二.填空题(共7小题)
8.把一根长2米的圆柱截成3段,表面积增加了60平方分米,这个圆柱原来的体积是 立方分米。
9.把一个圆柱侧面展开,得到一个长31.4厘米,宽10厘米的长方形,这个圆柱的体积是 立方厘米.
10.把一个体积为1立方分米的正方体削成一个最大的圆柱,圆柱的体积是这个正方体体积的 %。
11.量得一个圆柱形粮囤底面周长是18.84米,高2米,它的体积是 立方米。
12.一个圆柱的底面半径是2厘米,高1.5厘米,它的侧面积是 平方厘米,表面积是 平方厘米,体积是 立方厘米。
13.圆柱的体积不变,如果底面半径扩大到原来的2倍,高应该 。
14.一个直角三角形,两条直角边分别是6厘米和2厘米,以较长直角边所在直线为轴旋转一周,所形成的立体图形是 括号内填“圆柱”或“圆锥”,所形成的立体图形的体积是 立方厘米。(π取3.14)
三.判断题(共8小题)
15.把一个圆柱形木料削成一个最大的圆锥,削去的部分是圆锥的2倍.
16.圆柱的体积等于和它等底等高的圆锥体积的3倍. .
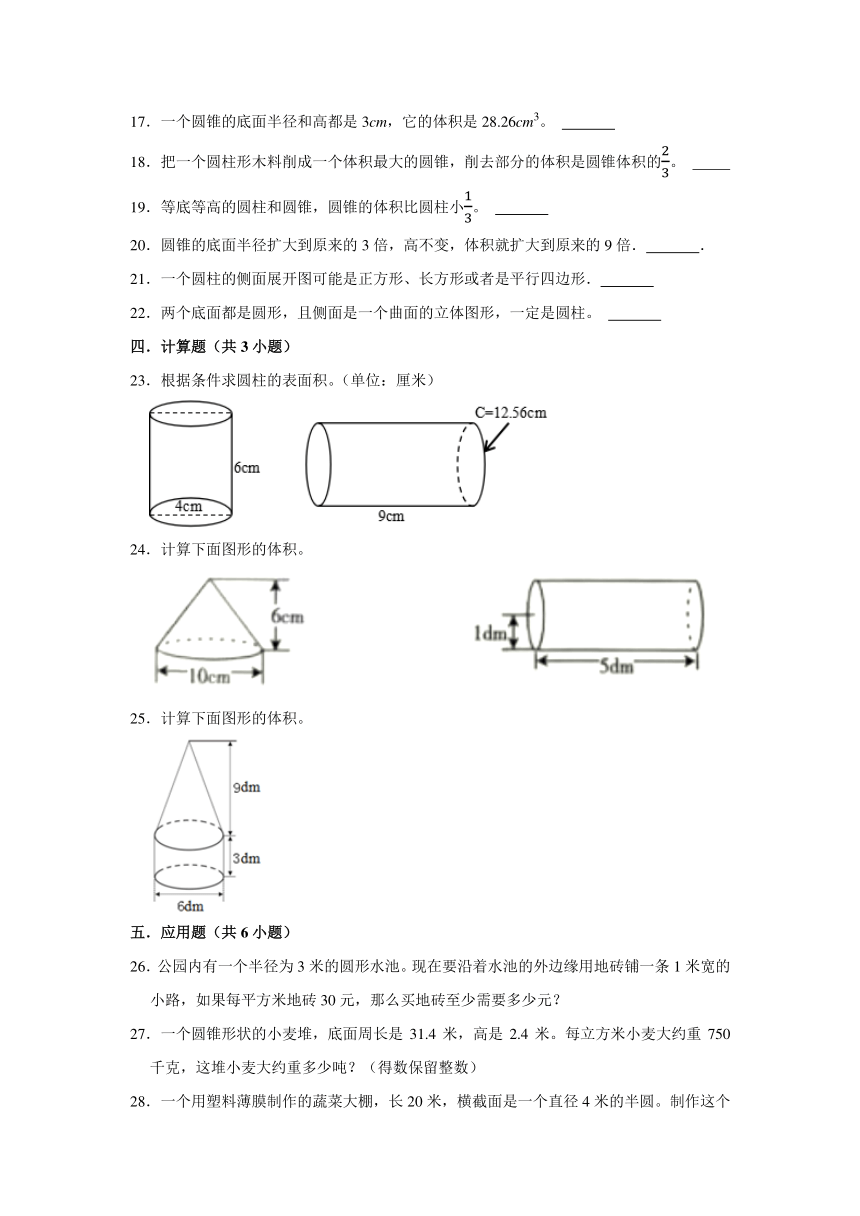
17.一个圆锥的底面半径和高都是3cm,它的体积是28.26cm3。
18.把一个圆柱形木料削成一个体积最大的圆锥,削去部分的体积是圆锥体积的。
19.等底等高的圆柱和圆锥,圆锥的体积比圆柱小。
20.圆锥的底面半径扩大到原来的3倍,高不变,体积就扩大到原来的9倍. .
21.一个圆柱的侧面展开图可能是正方形、长方形或者是平行四边形.
22.两个底面都是圆形,且侧面是一个曲面的立体图形,一定是圆柱。
四.计算题(共3小题)
23.根据条件求圆柱的表面积。(单位:厘米)
24.计算下面图形的体积。
25.计算下面图形的体积。
五.应用题(共6小题)
26.公园内有一个半径为3米的圆形水池。现在要沿着水池的外边缘用地砖铺一条1米宽的小路,如果每平方米地砖30元,那么买地砖至少需要多少元?
27.一个圆锥形状的小麦堆,底面周长是31.4米,高是2.4米。每立方米小麦大约重750千克,这堆小麦大约重多少吨?(得数保留整数)
28.一个用塑料薄膜制作的蔬菜大棚,长20米,横截面是一个直径4米的半圆。制作这个大棚至少需要塑料薄膜多少平方米?
29.把一个底面周长是6.28dm,高是6dm的圆柱形钢材,熔铸改造成了一个圆锥,这个圆锥的底面积是15.7dm ,它的高是多少分米?
30.一个底面半径是4厘米的圆柱形玻璃器皿里装有一部分水,水中浸没着一个高8厘米的圆锥体铅锤。当铅锤从水中取出后,水面下降了1厘米。这个圆锥体的底面积是多少平方厘米?(π取3.14)
31.一个圆锥形的沙堆,底面周长是12.56米,高6米,每立方米沙重约2吨,如果用一辆载重量为5吨地汽车去运,多少次可以远完?(π取3.14)
(单元讲义)第二单元圆柱和圆锥-2023~2024学年六年级下册数学重难点讲义(西师大版)
参考答案与试题解析
一.选择题(共7小题)
1.【答案】A
【分析】甲切分后,把圆柱切割成两部分后,表面积增加了2个圆柱的底面积;乙切分后,把圆柱切割成两部分后,表面积增加了2个以圆柱的高为长,直径为宽的长方形的面积;由此即可解答。
【解答】解:甲切分后,把圆柱切割成两部分后,表面积增加了:2πr2;
乙切分后,把圆柱切割成两部分后,表面积增加了:2×2rh=4rh。
故选:A。
【点评】抓住圆柱的切割特点,得出切割后增加部分的面的面积是解决本题的关键。
2.【答案】C
【分析】根据题意,可设圆柱、圆锥的底面积都为s,圆锥的高为1,则圆柱的高为2,根据圆柱的体积公式V=sh和圆锥的体积公式Vsh确定各自的体积,然后再用圆锥的体积除以圆柱的体积即可.
【解答】解:设圆柱、圆锥的底面积都为s,圆锥的高为1,则圆柱的高为2,
(s×1)÷(2s)
s÷2s,
,
答:圆锥的体积是圆柱体积的.
故选:C.
【点评】此题主要考查的是圆柱体体积公式和圆锥体体积公式的灵活应用.
3.【答案】C
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的。据此解答即可。
【解答】解:124
所以圆柱C与左边圆锥的体积相等。
故选:C。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
4.【答案】A
【分析】根据圆柱的展开图的特征,圆柱的两个底面是完全相同的两个圆,侧面展开是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高。根据圆的周长公式:把数据代入公式求出各图中圆的周长,然后与侧面展开图的长进行比较。据此解答即可。
【解答】解:A.3.14×4=12.56(厘米)
12.56=12.56
所以图A表示圆柱的展开图。
B.12.56≠9.42
所以图B不是圆柱的展开图。
C.12.56≠6.28
所以图C不是圆柱的展开图。
故选:A。
【点评】此题考查的目的是理解掌握圆柱展开图的图形及应用,特别是圆柱侧面展开图的特征及应用,关键是明确:圆柱的侧面沿高是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高。
5.【答案】D
【分析】根据圆柱的体积=底面积×高,圆锥的体积底面积×高,可得:当圆柱与圆锥的体积和底面积分别相等时,圆锥的高是圆柱的高的3倍,由此即可解决此类问题.
【解答】解:根据圆柱与圆锥的体积公式可得:当它们的体积与底面积分别相等时,圆锥的高是圆柱的高的3倍,
所以当圆柱的高是(12分)米,圆锥的高是:12×3=36(分米)
答:圆柱的高是(12分)米,圆锥的高是3(6分)米.
故选:D。
【点评】此题可得结论:体积与底面积分别相等时,圆锥的高是圆柱的高的3倍,由此结论即可解决此类问题.
6.【答案】B
【分析】丽丽把一段长为10厘米、底面直径为6厘米的圆柱形火腿,沿竖直方向切开会得到两个相同的长方形,长方形的长是圆柱的高,宽是圆柱的底面直径。
【解答】解:丽丽把一段长为10厘米、底面直径为6厘米的圆柱形火腿,如图放置,沿竖直方向切开可以得到长10厘米、宽6厘米的长方形截面。
故选:B。
【点评】本题考查了圆柱的特征。
7.【答案】B
【分析】它的侧面是一个边长20厘米的正方形,它的边长就是这个长方体的高,也是底面周长,据此选择即可。
【解答】解:把一个圆柱形薯片盒的商标纸展开是一个边长20厘米的正方形,下面关于这个薯片盒说法正确的是底面周长是20厘米。
故选:B。
【点评】解答有关长方体计算的实际问题,关键是理解周长20厘米的正方形的边长是薯片盒的哪部分,由此进行求解。
二.填空题(共7小题)
8.【答案】300。
【分析】根据锯木问题可知,截的段数比截的次数多1,截成3段需要截2次,每截1次就增加两个截面,那么截2次增加4个截面;已知截成3段后,表面积比原来增加60平方分米,由此可以求出圆柱体木料的底面积,再根据圆柱体的体积公式V=sh,代入数据计算即可。
【解答】解:2米=20分米
60÷4=15(平方分米)
15×20=300(立方分米)
答:这根木料的体积是300立方分米。
故答案为:300。
【点评】此题解答关键是理解锯木问题锯的次数比锯的段数少1,先求出底面积,再根据圆柱体的体积公式V=sh,列式解答即可。
9.【答案】见试题解答内容
【分析】要求这个圆柱的体积是多少立方厘米,圆柱的侧面展开后是长方形,长方形的长等于圆柱的底面周长,宽等于圆柱的高;根据“圆柱的半径=底面周长÷π÷2”先求出圆柱的底面半径,然后根据“圆柱的体积=πr2h,即可得出答案.
【解答】解:31.4÷3.14÷2=5(厘米),
3.14×52×10,
=785(立方厘米);
10÷3.14÷2≈1.59(厘米)
3.14×1.592×3.14≈24.93(立方厘米)
答:这个圆柱的体积是785立方厘米或24.93立方厘米.
故答案为:785或24.93.
【点评】此题解答应根据圆的周长公式,求出半径,然后再根据圆柱的体积计算公式,代入数值,进行解答.
10.【答案】78.5。
【分析】由题意可知,圆柱的底面直径和高都是1分米,根据圆柱的体积=底面积×高,解答此题即可。
【解答】解:1÷2=0.5(分米)
3.14×0.5×0.5×1=0.785
0.785÷1=0.785=78.5%
答:圆柱的体积是这个正方体体积的78.5%。
故答案为:78.5。
【点评】熟练掌握圆柱的体积公式,是解答此题的关键。
11.【答案】56.52。
【分析】根据圆的周长公式:C=2πr,据此求出圆柱形底面的半径,然后再根据圆的面积公式:S=πr2,据此求出圆柱的底面积,最后根据圆柱的体积公式:V=Sh,据此求出它的体积。
【解答】解:18.84÷3.14÷2
=6÷2
=3(米)
3.14×32×2
=3.14×9×2
=28.26×2
=56.52(立方米)
答:它的体积是56.52立方米。
故答案为:56.52。
【点评】本题考查圆柱的体积公式,熟记公式是解题的关键。
12.【答案】18.84,43.96,18.84。
【分析】圆柱的侧面积=底面周长×高;表面积=底面积×2+侧面积;体积=底面积×高,由此代入数据即可解答。
【解答】解:侧面积:3.14×2×2×1.5
=12.56×1.5
=18.84(平方厘米)
表面积:3.14×22×2+18.84
=3.14×4×2+18.84
=25.12+18.84
=43.96(平方厘米)
体积为:3.14×22×1.5
=3.14×4×1.5
=18.84(立方厘米)
答:这个圆柱的侧面积是18.84平方厘米,表面积是43.96平方厘米,体积是18.84立方厘米。
故答案为:18.84,43.96,18.84。
【点评】此题考查了圆柱的侧面积、表面积、体积公式的计算应用。
13.【答案】缩小到原来的四分之一。
【分析】根据圆柱的体积公式:V=πr2h,圆柱的底面半径扩大到原来的2倍,圆柱的底面积就扩大到原来的4倍,要使圆柱的体积不变,高应该缩小到原来的四分之一。据此解答。
【解答】解:2×2=4
4÷4=1
答:高应该缩小到原来的四分之一。
故答案为:缩小到原来的四分之一。
【点评】此题主要考查圆柱体积公式的灵活运用,积不变的性质及应用。
14.【答案】圆锥,25.12。
【分析】根据题意可知,以直角三角形的较长直角边所在直线为轴旋转一周,所形成的立体图形是圆锥,这个圆锥的底面半径的2厘米,高是6厘米,根据圆锥的体积公式:Vπr2h,把数据代入公式解答。
【解答】解:一个直角三角形,两条直角边分别是6厘米和2厘米,以较长直角边所在直线为轴旋转一周,所形成的立体图形是圆锥。
3.14×22×6
3.14×4×6
=25.12(立方厘米)
答:所形成的立体图形是圆锥,所形成的立体图形的体积是25.12立方厘米。
故答案为:圆锥,25.12。
【点评】此题考查的目的是理解掌握圆锥的特征及应用,圆锥的体积公式及应用,关键是熟记公式。
三.判断题(共8小题)
15.【答案】√
【分析】圆柱的体积是和它等底等高的圆锥体积的三倍,把圆柱削成最大的圆锥,则圆锥与圆柱等底等高,消去了两个圆锥的体积.也就是削去部分的体积是圆锥体积的2倍.
【解答】解:V圆柱=3V圆锥
(V圆柱﹣V圆锥)÷V圆锥
=2V圆锥÷V圆锥
=2
答:削去的部分是圆锥的2倍.
故答案为:√.
【点评】此题考查圆柱圆锥的体积,应明确:圆柱的体积是和它等底等高的圆锥体积的三倍.
16.【答案】见试题解答内容
【分析】圆柱的体积=底面积×高,圆锥的体积底面积×高,由此可以推理得出,等底等高的圆柱和圆锥的体积之比为:3:1.
【解答】解:令圆柱与圆锥的底面积为S,高位H,
所以圆柱的体积与圆锥的体积的比是:SH:SH=3:1.
所有等底等高的圆柱是圆锥的体积的3倍.
所以原题说法正确.
故答案为:√.
【点评】此题考查了等底等高的圆柱与圆锥体积的大小关系的推理方法.
17.【答案】√
【分析】根据圆锥的体积=底面积×高÷3,解答此题即可。
【解答】解:3.14×3×3×3÷3
=3.14×9
=28.26(立方厘米)
所以一个圆锥的底面半径和高都是3cm,它的体积是28.26cm3,这句话是正确的。
故答案为:√。
【点评】熟练掌握圆锥的体积公式,是解答此题的关键。
18.【答案】×
【分析】因为圆柱的体积等于和它等底等高的圆锥体积的3倍,所以削去部分的体积是圆锥体积的3﹣1=2,依此即可作出判断。
【解答】解:3﹣1=2
答:削去部分的体积是圆锥体积的2倍。
原题说法错误。
故答案为:×。
【点评】此题利用“圆柱的体积等于和它等底等高的圆锥体积的3倍”这一知识点来解答。
19.【答案】×
【分析】因为等底等高的圆锥的体积是圆柱体积的,把圆柱的体积看作单位“1”,根据求一个数比另一个少几分之几,用除法解答。
【解答】解:把圆柱的体积看作单位“1”,
(1)÷1
1
答:圆锥的体积比圆柱小。
所以原题说法错误。
故答案为:×。
【点评】本题主要考查等底等高的圆柱和圆锥体积之间的关系。
20.【答案】√
【分析】圆锥的体积底面积×高,若“高不变,底面半径扩大到原来的3倍”,则面积扩大到32倍,体积也扩大32倍.
【解答】解:因为圆锥的体积底面积×高,
如果一个圆锥体高不变,底面半径扩大到原来的3倍,这个圆锥的体积也扩大到原来的32=9倍;
故答案为:√.
【点评】此题主要考查圆锥的体积公式.
21.【答案】见试题解答内容
【分析】把一个圆柱沿高剪开,当圆柱的底面周长等于圆柱的高时,圆柱的侧面展开的图形是正方形;当圆柱的底面周长不等于圆柱的高时,圆柱的侧面展开的图形是长方形;当把一个圆柱不是沿高剪开,而是斜着剪开,得到的图形是平行四边形,由此做出判断.
【解答】解:因为把一个圆柱沿高剪开,当圆柱的底面周长等于圆柱的高时,圆柱的侧面展开的图形是正方形;
当圆柱的底面周长不等于圆柱的高时,圆柱的侧面展开的图形是长方形;
当把一个圆柱不是沿高剪开,而是斜着剪开,得到的图形是平行四边形;
所以,一个圆柱的侧面展开图可能是正方形、长方形或者是平行四边形.这种说法是正确的.
故答案为:√.
【点评】此题考查的目的是理解掌握圆柱侧面展开图的形状,明确:圆柱的侧面用不同的方法展开得到不同的图形.
22.【答案】×
【分析】从圆柱的定义入手进行分析:两个底面都是圆形,侧面是一个曲面的立体图形,不一定都是圆柱,圆柱上下两个底面面积相等,否则就不是圆柱。
【解答】解:根据圆柱的定义:圆柱是由两个大小相等、相互平行的圆形(底面)以及连接两个底面的一个曲面(侧面)围成的几何体。可知原题没有强调上下两个底面相等,说法不严密,所以错误。
故答案为:×。
【点评】本题考查了圆柱的特征的掌握能力。解题关键是牢记圆柱上下底面是大小相等的两个圆。
四.计算题(共3小题)
23.【答案】(1)100.48平方厘米;
(2)138.16平方厘米。
【分析】根据圆柱的表面积公式:S表=S侧+S底×2,把数据代入公式解答。
【解答】解:(1)3.14×4×6+3.14×(4÷2)2×2
=12.56×6+3.14×4×2
=75.36+25.12
=100.48(平方厘米)
答:它的表面积是100.48平方厘米。
(2)12.56×9+3.14×(12.56÷3.14÷2)2×2
=113.04+3.14×4×2
=113.04+25.12
=138.16(平方厘米)
答:它的表面积是138.16平方厘米。
【点评】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
24.【答案】157立方厘米;15.7立方分米。
【分析】圆锥的体积公式:Vπr2h,根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×(10÷2)2×6
3.14×25×6
=157(立方厘米)
3.14÷12×5
=3.14×1×5
=15.7(立方分米)
答:圆锥的体积是157立方厘米;圆柱的体积是15.7立方分米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
25.【答案】169.56立方分米。
【分析】该图形由一个圆柱和一个圆锥组成,利用圆柱的体积公式:V=πr2h,圆锥的体积公式:Vπr2h,计算即可。
【解答】解:3.14×(6÷2)2×3+3.14×(6÷2)2×9
=3.14×32×3+3.14×32×9
=84.78+84.78
=169.56(立方分米)
答:这个几何体的体积是169.56立方分米。
【点评】本题主要考查组合图形的体积,关键是把不规则几何体分成规则几何体,利用规则几何体的体积公式计算。
五.应用题(共6小题)
26.【答案】695.4。
【分析】根据题意可知,小路的面积是圆环形,根据环形面积公式:S环形=π(R2﹣r2),把数据代入公式求出环形面积,再乘以每平方地砖的价格,即可得出答案。
【解答】解:3+1=4(米)
3.14×(42﹣32)
=3.14×7
=21.98(平方米)
21.98×30=659.4(元)
答:买地砖至少需要659.4元。
【点评】此题主要考查环形面积公式的灵活运用,关键是熟记公式。
27.【答案】47吨。
【分析】先求出底面半径,根据圆锥体积=底面积×高÷3,求出小麦堆体积,用小麦体积乘每立方米质量即可,注意将千克转换成吨。
【解答】解:3.14×(31.4÷3.14÷2)2×2.4×750
3.14×25×2.4×750
=62.8×750
=47100(千克)
47100千克≈47吨。
答:这堆小麦大约重47吨。
【点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
28.【答案】138.16平方米。
【分析】要求需要多少平方米的塑料薄膜,就是求这个底面半径为2米,高为20米的圆柱的表面积的一半,利用圆柱的表面积=底面积×2+侧面积,代入数据即可计算得出。
【解答】解:4÷2=2(米)
(3.14×22×2+3.14×2×2×20)÷2
=(25.12+251.2)÷2
=276.32÷2
=138.16(平方米)
答:至少需要138.16平方米的塑料薄膜。
【点评】此题考查了公式圆柱的表面积=底面积×2+侧面积在实际问题中的灵活应用。
29.【答案】3.6分米。
【分析】根据圆柱体积=底面积×高,求出圆柱体积,就是圆锥体积,再根据圆锥高=圆锥体积×3÷底面积,即可解答。
【解答】解:[3.14×(6.28÷3.14÷2)2×6]×3÷15.7
=[3.14×1×6]×3÷15.7
=18.84×3÷15.7
=56.52÷15.7
=3.6(分米)
答:它的高是3.6分米。
【点评】本题考查的是圆锥体积和圆柱体积,熟记公式是解答关键。
30.【答案】18.84平方厘米。
【分析】圆锥体的体积就是1厘米高的圆柱体体积,根据圆柱体积=底面积×高,求出圆锥体铅锤的体积,再根据圆锥体的底面积=圆锥体体积×3÷高,即可解答。
【解答】解:3.14×4×4×1×3÷8
=150.72÷8
=18.84(平方厘米)
答:这个圆锥体的底面积是18.84平方厘米。
【点评】本题考查的是圆柱和圆锥体的体积的计算,熟记公式是解答关键。
31.【答案】11次。
【分析】首先根据圆锥的体积公式:Vπr2h,把数据代入公式求出这堆沙的体积,用沙的体积乘每立方米沙的质量求出这堆沙有多少吨,然后根据“包含”除法的意义,用除法解答。
【解答】解:3.14×(12.56÷3.14÷2)2×6×2÷5
3.14×4×6×2÷5
=25.12×2÷5
=50.24÷5
≈11(次)
答:11次可以运完。
【点评】此题主要考查圆锥体积公式的灵活运用,“包含”除法的意义及应用,关键是熟记公式。
1.圆柱的特征
【知识点归纳】
圆柱就是由两个大小相同的圆和一个侧面组成的.它的底面是完全相同的两个圆,侧面是一个曲面.
2.圆柱的展开图
【知识点归纳】
圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长方形(或正方形)的长等于圆柱底面的周长,宽等于圆柱的高.
3.圆柱的体积
【知识点归纳】
若一个圆柱底面半径为r,高为h,则圆柱的体积为V=πr2h
4.圆锥的体积
【知识点归纳】
圆锥体积底面积×高,用字母表示:
VShπr2h,(S表示底面积,h表示高)
5.圆柱的侧面积、表面积和体积
【知识点归纳】
圆柱的侧面积=底面的周长×高,用字母表示:
S侧=Ch(C表示底面的周长,h表示圆柱的高),或S侧=2πrh
圆柱的底面积=πr2
圆柱的表面积=侧面积+两个底面积,用字母表示:
S表=2πr2+2πrh
圆柱的体积=底面积×高,用字母表示:
V=πr2h.
一.选择题(共7小题)
1.如图,两位同学把两个相同的圆柱都沿涂色部分平均切成两部分。甲切开后,表面积比原来增加了_____;乙切开后,表面积比原来增加了_____。( )
A.2πr2,4rh B.2πrh,4rh C.4rh,πr2h D.πr2h,2πr2
2.一个圆柱和一个圆锥底面积相等,圆柱的高是圆锥的2倍,圆锥的体积是圆柱体积的( )
A. B. C.
3.如图的圆柱与左边圆锥体积相等的是( )
A.A B.B C.C D.D
4.下面( )是圆柱的展开图(单位:cm)。
A. B.
C.
5.圆柱和圆锥的底面积和体积都相等,圆柱的高是12dm,圆锥的高是( )dm.
A.4 B.12 C.24 D.36
6.丽丽把一段长为10厘米、底面直径为6厘米的圆柱形火腿,如图放置,沿竖直方向切开,截面可能出现的情况是( )
A.直径为5厘米的圆形截面
B.长10厘米、宽6厘米的长方形截面
C.长10厘米、宽7厘米的长方形截面
7.把一个圆柱形薯片盒的商标纸展开是一个边长20厘米的正方形,下面关于这个薯片盒说法正确的是( )
A.底面半径是20厘米 B.底面周长是20厘米
C.底面直径是20厘米 D.底面积是20平方厘米
二.填空题(共7小题)
8.把一根长2米的圆柱截成3段,表面积增加了60平方分米,这个圆柱原来的体积是 立方分米。
9.把一个圆柱侧面展开,得到一个长31.4厘米,宽10厘米的长方形,这个圆柱的体积是 立方厘米.
10.把一个体积为1立方分米的正方体削成一个最大的圆柱,圆柱的体积是这个正方体体积的 %。
11.量得一个圆柱形粮囤底面周长是18.84米,高2米,它的体积是 立方米。
12.一个圆柱的底面半径是2厘米,高1.5厘米,它的侧面积是 平方厘米,表面积是 平方厘米,体积是 立方厘米。
13.圆柱的体积不变,如果底面半径扩大到原来的2倍,高应该 。
14.一个直角三角形,两条直角边分别是6厘米和2厘米,以较长直角边所在直线为轴旋转一周,所形成的立体图形是 括号内填“圆柱”或“圆锥”,所形成的立体图形的体积是 立方厘米。(π取3.14)
三.判断题(共8小题)
15.把一个圆柱形木料削成一个最大的圆锥,削去的部分是圆锥的2倍.
16.圆柱的体积等于和它等底等高的圆锥体积的3倍. .
17.一个圆锥的底面半径和高都是3cm,它的体积是28.26cm3。
18.把一个圆柱形木料削成一个体积最大的圆锥,削去部分的体积是圆锥体积的。
19.等底等高的圆柱和圆锥,圆锥的体积比圆柱小。
20.圆锥的底面半径扩大到原来的3倍,高不变,体积就扩大到原来的9倍. .
21.一个圆柱的侧面展开图可能是正方形、长方形或者是平行四边形.
22.两个底面都是圆形,且侧面是一个曲面的立体图形,一定是圆柱。
四.计算题(共3小题)
23.根据条件求圆柱的表面积。(单位:厘米)
24.计算下面图形的体积。
25.计算下面图形的体积。
五.应用题(共6小题)
26.公园内有一个半径为3米的圆形水池。现在要沿着水池的外边缘用地砖铺一条1米宽的小路,如果每平方米地砖30元,那么买地砖至少需要多少元?
27.一个圆锥形状的小麦堆,底面周长是31.4米,高是2.4米。每立方米小麦大约重750千克,这堆小麦大约重多少吨?(得数保留整数)
28.一个用塑料薄膜制作的蔬菜大棚,长20米,横截面是一个直径4米的半圆。制作这个大棚至少需要塑料薄膜多少平方米?
29.把一个底面周长是6.28dm,高是6dm的圆柱形钢材,熔铸改造成了一个圆锥,这个圆锥的底面积是15.7dm ,它的高是多少分米?
30.一个底面半径是4厘米的圆柱形玻璃器皿里装有一部分水,水中浸没着一个高8厘米的圆锥体铅锤。当铅锤从水中取出后,水面下降了1厘米。这个圆锥体的底面积是多少平方厘米?(π取3.14)
31.一个圆锥形的沙堆,底面周长是12.56米,高6米,每立方米沙重约2吨,如果用一辆载重量为5吨地汽车去运,多少次可以远完?(π取3.14)
(单元讲义)第二单元圆柱和圆锥-2023~2024学年六年级下册数学重难点讲义(西师大版)
参考答案与试题解析
一.选择题(共7小题)
1.【答案】A
【分析】甲切分后,把圆柱切割成两部分后,表面积增加了2个圆柱的底面积;乙切分后,把圆柱切割成两部分后,表面积增加了2个以圆柱的高为长,直径为宽的长方形的面积;由此即可解答。
【解答】解:甲切分后,把圆柱切割成两部分后,表面积增加了:2πr2;
乙切分后,把圆柱切割成两部分后,表面积增加了:2×2rh=4rh。
故选:A。
【点评】抓住圆柱的切割特点,得出切割后增加部分的面的面积是解决本题的关键。
2.【答案】C
【分析】根据题意,可设圆柱、圆锥的底面积都为s,圆锥的高为1,则圆柱的高为2,根据圆柱的体积公式V=sh和圆锥的体积公式Vsh确定各自的体积,然后再用圆锥的体积除以圆柱的体积即可.
【解答】解:设圆柱、圆锥的底面积都为s,圆锥的高为1,则圆柱的高为2,
(s×1)÷(2s)
s÷2s,
,
答:圆锥的体积是圆柱体积的.
故选:C.
【点评】此题主要考查的是圆柱体体积公式和圆锥体体积公式的灵活应用.
3.【答案】C
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的。据此解答即可。
【解答】解:124
所以圆柱C与左边圆锥的体积相等。
故选:C。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
4.【答案】A
【分析】根据圆柱的展开图的特征,圆柱的两个底面是完全相同的两个圆,侧面展开是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高。根据圆的周长公式:把数据代入公式求出各图中圆的周长,然后与侧面展开图的长进行比较。据此解答即可。
【解答】解:A.3.14×4=12.56(厘米)
12.56=12.56
所以图A表示圆柱的展开图。
B.12.56≠9.42
所以图B不是圆柱的展开图。
C.12.56≠6.28
所以图C不是圆柱的展开图。
故选:A。
【点评】此题考查的目的是理解掌握圆柱展开图的图形及应用,特别是圆柱侧面展开图的特征及应用,关键是明确:圆柱的侧面沿高是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高。
5.【答案】D
【分析】根据圆柱的体积=底面积×高,圆锥的体积底面积×高,可得:当圆柱与圆锥的体积和底面积分别相等时,圆锥的高是圆柱的高的3倍,由此即可解决此类问题.
【解答】解:根据圆柱与圆锥的体积公式可得:当它们的体积与底面积分别相等时,圆锥的高是圆柱的高的3倍,
所以当圆柱的高是(12分)米,圆锥的高是:12×3=36(分米)
答:圆柱的高是(12分)米,圆锥的高是3(6分)米.
故选:D。
【点评】此题可得结论:体积与底面积分别相等时,圆锥的高是圆柱的高的3倍,由此结论即可解决此类问题.
6.【答案】B
【分析】丽丽把一段长为10厘米、底面直径为6厘米的圆柱形火腿,沿竖直方向切开会得到两个相同的长方形,长方形的长是圆柱的高,宽是圆柱的底面直径。
【解答】解:丽丽把一段长为10厘米、底面直径为6厘米的圆柱形火腿,如图放置,沿竖直方向切开可以得到长10厘米、宽6厘米的长方形截面。
故选:B。
【点评】本题考查了圆柱的特征。
7.【答案】B
【分析】它的侧面是一个边长20厘米的正方形,它的边长就是这个长方体的高,也是底面周长,据此选择即可。
【解答】解:把一个圆柱形薯片盒的商标纸展开是一个边长20厘米的正方形,下面关于这个薯片盒说法正确的是底面周长是20厘米。
故选:B。
【点评】解答有关长方体计算的实际问题,关键是理解周长20厘米的正方形的边长是薯片盒的哪部分,由此进行求解。
二.填空题(共7小题)
8.【答案】300。
【分析】根据锯木问题可知,截的段数比截的次数多1,截成3段需要截2次,每截1次就增加两个截面,那么截2次增加4个截面;已知截成3段后,表面积比原来增加60平方分米,由此可以求出圆柱体木料的底面积,再根据圆柱体的体积公式V=sh,代入数据计算即可。
【解答】解:2米=20分米
60÷4=15(平方分米)
15×20=300(立方分米)
答:这根木料的体积是300立方分米。
故答案为:300。
【点评】此题解答关键是理解锯木问题锯的次数比锯的段数少1,先求出底面积,再根据圆柱体的体积公式V=sh,列式解答即可。
9.【答案】见试题解答内容
【分析】要求这个圆柱的体积是多少立方厘米,圆柱的侧面展开后是长方形,长方形的长等于圆柱的底面周长,宽等于圆柱的高;根据“圆柱的半径=底面周长÷π÷2”先求出圆柱的底面半径,然后根据“圆柱的体积=πr2h,即可得出答案.
【解答】解:31.4÷3.14÷2=5(厘米),
3.14×52×10,
=785(立方厘米);
10÷3.14÷2≈1.59(厘米)
3.14×1.592×3.14≈24.93(立方厘米)
答:这个圆柱的体积是785立方厘米或24.93立方厘米.
故答案为:785或24.93.
【点评】此题解答应根据圆的周长公式,求出半径,然后再根据圆柱的体积计算公式,代入数值,进行解答.
10.【答案】78.5。
【分析】由题意可知,圆柱的底面直径和高都是1分米,根据圆柱的体积=底面积×高,解答此题即可。
【解答】解:1÷2=0.5(分米)
3.14×0.5×0.5×1=0.785
0.785÷1=0.785=78.5%
答:圆柱的体积是这个正方体体积的78.5%。
故答案为:78.5。
【点评】熟练掌握圆柱的体积公式,是解答此题的关键。
11.【答案】56.52。
【分析】根据圆的周长公式:C=2πr,据此求出圆柱形底面的半径,然后再根据圆的面积公式:S=πr2,据此求出圆柱的底面积,最后根据圆柱的体积公式:V=Sh,据此求出它的体积。
【解答】解:18.84÷3.14÷2
=6÷2
=3(米)
3.14×32×2
=3.14×9×2
=28.26×2
=56.52(立方米)
答:它的体积是56.52立方米。
故答案为:56.52。
【点评】本题考查圆柱的体积公式,熟记公式是解题的关键。
12.【答案】18.84,43.96,18.84。
【分析】圆柱的侧面积=底面周长×高;表面积=底面积×2+侧面积;体积=底面积×高,由此代入数据即可解答。
【解答】解:侧面积:3.14×2×2×1.5
=12.56×1.5
=18.84(平方厘米)
表面积:3.14×22×2+18.84
=3.14×4×2+18.84
=25.12+18.84
=43.96(平方厘米)
体积为:3.14×22×1.5
=3.14×4×1.5
=18.84(立方厘米)
答:这个圆柱的侧面积是18.84平方厘米,表面积是43.96平方厘米,体积是18.84立方厘米。
故答案为:18.84,43.96,18.84。
【点评】此题考查了圆柱的侧面积、表面积、体积公式的计算应用。
13.【答案】缩小到原来的四分之一。
【分析】根据圆柱的体积公式:V=πr2h,圆柱的底面半径扩大到原来的2倍,圆柱的底面积就扩大到原来的4倍,要使圆柱的体积不变,高应该缩小到原来的四分之一。据此解答。
【解答】解:2×2=4
4÷4=1
答:高应该缩小到原来的四分之一。
故答案为:缩小到原来的四分之一。
【点评】此题主要考查圆柱体积公式的灵活运用,积不变的性质及应用。
14.【答案】圆锥,25.12。
【分析】根据题意可知,以直角三角形的较长直角边所在直线为轴旋转一周,所形成的立体图形是圆锥,这个圆锥的底面半径的2厘米,高是6厘米,根据圆锥的体积公式:Vπr2h,把数据代入公式解答。
【解答】解:一个直角三角形,两条直角边分别是6厘米和2厘米,以较长直角边所在直线为轴旋转一周,所形成的立体图形是圆锥。
3.14×22×6
3.14×4×6
=25.12(立方厘米)
答:所形成的立体图形是圆锥,所形成的立体图形的体积是25.12立方厘米。
故答案为:圆锥,25.12。
【点评】此题考查的目的是理解掌握圆锥的特征及应用,圆锥的体积公式及应用,关键是熟记公式。
三.判断题(共8小题)
15.【答案】√
【分析】圆柱的体积是和它等底等高的圆锥体积的三倍,把圆柱削成最大的圆锥,则圆锥与圆柱等底等高,消去了两个圆锥的体积.也就是削去部分的体积是圆锥体积的2倍.
【解答】解:V圆柱=3V圆锥
(V圆柱﹣V圆锥)÷V圆锥
=2V圆锥÷V圆锥
=2
答:削去的部分是圆锥的2倍.
故答案为:√.
【点评】此题考查圆柱圆锥的体积,应明确:圆柱的体积是和它等底等高的圆锥体积的三倍.
16.【答案】见试题解答内容
【分析】圆柱的体积=底面积×高,圆锥的体积底面积×高,由此可以推理得出,等底等高的圆柱和圆锥的体积之比为:3:1.
【解答】解:令圆柱与圆锥的底面积为S,高位H,
所以圆柱的体积与圆锥的体积的比是:SH:SH=3:1.
所有等底等高的圆柱是圆锥的体积的3倍.
所以原题说法正确.
故答案为:√.
【点评】此题考查了等底等高的圆柱与圆锥体积的大小关系的推理方法.
17.【答案】√
【分析】根据圆锥的体积=底面积×高÷3,解答此题即可。
【解答】解:3.14×3×3×3÷3
=3.14×9
=28.26(立方厘米)
所以一个圆锥的底面半径和高都是3cm,它的体积是28.26cm3,这句话是正确的。
故答案为:√。
【点评】熟练掌握圆锥的体积公式,是解答此题的关键。
18.【答案】×
【分析】因为圆柱的体积等于和它等底等高的圆锥体积的3倍,所以削去部分的体积是圆锥体积的3﹣1=2,依此即可作出判断。
【解答】解:3﹣1=2
答:削去部分的体积是圆锥体积的2倍。
原题说法错误。
故答案为:×。
【点评】此题利用“圆柱的体积等于和它等底等高的圆锥体积的3倍”这一知识点来解答。
19.【答案】×
【分析】因为等底等高的圆锥的体积是圆柱体积的,把圆柱的体积看作单位“1”,根据求一个数比另一个少几分之几,用除法解答。
【解答】解:把圆柱的体积看作单位“1”,
(1)÷1
1
答:圆锥的体积比圆柱小。
所以原题说法错误。
故答案为:×。
【点评】本题主要考查等底等高的圆柱和圆锥体积之间的关系。
20.【答案】√
【分析】圆锥的体积底面积×高,若“高不变,底面半径扩大到原来的3倍”,则面积扩大到32倍,体积也扩大32倍.
【解答】解:因为圆锥的体积底面积×高,
如果一个圆锥体高不变,底面半径扩大到原来的3倍,这个圆锥的体积也扩大到原来的32=9倍;
故答案为:√.
【点评】此题主要考查圆锥的体积公式.
21.【答案】见试题解答内容
【分析】把一个圆柱沿高剪开,当圆柱的底面周长等于圆柱的高时,圆柱的侧面展开的图形是正方形;当圆柱的底面周长不等于圆柱的高时,圆柱的侧面展开的图形是长方形;当把一个圆柱不是沿高剪开,而是斜着剪开,得到的图形是平行四边形,由此做出判断.
【解答】解:因为把一个圆柱沿高剪开,当圆柱的底面周长等于圆柱的高时,圆柱的侧面展开的图形是正方形;
当圆柱的底面周长不等于圆柱的高时,圆柱的侧面展开的图形是长方形;
当把一个圆柱不是沿高剪开,而是斜着剪开,得到的图形是平行四边形;
所以,一个圆柱的侧面展开图可能是正方形、长方形或者是平行四边形.这种说法是正确的.
故答案为:√.
【点评】此题考查的目的是理解掌握圆柱侧面展开图的形状,明确:圆柱的侧面用不同的方法展开得到不同的图形.
22.【答案】×
【分析】从圆柱的定义入手进行分析:两个底面都是圆形,侧面是一个曲面的立体图形,不一定都是圆柱,圆柱上下两个底面面积相等,否则就不是圆柱。
【解答】解:根据圆柱的定义:圆柱是由两个大小相等、相互平行的圆形(底面)以及连接两个底面的一个曲面(侧面)围成的几何体。可知原题没有强调上下两个底面相等,说法不严密,所以错误。
故答案为:×。
【点评】本题考查了圆柱的特征的掌握能力。解题关键是牢记圆柱上下底面是大小相等的两个圆。
四.计算题(共3小题)
23.【答案】(1)100.48平方厘米;
(2)138.16平方厘米。
【分析】根据圆柱的表面积公式:S表=S侧+S底×2,把数据代入公式解答。
【解答】解:(1)3.14×4×6+3.14×(4÷2)2×2
=12.56×6+3.14×4×2
=75.36+25.12
=100.48(平方厘米)
答:它的表面积是100.48平方厘米。
(2)12.56×9+3.14×(12.56÷3.14÷2)2×2
=113.04+3.14×4×2
=113.04+25.12
=138.16(平方厘米)
答:它的表面积是138.16平方厘米。
【点评】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
24.【答案】157立方厘米;15.7立方分米。
【分析】圆锥的体积公式:Vπr2h,根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×(10÷2)2×6
3.14×25×6
=157(立方厘米)
3.14÷12×5
=3.14×1×5
=15.7(立方分米)
答:圆锥的体积是157立方厘米;圆柱的体积是15.7立方分米。
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
25.【答案】169.56立方分米。
【分析】该图形由一个圆柱和一个圆锥组成,利用圆柱的体积公式:V=πr2h,圆锥的体积公式:Vπr2h,计算即可。
【解答】解:3.14×(6÷2)2×3+3.14×(6÷2)2×9
=3.14×32×3+3.14×32×9
=84.78+84.78
=169.56(立方分米)
答:这个几何体的体积是169.56立方分米。
【点评】本题主要考查组合图形的体积,关键是把不规则几何体分成规则几何体,利用规则几何体的体积公式计算。
五.应用题(共6小题)
26.【答案】695.4。
【分析】根据题意可知,小路的面积是圆环形,根据环形面积公式:S环形=π(R2﹣r2),把数据代入公式求出环形面积,再乘以每平方地砖的价格,即可得出答案。
【解答】解:3+1=4(米)
3.14×(42﹣32)
=3.14×7
=21.98(平方米)
21.98×30=659.4(元)
答:买地砖至少需要659.4元。
【点评】此题主要考查环形面积公式的灵活运用,关键是熟记公式。
27.【答案】47吨。
【分析】先求出底面半径,根据圆锥体积=底面积×高÷3,求出小麦堆体积,用小麦体积乘每立方米质量即可,注意将千克转换成吨。
【解答】解:3.14×(31.4÷3.14÷2)2×2.4×750
3.14×25×2.4×750
=62.8×750
=47100(千克)
47100千克≈47吨。
答:这堆小麦大约重47吨。
【点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
28.【答案】138.16平方米。
【分析】要求需要多少平方米的塑料薄膜,就是求这个底面半径为2米,高为20米的圆柱的表面积的一半,利用圆柱的表面积=底面积×2+侧面积,代入数据即可计算得出。
【解答】解:4÷2=2(米)
(3.14×22×2+3.14×2×2×20)÷2
=(25.12+251.2)÷2
=276.32÷2
=138.16(平方米)
答:至少需要138.16平方米的塑料薄膜。
【点评】此题考查了公式圆柱的表面积=底面积×2+侧面积在实际问题中的灵活应用。
29.【答案】3.6分米。
【分析】根据圆柱体积=底面积×高,求出圆柱体积,就是圆锥体积,再根据圆锥高=圆锥体积×3÷底面积,即可解答。
【解答】解:[3.14×(6.28÷3.14÷2)2×6]×3÷15.7
=[3.14×1×6]×3÷15.7
=18.84×3÷15.7
=56.52÷15.7
=3.6(分米)
答:它的高是3.6分米。
【点评】本题考查的是圆锥体积和圆柱体积,熟记公式是解答关键。
30.【答案】18.84平方厘米。
【分析】圆锥体的体积就是1厘米高的圆柱体体积,根据圆柱体积=底面积×高,求出圆锥体铅锤的体积,再根据圆锥体的底面积=圆锥体体积×3÷高,即可解答。
【解答】解:3.14×4×4×1×3÷8
=150.72÷8
=18.84(平方厘米)
答:这个圆锥体的底面积是18.84平方厘米。
【点评】本题考查的是圆柱和圆锥体的体积的计算,熟记公式是解答关键。
31.【答案】11次。
【分析】首先根据圆锥的体积公式:Vπr2h,把数据代入公式求出这堆沙的体积,用沙的体积乘每立方米沙的质量求出这堆沙有多少吨,然后根据“包含”除法的意义,用除法解答。
【解答】解:3.14×(12.56÷3.14÷2)2×6×2÷5
3.14×4×6×2÷5
=25.12×2÷5
=50.24÷5
≈11(次)
答:11次可以运完。
【点评】此题主要考查圆锥体积公式的灵活运用,“包含”除法的意义及应用,关键是熟记公式。
