2023-2024学年数学人教版九年级下册第二十八章 锐角三角函数 分层练习(含解析)
文档属性
| 名称 | 2023-2024学年数学人教版九年级下册第二十八章 锐角三角函数 分层练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 199.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 16:21:50 | ||
图片预览



文档简介
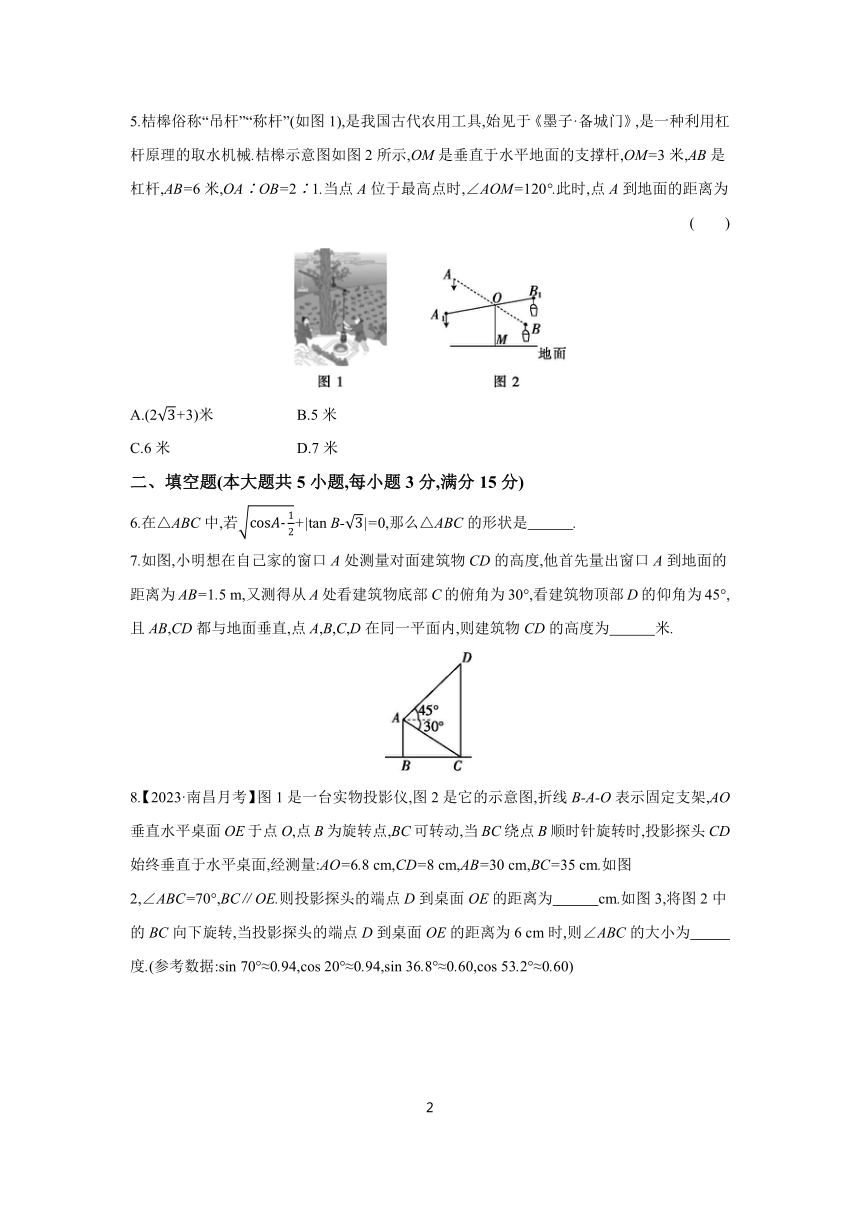
第二十八章 锐角三角函数 自我评估
(建议用时:60分钟 分值:50分)
一、选择题(本大题共5小题,每小题3分,满分15分)
1.已知α为锐角,且sin(90°-α)=,则α的度数是 ( )
A.30° B.45° C.60° D.75°
2.【2023·保定月考】如图,已知一台观测车对空中目标A进行观测,观测车从B点沿直线行驶到C点的过程中,仰角将 ( )
A.增大 B.减小
C.先增大,后减小 D.先减小,后增大
3.【2022·南昌月考】如图,点A,B,C都在边长为1的正方形格点上,连接AB,BC,则cos∠ABC的值为 ( )
A. B. C. D.1
4.如图,这是一把圆规的平面示意图,OA是支撑臂,OB是旋转臂.已知OA=OB=a,使用时,以点A为支撑点,笔芯端点B可绕点A旋转作出圆.若支撑臂与旋转臂的夹角∠AOB=2θ,则圆规能画出的圆的半径AB长度为 ( )
A.2asin θ B.asin 2θ
C.2atan θ D.atan 2θ
5.桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于《墨子·备城门》,是一种利用杠杆原理的取水机械.桔槔示意图如图2所示,OM是垂直于水平地面的支撑杆,OM=3米,AB是杠杆,AB=6米,OA∶OB=2∶1.当点A位于最高点时,∠AOM=120°.此时,点A到地面的距离为 ( )
A.(2+3)米 B.5米
C.6米 D.7米
二、填空题(本大题共5小题,每小题3分,满分15分)
6.在△ABC中,若+|tan B-|=0,那么△ABC的形状是 .
7.如图,小明想在自己家的窗口A处测量对面建筑物CD的高度,他首先量出窗口A到地面的距离为AB=1.5 m,又测得从A处看建筑物底部C的俯角为30°,看建筑物顶部D的仰角为45°,且AB,CD都与地面垂直,点A,B,C,D在同一平面内,则建筑物CD的高度为 米.
8.【2023·南昌月考】图1是一台实物投影仪,图2是它的示意图,折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面,经测量:AO=6.8 cm,CD=8 cm,AB=30 cm,BC=35 cm.如图2,∠ABC=70°,BC∥OE.则投影探头的端点D到桌面OE的距离为 cm.如图3,将图2中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6 cm时,则∠ABC的大小为 度.(参考数据:sin 70°≈0.94,cos 20°≈0.94,sin 36.8°≈0.60,cos 53.2°≈0.60)
9.【2023·唐山月考】如图,这是某型号机器人示意图,OA是垂直于工作台的移动基座,AB,BC为机械臂,OA=1 m,AB=5 m,BC=2 m,∠ABC=143°,机械臂端点C到工作台的距离CD=6 m.
(1)∠ABC的补角度数是 °.
(2)点A到直线BC的距离约是 m.
(3)OD的长约是 m.(结果精确到0.1 m)
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈2.24)
10.黑龙江亚布力地区的滑雪场在国内享誉盛名,如图,这是该地区某滑雪场的一段赛道示意图,AB段为助滑段,长为12米,坡角α为16°,一个曲面平台BCD连接了助滑坡AB与着陆坡DE.已知着陆坡DE的坡度i=1∶2.4,DE的长度为19.5米,B,D之间的垂直距离h为5.5米,则一人从A出发到E处下降的垂直距离约为 米.(参考数据:sin 16°≈0.28,cos 16°≈0.96,tan 16°≈0.29,结果保留一位小数)
三、解答题(本大题共2小题,满分20分)
11.(10分)如图,在△ABC中,BD⊥AC,AB=4,AC=3,∠A=30°.
(1)求AD的长.
(2)求sin C的值.
12.(10分)2022年11月29日,“神舟十五号”载人航天飞船搭载“明星”机械臂成功发射.2023年2月9日“神舟十五号”航天员进行了出舱活动,为了确保任务的圆满完成,航天员借助机械臂进行舱外作业.如图,这是处于工作状态的某型号手臂机器人示意图,OA是垂直于工作台的移动基座,AB,BC为机械臂,OA=1 m,AB=5 m,BC=2 m,∠ABC=145°,∠BCD=60°.
(1)求机械臂端点C到工作台的距离CD的长.(结果精确到0.1 m)
(2)求OD的长.(结果精确到0.1 m)
(参考数据:sin 25°≈0.42,cos 25°≈0.91,tan 25°≈0.47,≈1.41,≈1.73)
参考答案
1.C
2.C 【解析】当观测车从B点行驶到目标A的正下方的过程中,仰角逐渐增大,
行驶到目标A的正下方时,仰角最大,为90°,再继续行驶到C点的过程中,仰角逐渐减小.
故选C.
3.B
4.A 【解析】
如图,作OC⊥AB交AB于点C,
∵OA=OB,
∴OC平分∠AOB,点C平分AB.
∵∠AOB=2θ,
∴∠AOC=θ.
∵OA=OB=a,
∴AC=asin θ,
∴AB=2AC=2asin θ.
故选A.
5.B 【解析】
如图,过点O作EF⊥OM,过A作AG⊥EF于点G,
∵AB=6米,OA∶OB=2∶1,
∴OA=4米.
∵∠AOM=120°,∠EOM=90°,
∴∠AOE=30°.
在Rt△AOG中,AG=AO·sin 30°=2(米),
点A位于最高点时到地面的距离为2+3=5(米),
所以点A到地面的距离为5米.
故选B.
6.等边三角形 7.
8.27 33.2 【解析】过点A作AF⊥BC于点F,如图1,
则AF=AB·sin∠ABF=30·sin 70°≈28.2(cm),
∴投影探头的端点D到桌面OE的距离为AF+OA-CD=28.2+6.8-8=27(cm).
过点D作DH⊥OE于点H,过点B作BM⊥CD,与DC延长线相交于点M,过点A作AF⊥BM于点F,如图2,
则∠MBA=70°,
∴CM=AF+AO-DH-CD=28.2+6.8-6-8=21(cm),
∴sin∠MBC===0.6,
∴∠MBC=36.8°,
∴∠ABC=∠ABM-∠MBC=33.2°.
故答案为27;33.2.
9.(1)37 (2)3.0 (3)4.5
【解析】(1)∵∠ABC=143°,
∴∠ABC的补角是180°-143°=37°.
(2)如图,过点A作AE⊥BC交CB的延长线于点E,
在Rt△ABE中,
∴sin∠ABE=,
∴AE=AB·sin 37°≈3.0(m).
(3)如图,连接AC,过点A作AF⊥CD于点F,
∴四边形AFDO是矩形,
∴AF=DO,DF=OA=1(m),
∴CF=5(m).
在Rt△ABE中,
由勾股定理可知,BE==4(m),
∴CE=CB+BE=6(m).
在Rt△CEA中,
由勾股定理可知,AC2=32+62=45,
在Rt△ACF中,
由勾股定理可知,AF2=45-25=20,
∴AF=2≈4.5(m),
即OD≈4.5(m).
故答案为(1)37.
(2)3.0.
(3)4.5.
10.16.4 【解析】
如图,作BF⊥AP于点F,DG⊥AP于点G,DH⊥PE于点H,易知FG=h,GP=DH.在Rt△AFB中,sin 16°=,AB=12米,
∴AF=AB·sin 16°≈12×0.28=3.36(米).
设DH=x米,∵着陆坡DE的坡度i=1∶2.4,∴HE=2.4x,由勾股定理得,HE2+DH2=DE2,即(2.4x)2+x2=19.52,解得x=7.5,即DH=7.5(米).
∴一人从A出发到E处下降的垂直距离为AF+h+DH=3.36+5.5+7.5≈16.4(米).
11.【解析】(1)在Rt△ABD中,∠ADB=90°,AB=4,∠A=30°,
∴AD=AB·cos 30°=4×=2.
(2)∵AC=3,AD=2,
∴CD=AC-AD=.
∵∠ADB=90°,AB=4,∠A=30°,
∴BD=AB=2.
在Rt△CBD中,∠CDB=90°,BD=2,CD=,
∴BC==.
∴sin C===.
12.【解析】(1)如图,过点B作BE⊥CD于点E,过点B作BF⊥OD于点F,过点A作AG⊥BF于点G,
∴四边形BEDF是矩形,四边形AOFG是矩形,
∴BE=DF,BF=ED,∠EBF=90°,OA=GF=1米.
∵∠ABC=145°,∠BCD=60°,
∴∠CBE=30°,∠ABG=25°.
∵BC=2米,
∴CE=1米.
在Rt△ABG中,cos∠ABG=,
∴BG≈5×0.91≈4.6米,
∴BF=BG+GF=5.6米,
∴CD=CE+BF=1+5.6=6.6米.
答:机械臂端点C到工作台的距离CD的长6.6米.
(2)在Rt△BCE中,由勾股定理可知:BE=米,
在Rt△ABG中,
由勾股定理可知:AG=≈2.1米,
∴OF=AG≈2.1米,
∴OD=DF+OF≈3.8米.
答:OD的长为3.8米.
2
(建议用时:60分钟 分值:50分)
一、选择题(本大题共5小题,每小题3分,满分15分)
1.已知α为锐角,且sin(90°-α)=,则α的度数是 ( )
A.30° B.45° C.60° D.75°
2.【2023·保定月考】如图,已知一台观测车对空中目标A进行观测,观测车从B点沿直线行驶到C点的过程中,仰角将 ( )
A.增大 B.减小
C.先增大,后减小 D.先减小,后增大
3.【2022·南昌月考】如图,点A,B,C都在边长为1的正方形格点上,连接AB,BC,则cos∠ABC的值为 ( )
A. B. C. D.1
4.如图,这是一把圆规的平面示意图,OA是支撑臂,OB是旋转臂.已知OA=OB=a,使用时,以点A为支撑点,笔芯端点B可绕点A旋转作出圆.若支撑臂与旋转臂的夹角∠AOB=2θ,则圆规能画出的圆的半径AB长度为 ( )
A.2asin θ B.asin 2θ
C.2atan θ D.atan 2θ
5.桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于《墨子·备城门》,是一种利用杠杆原理的取水机械.桔槔示意图如图2所示,OM是垂直于水平地面的支撑杆,OM=3米,AB是杠杆,AB=6米,OA∶OB=2∶1.当点A位于最高点时,∠AOM=120°.此时,点A到地面的距离为 ( )
A.(2+3)米 B.5米
C.6米 D.7米
二、填空题(本大题共5小题,每小题3分,满分15分)
6.在△ABC中,若+|tan B-|=0,那么△ABC的形状是 .
7.如图,小明想在自己家的窗口A处测量对面建筑物CD的高度,他首先量出窗口A到地面的距离为AB=1.5 m,又测得从A处看建筑物底部C的俯角为30°,看建筑物顶部D的仰角为45°,且AB,CD都与地面垂直,点A,B,C,D在同一平面内,则建筑物CD的高度为 米.
8.【2023·南昌月考】图1是一台实物投影仪,图2是它的示意图,折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面,经测量:AO=6.8 cm,CD=8 cm,AB=30 cm,BC=35 cm.如图2,∠ABC=70°,BC∥OE.则投影探头的端点D到桌面OE的距离为 cm.如图3,将图2中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6 cm时,则∠ABC的大小为 度.(参考数据:sin 70°≈0.94,cos 20°≈0.94,sin 36.8°≈0.60,cos 53.2°≈0.60)
9.【2023·唐山月考】如图,这是某型号机器人示意图,OA是垂直于工作台的移动基座,AB,BC为机械臂,OA=1 m,AB=5 m,BC=2 m,∠ABC=143°,机械臂端点C到工作台的距离CD=6 m.
(1)∠ABC的补角度数是 °.
(2)点A到直线BC的距离约是 m.
(3)OD的长约是 m.(结果精确到0.1 m)
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈2.24)
10.黑龙江亚布力地区的滑雪场在国内享誉盛名,如图,这是该地区某滑雪场的一段赛道示意图,AB段为助滑段,长为12米,坡角α为16°,一个曲面平台BCD连接了助滑坡AB与着陆坡DE.已知着陆坡DE的坡度i=1∶2.4,DE的长度为19.5米,B,D之间的垂直距离h为5.5米,则一人从A出发到E处下降的垂直距离约为 米.(参考数据:sin 16°≈0.28,cos 16°≈0.96,tan 16°≈0.29,结果保留一位小数)
三、解答题(本大题共2小题,满分20分)
11.(10分)如图,在△ABC中,BD⊥AC,AB=4,AC=3,∠A=30°.
(1)求AD的长.
(2)求sin C的值.
12.(10分)2022年11月29日,“神舟十五号”载人航天飞船搭载“明星”机械臂成功发射.2023年2月9日“神舟十五号”航天员进行了出舱活动,为了确保任务的圆满完成,航天员借助机械臂进行舱外作业.如图,这是处于工作状态的某型号手臂机器人示意图,OA是垂直于工作台的移动基座,AB,BC为机械臂,OA=1 m,AB=5 m,BC=2 m,∠ABC=145°,∠BCD=60°.
(1)求机械臂端点C到工作台的距离CD的长.(结果精确到0.1 m)
(2)求OD的长.(结果精确到0.1 m)
(参考数据:sin 25°≈0.42,cos 25°≈0.91,tan 25°≈0.47,≈1.41,≈1.73)
参考答案
1.C
2.C 【解析】当观测车从B点行驶到目标A的正下方的过程中,仰角逐渐增大,
行驶到目标A的正下方时,仰角最大,为90°,再继续行驶到C点的过程中,仰角逐渐减小.
故选C.
3.B
4.A 【解析】
如图,作OC⊥AB交AB于点C,
∵OA=OB,
∴OC平分∠AOB,点C平分AB.
∵∠AOB=2θ,
∴∠AOC=θ.
∵OA=OB=a,
∴AC=asin θ,
∴AB=2AC=2asin θ.
故选A.
5.B 【解析】
如图,过点O作EF⊥OM,过A作AG⊥EF于点G,
∵AB=6米,OA∶OB=2∶1,
∴OA=4米.
∵∠AOM=120°,∠EOM=90°,
∴∠AOE=30°.
在Rt△AOG中,AG=AO·sin 30°=2(米),
点A位于最高点时到地面的距离为2+3=5(米),
所以点A到地面的距离为5米.
故选B.
6.等边三角形 7.
8.27 33.2 【解析】过点A作AF⊥BC于点F,如图1,
则AF=AB·sin∠ABF=30·sin 70°≈28.2(cm),
∴投影探头的端点D到桌面OE的距离为AF+OA-CD=28.2+6.8-8=27(cm).
过点D作DH⊥OE于点H,过点B作BM⊥CD,与DC延长线相交于点M,过点A作AF⊥BM于点F,如图2,
则∠MBA=70°,
∴CM=AF+AO-DH-CD=28.2+6.8-6-8=21(cm),
∴sin∠MBC===0.6,
∴∠MBC=36.8°,
∴∠ABC=∠ABM-∠MBC=33.2°.
故答案为27;33.2.
9.(1)37 (2)3.0 (3)4.5
【解析】(1)∵∠ABC=143°,
∴∠ABC的补角是180°-143°=37°.
(2)如图,过点A作AE⊥BC交CB的延长线于点E,
在Rt△ABE中,
∴sin∠ABE=,
∴AE=AB·sin 37°≈3.0(m).
(3)如图,连接AC,过点A作AF⊥CD于点F,
∴四边形AFDO是矩形,
∴AF=DO,DF=OA=1(m),
∴CF=5(m).
在Rt△ABE中,
由勾股定理可知,BE==4(m),
∴CE=CB+BE=6(m).
在Rt△CEA中,
由勾股定理可知,AC2=32+62=45,
在Rt△ACF中,
由勾股定理可知,AF2=45-25=20,
∴AF=2≈4.5(m),
即OD≈4.5(m).
故答案为(1)37.
(2)3.0.
(3)4.5.
10.16.4 【解析】
如图,作BF⊥AP于点F,DG⊥AP于点G,DH⊥PE于点H,易知FG=h,GP=DH.在Rt△AFB中,sin 16°=,AB=12米,
∴AF=AB·sin 16°≈12×0.28=3.36(米).
设DH=x米,∵着陆坡DE的坡度i=1∶2.4,∴HE=2.4x,由勾股定理得,HE2+DH2=DE2,即(2.4x)2+x2=19.52,解得x=7.5,即DH=7.5(米).
∴一人从A出发到E处下降的垂直距离为AF+h+DH=3.36+5.5+7.5≈16.4(米).
11.【解析】(1)在Rt△ABD中,∠ADB=90°,AB=4,∠A=30°,
∴AD=AB·cos 30°=4×=2.
(2)∵AC=3,AD=2,
∴CD=AC-AD=.
∵∠ADB=90°,AB=4,∠A=30°,
∴BD=AB=2.
在Rt△CBD中,∠CDB=90°,BD=2,CD=,
∴BC==.
∴sin C===.
12.【解析】(1)如图,过点B作BE⊥CD于点E,过点B作BF⊥OD于点F,过点A作AG⊥BF于点G,
∴四边形BEDF是矩形,四边形AOFG是矩形,
∴BE=DF,BF=ED,∠EBF=90°,OA=GF=1米.
∵∠ABC=145°,∠BCD=60°,
∴∠CBE=30°,∠ABG=25°.
∵BC=2米,
∴CE=1米.
在Rt△ABG中,cos∠ABG=,
∴BG≈5×0.91≈4.6米,
∴BF=BG+GF=5.6米,
∴CD=CE+BF=1+5.6=6.6米.
答:机械臂端点C到工作台的距离CD的长6.6米.
(2)在Rt△BCE中,由勾股定理可知:BE=米,
在Rt△ABG中,
由勾股定理可知:AG=≈2.1米,
∴OF=AG≈2.1米,
∴OD=DF+OF≈3.8米.
答:OD的长为3.8米.
2
