2023-2024学年数学人教版九年级下册第二十九章 投影与视图 分层练习(含解析)
文档属性
| 名称 | 2023-2024学年数学人教版九年级下册第二十九章 投影与视图 分层练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 302.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 00:00:00 | ||
图片预览


文档简介
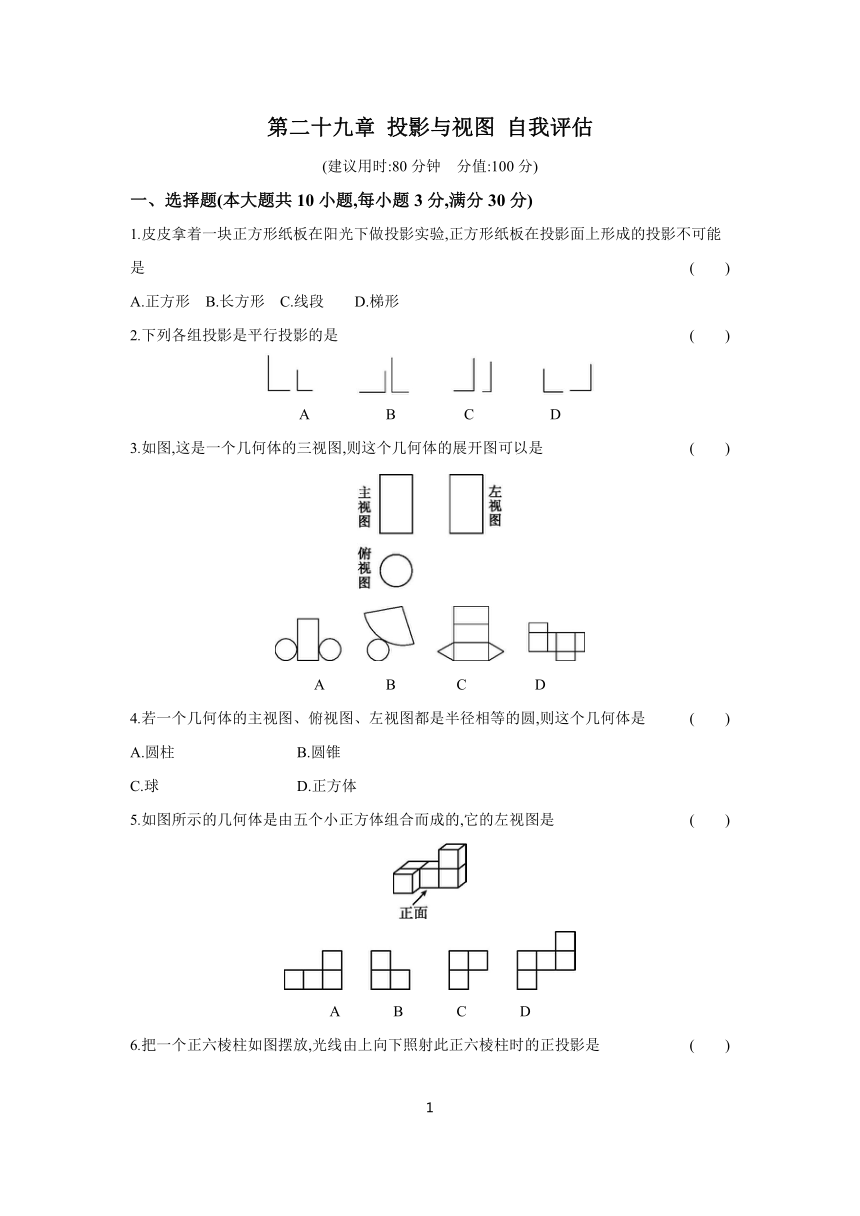
第二十九章 投影与视图 自我评估
(建议用时:80分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.皮皮拿着一块正方形纸板在阳光下做投影实验,正方形纸板在投影面上形成的投影不可能是 ( )
A.正方形 B.长方形 C.线段 D.梯形
2.下列各组投影是平行投影的是 ( )
A B C D
3.如图,这是一个几何体的三视图,则这个几何体的展开图可以是 ( )
A B C D
4.若一个几何体的主视图、俯视图、左视图都是半径相等的圆,则这个几何体是 ( )
A.圆柱 B.圆锥
C.球 D.正方体
5.如图所示的几何体是由五个小正方体组合而成的,它的左视图是 ( )
A B C D
6.把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是 ( )
A B C D
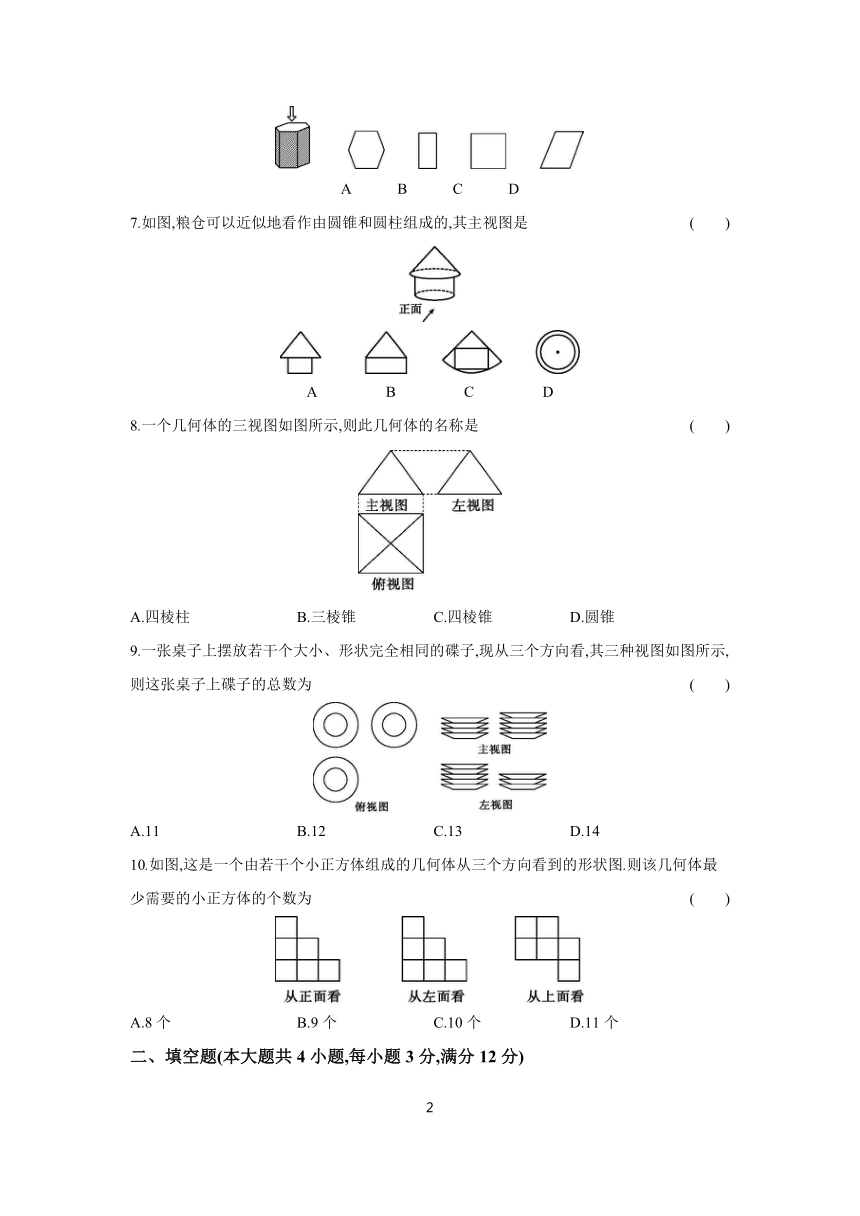
7.如图,粮仓可以近似地看作由圆锥和圆柱组成的,其主视图是 ( )
A B C D
8.一个几何体的三视图如图所示,则此几何体的名称是 ( )
A.四棱柱 B.三棱锥 C.四棱锥 D.圆锥
9.一张桌子上摆放若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为 ( )
A.11 B.12 C.13 D.14
10.如图,这是一个由若干个小正方体组成的几何体从三个方向看到的形状图.则该几何体最少需要的小正方体的个数为 ( )
A.8个 B.9个 C.10个 D.11个
二、填空题(本大题共4小题,每小题3分,满分12分)
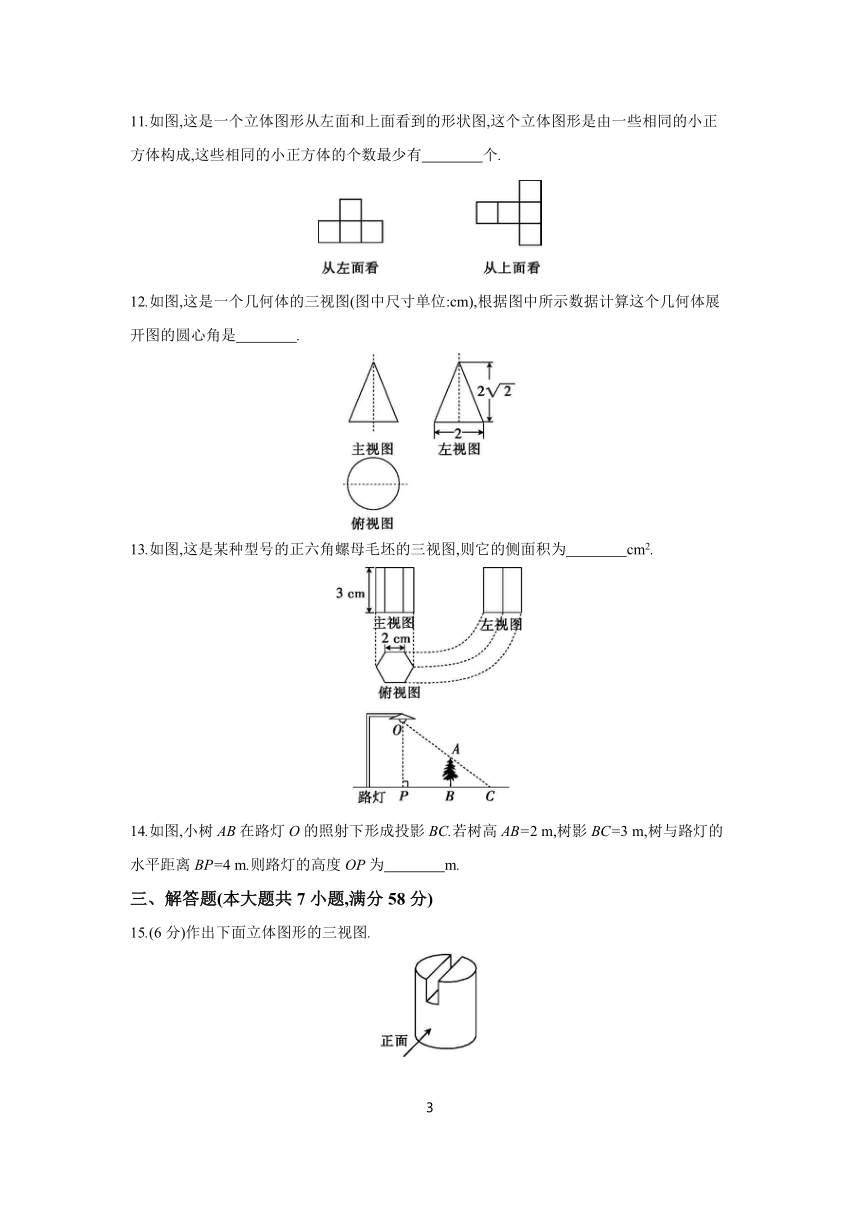
11.如图,这是一个立体图形从左面和上面看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数最少有 个.
12.如图,这是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体展开图的圆心角是 .
13.如图,这是某种型号的正六角螺母毛坯的三视图,则它的侧面积为 cm2.
14.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2 m,树影BC=3 m,树与路灯的水平距离BP=4 m.则路灯的高度OP为 m.
三、解答题(本大题共7小题,满分58分)
15.(6分)作出下面立体图形的三视图.
16.(6分)如图,这是一几何体从正面和从上面看到的形状图.(单位:cm)
(1)这个几何体的名称为 .
(2)画出它的一种表面展开图.
(3)若从正面看到的是长为10 cm,宽为6 cm的长方形,从上面看到的是三条边长均为6 cm的三角形(如图所示),求这个几何体的侧面积和所有棱长的和.
17.(8分)如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的.
(2)试计算出电线杆的高度,并写出计算的过程.
18.(9分)如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,求小方行走的路程.
19.(9分)为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索实践:根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把镜子放在离树AB有8.7米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者身高CD=1.6米,请你计算树AB的高度.(精确到0.1米)
20.(10分)图1所示的一个上面无盖的正方体纸盒,现将其剪开展成平面(如图2),已知展开图中每个正方形的边长为1.
(1)求在该展开图中可画出最长线段的长度,这样的线段可画几条
(2)试比较立体图中∠BAC与平面展开图中∠B'A'C'的大小关系.
21.(10分)如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处.小明测得窗户距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
参考答案
1.D 2.A 3.A 4.C 5.B 6.A 7.A 8.C 9.B
10.B 11.6 12.120°
13.36 【解析】这个正六角螺母的侧面积为6×S长方形=6×3×2=36( cm2).
故答案为36.
14.
15.【解析】
16.【解析】(1)三棱柱.
(2)答案不唯一,如:
(3)这个几何体的侧面积为3×6×10=180(cm2),
所有棱长的和为6×3×2+10×3=66(cm).
17.【解析】(1)平行.
(2)如图,过点E作EM⊥AB于点M,过点G作GN⊥CD于点N,
则MB=EF=2,ND=GH=3,ME=BF=10,NG=DH=5,
∴AM=10-2=8.
由平行投影可知,=,即=,
解得CD=7,即电线杆的高度为7米.
18.【解析】∵AE⊥OD,GO⊥OD,∴EA∥GO,
∴△AEB∽△OGB,
∴=,∴=,解得AB=2米.
∵OA所在的直线行走到点C时,人影长度增长3米,
∴DC=2+3=5米,
同理可得△DFC∽△DGO,∴=,
即=,解得AC=7.5米.
答:小方行走的路程AC为7.5米.
19.【解析】由题意知 ∠CED=∠AEB,∠CDE=∠ABE=90°,
∴△CED∽△AEB,∴=,
∴=,∴AB≈5.2米.
答:树AB的高度约为5.2米
20.【解析】(1)最长线段的长度为,这样的线段可画4条.
(2)如图,在平面展开图中,连接B'C',
由勾股定理可得A'B'=,B'C'=.
∵A'B'2+B'C'2=A'C'2,A'B'=B'C',
∴△A'B'C'为等腰直角三角形,
∴∠B'A'C'=45°,
∴∠BAC=∠B'A'C'.
21.【解析】如图,连接CD.
∵DO⊥BF,∴∠DOE=90°.
∵OD=0.8 m,OE=0.8 m,
∴∠DEB=45°.
∵AB⊥BF,∴∠BAE=45°,∴AB=BE.
设AB=BE=x m,
∵AB⊥BF,CO⊥BF,∴AB∥CO,
易得△ABF∽△COF,∴=,
=,解得x=4.4.
答:围墙AB的高度是4.4 m.
2
(建议用时:80分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.皮皮拿着一块正方形纸板在阳光下做投影实验,正方形纸板在投影面上形成的投影不可能是 ( )
A.正方形 B.长方形 C.线段 D.梯形
2.下列各组投影是平行投影的是 ( )
A B C D
3.如图,这是一个几何体的三视图,则这个几何体的展开图可以是 ( )
A B C D
4.若一个几何体的主视图、俯视图、左视图都是半径相等的圆,则这个几何体是 ( )
A.圆柱 B.圆锥
C.球 D.正方体
5.如图所示的几何体是由五个小正方体组合而成的,它的左视图是 ( )
A B C D
6.把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是 ( )
A B C D
7.如图,粮仓可以近似地看作由圆锥和圆柱组成的,其主视图是 ( )
A B C D
8.一个几何体的三视图如图所示,则此几何体的名称是 ( )
A.四棱柱 B.三棱锥 C.四棱锥 D.圆锥
9.一张桌子上摆放若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为 ( )
A.11 B.12 C.13 D.14
10.如图,这是一个由若干个小正方体组成的几何体从三个方向看到的形状图.则该几何体最少需要的小正方体的个数为 ( )
A.8个 B.9个 C.10个 D.11个
二、填空题(本大题共4小题,每小题3分,满分12分)
11.如图,这是一个立体图形从左面和上面看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数最少有 个.
12.如图,这是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体展开图的圆心角是 .
13.如图,这是某种型号的正六角螺母毛坯的三视图,则它的侧面积为 cm2.
14.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2 m,树影BC=3 m,树与路灯的水平距离BP=4 m.则路灯的高度OP为 m.
三、解答题(本大题共7小题,满分58分)
15.(6分)作出下面立体图形的三视图.
16.(6分)如图,这是一几何体从正面和从上面看到的形状图.(单位:cm)
(1)这个几何体的名称为 .
(2)画出它的一种表面展开图.
(3)若从正面看到的是长为10 cm,宽为6 cm的长方形,从上面看到的是三条边长均为6 cm的三角形(如图所示),求这个几何体的侧面积和所有棱长的和.
17.(8分)如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的.
(2)试计算出电线杆的高度,并写出计算的过程.
18.(9分)如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,求小方行走的路程.
19.(9分)为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索实践:根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把镜子放在离树AB有8.7米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者身高CD=1.6米,请你计算树AB的高度.(精确到0.1米)
20.(10分)图1所示的一个上面无盖的正方体纸盒,现将其剪开展成平面(如图2),已知展开图中每个正方形的边长为1.
(1)求在该展开图中可画出最长线段的长度,这样的线段可画几条
(2)试比较立体图中∠BAC与平面展开图中∠B'A'C'的大小关系.
21.(10分)如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处.小明测得窗户距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
参考答案
1.D 2.A 3.A 4.C 5.B 6.A 7.A 8.C 9.B
10.B 11.6 12.120°
13.36 【解析】这个正六角螺母的侧面积为6×S长方形=6×3×2=36( cm2).
故答案为36.
14.
15.【解析】
16.【解析】(1)三棱柱.
(2)答案不唯一,如:
(3)这个几何体的侧面积为3×6×10=180(cm2),
所有棱长的和为6×3×2+10×3=66(cm).
17.【解析】(1)平行.
(2)如图,过点E作EM⊥AB于点M,过点G作GN⊥CD于点N,
则MB=EF=2,ND=GH=3,ME=BF=10,NG=DH=5,
∴AM=10-2=8.
由平行投影可知,=,即=,
解得CD=7,即电线杆的高度为7米.
18.【解析】∵AE⊥OD,GO⊥OD,∴EA∥GO,
∴△AEB∽△OGB,
∴=,∴=,解得AB=2米.
∵OA所在的直线行走到点C时,人影长度增长3米,
∴DC=2+3=5米,
同理可得△DFC∽△DGO,∴=,
即=,解得AC=7.5米.
答:小方行走的路程AC为7.5米.
19.【解析】由题意知 ∠CED=∠AEB,∠CDE=∠ABE=90°,
∴△CED∽△AEB,∴=,
∴=,∴AB≈5.2米.
答:树AB的高度约为5.2米
20.【解析】(1)最长线段的长度为,这样的线段可画4条.
(2)如图,在平面展开图中,连接B'C',
由勾股定理可得A'B'=,B'C'=.
∵A'B'2+B'C'2=A'C'2,A'B'=B'C',
∴△A'B'C'为等腰直角三角形,
∴∠B'A'C'=45°,
∴∠BAC=∠B'A'C'.
21.【解析】如图,连接CD.
∵DO⊥BF,∴∠DOE=90°.
∵OD=0.8 m,OE=0.8 m,
∴∠DEB=45°.
∵AB⊥BF,∴∠BAE=45°,∴AB=BE.
设AB=BE=x m,
∵AB⊥BF,CO⊥BF,∴AB∥CO,
易得△ABF∽△COF,∴=,
=,解得x=4.4.
答:围墙AB的高度是4.4 m.
2
