3.3正比例-2023-2024学年数学六年级下册同步培优讲义(冀教版)(含解析)
文档属性
| 名称 | 3.3正比例-2023-2024学年数学六年级下册同步培优讲义(冀教版)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 254.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 00:00:00 | ||
图片预览



文档简介
(讲义)3.3正比例(知识精讲+典题精练)
1.正比例
【知识点归纳】
正比例,简称正比,是指两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数比值(或者说商)一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
举例如下:
(1)同圆的周长与直径 (比值:π)。
(2)正方形的周长与边长 (比值:4)。
(3)速度一定,路程和时间成正比例;时间一定,路程和速度成正比例。
(4)购买的总价与购买的数量(比值:单价)。
解:aX=Y中,a不变,则 X与Y成正比例。一个变量随着另一个变量的变化而变化。
(5)易错题:圆的面积(S):半径(R)=πR
解:这个比例是错误的,它不属于正比例。因为(S:R=πR)因为根据上面所说,比值须是一个不变的量,而比的前项和后项必须是可以变化的量,如果R变化,那比值也会变化,所以圆的面积与半径不成正比例。
(6)圆的周长和半径成正比例吗?为什么?
解:因为圆的周长除以圆的半径=2π,所以圆的周长和半径成正比例。
(7)易错题:正方形的面积与边长中,S:A=A
解:由上述可以看出:比值是个变量,它不能与比的任意一项相同,所以这个比例也不是正比例。
但如果圆的面积(S):(R R) (R的平方)=π,这可看成一个正比例,它是S与(R R)成正比例。
↑一种量
(8)易错题:圆的面积(S):π=R R(一定)
解:这是一个错误的比例,因为比值是不变的量,前项与后项应随着一个的变化而变化,而在这里,比值是个固定的量,而π也是一个固定的量,前项无法变化,这个比例就成了一个固定的比例,不符合上面所说的前项和后项必须是可以变化的量。
(9)常见错误:长方形的周长一定,长和宽成正比例。
具体证明既可以用公式推导,2(a+b)=C,a+b=C/2(一定),发现长宽之和一定,而积不一定,故长和宽不成正比例。也可以用具体数据计算,比如周长为10厘米时,长9宽1积为9,长8宽2积为16,长7宽3积为21,长6宽4积为24,发现积不一定,故不成正比例。
一.选择题(共9小题)
1.( )中的两个量不成正比例。
A.在同一个正方形中,正方形的周长和边长
B.一箱苹果,吃掉的个数和剩下的个数
C.长方体的底面积一定,高和体积
D.订阅某期刊的份数一定,单价和总钱数
2.如图中,表示正比例图象的是( )
A. B. C. D.
3.圆的半径扩大4倍,这个圆的面积扩大( )
A.8 B.12 C.16
4.飞机飞行的速度一定,飞行的时间与航程( )
A.成正比例 B.成反比例 C.不成比例
5.买同样的书,花钱的总价与( )成正比例.
A.书的本数 B.书的页数 C.书的单价 D.不能确定
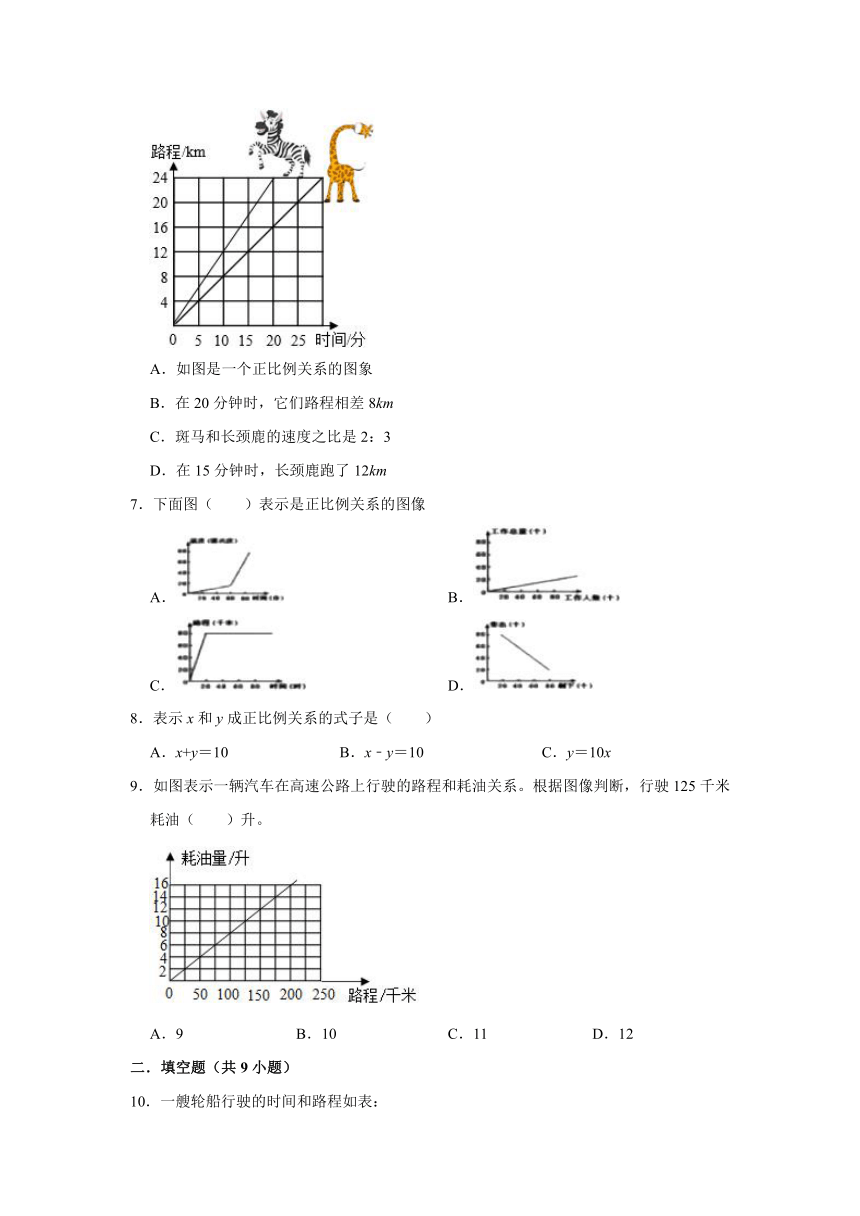
6.如图中表示斑马和长颈鹿的奔跑情况。下面叙述错误的是( )
A.如图是一个正比例关系的图象
B.在20分钟时,它们路程相差8km
C.斑马和长颈鹿的速度之比是2:3
D.在15分钟时,长颈鹿跑了12km
7.下面图( )表示是正比例关系的图像
A. B.
C. D.
8.表示x和y成正比例关系的式子是( )
A.x+y=10 B.x﹣y=10 C.y=10x
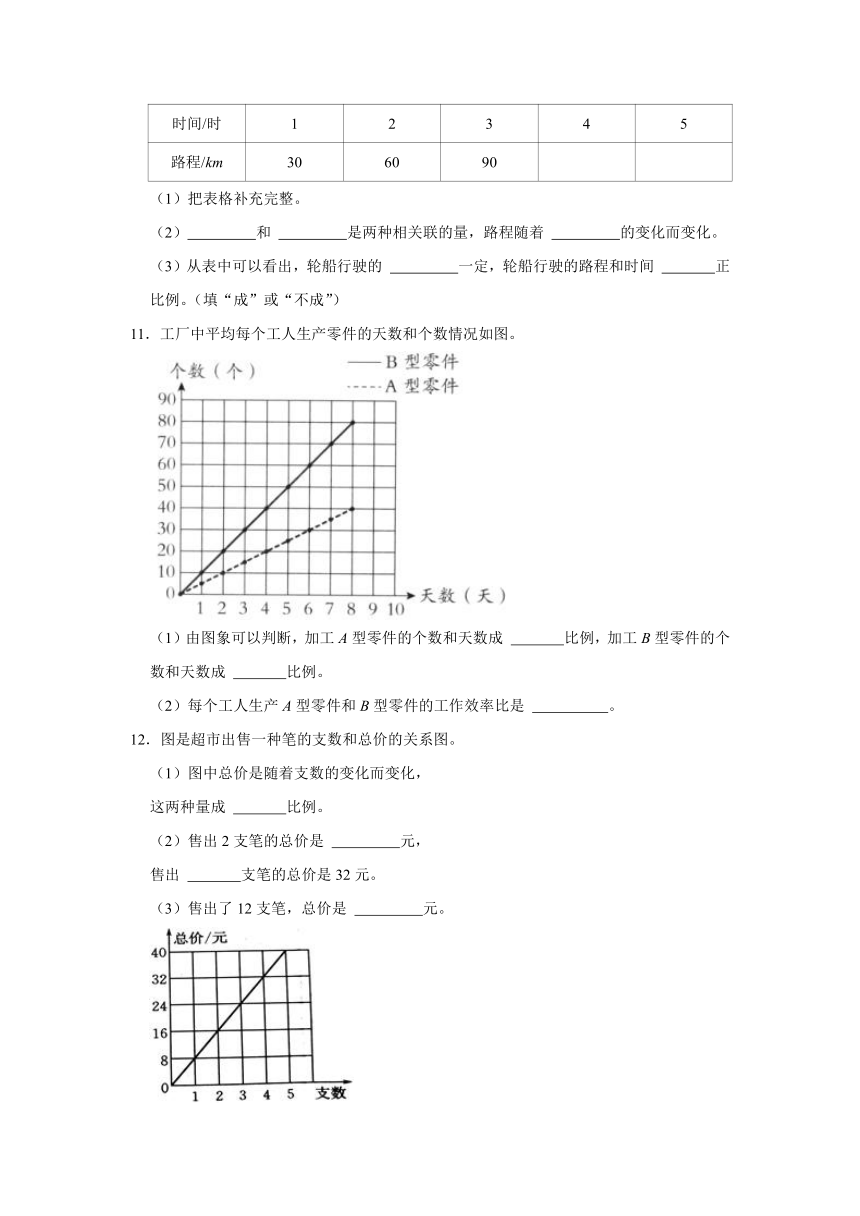
9.如图表示一辆汽车在高速公路上行驶的路程和耗油关系。根据图像判断,行驶125千米耗油( )升。
A.9 B.10 C.11 D.12
二.填空题(共9小题)
10.一艘轮船行驶的时间和路程如表:
时间/时 1 2 3 4 5
路程/km 30 60 90
(1)把表格补充完整。
(2) 和 是两种相关联的量,路程随着 的变化而变化。
(3)从表中可以看出,轮船行驶的 一定,轮船行驶的路程和时间 正比例。(填“成”或“不成”)
11.工厂中平均每个工人生产零件的天数和个数情况如图。
(1)由图象可以判断,加工A型零件的个数和天数成 比例,加工B型零件的个数和天数成 比例。
(2)每个工人生产A型零件和B型零件的工作效率比是 。
12.图是超市出售一种笔的支数和总价的关系图。
(1)图中总价是随着支数的变化而变化,
这两种量成 比例。
(2)售出2支笔的总价是 元,
售出 支笔的总价是32元。
(3)售出了12支笔,总价是 元。
13.路程和时间的比的比值是 ,如果它一定,那么路程和时间成 比例.
14.下面各图都有表示了x,y两种变量,表示的两种量成正比例的是 。
15.一辆汽车在公路上行驶的时间和路程如图。看图填写如表:
时间/小时 2
路程/千米 400
这辆汽车行驶的路程和时间成 比例。
16.乘船的人数与所付船费如下表。
人数/人 1 2 3 4
船费/元 5 10 15 20
(1)表格中的 和 是两种相关联的量,船费随着 的变化而变化;
(2)船费与人数数量中相对应的两个数的比值是 ,这个比值实际上表示 ;
(3)因为每人的 一定,所以 和 成 比例关系。
17.一辆汽车行驶的路程和时间的关系如图。
(1)点A表示汽车 时行驶了 km;行驶400km需要 时;2.5时行驶了 km。
(2)点(10,800) 这条直线上。(填“在”或“不在”)
(3)这辆汽车的速度是 千米/时。
18.若x与y成正比例,则m= ,若x与y成反比例,则m= 。
X 4 5
y 16 m
三.判断题(共10小题)
19.yx(x≠0),x和y成正比例. .
20.长方体的高一定,底面积和体积成正比例关系。
21.如果一个量变大,另一个量也变大,这两个量成正比例。
22.订阅《少年文艺》的份数与总钱数成反比例. .
23.每袋花生的质量一定,花生的总质量和袋数成正比。
24.成正比例的量,在坐标系中描出的点连接起来不是一条直线。
25.正比例的图象不一定是一条直线。
26.正方体的一个面的面积和它的表面积成 比例.
27.如果ab÷5=17,则a与b成正比例。
28.每本书的单价一定,本数和总价成正比例. .
四.应用题(共1小题)
29.书房的面积是16m2,刚好用了32块地砖,卧室的面积是20m2,用同样的地砖,需要多少块?
(讲义)3.3正比例(知识精讲+典题精练)-2023-2024学年数学六年级下册同步培优讲义(冀教版)
参考答案与试题解析
一.选择题(共9小题)
1.【答案】B
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
【解答】解:A项:边长=周长÷4(一定),比值一定,在同一个正方形中,正方形的周长和边长成正比例关系;
B项:一箱苹果的总个数﹣吃掉的个数=剩下的个数,比值和积都不一定,吃掉的个数和剩下的个数不成比例;
C项:长方体的体积÷高=底面积(一定),比值一定,高和体积成正比例关系;
D项:总价÷单价=数量(一定),比值一定,单价和总钱数成正比例关系。
故选:B。
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断。
2.【答案】B
【分析】根据正比例的意义是:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们之间的关系就是正比例关系,由此可知,正比例的图象是过原点的一条射线,据此解答。
【解答】解;根据正比例图象的特点可知,图B符合正比例图象的特点,所以图B是正比例图象。
故选:B。
【点评】此题考查的目的是理解掌握正比例的意义以及正比例图象的特点。
3.【答案】C
【分析】根据圆的面积公式,S=πr2,知道圆的半径的平方和圆的面积成正比例,由此即可得出答案.
【解答】解:因为,S=πr2,
所以,π(一定),
即,半径扩大4倍,面积扩大16倍;
故选:C。
【点评】解答此题的关键是,先根据圆的面积公式,判断圆的面积与半径的关系,再根据正比例的意义,即可得出答案.
4.【答案】A
【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系.
【解答】解:飞机飞行的时间与航程是两种相关联的量,航程随时间的变化而变化.飞机飞行的速度一定,也就是飞行的航程与时间的比值一定,所以飞机飞行的时间与航程成正比例关系.
故选:A。
【点评】此题考查正比例和反比例的意义.
5.【答案】A
【分析】根据总价=单价×数量的数量关系进行分析.要想知道总价与什么成正比例,就要找到一定的量和变化的量,根据正比例的意义,总价与变量相比才能成正比例.
【解答】解:买同样的书,也就是书的单价一定.可得:
总价:数量=单价(一定)
可以看出,总价和数量是两种相关联的量,总价随数量的变化而变化.单价一定,也就是总价与数量相对应数的比值一定.所以花钱的总价与数量(书的本数)成正比例关系.
故选:A。
【点评】此题重点考查正比例和反比例的意义.
6.【答案】C
【分析】由图可知:斑马和长颈鹿的奔跑的路程和时间的商一定,也就是速度一定,可以判断图象是正比例图象;从图像上可以看出,20分钟时,长颈鹿奔跑了16km,斑马奔跑了24km,两者相减,可得出它们的路程差;根据图像数据,分别计算出20分钟时斑马和长颈鹿的速度,再求速度比;从图像上可以看出,15分钟时,长颈鹿奔跑的路程是12km。
【解答】解:选项A中,斑马和长颈鹿的奔跑的路程和时间的商一定,奔跑的路程和时间成正比例。原题说法正确。
选项B中,20分钟时,长颈鹿奔跑了16km,斑马奔跑了24km,两者相差8km。原题说法正确。
选项C中,斑马的速度:24÷20=1.2(km/分)
长颈鹿的速度:16÷20=0.8(km/分)
1.2:0.8=3:2
原题说法错误。
选项D中,从图像上看出,在15分钟时,长颈鹿跑了12km。原题说法正确。
故选:C。
【点评】本题考查了对成正比例关系图象的认识。根据图象找出有用的信息进行计算是解答本题的关键。
7.【答案】B
【分析】成正比例关系的图像是一条经过原点的直线,据此判断。
【解答】解:选项A和选项C中的图像都不是直线,选项D虽然是直线,但图像没有经过原点,所以它们都不是成正比例关系的图像;选项B中的图像是一条过原点的直线,表示成正比例关系。
故选:B。
【点评】本题考查了成正比例关系的图像的认识,需明确成正比例关系的图像是一条经过原点的直线。
8.【答案】C
【分析】判断x与y是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.
【解答】解:A.x+y=10,x与y的和一定,不符合正比例的意义;
B.y﹣x=10,x与y的差一定,不符合正比例的意义;
C.由y=10x得,所以x、y比值一定,x与y成正比例,符合题意;
故选:C.
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断.
9.【答案】见试题解答内容
【分析】从图象中找到路程为125千米的点,看它对应的耗油量。
【解答】解:路程125千米,从图像上看耗油量是10升。
故选:B。
【点评】此题重点考查从折线统计图中读取信息进行分析。
二.填空题(共9小题)
10.【答案】(1)120,150;(2)路程,时间,时间;(3)速度,成。
【分析】根据路程÷时间=速度=30(一定),所以路程和时间是两个相关联的量,路程是随着时间的变化而变化的。这两个量中相对应的两个数的比值一定,这两个量就叫做成正比例的量,它们的关系叫做正比例的关系。
【解答】解:(1)4×30﹣120(km)
5×30=150(km)
时间/时 1 2 3 4 5
路程/km 30 60 90 120 150
(2)路程和时间是两种相关联的量,路程随着时间的变化而变化。
(3)从表中可以看出,轮船行驶的速度一定,轮船行驶的路程和时间成正比例。
故答案为:120,150;路程,时间,时间;速度,成。
【点评】此题主要考查对正比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的相对应的比值一定,这两种量成正比例。
11.【答案】(1)正;正;(2)1:2。
【分析】(1)由图象可以得到零件的个数与天数的比例关系;
(2)由天数为1天时对应的个数为5和10,即可解答题目。
【解答】解:(1)由图象可以判断,加工A型零件的个数和天数成正比例,加工B型零件的个数和天数成正比例。
(2)5:10=1:2
答:每个工人生产A型零件和B型零件的工作效率比是1:2。
故答案为:正;正;1:2。
【点评】本题考查正比例的认识,熟练掌握正比例的意义是解题的关键。
12.【答案】(1)正。
(2)16,4。
(3)96。
【分析】(1)图像是一条直线,所以总价和支数成正比例关系。
(2)从图像中可以看出,每支笔的单价为8元,根据总价=单价×数量、数量=总价÷单价解答。
(3)根据总价=单价×数量解答。
【解答】解:(1)图中总价是随着支数的变化而变化,这两种量成正比例。
(2)8×2=16(元)
32÷8=4(支)
答:售出2支笔的总价是16元,售出4支笔的总价是32元。
(3)8×12=96(元)
答:售出了12支笔,总价是96元。
故答案为:正;16,4;96。
【点评】本题考查了根据比例图像解决问题,能根据图像分析数量关系是关键。
13.【答案】见试题解答内容
【分析】根据路程、时间和速度的关系,求出路程和时间的比的比值即速度,如果速度一定,也就是比值一定,路程和时间就成正比例.
【解答】解:路程:时间=速度(一定),也就是比值一定,路程和时间就成正比例.
故答案为:速度,正.
【点评】解决关键是先求出路程和时间的比的比值,再根据比值一定,判断路程和时间成正比例.
14.【答案】②。
【分析】从三幅图中找出几组对应的x与y,并求出它们的商;根据如果商一定就成正比例,据此计算即可解答题目。
【解答】解:A:4÷2=2,16÷4=4,则两种量的比值是不一定的,所以不成正比例的关系;
B:4÷1=4,8÷2=4,则图中的两种量的比值是一定的,都是4,所以成正比例的关系;
C:2÷6,4÷4=1,则两种量的比值是不一定的,所以不成正比例的关系。
故答案为:②。
【点评】本题是一道关于正比例方面的题目,可依据判断正比例的方法以及正比例的意义求解。
15.【答案】200;4;正。
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【解答】解:
时间/小时 2 4
路程/千米 200 400
这辆汽车行驶的路程和时间成正比例。
故答案为:200;4;正。
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断。
16.【答案】(1)船费,人数,人数;(2)5,每人所付的船费;(3)所付船费,船费,人数,正。
【分析】(1)上表中,表格中的船费和人数是两种相关联的量,船费随着人数的变化而变化;
(2)求船费与人数数量中相对应的两个数的比值,用船费:人数=每人所付的船费,所以这个比值表示每人所付的船费;
(3)因为船费:人数=每人所付的船费,每人所付船费一定,所以船费和人数成正比例关系;据此解答。
【解答】解:(1)表格中的船费和人数是两种相关联的量,船费随着人数的变化而变化;
(2)5:1=10:2
答:船费与人数数量中相对应的两个数的比值是5,这个比值实际上表示每人所付的船费;
(3)因为每人的所付船费一定,所以船费和人数成正比例关系。
故答案为:船费,人数,人数;5,每人所付的船费;所付船费,船费,人数,正。
【点评】此题主要考查正比例的意义以及总价、数量和单价之间的关系,正比例的意义是:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量。
17.【答案】(1)1,80,5,200;(2)在;(3)80。
【分析】(1)图中直观显示,点A表示汽车1时行驶了80km;行驶400km需要5时;2.5时行驶了200km。
(2)从图上可知汽车1时行驶了80km,点中10表示10时,求出汽车10时行驶的路程,与800比较即可。
(3)根据速度=路程÷时间可求得。
【解答】解:(1)80×2.5=200(km)
点A表示汽车1时行驶了80km;行驶400km需要5时;2.5时行驶了200km。
(2)80×10=800(km)
答:点(10,800)在这条直线上。
(3)160÷2=80(千米/时)
答:这辆汽车的速度是80千米/时。
故答案为:1,80,5,200;在;80。
【点评】此题考查了正比例关系的图象的应用,利用数形结合的思想解决问题是常用的一种数学思想方法。
18.【答案】20,12.8
【分析】(1)如果x与y成正比例,由正比例的意义可得4:16=5:m,把m看作未知数,根据比例的基本性质进行解比例即可;
(2)如果x和y成反比例,由反比例的意义可得5×m=4×16,把m看作未知数,根据等式的性质进行解方程即可。
【解答】解:根据题意可得:
(1)4:16=5:m
4m=16×5
4m=80
4m÷4=80÷4
m=20
所以,如果x与y成正比例,“m”是20;
(2)5×m=4×16
5m=64
5m÷5=64÷5
m=12.8
所以,如果x和y成反比例,“m”是12.8。
故答案为:20,12.8
【点评】本题主要考查正反比例的意义,然后根据题意列出比例或方程再进一步解答即可.
三.判断题(共10小题)
19.【答案】见试题解答内容
【分析】要想判定x和y成不成正比例关系,必须根据式子,进行推导.再根据正比例的意义,分析数量关系,找出一定的量,看看x和y是不是比值一定.
【解答】解:因为 yx(x≠0),
所以 y:x(一定),
可以看出,y和x是两个相关联的变化的量,它们相对应的数的比值是,是一定的,所以y和x成正比例关系.
故答案为:√.
【点评】此题重点考查正比例的意义.
20.【答案】√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:长方体的体积=底面积×高,高=长方体的体积÷底面积。长方体的高一定,所以它的体积和底面积成正比例关系,原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
21.【答案】×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:如果一个量变大,另一个量也变大,但比值不一定,所以这两量不成正比例,所以原题说法错误。
故答案为:×。
【点评】此题考查了判断两个相关联的量之间成什么比例的方法。
22.【答案】见试题解答内容
【分析】订阅《少年文艺》的份数与总钱数是两种相关联的量,总钱数÷份数=每份的钱数,每份的钱数,即单价一定,也就是这两种量的比值一定,所以成正比例,不成反比例.
【解答】解:总钱数÷份数=每份的钱数,
每份的钱数,即单价一定,也就是这两种量的比值一定,所以成正比例;
故答案为:×.
【点评】此题考查辨识成正比例的量,只要两种相关联的量比值一定,就成正比例.
23.【答案】√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:因为花生的总质量:袋数=每袋的质量(一定),是比值一定,所以花生的总质量和袋数成正比例,所以原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
24.【答案】×
【分析】成正比例的两个量的比值一定,所以是一条直线。
【解答】解:成正比例的两个量的比值一定,所以是一条直线。
故答案为;×。
【点评】本题考查了学生对成正比例的两个量的关系的理解。
25.【答案】×
【分析】两种相关联的量中相对应的两个数的商一定,就成正比例关系,正比例的图象是一条过原点的直线。
【解答】解:两种相关联的量中相对应的两个数的商一定,就成正比例关系,正比例的图象是一条过原点的直线。所以原题干错误。
故答案为:×。
【点评】本题考查的是正比例的意义,熟知正比例函数的图象是经过原点的一条直线是解答此题的关键。
26.【答案】见试题解答内容
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例.
【解答】解:正方体的表面积÷一个面的面积=6(一定),是比值一定,所以正方体的一个面的面积和它的表面积成正比例;
故答案为:正.
【点评】此题属于根据正、反比例的意义,判断两种相关联的量是成正比例还是成反比例,就看两种量是对应的比值一定,还是对应的乘积一定,再做出解答.
27.【答案】×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此分析。
【解答】解:如果ab÷5=17,ab=17×5=85(一定),是两个量的乘积一定,则a与b成反比例;原题说法错误。
故答案为:×。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
28.【答案】见试题解答内容
【分析】判断本数和总价是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果是比值不一定,就不成正比例.
【解答】解:总价÷本数=每本书的单价(一定),是比值一定,本数和总价就成正比例.
故判断为:正确.
【点评】此题属于辨识成正比例的量,就看这两种量是否是对应的比值一定,再做出判断.
四.应用题(共1小题)
29.【答案】40块。
【分析】根据题意知道,地砖的面积一定,房子的面积÷地砖的块数=地砖的面积(一定),所以房子的面积与方砖的块数成正比例,由此列出比例解答即可。
【解答】解:设用同样的地砖,需要X块。
16:32=20:X
16X=640
X=40
答:用同样的地砖,需要40块。
【点评】关键是判断出房子的面积与方砖的块数成正比例,由此解决问题。
1.正比例
【知识点归纳】
正比例,简称正比,是指两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数比值(或者说商)一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
举例如下:
(1)同圆的周长与直径 (比值:π)。
(2)正方形的周长与边长 (比值:4)。
(3)速度一定,路程和时间成正比例;时间一定,路程和速度成正比例。
(4)购买的总价与购买的数量(比值:单价)。
解:aX=Y中,a不变,则 X与Y成正比例。一个变量随着另一个变量的变化而变化。
(5)易错题:圆的面积(S):半径(R)=πR
解:这个比例是错误的,它不属于正比例。因为(S:R=πR)因为根据上面所说,比值须是一个不变的量,而比的前项和后项必须是可以变化的量,如果R变化,那比值也会变化,所以圆的面积与半径不成正比例。
(6)圆的周长和半径成正比例吗?为什么?
解:因为圆的周长除以圆的半径=2π,所以圆的周长和半径成正比例。
(7)易错题:正方形的面积与边长中,S:A=A
解:由上述可以看出:比值是个变量,它不能与比的任意一项相同,所以这个比例也不是正比例。
但如果圆的面积(S):(R R) (R的平方)=π,这可看成一个正比例,它是S与(R R)成正比例。
↑一种量
(8)易错题:圆的面积(S):π=R R(一定)
解:这是一个错误的比例,因为比值是不变的量,前项与后项应随着一个的变化而变化,而在这里,比值是个固定的量,而π也是一个固定的量,前项无法变化,这个比例就成了一个固定的比例,不符合上面所说的前项和后项必须是可以变化的量。
(9)常见错误:长方形的周长一定,长和宽成正比例。
具体证明既可以用公式推导,2(a+b)=C,a+b=C/2(一定),发现长宽之和一定,而积不一定,故长和宽不成正比例。也可以用具体数据计算,比如周长为10厘米时,长9宽1积为9,长8宽2积为16,长7宽3积为21,长6宽4积为24,发现积不一定,故不成正比例。
一.选择题(共9小题)
1.( )中的两个量不成正比例。
A.在同一个正方形中,正方形的周长和边长
B.一箱苹果,吃掉的个数和剩下的个数
C.长方体的底面积一定,高和体积
D.订阅某期刊的份数一定,单价和总钱数
2.如图中,表示正比例图象的是( )
A. B. C. D.
3.圆的半径扩大4倍,这个圆的面积扩大( )
A.8 B.12 C.16
4.飞机飞行的速度一定,飞行的时间与航程( )
A.成正比例 B.成反比例 C.不成比例
5.买同样的书,花钱的总价与( )成正比例.
A.书的本数 B.书的页数 C.书的单价 D.不能确定
6.如图中表示斑马和长颈鹿的奔跑情况。下面叙述错误的是( )
A.如图是一个正比例关系的图象
B.在20分钟时,它们路程相差8km
C.斑马和长颈鹿的速度之比是2:3
D.在15分钟时,长颈鹿跑了12km
7.下面图( )表示是正比例关系的图像
A. B.
C. D.
8.表示x和y成正比例关系的式子是( )
A.x+y=10 B.x﹣y=10 C.y=10x
9.如图表示一辆汽车在高速公路上行驶的路程和耗油关系。根据图像判断,行驶125千米耗油( )升。
A.9 B.10 C.11 D.12
二.填空题(共9小题)
10.一艘轮船行驶的时间和路程如表:
时间/时 1 2 3 4 5
路程/km 30 60 90
(1)把表格补充完整。
(2) 和 是两种相关联的量,路程随着 的变化而变化。
(3)从表中可以看出,轮船行驶的 一定,轮船行驶的路程和时间 正比例。(填“成”或“不成”)
11.工厂中平均每个工人生产零件的天数和个数情况如图。
(1)由图象可以判断,加工A型零件的个数和天数成 比例,加工B型零件的个数和天数成 比例。
(2)每个工人生产A型零件和B型零件的工作效率比是 。
12.图是超市出售一种笔的支数和总价的关系图。
(1)图中总价是随着支数的变化而变化,
这两种量成 比例。
(2)售出2支笔的总价是 元,
售出 支笔的总价是32元。
(3)售出了12支笔,总价是 元。
13.路程和时间的比的比值是 ,如果它一定,那么路程和时间成 比例.
14.下面各图都有表示了x,y两种变量,表示的两种量成正比例的是 。
15.一辆汽车在公路上行驶的时间和路程如图。看图填写如表:
时间/小时 2
路程/千米 400
这辆汽车行驶的路程和时间成 比例。
16.乘船的人数与所付船费如下表。
人数/人 1 2 3 4
船费/元 5 10 15 20
(1)表格中的 和 是两种相关联的量,船费随着 的变化而变化;
(2)船费与人数数量中相对应的两个数的比值是 ,这个比值实际上表示 ;
(3)因为每人的 一定,所以 和 成 比例关系。
17.一辆汽车行驶的路程和时间的关系如图。
(1)点A表示汽车 时行驶了 km;行驶400km需要 时;2.5时行驶了 km。
(2)点(10,800) 这条直线上。(填“在”或“不在”)
(3)这辆汽车的速度是 千米/时。
18.若x与y成正比例,则m= ,若x与y成反比例,则m= 。
X 4 5
y 16 m
三.判断题(共10小题)
19.yx(x≠0),x和y成正比例. .
20.长方体的高一定,底面积和体积成正比例关系。
21.如果一个量变大,另一个量也变大,这两个量成正比例。
22.订阅《少年文艺》的份数与总钱数成反比例. .
23.每袋花生的质量一定,花生的总质量和袋数成正比。
24.成正比例的量,在坐标系中描出的点连接起来不是一条直线。
25.正比例的图象不一定是一条直线。
26.正方体的一个面的面积和它的表面积成 比例.
27.如果ab÷5=17,则a与b成正比例。
28.每本书的单价一定,本数和总价成正比例. .
四.应用题(共1小题)
29.书房的面积是16m2,刚好用了32块地砖,卧室的面积是20m2,用同样的地砖,需要多少块?
(讲义)3.3正比例(知识精讲+典题精练)-2023-2024学年数学六年级下册同步培优讲义(冀教版)
参考答案与试题解析
一.选择题(共9小题)
1.【答案】B
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
【解答】解:A项:边长=周长÷4(一定),比值一定,在同一个正方形中,正方形的周长和边长成正比例关系;
B项:一箱苹果的总个数﹣吃掉的个数=剩下的个数,比值和积都不一定,吃掉的个数和剩下的个数不成比例;
C项:长方体的体积÷高=底面积(一定),比值一定,高和体积成正比例关系;
D项:总价÷单价=数量(一定),比值一定,单价和总钱数成正比例关系。
故选:B。
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断。
2.【答案】B
【分析】根据正比例的意义是:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们之间的关系就是正比例关系,由此可知,正比例的图象是过原点的一条射线,据此解答。
【解答】解;根据正比例图象的特点可知,图B符合正比例图象的特点,所以图B是正比例图象。
故选:B。
【点评】此题考查的目的是理解掌握正比例的意义以及正比例图象的特点。
3.【答案】C
【分析】根据圆的面积公式,S=πr2,知道圆的半径的平方和圆的面积成正比例,由此即可得出答案.
【解答】解:因为,S=πr2,
所以,π(一定),
即,半径扩大4倍,面积扩大16倍;
故选:C。
【点评】解答此题的关键是,先根据圆的面积公式,判断圆的面积与半径的关系,再根据正比例的意义,即可得出答案.
4.【答案】A
【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系.
【解答】解:飞机飞行的时间与航程是两种相关联的量,航程随时间的变化而变化.飞机飞行的速度一定,也就是飞行的航程与时间的比值一定,所以飞机飞行的时间与航程成正比例关系.
故选:A。
【点评】此题考查正比例和反比例的意义.
5.【答案】A
【分析】根据总价=单价×数量的数量关系进行分析.要想知道总价与什么成正比例,就要找到一定的量和变化的量,根据正比例的意义,总价与变量相比才能成正比例.
【解答】解:买同样的书,也就是书的单价一定.可得:
总价:数量=单价(一定)
可以看出,总价和数量是两种相关联的量,总价随数量的变化而变化.单价一定,也就是总价与数量相对应数的比值一定.所以花钱的总价与数量(书的本数)成正比例关系.
故选:A。
【点评】此题重点考查正比例和反比例的意义.
6.【答案】C
【分析】由图可知:斑马和长颈鹿的奔跑的路程和时间的商一定,也就是速度一定,可以判断图象是正比例图象;从图像上可以看出,20分钟时,长颈鹿奔跑了16km,斑马奔跑了24km,两者相减,可得出它们的路程差;根据图像数据,分别计算出20分钟时斑马和长颈鹿的速度,再求速度比;从图像上可以看出,15分钟时,长颈鹿奔跑的路程是12km。
【解答】解:选项A中,斑马和长颈鹿的奔跑的路程和时间的商一定,奔跑的路程和时间成正比例。原题说法正确。
选项B中,20分钟时,长颈鹿奔跑了16km,斑马奔跑了24km,两者相差8km。原题说法正确。
选项C中,斑马的速度:24÷20=1.2(km/分)
长颈鹿的速度:16÷20=0.8(km/分)
1.2:0.8=3:2
原题说法错误。
选项D中,从图像上看出,在15分钟时,长颈鹿跑了12km。原题说法正确。
故选:C。
【点评】本题考查了对成正比例关系图象的认识。根据图象找出有用的信息进行计算是解答本题的关键。
7.【答案】B
【分析】成正比例关系的图像是一条经过原点的直线,据此判断。
【解答】解:选项A和选项C中的图像都不是直线,选项D虽然是直线,但图像没有经过原点,所以它们都不是成正比例关系的图像;选项B中的图像是一条过原点的直线,表示成正比例关系。
故选:B。
【点评】本题考查了成正比例关系的图像的认识,需明确成正比例关系的图像是一条经过原点的直线。
8.【答案】C
【分析】判断x与y是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.
【解答】解:A.x+y=10,x与y的和一定,不符合正比例的意义;
B.y﹣x=10,x与y的差一定,不符合正比例的意义;
C.由y=10x得,所以x、y比值一定,x与y成正比例,符合题意;
故选:C.
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断.
9.【答案】见试题解答内容
【分析】从图象中找到路程为125千米的点,看它对应的耗油量。
【解答】解:路程125千米,从图像上看耗油量是10升。
故选:B。
【点评】此题重点考查从折线统计图中读取信息进行分析。
二.填空题(共9小题)
10.【答案】(1)120,150;(2)路程,时间,时间;(3)速度,成。
【分析】根据路程÷时间=速度=30(一定),所以路程和时间是两个相关联的量,路程是随着时间的变化而变化的。这两个量中相对应的两个数的比值一定,这两个量就叫做成正比例的量,它们的关系叫做正比例的关系。
【解答】解:(1)4×30﹣120(km)
5×30=150(km)
时间/时 1 2 3 4 5
路程/km 30 60 90 120 150
(2)路程和时间是两种相关联的量,路程随着时间的变化而变化。
(3)从表中可以看出,轮船行驶的速度一定,轮船行驶的路程和时间成正比例。
故答案为:120,150;路程,时间,时间;速度,成。
【点评】此题主要考查对正比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的相对应的比值一定,这两种量成正比例。
11.【答案】(1)正;正;(2)1:2。
【分析】(1)由图象可以得到零件的个数与天数的比例关系;
(2)由天数为1天时对应的个数为5和10,即可解答题目。
【解答】解:(1)由图象可以判断,加工A型零件的个数和天数成正比例,加工B型零件的个数和天数成正比例。
(2)5:10=1:2
答:每个工人生产A型零件和B型零件的工作效率比是1:2。
故答案为:正;正;1:2。
【点评】本题考查正比例的认识,熟练掌握正比例的意义是解题的关键。
12.【答案】(1)正。
(2)16,4。
(3)96。
【分析】(1)图像是一条直线,所以总价和支数成正比例关系。
(2)从图像中可以看出,每支笔的单价为8元,根据总价=单价×数量、数量=总价÷单价解答。
(3)根据总价=单价×数量解答。
【解答】解:(1)图中总价是随着支数的变化而变化,这两种量成正比例。
(2)8×2=16(元)
32÷8=4(支)
答:售出2支笔的总价是16元,售出4支笔的总价是32元。
(3)8×12=96(元)
答:售出了12支笔,总价是96元。
故答案为:正;16,4;96。
【点评】本题考查了根据比例图像解决问题,能根据图像分析数量关系是关键。
13.【答案】见试题解答内容
【分析】根据路程、时间和速度的关系,求出路程和时间的比的比值即速度,如果速度一定,也就是比值一定,路程和时间就成正比例.
【解答】解:路程:时间=速度(一定),也就是比值一定,路程和时间就成正比例.
故答案为:速度,正.
【点评】解决关键是先求出路程和时间的比的比值,再根据比值一定,判断路程和时间成正比例.
14.【答案】②。
【分析】从三幅图中找出几组对应的x与y,并求出它们的商;根据如果商一定就成正比例,据此计算即可解答题目。
【解答】解:A:4÷2=2,16÷4=4,则两种量的比值是不一定的,所以不成正比例的关系;
B:4÷1=4,8÷2=4,则图中的两种量的比值是一定的,都是4,所以成正比例的关系;
C:2÷6,4÷4=1,则两种量的比值是不一定的,所以不成正比例的关系。
故答案为:②。
【点评】本题是一道关于正比例方面的题目,可依据判断正比例的方法以及正比例的意义求解。
15.【答案】200;4;正。
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【解答】解:
时间/小时 2 4
路程/千米 200 400
这辆汽车行驶的路程和时间成正比例。
故答案为:200;4;正。
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断。
16.【答案】(1)船费,人数,人数;(2)5,每人所付的船费;(3)所付船费,船费,人数,正。
【分析】(1)上表中,表格中的船费和人数是两种相关联的量,船费随着人数的变化而变化;
(2)求船费与人数数量中相对应的两个数的比值,用船费:人数=每人所付的船费,所以这个比值表示每人所付的船费;
(3)因为船费:人数=每人所付的船费,每人所付船费一定,所以船费和人数成正比例关系;据此解答。
【解答】解:(1)表格中的船费和人数是两种相关联的量,船费随着人数的变化而变化;
(2)5:1=10:2
答:船费与人数数量中相对应的两个数的比值是5,这个比值实际上表示每人所付的船费;
(3)因为每人的所付船费一定,所以船费和人数成正比例关系。
故答案为:船费,人数,人数;5,每人所付的船费;所付船费,船费,人数,正。
【点评】此题主要考查正比例的意义以及总价、数量和单价之间的关系,正比例的意义是:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量。
17.【答案】(1)1,80,5,200;(2)在;(3)80。
【分析】(1)图中直观显示,点A表示汽车1时行驶了80km;行驶400km需要5时;2.5时行驶了200km。
(2)从图上可知汽车1时行驶了80km,点中10表示10时,求出汽车10时行驶的路程,与800比较即可。
(3)根据速度=路程÷时间可求得。
【解答】解:(1)80×2.5=200(km)
点A表示汽车1时行驶了80km;行驶400km需要5时;2.5时行驶了200km。
(2)80×10=800(km)
答:点(10,800)在这条直线上。
(3)160÷2=80(千米/时)
答:这辆汽车的速度是80千米/时。
故答案为:1,80,5,200;在;80。
【点评】此题考查了正比例关系的图象的应用,利用数形结合的思想解决问题是常用的一种数学思想方法。
18.【答案】20,12.8
【分析】(1)如果x与y成正比例,由正比例的意义可得4:16=5:m,把m看作未知数,根据比例的基本性质进行解比例即可;
(2)如果x和y成反比例,由反比例的意义可得5×m=4×16,把m看作未知数,根据等式的性质进行解方程即可。
【解答】解:根据题意可得:
(1)4:16=5:m
4m=16×5
4m=80
4m÷4=80÷4
m=20
所以,如果x与y成正比例,“m”是20;
(2)5×m=4×16
5m=64
5m÷5=64÷5
m=12.8
所以,如果x和y成反比例,“m”是12.8。
故答案为:20,12.8
【点评】本题主要考查正反比例的意义,然后根据题意列出比例或方程再进一步解答即可.
三.判断题(共10小题)
19.【答案】见试题解答内容
【分析】要想判定x和y成不成正比例关系,必须根据式子,进行推导.再根据正比例的意义,分析数量关系,找出一定的量,看看x和y是不是比值一定.
【解答】解:因为 yx(x≠0),
所以 y:x(一定),
可以看出,y和x是两个相关联的变化的量,它们相对应的数的比值是,是一定的,所以y和x成正比例关系.
故答案为:√.
【点评】此题重点考查正比例的意义.
20.【答案】√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:长方体的体积=底面积×高,高=长方体的体积÷底面积。长方体的高一定,所以它的体积和底面积成正比例关系,原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
21.【答案】×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:如果一个量变大,另一个量也变大,但比值不一定,所以这两量不成正比例,所以原题说法错误。
故答案为:×。
【点评】此题考查了判断两个相关联的量之间成什么比例的方法。
22.【答案】见试题解答内容
【分析】订阅《少年文艺》的份数与总钱数是两种相关联的量,总钱数÷份数=每份的钱数,每份的钱数,即单价一定,也就是这两种量的比值一定,所以成正比例,不成反比例.
【解答】解:总钱数÷份数=每份的钱数,
每份的钱数,即单价一定,也就是这两种量的比值一定,所以成正比例;
故答案为:×.
【点评】此题考查辨识成正比例的量,只要两种相关联的量比值一定,就成正比例.
23.【答案】√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:因为花生的总质量:袋数=每袋的质量(一定),是比值一定,所以花生的总质量和袋数成正比例,所以原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
24.【答案】×
【分析】成正比例的两个量的比值一定,所以是一条直线。
【解答】解:成正比例的两个量的比值一定,所以是一条直线。
故答案为;×。
【点评】本题考查了学生对成正比例的两个量的关系的理解。
25.【答案】×
【分析】两种相关联的量中相对应的两个数的商一定,就成正比例关系,正比例的图象是一条过原点的直线。
【解答】解:两种相关联的量中相对应的两个数的商一定,就成正比例关系,正比例的图象是一条过原点的直线。所以原题干错误。
故答案为:×。
【点评】本题考查的是正比例的意义,熟知正比例函数的图象是经过原点的一条直线是解答此题的关键。
26.【答案】见试题解答内容
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例.
【解答】解:正方体的表面积÷一个面的面积=6(一定),是比值一定,所以正方体的一个面的面积和它的表面积成正比例;
故答案为:正.
【点评】此题属于根据正、反比例的意义,判断两种相关联的量是成正比例还是成反比例,就看两种量是对应的比值一定,还是对应的乘积一定,再做出解答.
27.【答案】×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此分析。
【解答】解:如果ab÷5=17,ab=17×5=85(一定),是两个量的乘积一定,则a与b成反比例;原题说法错误。
故答案为:×。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
28.【答案】见试题解答内容
【分析】判断本数和总价是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果是比值不一定,就不成正比例.
【解答】解:总价÷本数=每本书的单价(一定),是比值一定,本数和总价就成正比例.
故判断为:正确.
【点评】此题属于辨识成正比例的量,就看这两种量是否是对应的比值一定,再做出判断.
四.应用题(共1小题)
29.【答案】40块。
【分析】根据题意知道,地砖的面积一定,房子的面积÷地砖的块数=地砖的面积(一定),所以房子的面积与方砖的块数成正比例,由此列出比例解答即可。
【解答】解:设用同样的地砖,需要X块。
16:32=20:X
16X=640
X=40
答:用同样的地砖,需要40块。
【点评】关键是判断出房子的面积与方砖的块数成正比例,由此解决问题。
