探索三角形全等的条件

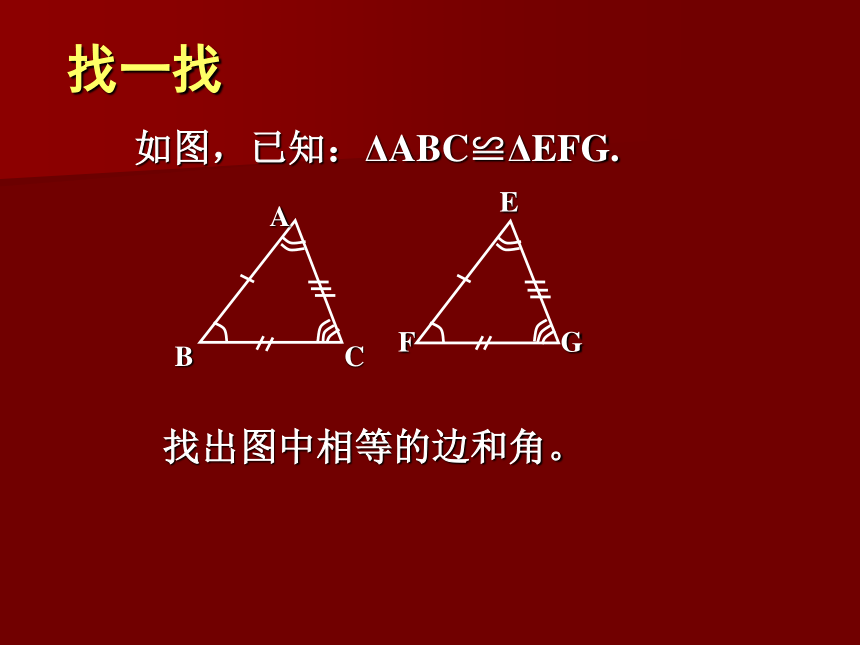
课件19张PPT。课前准备昨日重现1.什么叫做全等三角形？ 两个能够重合的三角形叫做全等三角形。2.全等三角形有怎样的性质？全等三角形的对应边相等,对应角相等。找一找如图，已知：ΔABC≌ΔEFG. EFG 找出图中相等的边和角。第五章第五节探索三角形全等的条件（一） 两个能够重合的三角形是全等三角形。重合实质上是六个元素的对应相等（三条边对应相等、三个角对应相等），
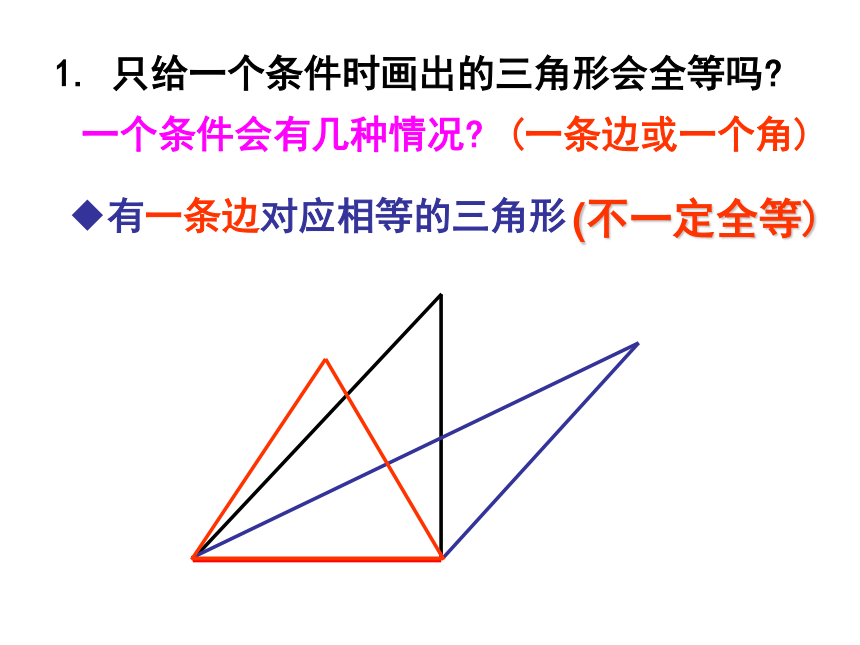
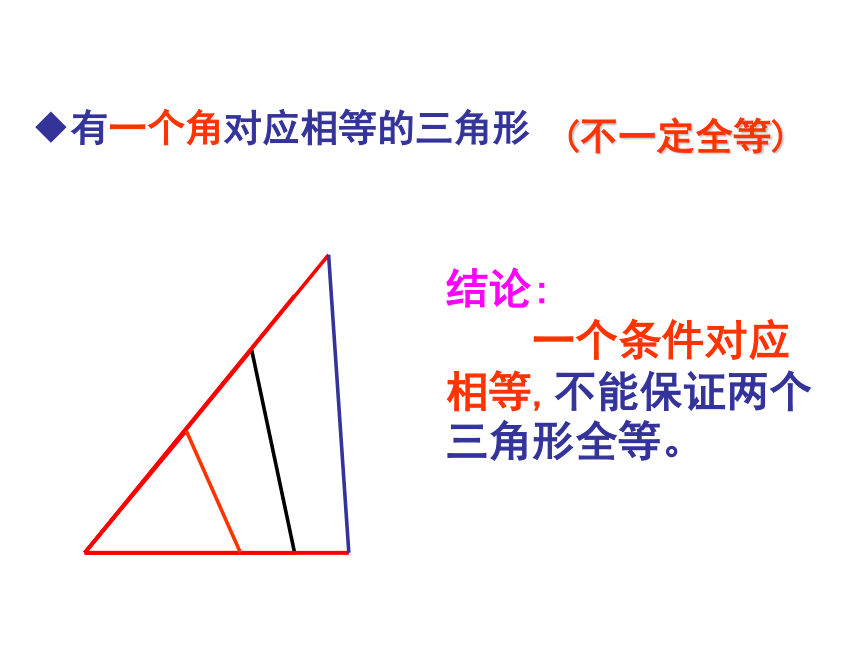
用六个元素的对应相等来判断两个三角形的全等实在显得麻烦。因此，我们必须找到一些简单的方法，即用最少元素的对应相等来判断两个三角形的全等。这就需要我们认真细致地来探索。就让我们从最简单的来开始吧! 1. 只给一个条件时画出的三角形会全等吗?有一条边对应相等的三角形(不一定全等) (一条边或一个角) 一个条件会有几种情况?有一个角对应相等的三角形结论:
一个条件对应相等,不能保证两个三角形全等。
(不一定全等)(不一定全等) 一个角为30°,一条边为6cm的三角形 2. 给出两个条件呢?30o 6cm 两个条件有几种情况呢? (一角一边、两条边 或两个角) （1）一角一边：(2)两条边：
两条边分别是4cm和6cm的三角形(不一定全等)(3)两个角
两个角分别是30°和60°的三角形结论：
有两个条件对应相等，也不能保证两个三角形全等.(不一定全等)3. 给三个条件呢?(1)三个角;
(2)三条边;
(3)两角一边;
(4)两边一角. 三个条件会有几种情况呢?（1）三个角：
三个角分别为30°、60°和90°的三角形 结论:
三个内角对应相等的三角形不一定全等。(不一定全等)（2）三条边
三条边分别为4cm，5cm，7cm的三角形(一定全等)结论:
三条边对应相等的两个三角形一定全等。三角形全等的条件: 1. 三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” S ——边AB=A’B’BC=B’C’AC=A’C’（SSS）符号表达式：在△ABC和△A'B'C'中所以两角一边 有几种可能的情况呢？（3）两角一边 1）边是两角所加夹的边，
2）边是其中一角的对边。 1） 两个内角分别是60°和80°，它们所夹的边为3cm的三角形 3cm结论：两角和它们的夹边对应相等的两个三角形全等。三角形全等的条件:A ——角2. 两角和它们的夹边对应相等的两个三角形全等。简写成“角边角”或“ASA” 2） 两个内角分别是60°和40°，其中40°角所对的边为3cm的三角形 (一定全等)三角形全等的条件: 3. 两角和其中一角的对边对应相等的两个三角形全等，简写成“角角边”或“AAS”。三角形全等的条件: 1. 三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” 2. 两角和它们的夹边对应相等的两个
三角形全等。简写成“角边角”或“ASA”。3.两角和其中一角的对边对应相等的两个三
角形全等。简写成“角角边”或“AAS”。本节概要