2015年沪科版数学九年级上册单元梯度检测精品卷:(七)第23章解直角三角形单元梯度检测A卷
文档属性
| 名称 | 2015年沪科版数学九年级上册单元梯度检测精品卷:(七)第23章解直角三角形单元梯度检测A卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 387.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-10 00:00:00 | ||
图片预览


文档简介
(七)第23章解直角三角形单元梯度检测A卷
(满分:150分 时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.如图,在平面直角坐标系的第一象限内有一点A,它的坐标为(x,y),直线AO与x轴正半轴的夹角为,则的正弦值为……………………………………………【 】
A. B. C. D.
2.在Rt△ABC中,若将各边的长都扩大为原来的n倍,则锐角A的余弦值将………【 】
A. 扩大为原来的n倍 B. 缩小为原来的n倍
C.没有变化 D.不能确定
3.在Rt△ABC中,∠C=90°,则下列关系式:①0<sinA<1;②sinA+sinB>1;③sin2A+sin2B=1;④sinA=sinB·tanA.其中正确的有……………………………………【 】
A.①②③④ B.①② C. D.6
4.如图,在△ABC中,AC=BC=10,sin∠CAB=0.6,则AC边上的高为……………【 】
A.9.8 B.9.6 C.8 D.6
5.在△ABC中,AC=5,AB=13,则tanA的值为……………………………………【 】
A. B. C. D.不确定
6. 在△ABC中,AB=12,BC=8,AD是BC边上的高,AD=6,则tanC的值为【 】
A. B.或 C. D.2或
7.如图,某人沿一斜坡前进10m,此时他上升了6m,则此斜坡的坡度i=……………【 】
A.1︰ B. 1︰0.75 C. D. 0.8
8.如图,我校准备从地面A点向国旗杆底座上部B点修建阶梯AB,已知AC=1.5m,每阶的高不超过15cm,则此阶梯至少要建(≈1.732,最后一阶的高不足15cm时按一阶计)…………………………………………………………………………………【 】
A.4阶 B.5阶 C.6阶 D.7阶
9.如图,我市和平小学准备在一块如图所示的三角形空地上种植花草以美化校园,若请园林工人种植花草需2元/m2,,学校发动师生自己动手种植花草需1.5元/m2,则学校发动师生自己动手种植花草可节约资金…………………………………………【 】
A.468.75元 B.312.5元 C.156.25元 D.625元
10.如图,某水渠的横断面为四边形ABCD,AB∥CD,∠DAB=∠CBA=120°,设AD=x,四边形ABCD的周长为 y,在水流速度一定的情况下,水流量与水渠横断面面积成正比,要使水渠的流量最大,则x与y应满足的关系是……………………………【 】
A.y=3x B. y=4x C. y=5x D. y=6x
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知在△ABC中,∠C=90°,两直角边分别为a、b,且a、b满足方程a2-4ab+3b2=0,则sinB=___________.
12.如图,在□ABCD中,DE⊥AC于点E,∠BDE=30°,DE=1,则DB=_____________.
13.如图,在等腰Rt△ABC中,∠C=90°,AC=5,D为AC上一点,若tan∠DBA=,则tan∠DBC= _______________.
14.如图,为了测量我市电视塔MN的高度,在塔前的平地上选择一点P,测得看塔顶的仰角为30°,从P点向塔底N走100m到达Q点,测得看塔顶的仰角为45°,则电视塔MN的高度为____________m.
三、(本大题共两小题,每小题8分,满分16分)
15.计算:﹣2﹣2+tan30°-sin245°+.
16.如图,在矩形ABCD中,DE⊥AC于点E,∠CDE=∠,DA=8,DC=15,试求∠的三个三角函数值.2·1·c·n·j·y
四、(本大题共两小题,每小题8分,满分16分)
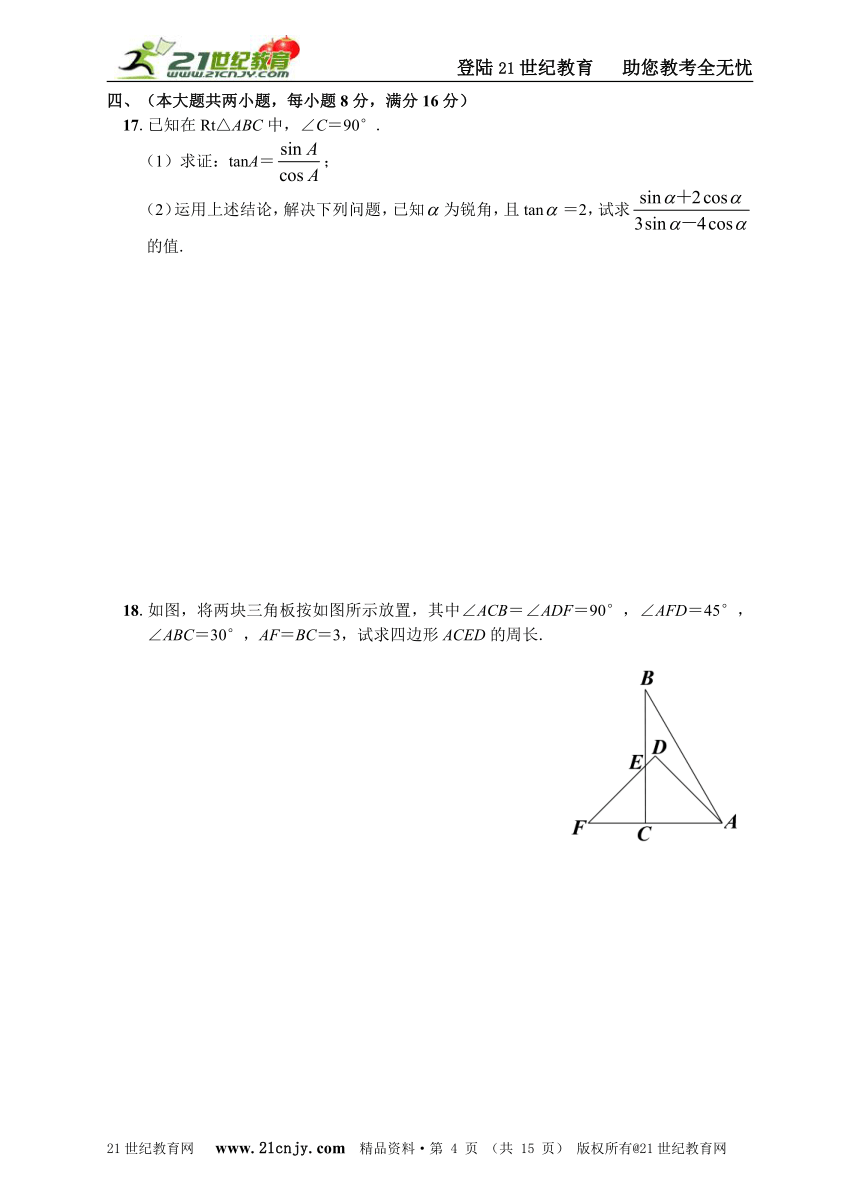
17.已知在Rt△ABC中,∠C=90°.
(1)求证:tanA=;
(2)运用上述结论,解决下列问题,已知为锐角,且tan=2,试求的值.
18.如图,将两块三角板按如图所示放置,其中∠ACB=∠ADF=90°,∠AFD=45°,∠ABC=30°,AF=BC=3,试求四边形ACED的周长.
五、(本大题共两小题,每小题10分,满分20分)
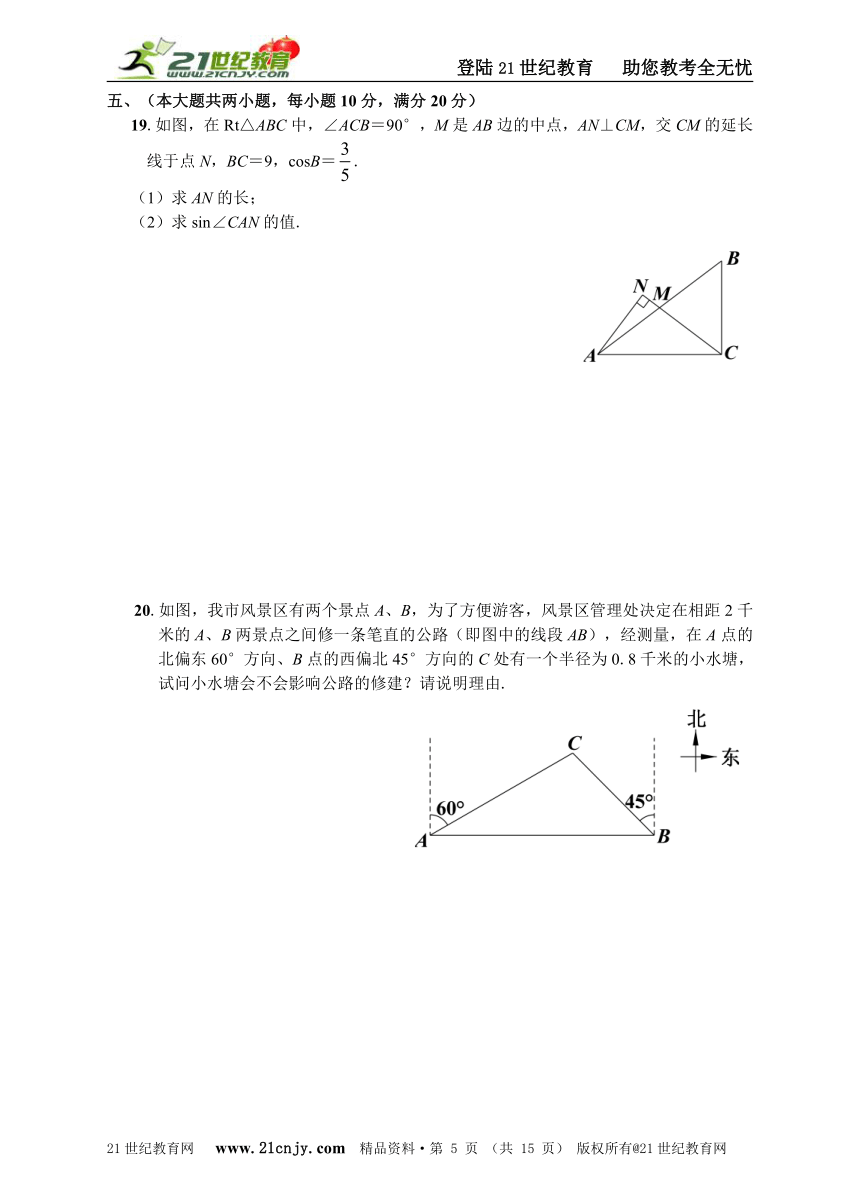
19.如图,在Rt△ABC中,∠ACB=90°,M是AB边的中点,AN⊥CM,交CM的延长线于点N,BC=9,cosB=.【来源:21·世纪·教育·网】
(1)求AN的长;
(2)求sin∠CAN的值.
20.如图,我市风景区有两个景点A、B,为了方便游客,风景区管理处决定在相距2千米的A、B两景点之间修一条笔直的公路(即图中的线段AB),经测量,在A点的北偏东60°方向、B点的西偏北45°方向的C处有一个半径为0.8千米的小水塘,试问小水塘会不会影响公路的修建?请说明理由.【来源:21cnj*y.co*m】
六、(本题满分12分)
21.如图,为了测量我校教学楼前的一座景观石的高度,在教学楼二楼的C点处测得顶部A点的仰角为30°,底部B点的俯角为45°,又在五楼的D点测得顶部A点的俯角为60°,已知CD=10m,试求景观石AB的高度(≈1.7,结果保留整数).
七、(本题满分12分)
22.如图,我市防汛指挥部发现在我市的长江段有一处长300m,高6m,背水坡的坡角为45°的防洪大堤急需加固,其横截面为梯形ABCD,防汛专家制定方案:背水坡面用土石进行加固,使上底加宽1m,加固后背水坡EF的坡比i=1︰2.
(1)求加固后坝底增加的宽度BE的长;
(2)求完成这项工程需要土石多少立方米?
八、(本题满分14分)
23.如图,池塘中央有一棵大树,在数学活动课上余老师带领同学们去测量这棵大树的
高度,现有测角仪和皮尺两种测量工具,请你设计一种测量方案,测出这棵树的高
度AB,要求:
(1)请你画出测量示意图并写出测量步骤(测量所得数据均用字母表示);
(2)根据(1)中的数据计算这棵树的高度AB.
参考答案
1.D 解析:如下图,过点A作AB⊥x轴于点B,则OB==x,AB==y,在Rt△OAB中,由勾股定理得OA=,∴sin===,∴D对. 21世纪教育网版权所有
2.C 解析:锐角三角函数值的大小只与角的度数有关,与其他因素无关,∴C对.
3.A 解析:∵a<c,∴0<<1,∵sinA=,∴0<sinA<1,∴①正确;∵sinA=,sinB=,∴sinA+sinB=+=,∵a+b>c,∴>1,∴sinA+sinB>1,∴②正确;∵sinA=,sinB=,∴sin2A+sin2B=+=,∵a2+b2=c2,∴=1,∴sin2A+sin2B=1,∴③正确;∵sinA=,sinB=,tanA=,∴sinB·tanA=×==sinA,∴④正确.∴A对.
4.B 解析:如下图,过点C作CD⊥AB于点D,过点B作BE⊥AC,交AC的延长线于点E,∵AC=BC,∴AD=BD,在Rt△CAD中,sin∠CAD==0.6,∴CD=0.6×CA=0.6×10=6,由勾股定理得AD===8,∴AB=16,∵S△ABC=×AB×CD=×AC×BE,∴BE===9.6,,∴B 对. 21教育网
5.D 解析:∵△ABC不一定是直角三角形,∴tanA的值不能确定,∴D对.
6.B 解析:当AD在△ABC内部时,如下图①,在Rt△ABD中,由勾股定理得BD===6,∴CD=BC-BD=8-6=2,在Rt△ADC中,tanC===;当AD在△ABC外部时,如下图②,在Rt△ABD中,由勾股定理得BD===6,∴CD=BC+BD=8+6=14,在Rt△ADC中,tanC===.∴综上,tanC的值为或.∴B对. 21cnjy.com
7.A 解析:如下图,斜坡AB=10,过点B作BC⊥AC于点C,此时斜坡高度BC=6,在Rt△ABC中,由勾股定理得AC===8,∴斜坡坡度i====1︰∴A对. 21·cn·jy·com
8.C 解析:在Rt△ABC中,∠A=30°,AC=1.5,∵tanA=,∴BC=AC·tanA=1.5×=,÷0.15≈6(阶),∴C对. www.21-cn-jy.com
9.C 解析:如下图,过点A作AD⊥BC,交BC的延长线于点D,∵∠ACB=135°,∴∠ACD=45°,又AC=25,∴在Rt△ACD中由sin∠ACD=得AD=AC×sin45°=25×=25,∴S△ABC=×BC×AD=×25×25=312.5,∴可节约的资金为312.5×(2-1.5)=156.25(元),∴C对.
10.B 解析:如下图,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,由题意得Rt△AED≌△BFC,四边形ABFE为矩形,∵∠DAB=∠CBA=120°,∴∠D=∠C=60°,∵AD=BC=x,∴DE=CF=x,由勾股定理得AE=BF==x,设水渠流量为z,则z=(y-2x)×x=﹣x2+xy=﹣(x-y)2+y2,当x=y时,z最大,∴当y=4x时,水渠的流量最大,∴B对. 21·世纪*教育网
11. 或 解析:解方程a2-4ab+3b2=0,得a=b或a=3b,当a=b时,c=b,∴sinB==;当a=3b时,c=b,∴sinB==.∴sinB=或. 21*cnjy*com
12. 解析:在Rt△ODE中,cos∠ODE=,∵∠BDE=30°,DE=1,∴OD===,∵四边形ABCD为平行四边形,∴DB=2DO=.
13. 解析:如下图,过点D作DE⊥AB于点E,在Rt△ABC中,AC=BC=5,由勾股定理得AB=5,在等腰Rt△ADE中,设AD=DE=x,则由勾股定理得AD=x,在Rt△DEB中,tan∠DBE==,∴BE=4x,∴AB=BE+AE=5x=5,∴x=,∴AD=2,∴CD=3,∴在Rt△DBC中,tan∠DBC==.【出处:21教育名师】
14. (50+50) 解析:在Rt△MNQ中,设MN=x,∵∠MQN=45°,tan∠MQN=,∴QN==x,在Rt△MNP中,MN=x,∵∠MPN=30°,tan∠MPN=,∴PN==x,∵PN-QN=PQ,∴x-x=100,解得x=50+50=MN.【版权所有:21教育】
15.解:原式=﹣+2×-()2+=﹣+2-+=2.
16.解:∵四边形ABCD是矩形,∴∠CDA=90°,在Rt△ADC中,DA=8,DC=15,∴由勾股定理得AC===17,∵DE⊥AC,∴∠=∠CDA,∴sin∠=sin∠CDA==,cos∠=cos∠CDA==,tan∠=tan∠CDA==.21教育名师原创作品
17.解:(1)∵sinA=,cosA=,∴==×=,∵tanA=,∴tanA=;21*cnjy*com
(2)由(1)得tan=,又tan=2,∴=2,∴sin=2 cos,代入得==2.
18.解:在Rt△ABC中,∠B=30°,BC=3,tan∠B=,∴AC=BC×tan30°=3× =,∴FC=AF-AC=3-,在等腰Rt△ADF中,∠F=45°,AF=3,sin∠F=,∴AD=AF×sin45°=3×==DF,又在等腰Rt△FCE中,∠F=45°,FC=EC=3-,cos∠F=,∴FE===3-,∴DE=DF-EF=-3+=-,∴AC+EC+DE+AD=+3-+-+=3+,即四边形ACED的周长为3+.
(2)在Rt△AMN中,由勾股定理得MN===2.1,∴
CN=CM+MN=7.5+2.1=9.6,∴在Rt△ACN中,sin∠CAN===.
20.解:小水塘会影响公路的修建,理由如下:如下图,过点C作CD⊥AB于点D,设CD=x,在Rt△CDB中,∠CDB=90°,∠CBD=45°,tan∠CBD=,∴BD==x,在Rt△CDA中,∠CDA=90°,∠CAD=30°,tan∠CAD=,∴AD==x,又AB=AD+BD=2,∴x+x=2,解得x=-1,∵-1≈0.732<0.8,小水塘会影响公路的修建.
21.解:如下图,过点C作CF⊥AB于点F,∵∠ADC=90°-60°=30°,∠ACD=90°-30°=60°,∴∠CAD=90°,∵CD=10,∴AC=CD=5,在Rt△ACF中,AF=ACsin30°=5×=,CF=ACcos30°=5×=,在Rt△BCF中,∵∠BCF=45°,BF=ACtan30°=5×=,∴AB=AF+BF=+≈9(m).答:景观石AB的高度约为9m.
22.解:(1)如下图,过点A作AQ⊥BC于点Q,过点F作FP⊥BC于点P,则AF=PQ=1,AQ=FP=6,在Rt△ABQ中,∠ABQ=45°,tan∠ABQ=,∴BQ==6,∴BP=BQ-PQ=6-1=5,在Rt△EFP中,i=1︰2=,∴EP=2FP=12,∴EB=EP-BP=12-5=7;www-2-1-cnjy-com
(2)S梯形AFEB=(FA+EB)×FP=(1+7)×6=24,24×300=7200(m3)∴完成这项工程需要土石7200立方米.
23.解:(1)测量示意图如下图;测量步骤:①用皮尺测出测角仪的高度h;②在地面上选择点C安装测角仪并测出此时树顶A点的仰角∠ADE=;③沿CB前进到点F,用皮尺测出点C、F之间的距离CF=l;④在点F处安装测角仪,测得此时树顶A点的仰角∠AGE=.2-1-c-n-j-y
(2)观察测量示意图,设AE=x,在Rt△ADE中,tan∠ADE=,∴DE=-,在Rt△AGE中,tan∠AGE=,∴GE=,∵DE-GE=DG=CF=l,∴=l,解得x=,∴AB=AE+EB=AE+CD=+h.
(满分:150分 时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.如图,在平面直角坐标系的第一象限内有一点A,它的坐标为(x,y),直线AO与x轴正半轴的夹角为,则的正弦值为……………………………………………【 】
A. B. C. D.
2.在Rt△ABC中,若将各边的长都扩大为原来的n倍,则锐角A的余弦值将………【 】
A. 扩大为原来的n倍 B. 缩小为原来的n倍
C.没有变化 D.不能确定
3.在Rt△ABC中,∠C=90°,则下列关系式:①0<sinA<1;②sinA+sinB>1;③sin2A+sin2B=1;④sinA=sinB·tanA.其中正确的有……………………………………【 】
A.①②③④ B.①② C. D.6
4.如图,在△ABC中,AC=BC=10,sin∠CAB=0.6,则AC边上的高为……………【 】
A.9.8 B.9.6 C.8 D.6
5.在△ABC中,AC=5,AB=13,则tanA的值为……………………………………【 】
A. B. C. D.不确定
6. 在△ABC中,AB=12,BC=8,AD是BC边上的高,AD=6,则tanC的值为【 】
A. B.或 C. D.2或
7.如图,某人沿一斜坡前进10m,此时他上升了6m,则此斜坡的坡度i=……………【 】
A.1︰ B. 1︰0.75 C. D. 0.8
8.如图,我校准备从地面A点向国旗杆底座上部B点修建阶梯AB,已知AC=1.5m,每阶的高不超过15cm,则此阶梯至少要建(≈1.732,最后一阶的高不足15cm时按一阶计)…………………………………………………………………………………【 】
A.4阶 B.5阶 C.6阶 D.7阶
9.如图,我市和平小学准备在一块如图所示的三角形空地上种植花草以美化校园,若请园林工人种植花草需2元/m2,,学校发动师生自己动手种植花草需1.5元/m2,则学校发动师生自己动手种植花草可节约资金…………………………………………【 】
A.468.75元 B.312.5元 C.156.25元 D.625元
10.如图,某水渠的横断面为四边形ABCD,AB∥CD,∠DAB=∠CBA=120°,设AD=x,四边形ABCD的周长为 y,在水流速度一定的情况下,水流量与水渠横断面面积成正比,要使水渠的流量最大,则x与y应满足的关系是……………………………【 】
A.y=3x B. y=4x C. y=5x D. y=6x
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知在△ABC中,∠C=90°,两直角边分别为a、b,且a、b满足方程a2-4ab+3b2=0,则sinB=___________.
12.如图,在□ABCD中,DE⊥AC于点E,∠BDE=30°,DE=1,则DB=_____________.
13.如图,在等腰Rt△ABC中,∠C=90°,AC=5,D为AC上一点,若tan∠DBA=,则tan∠DBC= _______________.
14.如图,为了测量我市电视塔MN的高度,在塔前的平地上选择一点P,测得看塔顶的仰角为30°,从P点向塔底N走100m到达Q点,测得看塔顶的仰角为45°,则电视塔MN的高度为____________m.
三、(本大题共两小题,每小题8分,满分16分)
15.计算:﹣2﹣2+tan30°-sin245°+.
16.如图,在矩形ABCD中,DE⊥AC于点E,∠CDE=∠,DA=8,DC=15,试求∠的三个三角函数值.2·1·c·n·j·y
四、(本大题共两小题,每小题8分,满分16分)
17.已知在Rt△ABC中,∠C=90°.
(1)求证:tanA=;
(2)运用上述结论,解决下列问题,已知为锐角,且tan=2,试求的值.
18.如图,将两块三角板按如图所示放置,其中∠ACB=∠ADF=90°,∠AFD=45°,∠ABC=30°,AF=BC=3,试求四边形ACED的周长.
五、(本大题共两小题,每小题10分,满分20分)
19.如图,在Rt△ABC中,∠ACB=90°,M是AB边的中点,AN⊥CM,交CM的延长线于点N,BC=9,cosB=.【来源:21·世纪·教育·网】
(1)求AN的长;
(2)求sin∠CAN的值.
20.如图,我市风景区有两个景点A、B,为了方便游客,风景区管理处决定在相距2千米的A、B两景点之间修一条笔直的公路(即图中的线段AB),经测量,在A点的北偏东60°方向、B点的西偏北45°方向的C处有一个半径为0.8千米的小水塘,试问小水塘会不会影响公路的修建?请说明理由.【来源:21cnj*y.co*m】
六、(本题满分12分)
21.如图,为了测量我校教学楼前的一座景观石的高度,在教学楼二楼的C点处测得顶部A点的仰角为30°,底部B点的俯角为45°,又在五楼的D点测得顶部A点的俯角为60°,已知CD=10m,试求景观石AB的高度(≈1.7,结果保留整数).
七、(本题满分12分)
22.如图,我市防汛指挥部发现在我市的长江段有一处长300m,高6m,背水坡的坡角为45°的防洪大堤急需加固,其横截面为梯形ABCD,防汛专家制定方案:背水坡面用土石进行加固,使上底加宽1m,加固后背水坡EF的坡比i=1︰2.
(1)求加固后坝底增加的宽度BE的长;
(2)求完成这项工程需要土石多少立方米?
八、(本题满分14分)
23.如图,池塘中央有一棵大树,在数学活动课上余老师带领同学们去测量这棵大树的
高度,现有测角仪和皮尺两种测量工具,请你设计一种测量方案,测出这棵树的高
度AB,要求:
(1)请你画出测量示意图并写出测量步骤(测量所得数据均用字母表示);
(2)根据(1)中的数据计算这棵树的高度AB.
参考答案
1.D 解析:如下图,过点A作AB⊥x轴于点B,则OB==x,AB==y,在Rt△OAB中,由勾股定理得OA=,∴sin===,∴D对. 21世纪教育网版权所有
2.C 解析:锐角三角函数值的大小只与角的度数有关,与其他因素无关,∴C对.
3.A 解析:∵a<c,∴0<<1,∵sinA=,∴0<sinA<1,∴①正确;∵sinA=,sinB=,∴sinA+sinB=+=,∵a+b>c,∴>1,∴sinA+sinB>1,∴②正确;∵sinA=,sinB=,∴sin2A+sin2B=+=,∵a2+b2=c2,∴=1,∴sin2A+sin2B=1,∴③正确;∵sinA=,sinB=,tanA=,∴sinB·tanA=×==sinA,∴④正确.∴A对.
4.B 解析:如下图,过点C作CD⊥AB于点D,过点B作BE⊥AC,交AC的延长线于点E,∵AC=BC,∴AD=BD,在Rt△CAD中,sin∠CAD==0.6,∴CD=0.6×CA=0.6×10=6,由勾股定理得AD===8,∴AB=16,∵S△ABC=×AB×CD=×AC×BE,∴BE===9.6,,∴B 对. 21教育网
5.D 解析:∵△ABC不一定是直角三角形,∴tanA的值不能确定,∴D对.
6.B 解析:当AD在△ABC内部时,如下图①,在Rt△ABD中,由勾股定理得BD===6,∴CD=BC-BD=8-6=2,在Rt△ADC中,tanC===;当AD在△ABC外部时,如下图②,在Rt△ABD中,由勾股定理得BD===6,∴CD=BC+BD=8+6=14,在Rt△ADC中,tanC===.∴综上,tanC的值为或.∴B对. 21cnjy.com
7.A 解析:如下图,斜坡AB=10,过点B作BC⊥AC于点C,此时斜坡高度BC=6,在Rt△ABC中,由勾股定理得AC===8,∴斜坡坡度i====1︰∴A对. 21·cn·jy·com
8.C 解析:在Rt△ABC中,∠A=30°,AC=1.5,∵tanA=,∴BC=AC·tanA=1.5×=,÷0.15≈6(阶),∴C对. www.21-cn-jy.com
9.C 解析:如下图,过点A作AD⊥BC,交BC的延长线于点D,∵∠ACB=135°,∴∠ACD=45°,又AC=25,∴在Rt△ACD中由sin∠ACD=得AD=AC×sin45°=25×=25,∴S△ABC=×BC×AD=×25×25=312.5,∴可节约的资金为312.5×(2-1.5)=156.25(元),∴C对.
10.B 解析:如下图,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,由题意得Rt△AED≌△BFC,四边形ABFE为矩形,∵∠DAB=∠CBA=120°,∴∠D=∠C=60°,∵AD=BC=x,∴DE=CF=x,由勾股定理得AE=BF==x,设水渠流量为z,则z=(y-2x)×x=﹣x2+xy=﹣(x-y)2+y2,当x=y时,z最大,∴当y=4x时,水渠的流量最大,∴B对. 21·世纪*教育网
11. 或 解析:解方程a2-4ab+3b2=0,得a=b或a=3b,当a=b时,c=b,∴sinB==;当a=3b时,c=b,∴sinB==.∴sinB=或. 21*cnjy*com
12. 解析:在Rt△ODE中,cos∠ODE=,∵∠BDE=30°,DE=1,∴OD===,∵四边形ABCD为平行四边形,∴DB=2DO=.
13. 解析:如下图,过点D作DE⊥AB于点E,在Rt△ABC中,AC=BC=5,由勾股定理得AB=5,在等腰Rt△ADE中,设AD=DE=x,则由勾股定理得AD=x,在Rt△DEB中,tan∠DBE==,∴BE=4x,∴AB=BE+AE=5x=5,∴x=,∴AD=2,∴CD=3,∴在Rt△DBC中,tan∠DBC==.【出处:21教育名师】
14. (50+50) 解析:在Rt△MNQ中,设MN=x,∵∠MQN=45°,tan∠MQN=,∴QN==x,在Rt△MNP中,MN=x,∵∠MPN=30°,tan∠MPN=,∴PN==x,∵PN-QN=PQ,∴x-x=100,解得x=50+50=MN.【版权所有:21教育】
15.解:原式=﹣+2×-()2+=﹣+2-+=2.
16.解:∵四边形ABCD是矩形,∴∠CDA=90°,在Rt△ADC中,DA=8,DC=15,∴由勾股定理得AC===17,∵DE⊥AC,∴∠=∠CDA,∴sin∠=sin∠CDA==,cos∠=cos∠CDA==,tan∠=tan∠CDA==.21教育名师原创作品
17.解:(1)∵sinA=,cosA=,∴==×=,∵tanA=,∴tanA=;21*cnjy*com
(2)由(1)得tan=,又tan=2,∴=2,∴sin=2 cos,代入得==2.
18.解:在Rt△ABC中,∠B=30°,BC=3,tan∠B=,∴AC=BC×tan30°=3× =,∴FC=AF-AC=3-,在等腰Rt△ADF中,∠F=45°,AF=3,sin∠F=,∴AD=AF×sin45°=3×==DF,又在等腰Rt△FCE中,∠F=45°,FC=EC=3-,cos∠F=,∴FE===3-,∴DE=DF-EF=-3+=-,∴AC+EC+DE+AD=+3-+-+=3+,即四边形ACED的周长为3+.
(2)在Rt△AMN中,由勾股定理得MN===2.1,∴
CN=CM+MN=7.5+2.1=9.6,∴在Rt△ACN中,sin∠CAN===.
20.解:小水塘会影响公路的修建,理由如下:如下图,过点C作CD⊥AB于点D,设CD=x,在Rt△CDB中,∠CDB=90°,∠CBD=45°,tan∠CBD=,∴BD==x,在Rt△CDA中,∠CDA=90°,∠CAD=30°,tan∠CAD=,∴AD==x,又AB=AD+BD=2,∴x+x=2,解得x=-1,∵-1≈0.732<0.8,小水塘会影响公路的修建.
21.解:如下图,过点C作CF⊥AB于点F,∵∠ADC=90°-60°=30°,∠ACD=90°-30°=60°,∴∠CAD=90°,∵CD=10,∴AC=CD=5,在Rt△ACF中,AF=ACsin30°=5×=,CF=ACcos30°=5×=,在Rt△BCF中,∵∠BCF=45°,BF=ACtan30°=5×=,∴AB=AF+BF=+≈9(m).答:景观石AB的高度约为9m.
22.解:(1)如下图,过点A作AQ⊥BC于点Q,过点F作FP⊥BC于点P,则AF=PQ=1,AQ=FP=6,在Rt△ABQ中,∠ABQ=45°,tan∠ABQ=,∴BQ==6,∴BP=BQ-PQ=6-1=5,在Rt△EFP中,i=1︰2=,∴EP=2FP=12,∴EB=EP-BP=12-5=7;www-2-1-cnjy-com
(2)S梯形AFEB=(FA+EB)×FP=(1+7)×6=24,24×300=7200(m3)∴完成这项工程需要土石7200立方米.
23.解:(1)测量示意图如下图;测量步骤:①用皮尺测出测角仪的高度h;②在地面上选择点C安装测角仪并测出此时树顶A点的仰角∠ADE=;③沿CB前进到点F,用皮尺测出点C、F之间的距离CF=l;④在点F处安装测角仪,测得此时树顶A点的仰角∠AGE=.2-1-c-n-j-y
(2)观察测量示意图,设AE=x,在Rt△ADE中,tan∠ADE=,∴DE=-,在Rt△AGE中,tan∠AGE=,∴GE=,∵DE-GE=DG=CF=l,∴=l,解得x=,∴AB=AE+EB=AE+CD=+h.
