4.2.2等差数列的前n项和公式 课件(共37张PPT)-高中数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 4.2.2等差数列的前n项和公式 课件(共37张PPT)-高中数学人教A版(2019)选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 14:54:57 | ||
图片预览










文档简介
(共37张PPT)
4.2.2 等差数列的前n项和公式
新课引入
高斯(Gauss, 1777-1855),德国著名数学家、物理学家、天文学家,近代数学奠基者之一,并享有"数学王子"之称.他和阿基米德、牛顿、欧拉并列为世界四大数学家.
新课引入
据说,200多年前,高斯的算术老师提出了下面的问题:
1+2+3+…+100=?
当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面的方法迅速算出了正确答案:
高斯的算法实际上解决了求等差数列
1, 2, 3, …, n, …
前100项和的问题。
首尾配对相加法
课堂探究
在问题中高斯运用的是“首尾配对”的方法,它使不同数求和问题转化为相同数(即101)的求和,从而简化运算.
思考:高斯在求和过程中利用了数列的什么性质?你能从中得出求数列的前n项和的方法吗?
设an=n,那么高斯的计算方法可以表示为
可以发现,高斯在计算中利用了
探索新知
问题呈现:传说印度泰姬陵的陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见右图),奢靡之程度,可见一斑. 你知道这个图案一共花了多少宝石吗?
探索新知
1
2
3
21
21
20
19
1
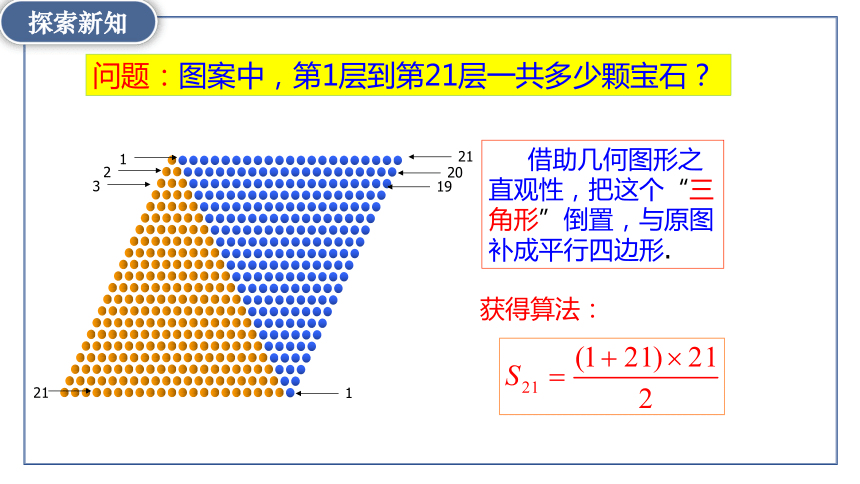
获得算法:
问题:图案中,第1层到第21层一共多少颗宝石?
借助几何图形之直观性,把这个“三角形”倒置,与原图补成平行四边形.
新课讲解
这种方法不需分奇、偶个项的情况就可以求和,很有创意,用数学式子表示就是:
1+ 2+ 3+ 4+……+21
21+20+19+18+……+1
对齐相加(其中第二行的式子与第一行的式子恰好是倒序)
倒序相加法
说明:这实质上是我们数学中一种求和的重要方法.
新课讲解
①
倒序相加法
受此启发,我们得到下面的方法
②
将上述两式相加,可得
新课讲解
已知等差数列{an}的首项为a1, 项数是n, 第n项为an, 求前n项和Sn .
①
②
倒序相加法
思考:那么,对一般的等差数列,如何求它的前n项和呢?
新课讲解
如果等差数列{an}的首项a1, 公差为d, 那么该等差数列的前n项和公式为
注意:等差数列的通项公式和前n项和公式中,共有“a1, d, n, an, Sn”五个量,故知三求二.
把等差数列的通项公式an=a1+(n-1)d带入上式,得
等差数列的前项和n公式:
新课讲解
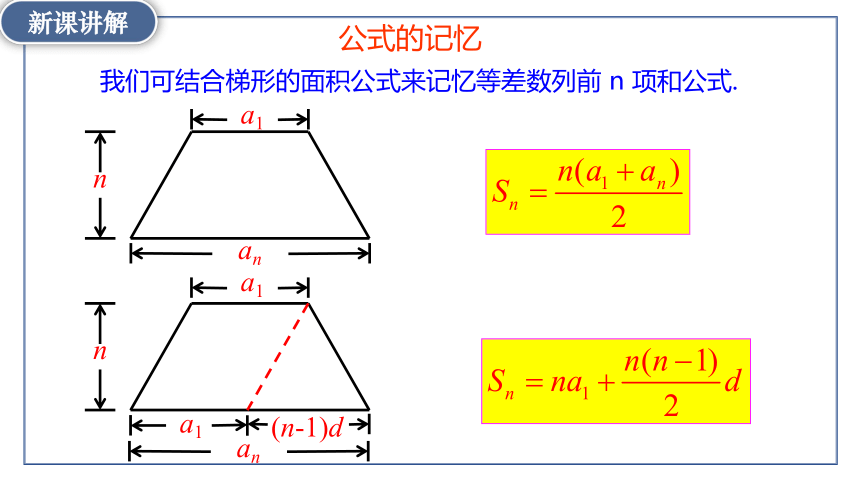
公式的记忆
我们可结合梯形的面积公式来记忆等差数列前 n 项和公式.
a1
(n-1)d
n
a1
an
n
a1
an
典型例题
例1已知数列{an}是等差数列.
(1)若a1=7, a50=101, 求S50; (2)若a1=2, a2=, 求S10;
(3)若a1=, d= - , Sn = -5, 求n.
解: (1)
(2) --2=
+d
2+
整理,得
-7n-60=0
(3)+d, 得
n+
解得n=12或n=-5(舍去)
所以n=12
典型例题
例2 已知一个等差数列的前10项和是310,前 20项和是1220,求该数列的前n项和.
解: 记该数列为{an},公差为d,
根据等差数列前n项和公式,可得
因此该等差数列的前n项和为
解得
巩固训练
1.根据下列各题中的条件,求相应等差数列{an}的前n项和Sn.
(1) a1=5, an=95, n=10;
(2) a1=100, d=-2, n=50;
(3) a1=-4, a8=-18, n=10;
(4) a1=14.5, d=0.7, an=32.
S10=500
S50=2550
S10=-130
S26=604.5
巩固训练
2. 等差数列-1,-3,-5,…的前多少项的和是-100?
10
S16=72
k=16
3. 在等差数列{an}中, Sn为其前n项的和,若S4=6, S8=20,求S16.
4. 在等差数列{an}中, 若S15=5(a2+ a6 + ak),求k.
课堂小结
1.等差数列前n项和的公式;
(两个)
3.在两个求和公式中, 各有五个元素, 只要知道其中三个元素, 结合通项公式就可求出另两个元素——知三求二.
2.等差数列前n项和公式的推导方法——倒序相加法;
本节课你有哪些收获?请做一下总结!
小结
4.2.2 等差数列的前n项和公式
第二课时 等差数列的前n项和公式的性质
新课讲解
(1)当a1>0,d<0时,数列前面有若干项为正, 此时所有正项的和为Sn的最大值. 此时由an≥0且an+1≤0求n的值;
(2)当a1<0,d>0时,数列前面有若干项为负, 此时所有负项的和为Sn的最小值. 此时由an≤0 且an+1 ≥ 0求n的值;
注意:当数列的项中有数值为0时,n应有两解.
求等差数列{an}的前n项和Sn的最值的方法
1.前n项和公式法
2.通项公式法
利用Sn=An2+Bn进行配方,求二次函数的最值,
此时n应取最接近 的正整数值;
利用等差数列的增减性及an的符号变化
探索新知
探究一:如果数列{an}的前n项和为Sn=pn2+qn+r,其中p, q, r为常数,且p≠0,那么这个数列一定是等差数列吗?若是,则它的首项与公差分别是什么?
证:当n≥2时,
当n=1时,a1=S1=p+q+r
当且仅当r =0时,a1满足an=2pn-p+q,此时该数列是等差数列.
an =Sn-Sn-1=pn2+qn+r-p(n-1)2-q(n-1)-r
=2pn-p+q
当r ≠0时,a1不满足an=2pn-p+q,此时数列不是等差数列.
故只有当r=0时该数列才是等差数列, 其中首项a1=p+q, 公差d=2p(p≠0).
性质1:数列{an}是等差数列Sn=An2+Bn (A,B为常数)
小试牛刀
1.已知等差数列{an}的n项和为Sn,且S10=310,S20=1220,求S30.
小试牛刀
2.已知数列{an}的n项和为 ,求数列{an}的通项公式.
解:当n ≥2时,
当n =1时,
,不满足上式
故数列{an}的通项公式为
课堂探究
证明:
探究二:
性质2
小试牛刀
1.已知等差数列{an}的n项和为Sn,且S10=310,S20=1220,求S30.
探究新知
证明:
探究三:
性质3
小试牛刀
1.已知等差数列{an}的n项和为Sn,且S10=310,S20=1220,求S30.
小试牛刀
2. 在等差数列{an}中,已知第1项到第10项的和为310,第11项到第20项的和为910,求第21项到第30项的和.
解:∵数列S10, S20-S10, S30-S20构成等差数列.
∴ 2×910 = 310+ (S30-S20)
∴ S30-S20 = 1510
故第21项到第30项的和为1510.
探索新知
证明:
当m=n时,公式变化?
探究四:
性质4
小试牛刀
2.设等差数列的前n项和为. 若 ,则 _______;
3.设等差数列的前n项和为. 若 ,则 _____;
探索新知
证明:
探究五:
性质5
小试牛刀
1.一个等差数列的前12项和为354,前12项中偶数项和与
奇数项和之比为32∶27,则公差d =______.
解:由条件 ,解得
∴ 由 得
探索新知
证明:
探究六:
性质6
小试牛刀
课堂小结
性质3: 若数列{an}是公差为d的等差数列, 则数列Sm, S2m-Sm, S3m-S2m构成等差数列,且公差为m2d.
性质1:数列{an}是等差数列Sn=An2+Bn (A,B为常数)
性质2: 若数列{an}是公差为d的等差数列, 则数列 也是等差数列, 且公差为 .
等差数列的前n项和公式的性质
性质4:
当m=n时,
课堂小结
等差数列的前n项和公式的性质
性质5:
性质6:
本节课你有哪些收获?请做一下总结!
小结
4.2.2 等差数列的前n项和公式
新课引入
高斯(Gauss, 1777-1855),德国著名数学家、物理学家、天文学家,近代数学奠基者之一,并享有"数学王子"之称.他和阿基米德、牛顿、欧拉并列为世界四大数学家.
新课引入
据说,200多年前,高斯的算术老师提出了下面的问题:
1+2+3+…+100=?
当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面的方法迅速算出了正确答案:
高斯的算法实际上解决了求等差数列
1, 2, 3, …, n, …
前100项和的问题。
首尾配对相加法
课堂探究
在问题中高斯运用的是“首尾配对”的方法,它使不同数求和问题转化为相同数(即101)的求和,从而简化运算.
思考:高斯在求和过程中利用了数列的什么性质?你能从中得出求数列的前n项和的方法吗?
设an=n,那么高斯的计算方法可以表示为
可以发现,高斯在计算中利用了
探索新知
问题呈现:传说印度泰姬陵的陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见右图),奢靡之程度,可见一斑. 你知道这个图案一共花了多少宝石吗?
探索新知
1
2
3
21
21
20
19
1
获得算法:
问题:图案中,第1层到第21层一共多少颗宝石?
借助几何图形之直观性,把这个“三角形”倒置,与原图补成平行四边形.
新课讲解
这种方法不需分奇、偶个项的情况就可以求和,很有创意,用数学式子表示就是:
1+ 2+ 3+ 4+……+21
21+20+19+18+……+1
对齐相加(其中第二行的式子与第一行的式子恰好是倒序)
倒序相加法
说明:这实质上是我们数学中一种求和的重要方法.
新课讲解
①
倒序相加法
受此启发,我们得到下面的方法
②
将上述两式相加,可得
新课讲解
已知等差数列{an}的首项为a1, 项数是n, 第n项为an, 求前n项和Sn .
①
②
倒序相加法
思考:那么,对一般的等差数列,如何求它的前n项和呢?
新课讲解
如果等差数列{an}的首项a1, 公差为d, 那么该等差数列的前n项和公式为
注意:等差数列的通项公式和前n项和公式中,共有“a1, d, n, an, Sn”五个量,故知三求二.
把等差数列的通项公式an=a1+(n-1)d带入上式,得
等差数列的前项和n公式:
新课讲解
公式的记忆
我们可结合梯形的面积公式来记忆等差数列前 n 项和公式.
a1
(n-1)d
n
a1
an
n
a1
an
典型例题
例1已知数列{an}是等差数列.
(1)若a1=7, a50=101, 求S50; (2)若a1=2, a2=, 求S10;
(3)若a1=, d= - , Sn = -5, 求n.
解: (1)
(2) --2=
+d
2+
整理,得
-7n-60=0
(3)+d, 得
n+
解得n=12或n=-5(舍去)
所以n=12
典型例题
例2 已知一个等差数列的前10项和是310,前 20项和是1220,求该数列的前n项和.
解: 记该数列为{an},公差为d,
根据等差数列前n项和公式,可得
因此该等差数列的前n项和为
解得
巩固训练
1.根据下列各题中的条件,求相应等差数列{an}的前n项和Sn.
(1) a1=5, an=95, n=10;
(2) a1=100, d=-2, n=50;
(3) a1=-4, a8=-18, n=10;
(4) a1=14.5, d=0.7, an=32.
S10=500
S50=2550
S10=-130
S26=604.5
巩固训练
2. 等差数列-1,-3,-5,…的前多少项的和是-100?
10
S16=72
k=16
3. 在等差数列{an}中, Sn为其前n项的和,若S4=6, S8=20,求S16.
4. 在等差数列{an}中, 若S15=5(a2+ a6 + ak),求k.
课堂小结
1.等差数列前n项和的公式;
(两个)
3.在两个求和公式中, 各有五个元素, 只要知道其中三个元素, 结合通项公式就可求出另两个元素——知三求二.
2.等差数列前n项和公式的推导方法——倒序相加法;
本节课你有哪些收获?请做一下总结!
小结
4.2.2 等差数列的前n项和公式
第二课时 等差数列的前n项和公式的性质
新课讲解
(1)当a1>0,d<0时,数列前面有若干项为正, 此时所有正项的和为Sn的最大值. 此时由an≥0且an+1≤0求n的值;
(2)当a1<0,d>0时,数列前面有若干项为负, 此时所有负项的和为Sn的最小值. 此时由an≤0 且an+1 ≥ 0求n的值;
注意:当数列的项中有数值为0时,n应有两解.
求等差数列{an}的前n项和Sn的最值的方法
1.前n项和公式法
2.通项公式法
利用Sn=An2+Bn进行配方,求二次函数的最值,
此时n应取最接近 的正整数值;
利用等差数列的增减性及an的符号变化
探索新知
探究一:如果数列{an}的前n项和为Sn=pn2+qn+r,其中p, q, r为常数,且p≠0,那么这个数列一定是等差数列吗?若是,则它的首项与公差分别是什么?
证:当n≥2时,
当n=1时,a1=S1=p+q+r
当且仅当r =0时,a1满足an=2pn-p+q,此时该数列是等差数列.
an =Sn-Sn-1=pn2+qn+r-p(n-1)2-q(n-1)-r
=2pn-p+q
当r ≠0时,a1不满足an=2pn-p+q,此时数列不是等差数列.
故只有当r=0时该数列才是等差数列, 其中首项a1=p+q, 公差d=2p(p≠0).
性质1:数列{an}是等差数列Sn=An2+Bn (A,B为常数)
小试牛刀
1.已知等差数列{an}的n项和为Sn,且S10=310,S20=1220,求S30.
小试牛刀
2.已知数列{an}的n项和为 ,求数列{an}的通项公式.
解:当n ≥2时,
当n =1时,
,不满足上式
故数列{an}的通项公式为
课堂探究
证明:
探究二:
性质2
小试牛刀
1.已知等差数列{an}的n项和为Sn,且S10=310,S20=1220,求S30.
探究新知
证明:
探究三:
性质3
小试牛刀
1.已知等差数列{an}的n项和为Sn,且S10=310,S20=1220,求S30.
小试牛刀
2. 在等差数列{an}中,已知第1项到第10项的和为310,第11项到第20项的和为910,求第21项到第30项的和.
解:∵数列S10, S20-S10, S30-S20构成等差数列.
∴ 2×910 = 310+ (S30-S20)
∴ S30-S20 = 1510
故第21项到第30项的和为1510.
探索新知
证明:
当m=n时,公式变化?
探究四:
性质4
小试牛刀
2.设等差数列的前n项和为. 若 ,则 _______;
3.设等差数列的前n项和为. 若 ,则 _____;
探索新知
证明:
探究五:
性质5
小试牛刀
1.一个等差数列的前12项和为354,前12项中偶数项和与
奇数项和之比为32∶27,则公差d =______.
解:由条件 ,解得
∴ 由 得
探索新知
证明:
探究六:
性质6
小试牛刀
课堂小结
性质3: 若数列{an}是公差为d的等差数列, 则数列Sm, S2m-Sm, S3m-S2m构成等差数列,且公差为m2d.
性质1:数列{an}是等差数列Sn=An2+Bn (A,B为常数)
性质2: 若数列{an}是公差为d的等差数列, 则数列 也是等差数列, 且公差为 .
等差数列的前n项和公式的性质
性质4:
当m=n时,
课堂小结
等差数列的前n项和公式的性质
性质5:
性质6:
本节课你有哪些收获?请做一下总结!
小结
