4.3.1 等比数列 课件(共45张PPT)-高中数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 4.3.1 等比数列 课件(共45张PPT)-高中数学人教A版(2019)选择性必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 14:57:32 | ||
图片预览









文档简介
(共44张PPT)
4.3.1 等比数列的概念
情景引入
1.两河流域发掘的古巴比伦时期的泥板上记录了下面的数列:
你发现上述数列有什么规律?
情景引入
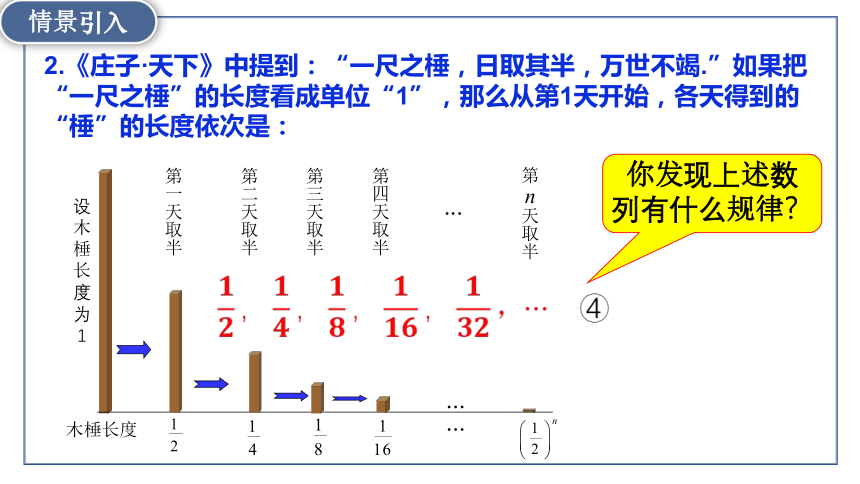
2.《庄子·天下》中提到:“一尺之棰,日取其半,万世不竭.”如果把“一尺之棰”的长度看成单位“1”,那么从第1天开始,各天得到的“棰”的长度依次是:
木棰长度
第一天取半
第二天取半
第三天取半
第四天取半
...
...
...
第 天取半
n
设木棰长度为
1
你发现上述数列有什么规律?
情景引入
细菌个数
第一次
第二次
第三次
2
4
第 n 次
……
分裂次数
8
2n
3.在营养和生存空间没有限制的情况下,某种细菌每20 min就通过分裂繁殖一代,那么一个这种细菌从第1次分裂开始,各次分裂产生的后代个数依次是:
你发现上述数列有什么规律?
课堂探究
思考:请同学们仔细观察以下五个数列, 类比等差数列的研究, 你认为可以通过怎样的运算发现以下数列的取值规律 你发现了什么规律
共同特点: 从第二项起,每一项与前一项的比都等于同一个常数.
如果用{an}表示数列①,那么有
取值规律: 从第 2 项起, 每一项与它的前一项的比都等于 9.
探究新知
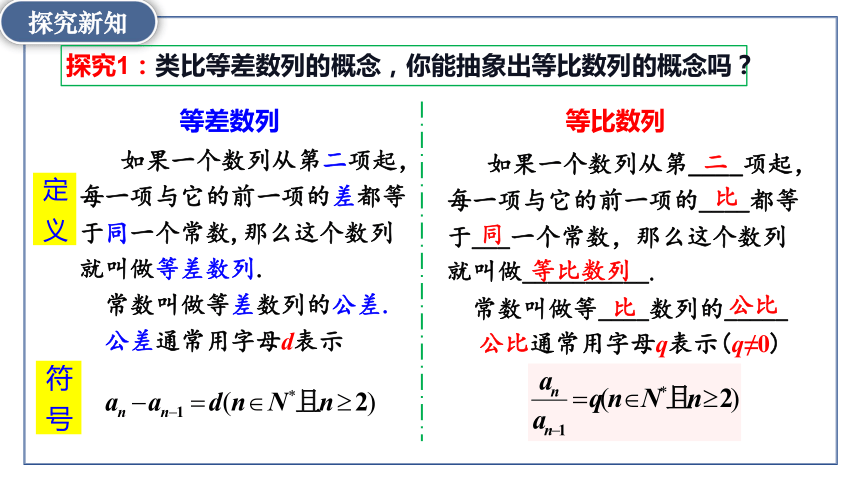
如果一个数列从第____项起,每一项与它的前一项的____都等于___一个常数,那么这个数列就叫做__________.
常数叫做等____数列的_____
等比数列
二
比
同
等比数列
公比
等差数列
如果一个数列从第二项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.
常数叫做等差数列的公差.
公差通常用字母d表示
公比通常用字母q表示(q≠0)
比
探究1:类比等差数列的概念,你能抽象出等比数列的概念吗?
定义
符号
小试牛刀
(3) 5, 5, 5, 5, 5, 5,…
1.观察并判断下列数列是否是等比数列,是的话,指出公比,不是的话请说明理由:
(4) 0, 1, 2, 4, 8, …
(5) 2, 0, 2, 0, 2, …
是,公比是 2
是,公比是 -2
是,公比是 1
不一定,分类讨论
不是,分母不能为 0
不是,公比不能是 0
探索新知
思考1:等差数列的项、公差均可以是0吗?等比数列呢?
思考2:常数列是等差数列吗?是等比数列吗?
思考3:是否存在既是等差数列又是等比数列的数列?
常数列一定是等差数列,公差为0;
非零常数列是等比数列,公比为1.
非零常数列既是等差数列又是等比数列, 公差为0, 公比为1.
等差数列的项、公差均可以是0,
但等比数列的项和公比均不可以是0
探究新知
等差中项
等比中项
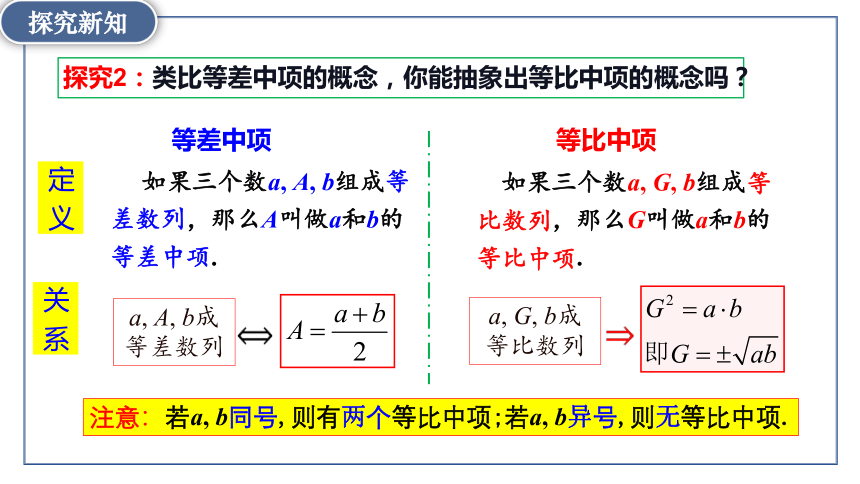
如果三个数a, A, b组成等差数列,那么A叫做a和b的等差中项.
如果三个数a, G, b组成等比数列,那么G叫做a和b的等比中项.
定义
a, A, b成等差数列
a, G, b成等比数列
关系
注意:若a, b同号,则有两个等比中项;若a, b异号,则无等比中项.
探究2:类比等差中项的概念,你能抽象出等比中项的概念吗?
探究新知
探究3:类比等差数列的通项公式,你能根据等比数列的定义推导它的通项公式吗?
等差数列
等比数列
不完全归纳法
探究新知
累乘法
累加法
等差数列
等比数列
探究新知
等比数列的通项公式:
思考:已知等比数列的第 m 项 am,公比为 q, 求通项公式 an.
等比数列的任意一项都可以由该数列的某一项和公比表示.
探索新知
指数型函数
思考1:类比指数函数的性质,判断公比q>0的等比数列的单调性?
探究4:类比等差数列与一次函数的关系,等比数列可以与哪类函数建立关系?
q
q>1
0a1>0
a1<0
q=1
a1
探究新知
从图象上看,表示等比数列{an} 中的各项的点是指数型函数 图象上一群孤立的点.
思考2:公比q>0且q≠1的等比数列的图象有什么特点?
典型例题
例1 若等比数列的第4项和第6项分别为48和12, 求的第5项.
解法1:
②的两边分别除以①的两边,得
解得
把代入①,得
此时==384=24
把代入②,得
此时==-384=-24
因此,的第5项是24或-24
两个,需对其分类讨论
由,得
①
②
典型例题
解法2:
因为是和的等比中项,所以
因此,的第5项是24或-24
==
所以
例1 若等比数列的第4项和第6项分别为48和12, 求的第5项.
变式练习:若48和12分别是第4项和第8项,求第6项.
注意:等比中项还要关注项的关系,奇数项的符号相同,偶数项的符号相同.
典型例题
例2 数列共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132.求这个数列.
解:
设前三项的公比为,后三项的公差为,则数列的各项依次为
,,80,80+,80+2. 于是得
解得
所以这个数列是20,40,80,96,112或180,120,80,16,-48
注意设法
方法归纳
(1)如果是三个数成等比数列,可设为 ,a,aq
对称设元法
(2)如果是四个数成等比数列,可设为 , ,aq,aq3
1.与等差数列有关的数的设元技巧:
2.与等比数列有关的数的设元技巧:
(1)如果是三个数成等差数列,可设为a - d,a, a+d
(2)如果是四个数成等差数列,可设为a+2d , a - d , a+d , a+2d
巩固训练
1.已知四个数,前三个数成等差数列,后三个数成等比数列,中间两个之积为16,前后两个数之积为-128.求这四个数.
解:设所求四个数为
由题意知
解得
因此所求的四个数为-4,2,8,32或4,-2,-8,-32.
课堂小结
形
等差数列
等比数列
类比
抽象概念
代数运算
归纳法
累乘法
累加法
通项公式
函数角度
数
一次函数
指数函数
数
形
小结
本节课你有哪些收获?请做一下总结!
4.3.1 等比数列的概念
第二课时 等比数列的性质
复习引入
1.等比数列
2. 通项公式
4.等比数列的判断
3. 等比中项
(an)2=an-1.an+1
a,G,b成等比数列
探究新知
即:下标和相等,对应项的和相等
注意:等号两侧的项数必须相同
即:下标和相等,对应项的积相等
探究新知
(2)在有穷数列中,与首末两项“等距离”的两项之和等于首末两项的和
(2)在有穷数列中,与首末两项“等距离”的两项之积等于首末两项的积
等差数列:
等比数列:
小试牛刀
1.已知{an}是一个等比数列,请在下表中的空格处填入适当的数.
a1 a3 a5 a7 q
2 8
2 0.2
50
0.08
0.0032
4
16
2.已知等比数列{an}中,a1a3=36,a2+a4=60.求a1和公比q.
a1=2,q=3或a1=-2,q=-3
小试牛刀
512
6
20
典型例题
例1 用10 000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获利多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息.(精确到)
月初本金 月末本利和
1个月
2个月
3个月
12个月
典型例题
例1 用10 000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获利多少利息(精确到1元)?
解:
(1)设这笔钱存个月以后的本利和组成一个数列则是等比数列.
首项
公比
所以,
所以,12个月后的利息为10490.97-10000491(元)
利息=本利和-本金
典型例题
设季度利率为,这笔钱存个季度以后的本利和组成一个数列,则也是一个等比数列,
解:
首项
所以,
因此,以季度复利计息,存4个季度后的利息为元
解不等式,得
所以,当季度利率不小于时,按季结算的利息不少于按月结算的利息.
例1 用10 000元购买某个理财产品一年.
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息.(精确到)
巩固训练
典型例题
例2 已知数列的首项
(1)若数列为等差数列,公差=2,证明数列为等比数列;
(2)若数列为等比数列,公比=,证明数列为等差数列.
分析:如何证明一个数列为等差数列或者等比数列
等差数列:
等比数列:
利用定义
先求
通项公式
典型例题
证明:
(1)由=2,得的通项公式为
设,则
又
所以是以27为首项,9为公比的等比数列
(2)由, =,得的通项公式为
所以是首项为1,公差为-2的等差数列
两边取以3为底的对数,得
又
区分两问的求法有何不同
探究新知
思考:
性质1:数列{an}是等差数列 数列 是等比数列.
性质2:数列{an}是正项等比数列 数列{logban}是等差数列.
巩固训练
1.若{an}, {bn}是项数相同的等比数列, 且公比分别为q, q′的, c为常数, 则下列数列是等比数列吗?若是,公比是什么?
(1){} ; (2){} ; (3){c} ;
(4){+c} ; (5){· } ;
(6){} ; (7){} ;
(8){} ; (9){}.
√
√
√
√
√
√
√
等比
2.若2a,2b,2c成等比数列,则a, b, c成 数列.
等差
3.若lga, lgb, lgc成等差数列,则a, b, c成 数列.
归纳小结
典型例题
例3 某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品。1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
产量
不合格率
数列
数列
等比数列
等差数列
分析:
不合格品
产量×不合格率
等差数列×等比数列
典型例题
解:
设从今年1月起,每个月的产量和不合格率分别构成数列,
由题意,知
,其中=1,2,,24
从今年1月起,各月不合格产品的数量是
由计算工具计算(精确到0.1),并列表.
典型例题
观察发现,数列先递增,在第6项以后递减,所以只要设法证明当时,递减,且即可.
所以,当时,递减
又
所以,当时,
所以,生产该产品一年后,月不合格品的数量能控制在100个以内.
巩固训练
巩固训练
解:(1)
巩固训练
课堂小结
等差数列 等比数列
定义
通项公式
中项
性质
an+1-an=d
an = a1 +(n-1)d
等差数列与等比数列的类比
本节课你有哪些收获?请做一下总结!
小结
4.3.1 等比数列的概念
情景引入
1.两河流域发掘的古巴比伦时期的泥板上记录了下面的数列:
你发现上述数列有什么规律?
情景引入
2.《庄子·天下》中提到:“一尺之棰,日取其半,万世不竭.”如果把“一尺之棰”的长度看成单位“1”,那么从第1天开始,各天得到的“棰”的长度依次是:
木棰长度
第一天取半
第二天取半
第三天取半
第四天取半
...
...
...
第 天取半
n
设木棰长度为
1
你发现上述数列有什么规律?
情景引入
细菌个数
第一次
第二次
第三次
2
4
第 n 次
……
分裂次数
8
2n
3.在营养和生存空间没有限制的情况下,某种细菌每20 min就通过分裂繁殖一代,那么一个这种细菌从第1次分裂开始,各次分裂产生的后代个数依次是:
你发现上述数列有什么规律?
课堂探究
思考:请同学们仔细观察以下五个数列, 类比等差数列的研究, 你认为可以通过怎样的运算发现以下数列的取值规律 你发现了什么规律
共同特点: 从第二项起,每一项与前一项的比都等于同一个常数.
如果用{an}表示数列①,那么有
取值规律: 从第 2 项起, 每一项与它的前一项的比都等于 9.
探究新知
如果一个数列从第____项起,每一项与它的前一项的____都等于___一个常数,那么这个数列就叫做__________.
常数叫做等____数列的_____
等比数列
二
比
同
等比数列
公比
等差数列
如果一个数列从第二项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.
常数叫做等差数列的公差.
公差通常用字母d表示
公比通常用字母q表示(q≠0)
比
探究1:类比等差数列的概念,你能抽象出等比数列的概念吗?
定义
符号
小试牛刀
(3) 5, 5, 5, 5, 5, 5,…
1.观察并判断下列数列是否是等比数列,是的话,指出公比,不是的话请说明理由:
(4) 0, 1, 2, 4, 8, …
(5) 2, 0, 2, 0, 2, …
是,公比是 2
是,公比是 -2
是,公比是 1
不一定,分类讨论
不是,分母不能为 0
不是,公比不能是 0
探索新知
思考1:等差数列的项、公差均可以是0吗?等比数列呢?
思考2:常数列是等差数列吗?是等比数列吗?
思考3:是否存在既是等差数列又是等比数列的数列?
常数列一定是等差数列,公差为0;
非零常数列是等比数列,公比为1.
非零常数列既是等差数列又是等比数列, 公差为0, 公比为1.
等差数列的项、公差均可以是0,
但等比数列的项和公比均不可以是0
探究新知
等差中项
等比中项
如果三个数a, A, b组成等差数列,那么A叫做a和b的等差中项.
如果三个数a, G, b组成等比数列,那么G叫做a和b的等比中项.
定义
a, A, b成等差数列
a, G, b成等比数列
关系
注意:若a, b同号,则有两个等比中项;若a, b异号,则无等比中项.
探究2:类比等差中项的概念,你能抽象出等比中项的概念吗?
探究新知
探究3:类比等差数列的通项公式,你能根据等比数列的定义推导它的通项公式吗?
等差数列
等比数列
不完全归纳法
探究新知
累乘法
累加法
等差数列
等比数列
探究新知
等比数列的通项公式:
思考:已知等比数列的第 m 项 am,公比为 q, 求通项公式 an.
等比数列的任意一项都可以由该数列的某一项和公比表示.
探索新知
指数型函数
思考1:类比指数函数的性质,判断公比q>0的等比数列的单调性?
探究4:类比等差数列与一次函数的关系,等比数列可以与哪类函数建立关系?
q
q>1
0
a1<0
q=1
a1
探究新知
从图象上看,表示等比数列{an} 中的各项的点是指数型函数 图象上一群孤立的点.
思考2:公比q>0且q≠1的等比数列的图象有什么特点?
典型例题
例1 若等比数列的第4项和第6项分别为48和12, 求的第5项.
解法1:
②的两边分别除以①的两边,得
解得
把代入①,得
此时==384=24
把代入②,得
此时==-384=-24
因此,的第5项是24或-24
两个,需对其分类讨论
由,得
①
②
典型例题
解法2:
因为是和的等比中项,所以
因此,的第5项是24或-24
==
所以
例1 若等比数列的第4项和第6项分别为48和12, 求的第5项.
变式练习:若48和12分别是第4项和第8项,求第6项.
注意:等比中项还要关注项的关系,奇数项的符号相同,偶数项的符号相同.
典型例题
例2 数列共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132.求这个数列.
解:
设前三项的公比为,后三项的公差为,则数列的各项依次为
,,80,80+,80+2. 于是得
解得
所以这个数列是20,40,80,96,112或180,120,80,16,-48
注意设法
方法归纳
(1)如果是三个数成等比数列,可设为 ,a,aq
对称设元法
(2)如果是四个数成等比数列,可设为 , ,aq,aq3
1.与等差数列有关的数的设元技巧:
2.与等比数列有关的数的设元技巧:
(1)如果是三个数成等差数列,可设为a - d,a, a+d
(2)如果是四个数成等差数列,可设为a+2d , a - d , a+d , a+2d
巩固训练
1.已知四个数,前三个数成等差数列,后三个数成等比数列,中间两个之积为16,前后两个数之积为-128.求这四个数.
解:设所求四个数为
由题意知
解得
因此所求的四个数为-4,2,8,32或4,-2,-8,-32.
课堂小结
形
等差数列
等比数列
类比
抽象概念
代数运算
归纳法
累乘法
累加法
通项公式
函数角度
数
一次函数
指数函数
数
形
小结
本节课你有哪些收获?请做一下总结!
4.3.1 等比数列的概念
第二课时 等比数列的性质
复习引入
1.等比数列
2. 通项公式
4.等比数列的判断
3. 等比中项
(an)2=an-1.an+1
a,G,b成等比数列
探究新知
即:下标和相等,对应项的和相等
注意:等号两侧的项数必须相同
即:下标和相等,对应项的积相等
探究新知
(2)在有穷数列中,与首末两项“等距离”的两项之和等于首末两项的和
(2)在有穷数列中,与首末两项“等距离”的两项之积等于首末两项的积
等差数列:
等比数列:
小试牛刀
1.已知{an}是一个等比数列,请在下表中的空格处填入适当的数.
a1 a3 a5 a7 q
2 8
2 0.2
50
0.08
0.0032
4
16
2.已知等比数列{an}中,a1a3=36,a2+a4=60.求a1和公比q.
a1=2,q=3或a1=-2,q=-3
小试牛刀
512
6
20
典型例题
例1 用10 000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获利多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息.(精确到)
月初本金 月末本利和
1个月
2个月
3个月
12个月
典型例题
例1 用10 000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获利多少利息(精确到1元)?
解:
(1)设这笔钱存个月以后的本利和组成一个数列则是等比数列.
首项
公比
所以,
所以,12个月后的利息为10490.97-10000491(元)
利息=本利和-本金
典型例题
设季度利率为,这笔钱存个季度以后的本利和组成一个数列,则也是一个等比数列,
解:
首项
所以,
因此,以季度复利计息,存4个季度后的利息为元
解不等式,得
所以,当季度利率不小于时,按季结算的利息不少于按月结算的利息.
例1 用10 000元购买某个理财产品一年.
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息.(精确到)
巩固训练
典型例题
例2 已知数列的首项
(1)若数列为等差数列,公差=2,证明数列为等比数列;
(2)若数列为等比数列,公比=,证明数列为等差数列.
分析:如何证明一个数列为等差数列或者等比数列
等差数列:
等比数列:
利用定义
先求
通项公式
典型例题
证明:
(1)由=2,得的通项公式为
设,则
又
所以是以27为首项,9为公比的等比数列
(2)由, =,得的通项公式为
所以是首项为1,公差为-2的等差数列
两边取以3为底的对数,得
又
区分两问的求法有何不同
探究新知
思考:
性质1:数列{an}是等差数列 数列 是等比数列.
性质2:数列{an}是正项等比数列 数列{logban}是等差数列.
巩固训练
1.若{an}, {bn}是项数相同的等比数列, 且公比分别为q, q′的, c为常数, 则下列数列是等比数列吗?若是,公比是什么?
(1){} ; (2){} ; (3){c} ;
(4){+c} ; (5){· } ;
(6){} ; (7){} ;
(8){} ; (9){}.
√
√
√
√
√
√
√
等比
2.若2a,2b,2c成等比数列,则a, b, c成 数列.
等差
3.若lga, lgb, lgc成等差数列,则a, b, c成 数列.
归纳小结
典型例题
例3 某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品。1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
产量
不合格率
数列
数列
等比数列
等差数列
分析:
不合格品
产量×不合格率
等差数列×等比数列
典型例题
解:
设从今年1月起,每个月的产量和不合格率分别构成数列,
由题意,知
,其中=1,2,,24
从今年1月起,各月不合格产品的数量是
由计算工具计算(精确到0.1),并列表.
典型例题
观察发现,数列先递增,在第6项以后递减,所以只要设法证明当时,递减,且即可.
所以,当时,递减
又
所以,当时,
所以,生产该产品一年后,月不合格品的数量能控制在100个以内.
巩固训练
巩固训练
解:(1)
巩固训练
课堂小结
等差数列 等比数列
定义
通项公式
中项
性质
an+1-an=d
an = a1 +(n-1)d
等差数列与等比数列的类比
本节课你有哪些收获?请做一下总结!
小结
