4.3.3数列求和微专题 课件(共35张PPT)-高中数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 4.3.3数列求和微专题 课件(共35张PPT)-高中数学人教A版(2019)选择性必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 15:06:33 | ||
图片预览











文档简介
(共35张PPT)
4.3 数列求和
微专题
新课讲解
2.等比数列前n项和公式(错位相减法)
1.等差数列前n项和公式(倒序相加法)
一、公式法
3.两类特殊数列的前n项和(二次幂和、三次幂和)
典型例题
例1 数列{an}满足an =3n-20,求数列{an}的前n项和Sn的最小值.
当n=6时,数列{an}的前n项和Sn最小,且
新课讲解
(1)倒序相加法是推导等差数列的前n项和公式时所用的方法,就是将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n个(a1+an).
(2)如果一个数列{an},首末两端等“距离”的两项的和相等,那么求其和可以用倒序相加法.
二、倒序相加法
典型例题
例2 已知函数y=f(x)满足f(x) + f(1-x) =1,若数列{an}满足
,求数列{an}的前20项和.
巩固训练
新课讲解
(1)使用条件:
①通项公式是形如an·bn的形式,
②数列{an}和{bn}中一个是等差数列, 一个是等比数列;
(2)所乘系数: 在等式两边同乘的是等比数列的公比;
(3)书写格式: 两个等式中次数一样的项对齐;
(4)差的特点: 相减后的差共有n+1项, 去掉前后两项,
中间的n-1项一定是等比数列.
三、错位相减法
典型例题
例3 已知数列{an}的前n项和为Sn,且a1 =2,Sn = an+1-2,求数列{(2n+1)an}的前n项和Tn.
典型例题
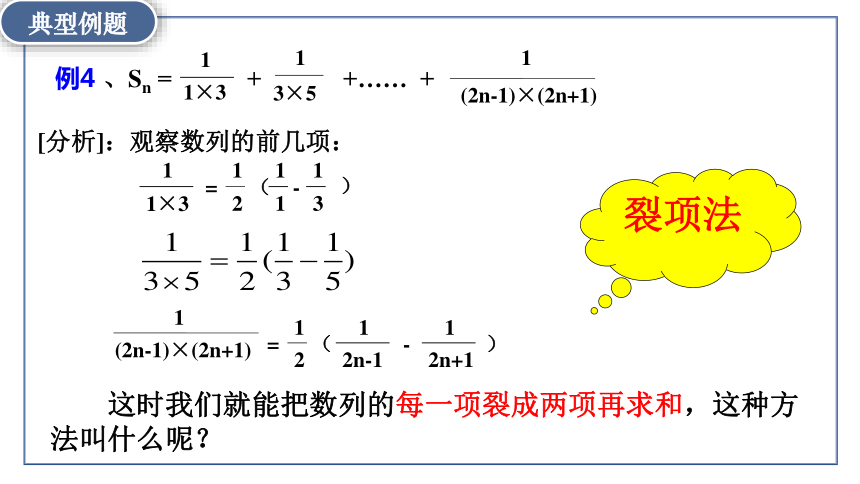
例4 、Sn = + +…… +
1
1×3
1
3×5
1
(2n-1)×(2n+1)
[分析]:观察数列的前几项:
1
(2n-1)×(2n+1)
= ( - )
2
1
2n-1
1
2n+1
1
这时我们就能把数列的每一项裂成两项再求和,这种方法叫什么呢?
裂项法
1
1×3
= ( -
2
1
3
1
1
1
)
典型例题
解:由通项an=
1
(2n-1)×(2n+1)
= ( - )
2
1
2n-1
1
2n+1
1
∴Sn=
( - + - +……+ - )
2
1
3
1
1
1
5
1
3
1
2n-1
1
2n+1
1
= (1 - )
2
1
2n+1
1
2n+1
n
=
评:裂项相消法的关键就是将数列的每一项拆成二项或多项使数列中的项出现有规律的抵消项,进而达到求和的目的。
四、裂项相消法
例4 、Sn = + +…… +
1
1×3
1
3×5
1
(2n-1)×(2n+1)
巩固训练
新课讲解
通项公式为分式,可用待定系数法对通项公式拆项.
四、裂项相消法
典型例题
例4 已知数列 是公比为4的等比数列,且满足a2, a4, a7成等比数列,求数列 的前n项和Tn.
变式训练
2.在数列{an}中,
,求数列{bn}的前n项的和.
变式训练
新课讲解
(1)一般情况下形如cn=an±bn ;
(2)数列{an}与{bn}是等差数列, 或等比数列, 或是其他已知求和方法的数列;
(3)求数列{cn}的前n项和,分别利用已知的求和方法;
如等差数列和等比数列前n项和公式求和即可.
五、分组求和法
典型例题
例5 已知数列{an}满足an =3an-1+2(n≥2),a1 =1,若bn =3an+2n-1,求数列{bn}的前n项和Tn.
典型例题
新课讲解
2.适用于通项中含有(-1)n的数列[摆动数列] ,形如an=(-1)nf(n),可采用两项合并求解.
3.涉及奇偶问题,则需要讨论n的奇偶性,分项数为奇数和偶数分别进行求和,最后综合.
六、并项求和法
1.求 一个数列的前n项和,可两两结合求解,则称之为并项求和.
典型例题
例6 求12-22+32-42+…+(-1)n-1n2.
七、分类讨论法
新课讲解
新课讲解
八、绝对值型求和
实际就是一个去绝对值的过程, 绝对值的临界值就是分类讨论的点.
已知数列{an}的前n项和为Sn, 求数列{|an|}的前n项和Tn.
思路:由an≥0, 得n≤n0(不妨设为n0整数)
当1≤n≤n0时, an≥0;而当n≥n0+1时, an≤0.
当1≤n≤n0时, Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn
当n≥n0+1时, Tn=|a1|+|a2|+…+|an0|+|an0+1|+…+|an|
=(a1+a2+…+an0)-(an0+1+…+an)
=Sn0-(Sn-Sn0)
=2Sn0-Sn
综上,
典型例题
例8 已知数列{an}的前n项和为Sn=14n-n2,求数列{|an|}的前n项和Tn.
巩固训练
1.求数列1,3+5,7+9+11,13+15+17+19,…的前n项和.
这些奇数组成等差数列,首项为1,公差为2,
故该数列的前n项和
巩固训练
20
巩固训练
解: (1)当x=±1时,Sn=4n.
综上可知,
(2)当x≠±1时,
巩固训练
巩固训练
4.求和:Sn=-1+3-5+7-…+(-1)n(2n-1).
解:当n为奇数时,
Sn=(-1+3)+(-5+7)+(-9+11)+…+[(-2n+5)+(2n-3)]+(-2n+1)
当n为偶数时,
∴Sn=(-1)n·n (n∈N*).
巩固训练
5.求和:Sn=x+2x2+3x3+…+nxn(x≠0).
当x≠1时,Sn=x + 2x2 + 3x3 + 4x4 +…(n-1)xn-1+ nxn,
xSn= x2 + 2x3 + 3x4 +… … +(n-1)xn+nxn+1,
∴(1-x)Sn=x + x2 + x3 + … … … … … + xn -nxn+1
巩固训练
巩固训练
7. 已知等差数列{an}中, 公差d=2, a2是a1和a4的等比中项.设 ,
求数列{bn}的前n项和Tn.
课堂小结
1.公式法
(2)四类特殊数列的前n项和
(1)等差、等比数列的前n项和公式;
求数列前n项和的方法
3.错位相减法
(1)形如cn=an·bn, 一个是等差数列,一个是等比数列;
(2)步骤:乘公比,错位减
(2)数列{an}与首末两端等“距离”的两项和相等,则用倒序相加法求和.
2.倒序相加法
(1)将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n个(a1+an);
4.裂项相消法
(1)通项公式为分式,可用待定系数法对通项公式拆项;
(2)记住常见的拆项公式
课堂小结
(1)适用于通项中含有(-1)n的数列[摆动数列] ;
6.并项求和法
(2)也可分奇数项和偶数项求和
求数列前n项和的方法
8.绝对值型求和
实际就是一个去绝对值的过程, 绝对值的临界值就是分类讨论的点.
5.分组求和法
(2)数列{an}与{bn}是已知求和方法的数列;
(1)一般情况下形如cn=an±bn ;
7.分奇偶讨论
本节课你有哪些收获?请做一下总结!
小结
4.3 数列求和
微专题
新课讲解
2.等比数列前n项和公式(错位相减法)
1.等差数列前n项和公式(倒序相加法)
一、公式法
3.两类特殊数列的前n项和(二次幂和、三次幂和)
典型例题
例1 数列{an}满足an =3n-20,求数列{an}的前n项和Sn的最小值.
当n=6时,数列{an}的前n项和Sn最小,且
新课讲解
(1)倒序相加法是推导等差数列的前n项和公式时所用的方法,就是将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n个(a1+an).
(2)如果一个数列{an},首末两端等“距离”的两项的和相等,那么求其和可以用倒序相加法.
二、倒序相加法
典型例题
例2 已知函数y=f(x)满足f(x) + f(1-x) =1,若数列{an}满足
,求数列{an}的前20项和.
巩固训练
新课讲解
(1)使用条件:
①通项公式是形如an·bn的形式,
②数列{an}和{bn}中一个是等差数列, 一个是等比数列;
(2)所乘系数: 在等式两边同乘的是等比数列的公比;
(3)书写格式: 两个等式中次数一样的项对齐;
(4)差的特点: 相减后的差共有n+1项, 去掉前后两项,
中间的n-1项一定是等比数列.
三、错位相减法
典型例题
例3 已知数列{an}的前n项和为Sn,且a1 =2,Sn = an+1-2,求数列{(2n+1)an}的前n项和Tn.
典型例题
例4 、Sn = + +…… +
1
1×3
1
3×5
1
(2n-1)×(2n+1)
[分析]:观察数列的前几项:
1
(2n-1)×(2n+1)
= ( - )
2
1
2n-1
1
2n+1
1
这时我们就能把数列的每一项裂成两项再求和,这种方法叫什么呢?
裂项法
1
1×3
= ( -
2
1
3
1
1
1
)
典型例题
解:由通项an=
1
(2n-1)×(2n+1)
= ( - )
2
1
2n-1
1
2n+1
1
∴Sn=
( - + - +……+ - )
2
1
3
1
1
1
5
1
3
1
2n-1
1
2n+1
1
= (1 - )
2
1
2n+1
1
2n+1
n
=
评:裂项相消法的关键就是将数列的每一项拆成二项或多项使数列中的项出现有规律的抵消项,进而达到求和的目的。
四、裂项相消法
例4 、Sn = + +…… +
1
1×3
1
3×5
1
(2n-1)×(2n+1)
巩固训练
新课讲解
通项公式为分式,可用待定系数法对通项公式拆项.
四、裂项相消法
典型例题
例4 已知数列 是公比为4的等比数列,且满足a2, a4, a7成等比数列,求数列 的前n项和Tn.
变式训练
2.在数列{an}中,
,求数列{bn}的前n项的和.
变式训练
新课讲解
(1)一般情况下形如cn=an±bn ;
(2)数列{an}与{bn}是等差数列, 或等比数列, 或是其他已知求和方法的数列;
(3)求数列{cn}的前n项和,分别利用已知的求和方法;
如等差数列和等比数列前n项和公式求和即可.
五、分组求和法
典型例题
例5 已知数列{an}满足an =3an-1+2(n≥2),a1 =1,若bn =3an+2n-1,求数列{bn}的前n项和Tn.
典型例题
新课讲解
2.适用于通项中含有(-1)n的数列[摆动数列] ,形如an=(-1)nf(n),可采用两项合并求解.
3.涉及奇偶问题,则需要讨论n的奇偶性,分项数为奇数和偶数分别进行求和,最后综合.
六、并项求和法
1.求 一个数列的前n项和,可两两结合求解,则称之为并项求和.
典型例题
例6 求12-22+32-42+…+(-1)n-1n2.
七、分类讨论法
新课讲解
新课讲解
八、绝对值型求和
实际就是一个去绝对值的过程, 绝对值的临界值就是分类讨论的点.
已知数列{an}的前n项和为Sn, 求数列{|an|}的前n项和Tn.
思路:由an≥0, 得n≤n0(不妨设为n0整数)
当1≤n≤n0时, an≥0;而当n≥n0+1时, an≤0.
当1≤n≤n0时, Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn
当n≥n0+1时, Tn=|a1|+|a2|+…+|an0|+|an0+1|+…+|an|
=(a1+a2+…+an0)-(an0+1+…+an)
=Sn0-(Sn-Sn0)
=2Sn0-Sn
综上,
典型例题
例8 已知数列{an}的前n项和为Sn=14n-n2,求数列{|an|}的前n项和Tn.
巩固训练
1.求数列1,3+5,7+9+11,13+15+17+19,…的前n项和.
这些奇数组成等差数列,首项为1,公差为2,
故该数列的前n项和
巩固训练
20
巩固训练
解: (1)当x=±1时,Sn=4n.
综上可知,
(2)当x≠±1时,
巩固训练
巩固训练
4.求和:Sn=-1+3-5+7-…+(-1)n(2n-1).
解:当n为奇数时,
Sn=(-1+3)+(-5+7)+(-9+11)+…+[(-2n+5)+(2n-3)]+(-2n+1)
当n为偶数时,
∴Sn=(-1)n·n (n∈N*).
巩固训练
5.求和:Sn=x+2x2+3x3+…+nxn(x≠0).
当x≠1时,Sn=x + 2x2 + 3x3 + 4x4 +…(n-1)xn-1+ nxn,
xSn= x2 + 2x3 + 3x4 +… … +(n-1)xn+nxn+1,
∴(1-x)Sn=x + x2 + x3 + … … … … … + xn -nxn+1
巩固训练
巩固训练
7. 已知等差数列{an}中, 公差d=2, a2是a1和a4的等比中项.设 ,
求数列{bn}的前n项和Tn.
课堂小结
1.公式法
(2)四类特殊数列的前n项和
(1)等差、等比数列的前n项和公式;
求数列前n项和的方法
3.错位相减法
(1)形如cn=an·bn, 一个是等差数列,一个是等比数列;
(2)步骤:乘公比,错位减
(2)数列{an}与首末两端等“距离”的两项和相等,则用倒序相加法求和.
2.倒序相加法
(1)将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n个(a1+an);
4.裂项相消法
(1)通项公式为分式,可用待定系数法对通项公式拆项;
(2)记住常见的拆项公式
课堂小结
(1)适用于通项中含有(-1)n的数列[摆动数列] ;
6.并项求和法
(2)也可分奇数项和偶数项求和
求数列前n项和的方法
8.绝对值型求和
实际就是一个去绝对值的过程, 绝对值的临界值就是分类讨论的点.
5.分组求和法
(2)数列{an}与{bn}是已知求和方法的数列;
(1)一般情况下形如cn=an±bn ;
7.分奇偶讨论
本节课你有哪些收获?请做一下总结!
小结
