4.4 高中数学归纳法 课件(共21张PPT)-高中数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 4.4 高中数学归纳法 课件(共21张PPT)-高中数学人教A版(2019)选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 18:46:26 | ||
图片预览







文档简介
(共21张PPT)
4.4 数学归纳法
情景引入
我是一毛
我是二毛
我是三毛
我是谁?
我不是四毛!我是小明!
猜:
四毛!
不完全归纳:
从一类对象中的部分对象都具有某种性质推出这类对象全体都具有这种性质的归纳推理方法
探究新知
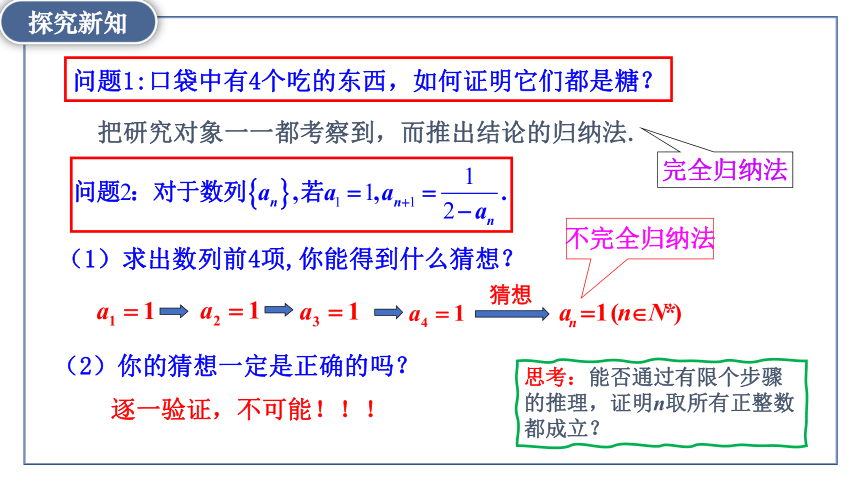
问题1:口袋中有4个吃的东西,如何证明它们都是糖?
把研究对象一一都考察到,而推出结论的归纳法.
完全归纳法
(1)求出数列前4项,你能得到什么猜想?
(2)你的猜想一定是正确的吗?
猜想
不完全归纳法
逐一验证,不可能!!!
思考:能否通过有限个步骤的推理,证明n取所有正整数都成立?
情景引入
我们先从多米诺骨牌游戏说起.码放骨牌时,要保证任意相邻的两块骨牌,若前一块骨牌倒下,则一定导致后块骨牌倒下.这样,只要推倒第1块骨牌,就可导致第2块骨牌倒下;而第2块骨牌倒下,就可导致第3块骨牌倒下;…….总之,不论有多少块骨牌,都能全部倒下.
探究新知
思考1:在这个游戏中,能使所有多米诺骨牌全部倒下的条件是什么?
使所有多米诺骨牌全部倒下的条件有两个:
(1)第一块骨牌倒下;
(2)任意相邻的两块骨牌,前一块倒下一定导致后一块倒下.
思考2:你认为条件(2)的作用是什么?如何用数学语言描述它?
条件(2)实际上是给出了一个递推关系.
数学语言:
第k块骨牌倒下
第k+1块骨牌倒下
结论:无论有多少块骨牌,只要保证条件(1)(2)出来,那么所有的骨牌都能倒下.
探究新知
探究:已知数列{}满足=1,计算,,,猜想其通项公式,并证明你的猜想.
解:由=1,计算可得=1,=1,=1.
由此=1.
证明:(1)当=1时=1显然成立.
(2)假设=k时结论成立,即=1.
当=k+1时
=1.
即当=k+1时结论也成立.
由(1) (2)可知,=1对任何成立.
新课讲解
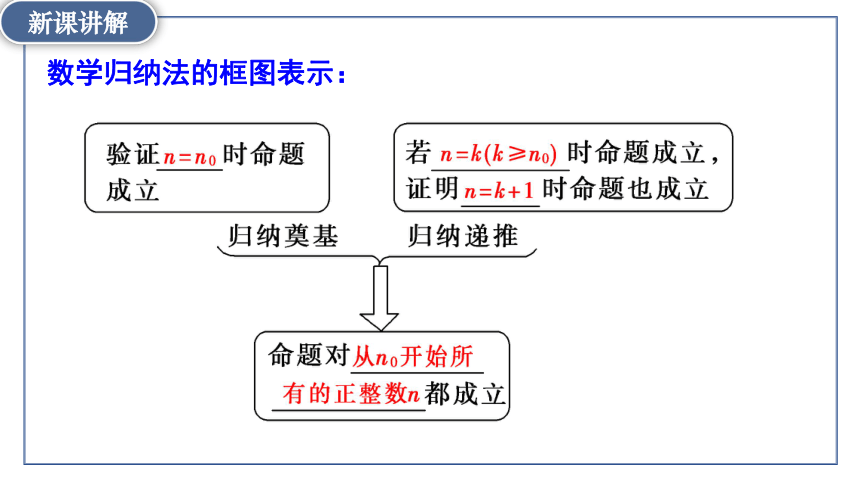
只要完成这两个步骤,就可以断定命题对从n0开始的所有正整数n都成立.
数学归纳法的定义
一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
(1)归纳奠基:证明当n=n0(n0∈N*)时命题成立;
(2)归纳递推:以“当n=k(k∈N*,k≥n0)时命题成立”为条件,推出“当__________时命题也成立”.
n=k+1
这种证明方法称为数学归纳法.
思考:数学归纳法的第一步n0的初始值是否一定为1
不一定.如证明n边形的内角和为(n-2)·180°,第一个值n0=3.
新课讲解
数学归纳法的框图表示:
小试牛刀
1.判断正误(正确的打“√”,错误的打“×”)
(1)用数学归纳法证题时可以只证明归纳递推即可. ( )
(2)数学归纳法证明3n≥n2(n≥3,n∈N*),第一步验证n=3. ( )
(3)设Sk=+++…+,则Sk+1=+++…+
. ( )
×
√
×
2.用数学归纳法证明1+a+a2+…+an+1=(a≠1,n∈N*),在验证n=1成立时,左边计算所得的项是( )
A.1 B.1+a
C.1+a+a2 D.1+a+a2+a3
C
典型例题
例1 用数学归纳法证明:如果{}是一个公差为d的等差数列,那么满足任何成立.
证明: (1)当=1时,左边=,右边=+0×=,命题成立.
(2)假设当= ()时, 等式成立, 即
那么
]
由(1)和(2)可知,任何都成立.
即当= +1时,等式也成立.
归纳假设
]
目 标
新课讲解
用数学归纳法证明一个与正整数有关命题的步骤:
使用前提
基础性
结 论
传递性
(1)证明当取第一个值n0(例如n0=1或2)时结论正确;
(2)假设当n=k(k∈N*,且k≥ n0 )时结论正确,证明当n=k+1时结论也正确.
据(1)和(2)可知命题对于从n0开始的所有正整数n都正确.
口诀:递推基础不可少,归纳假设要用到,结论写明莫忘掉.
典型例题
例2 用数学归纳法证明:.
证明: (1)当=1时, 等式左边= =1,
右边= = ,等式成立.
(2)假设当= ()时,等式成立,即=
由(1)和(2)可知,等式对任何都成立.
那么
即当= +1时,等式也成立.
目 标
典型例题
例3 已知数列{}满足=0,试猜想数列{}的通项公式,并用数学归纳法加以证明.
解: 由可得
由可得
同理可得
归纳上述结果,猜想
分析: 先将数列{}的递推关系化为,通过计算,,,的值,归纳共性并作出猜想,再应用数学归纳法证明猜想.
典型例题
证明: (2)当=1时,左边==0,右边==,猜想成立.
那么
(2)假设当= ()时,等式成立,即
由(1)和(2)可知,猜想对任何成立.
即当= +1时,猜想也成立.
例3 已知数列{}满足=0,试猜想数列{}的通项公式,并用数学归纳法加以证明.
目 标
归纳小结
“归纳—猜想—证明”的一般环节
典型例题
例4 设正实数,大于1的正整数,若数列前项和为,试比较与的大小,并用数学归纳法证明你的结论.
分析: 该问题中涉及两个字母和,是正实数,是大于1的正整数.
思路1: 是不求和,而直接通过取特殊值比较与的大小关系,并作出猜想,然后用数学归纳法证明得到的猜想;
思路2: 是先由等比数列的求和公式求出,再通过取特殊值比较与的大小关系后作出猜想,然后用数学归纳法证明得到的猜想.
典型例题
解法1: 由已知可得
当=2时,
由>0,可得>2;
当=3时,
++
由>0,可得>3;
由此,我们猜想,当>0, 且>1时,可得> .
例4 设正实数,大于1的正整数,若数列前项和为,试比较与的大小,并用数学归纳法证明你的结论.
典型例题
证明: (1)当=2时, 不等式显然成立.
>
(2)假设当= (且>1时,不等式成立,即>
那么+
由>0,可得
所以
即当= +1时,不等式也成立.
由(1)和(2)可知,不等式> 任意大于1的正整数都成立.
例4 设正实数,大于1的正整数,若数列前项和为,试比较与的大小,并用数学归纳法证明你的结论.
总结提升
(2)瞄准当n=k+1时的递推目标,有目的地放缩、分析直到凑出结论.
2.数学归纳法证明的第二步中要注意以下两点:
(1)先凑假设,作等价变换;
(3)证明n=k+1时结论也成立,要设法将待证式与归纳假设建立联系,并朝n=k+1证明目标的表达式变形.
1.用数学归纳法证明命题时,应关注以下三点:
(1)弄清n取第一个值n0时等式两端项的情况;
(2)弄清从n=k到n=k+1等式两端增加了哪些项,减少了哪些项;
总结提升:
课堂小结
用数学归纳法证明一个与正整数有关命题的步骤:
使用前提
基础性
结 论
传递性
(1)证明当取第一个值n0(例如n0=1或2)时结论正确;
(2)假设当n=k(k∈N*,且k≥ n0 )时结论正确,证明当n=k+1时结论也正确.
据(1)和(2)可知命题对于从n0开始的所有正整数n都正确.
口诀:递推基础不可少,归纳假设要用到,结论写明莫忘掉.
本节课你有哪些收获?请做一下总结!
小结
4.4 数学归纳法
情景引入
我是一毛
我是二毛
我是三毛
我是谁?
我不是四毛!我是小明!
猜:
四毛!
不完全归纳:
从一类对象中的部分对象都具有某种性质推出这类对象全体都具有这种性质的归纳推理方法
探究新知
问题1:口袋中有4个吃的东西,如何证明它们都是糖?
把研究对象一一都考察到,而推出结论的归纳法.
完全归纳法
(1)求出数列前4项,你能得到什么猜想?
(2)你的猜想一定是正确的吗?
猜想
不完全归纳法
逐一验证,不可能!!!
思考:能否通过有限个步骤的推理,证明n取所有正整数都成立?
情景引入
我们先从多米诺骨牌游戏说起.码放骨牌时,要保证任意相邻的两块骨牌,若前一块骨牌倒下,则一定导致后块骨牌倒下.这样,只要推倒第1块骨牌,就可导致第2块骨牌倒下;而第2块骨牌倒下,就可导致第3块骨牌倒下;…….总之,不论有多少块骨牌,都能全部倒下.
探究新知
思考1:在这个游戏中,能使所有多米诺骨牌全部倒下的条件是什么?
使所有多米诺骨牌全部倒下的条件有两个:
(1)第一块骨牌倒下;
(2)任意相邻的两块骨牌,前一块倒下一定导致后一块倒下.
思考2:你认为条件(2)的作用是什么?如何用数学语言描述它?
条件(2)实际上是给出了一个递推关系.
数学语言:
第k块骨牌倒下
第k+1块骨牌倒下
结论:无论有多少块骨牌,只要保证条件(1)(2)出来,那么所有的骨牌都能倒下.
探究新知
探究:已知数列{}满足=1,计算,,,猜想其通项公式,并证明你的猜想.
解:由=1,计算可得=1,=1,=1.
由此=1.
证明:(1)当=1时=1显然成立.
(2)假设=k时结论成立,即=1.
当=k+1时
=1.
即当=k+1时结论也成立.
由(1) (2)可知,=1对任何成立.
新课讲解
只要完成这两个步骤,就可以断定命题对从n0开始的所有正整数n都成立.
数学归纳法的定义
一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
(1)归纳奠基:证明当n=n0(n0∈N*)时命题成立;
(2)归纳递推:以“当n=k(k∈N*,k≥n0)时命题成立”为条件,推出“当__________时命题也成立”.
n=k+1
这种证明方法称为数学归纳法.
思考:数学归纳法的第一步n0的初始值是否一定为1
不一定.如证明n边形的内角和为(n-2)·180°,第一个值n0=3.
新课讲解
数学归纳法的框图表示:
小试牛刀
1.判断正误(正确的打“√”,错误的打“×”)
(1)用数学归纳法证题时可以只证明归纳递推即可. ( )
(2)数学归纳法证明3n≥n2(n≥3,n∈N*),第一步验证n=3. ( )
(3)设Sk=+++…+,则Sk+1=+++…+
. ( )
×
√
×
2.用数学归纳法证明1+a+a2+…+an+1=(a≠1,n∈N*),在验证n=1成立时,左边计算所得的项是( )
A.1 B.1+a
C.1+a+a2 D.1+a+a2+a3
C
典型例题
例1 用数学归纳法证明:如果{}是一个公差为d的等差数列,那么满足任何成立.
证明: (1)当=1时,左边=,右边=+0×=,命题成立.
(2)假设当= ()时, 等式成立, 即
那么
]
由(1)和(2)可知,任何都成立.
即当= +1时,等式也成立.
归纳假设
]
目 标
新课讲解
用数学归纳法证明一个与正整数有关命题的步骤:
使用前提
基础性
结 论
传递性
(1)证明当取第一个值n0(例如n0=1或2)时结论正确;
(2)假设当n=k(k∈N*,且k≥ n0 )时结论正确,证明当n=k+1时结论也正确.
据(1)和(2)可知命题对于从n0开始的所有正整数n都正确.
口诀:递推基础不可少,归纳假设要用到,结论写明莫忘掉.
典型例题
例2 用数学归纳法证明:.
证明: (1)当=1时, 等式左边= =1,
右边= = ,等式成立.
(2)假设当= ()时,等式成立,即=
由(1)和(2)可知,等式对任何都成立.
那么
即当= +1时,等式也成立.
目 标
典型例题
例3 已知数列{}满足=0,试猜想数列{}的通项公式,并用数学归纳法加以证明.
解: 由可得
由可得
同理可得
归纳上述结果,猜想
分析: 先将数列{}的递推关系化为,通过计算,,,的值,归纳共性并作出猜想,再应用数学归纳法证明猜想.
典型例题
证明: (2)当=1时,左边==0,右边==,猜想成立.
那么
(2)假设当= ()时,等式成立,即
由(1)和(2)可知,猜想对任何成立.
即当= +1时,猜想也成立.
例3 已知数列{}满足=0,试猜想数列{}的通项公式,并用数学归纳法加以证明.
目 标
归纳小结
“归纳—猜想—证明”的一般环节
典型例题
例4 设正实数,大于1的正整数,若数列前项和为,试比较与的大小,并用数学归纳法证明你的结论.
分析: 该问题中涉及两个字母和,是正实数,是大于1的正整数.
思路1: 是不求和,而直接通过取特殊值比较与的大小关系,并作出猜想,然后用数学归纳法证明得到的猜想;
思路2: 是先由等比数列的求和公式求出,再通过取特殊值比较与的大小关系后作出猜想,然后用数学归纳法证明得到的猜想.
典型例题
解法1: 由已知可得
当=2时,
由>0,可得>2;
当=3时,
++
由>0,可得>3;
由此,我们猜想,当>0, 且>1时,可得> .
例4 设正实数,大于1的正整数,若数列前项和为,试比较与的大小,并用数学归纳法证明你的结论.
典型例题
证明: (1)当=2时, 不等式显然成立.
>
(2)假设当= (且>1时,不等式成立,即>
那么+
由>0,可得
所以
即当= +1时,不等式也成立.
由(1)和(2)可知,不等式> 任意大于1的正整数都成立.
例4 设正实数,大于1的正整数,若数列前项和为,试比较与的大小,并用数学归纳法证明你的结论.
总结提升
(2)瞄准当n=k+1时的递推目标,有目的地放缩、分析直到凑出结论.
2.数学归纳法证明的第二步中要注意以下两点:
(1)先凑假设,作等价变换;
(3)证明n=k+1时结论也成立,要设法将待证式与归纳假设建立联系,并朝n=k+1证明目标的表达式变形.
1.用数学归纳法证明命题时,应关注以下三点:
(1)弄清n取第一个值n0时等式两端项的情况;
(2)弄清从n=k到n=k+1等式两端增加了哪些项,减少了哪些项;
总结提升:
课堂小结
用数学归纳法证明一个与正整数有关命题的步骤:
使用前提
基础性
结 论
传递性
(1)证明当取第一个值n0(例如n0=1或2)时结论正确;
(2)假设当n=k(k∈N*,且k≥ n0 )时结论正确,证明当n=k+1时结论也正确.
据(1)和(2)可知命题对于从n0开始的所有正整数n都正确.
口诀:递推基础不可少,归纳假设要用到,结论写明莫忘掉.
本节课你有哪些收获?请做一下总结!
小结
