5.3.2函数的极值与最大(小)值(共66张PPT) -高中数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 5.3.2函数的极值与最大(小)值(共66张PPT) -高中数学人教A版(2019)选择性必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 08:58:31 | ||
图片预览






文档简介
(共65张PPT)
5.3.2 函数的极值与最大(小)值
第1课时 函数的极值
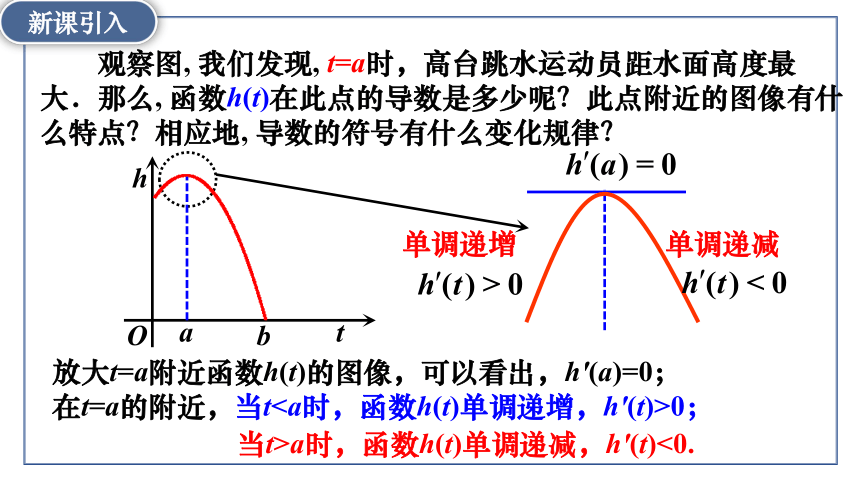
观察图, 我们发现, t=a时,高台跳水运动员距水面高度最大.那么, 函数h(t)在此点的导数是多少呢?此点附近的图像有什么特点?相应地, 导数的符号有什么变化规律?
O
t
a
b
h
单调递增
单调递减
放大t=a附近函数h(t)的图像,可以看出,h′(a)=0;
在t=a的附近,当t0;
当t>a时,函数h(t)单调递减,h′(t)<0.
新课引入
新课讲解
可以看出,;在t=a的附近,
当t当t>a时,函数 h(t)单调递减,.
在 t=a 附近,函数值先增后减.
这样当 t 在 a 的附近从小到大经过a时,先正后负,且连续变化,于是有.
对于一般的函数y=f(x),是否具有同样的性质?
新课讲解
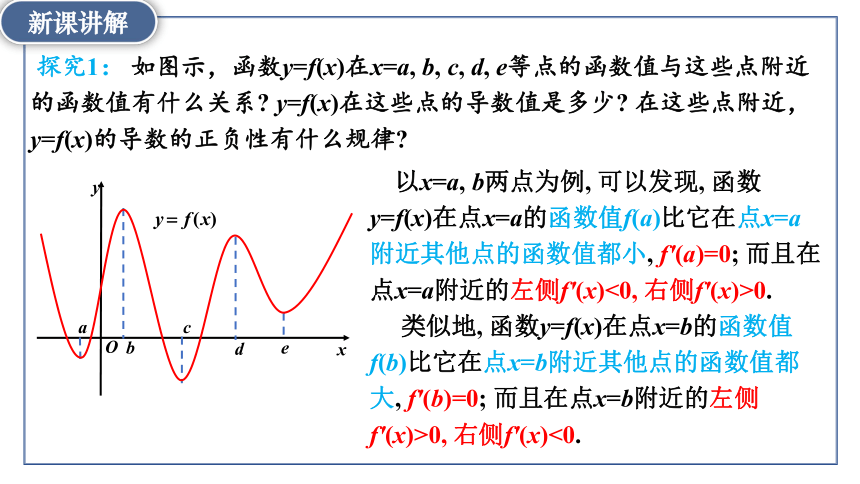
探究1: 如图示,函数y=f(x)在x=a, b, c, d, e等点的函数值与这些点附近的函数值有什么关系 y=f(x)在这些点的导数值是多少 在这些点附近, y=f(x)的导数的正负性有什么规律
以x=a, b两点为例, 可以发现, 函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小, f′(a)=0; 而且在点x=a附近的左侧f′(x)<0, 右侧f′(x)>0.
类似地, 函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大, f'(b)=0; 而且在点x=b附近的左侧f'(x)>0, 右侧f'(x)<0.
x
y
O
a
b
c
d
e
新课讲解
我们把a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值;
b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.
极小值点、极大值点统称为极值点,极小值和极大值统称为极值.
极值反映了函数在某一点附近的大小情况,刻画了函数的局部性质.
x
y
O
a
b
c
d
e
巩固训练
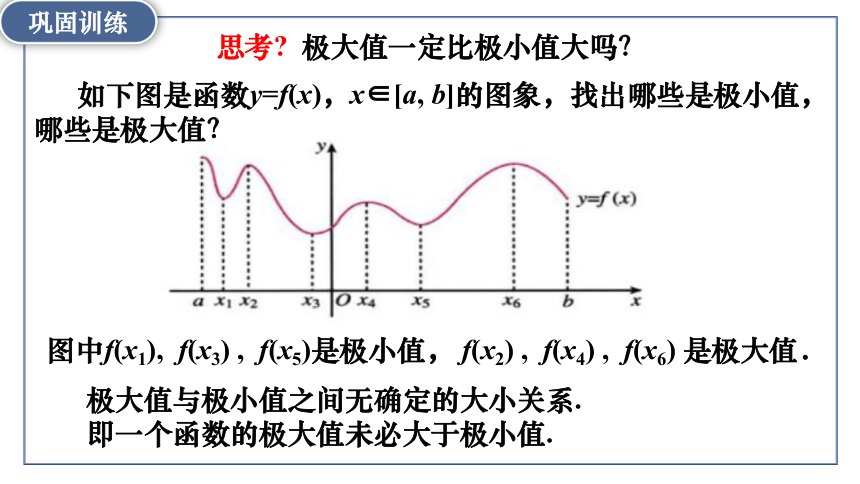
如下图是函数y=f(x),x∈[a, b]的图象,找出哪些是极小值,哪些是极大值?
思考 极大值一定比极小值大吗?
图中f(x1), f(x3) , f(x5)是极小值, f(x2) , f(x4) , f(x6) 是极大值.
极大值与极小值之间无确定的大小关系.
即一个函数的极大值未必大于极小值.
典型例题
例1
解:
x (-∞, -2) -2 (-2, 2) 2 (2, +∞)
f′(x)
f(x)
x
y
O
-2
2
新课讲解
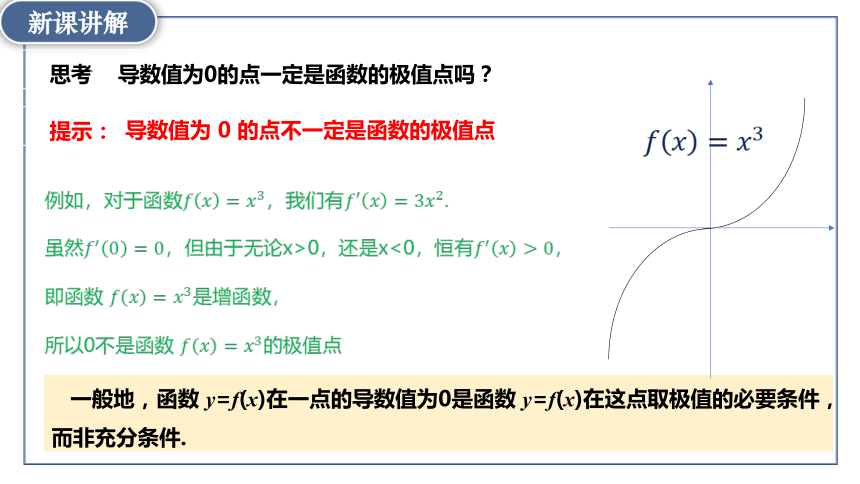
思考
导数值为0的点一定是函数的极值点吗?
提示:
导数值为 0 的点不一定是函数的极值点
例如,对于函数,我们有.
虽然,但由于无论x>0,还是x<0,恒有,
即函数 是增函数,
所以0不是函数 的极值点
一般地,函数 y=f(x)在一点的导数值为0是函数 y=f(x)在这点取极值的必要条件,而非充分条件.
概念辨析
(3) 极大值与极小值没有必然关系,极大值可能比极小值还小.
注意:
(1) 极值是某一点附近的小区间而言的,是函数的局部性质,不是整体的最值;
(2) 函数的极值不一定唯一,在整个定义区间内可能有多个极大值和极小值;
即f ′(x0)=0是函数f(x)在x0处取得极值的必要条件.
(4) 对于可导函数,若x0是极值点,则 f '(x0)=0;
反之,若f '(x0)=0,则x0不一定是极值点.
归纳总结
O
a
x0
b
x
y
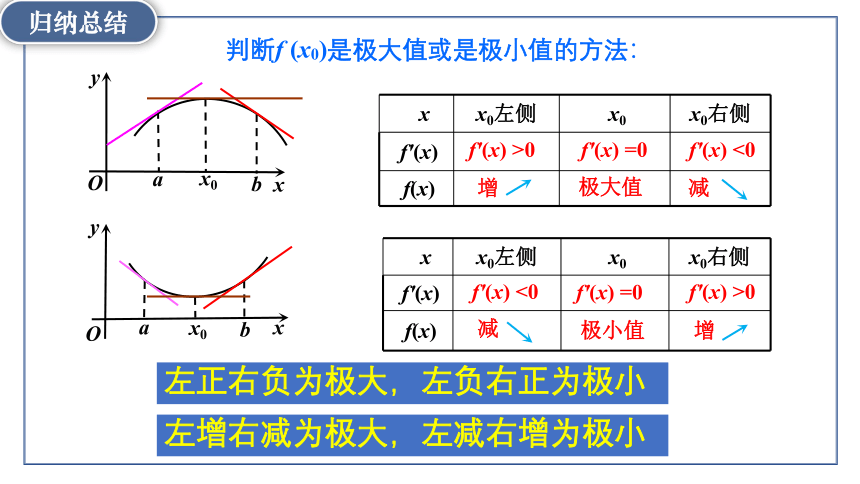
x x0左侧 x0 x0右侧
f′(x)
f(x)
O
a
x0
b
x
y
x x0左侧 x0 x0右侧
f′(x)
f(x)
增
f′(x) >0
f′(x) =0
f′(x) <0
极大值
减
f′(x) <0
f′(x) =0
增
减
极小值
f′(x) >0
判断f (x0)是极大值或是极小值的方法:
左正右负为极大,左负右正为极小
左增右减为极大,左减右增为极小
小结
求可导函数f(x)极值的步骤:
(2) 求导数f ′(x);
(3) 求方程f ′(x)=0的根;
(4) 把定义域划分为部分区间,并列成表格:
检查f ′(x)在方程根左右的符号:
如果左正右负(左增右减),
那么f(x)在这个根处取得极大值;
如果左负右正(左减右增),
那么f(x)在这个根处取得极小值;
(1) 确定函数的定义域;
新课讲解
解:
x
f′(x)
f(x)
新课讲解
解:
x (-∞, -3) -3 (-3, 3) 3 (3, +∞)
f′(x)
f(x)
新课讲解
解:
x (-∞, -2) -2 (-2, 2) 2 (2, +∞)
f′(x)
f(x)
新课讲解
解:
x (-∞, -1) -1 (-1, 1) 1 (1, +∞)
f′(x)
f(x)
新课讲解
D
新课讲解
D
新课讲解
课堂小结
函数的极值与导数的关系
(1)函数的极小值与极小值点
若函数f(x)在点x=a处的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0,而且在点x=a附近的左侧f′(x)<0,右侧f′(x)>0,则点a叫做函数的极小值点,f(a)叫做函数的极小值.
(2)函数的极大值与极大值点
若函数f(x)在点x=b处的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0,而且在点x=b附近的左侧f′(x)>0,右侧f′(x)<0,则点b叫做函数的极大值点,f(b)叫做函数的极大值.
本节课你有哪些收获?请做一下总结!
小结
5.3.2 函数的极值与最大(小)值
第2课时 函数的最大(小)值
复习回顾
如果在 x0 附近的左侧f '(x)>0, 右侧f '(x)<0 ,那么 f (x0)为极大值;
解方程 f '(x) = 0. 当 f '(x0) = 0 时:
如果在 x0 附近的左侧f '(x)<0, 右侧f '(x)>0 ,那么 f (x0)为极小值.
1.求函数 y=f(x)的极值的一般方法:
2.函数最大值和最小值的概念:
一般地,设函数y=f(x)的定义域为I,如果存在实数M 满足:
(1)对于任意的x∈I,都有f(x)≤M ; (2)存在 x0∈I,使得f(x0) = M
那么,称M 是函数y=f(x)的最大值.
一般地,设函数y=f(x)的定义域为I ,如果存在实数M 满足:
(2)对于任意的x∈I ,都有f(x)≥M ; (2)存在 x0∈I,使得f(x0) = M
那么,称M 是函数y=f(x)的最小值 .
新课讲解
我们知道,极值反映的是函数在某一点附近的局部性质,而不是函数在整个定义域内的性质.
也就是说,如果x0是函数y=f(x)的极大(小)值点,那么在x= x0附近找不到比f(x0)更大(小)的值.
但是,在解决实际问题或研究函数的性质时,我们往往更关心函数在某个区间上,哪个值最大,哪个值最小.
如果x0是某个区间上函数y=f(x)的最大(小)值点,那么f(x0)不小(大)于函数y=f(x)在此区间上的所有函数值.
新课讲解
思考1 下图是函数y=f(x), x∈[a, b]的图象,你能找出它的极小(大)值吗 你能进一步找出函数在区间[a, b]上的最小(大)值吗?
x
y
O
a
b
x1
x2
x3
x4
x5
x6
新课讲解
思考2 在图(1)、图(2)中,观察[a, b]上的函数y=f(x)和y=g(x)的图象,它们在[a, b]上有最大值、最小值吗 如果有,最大值和最小值分别是什么
x
y
O
a
b
(1)
(2)
x
y
O
a
b
x1
x2
x3
x4
x5
一般地,如果在区间[a, b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.由上述例子可知,只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值与最小值.
新课讲解
例1
解:
x 0 (0, 2) 2 (2, 3) 3
f′(x)
f(x)
x
y
O
4
2
3
题型一:利用导数求最值
方法归纳
求f(x)在[a,b]上的最大值与最小值的步骤如下:
(2) 将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(1) f(x)在(a,b)内导函数为零的点,并计算出其函数值;
巩固训练
解:
巩固训练
证明:
题型二:利用最值证明不等式
典型例题
题型二:利用最值证明不等式
典型例题
总结升华
重要函数不等式链
典型例题
题型三:利用最值证明恒成立问题
典型例题
题型三:利用最值证明恒成立问题
巩固训练
A
巩固训练
新课讲解
4.求下列函数在给定区间上的最大值与最小值:
解: (1)因为
x
f '(x) 0
f (x)
–
+
单调递减
单调递增
又因为f(0)=-2,f(2)=20
所以,当x=2时,函数f(x)在[0,3]上取得最大值20,
当x= 时,函数f(x)在[0,3]上取得最小值 .
令 解得 .
新课讲解
4.求下列函数在给定区间上的最大值与最小值:
x 2 ( 2, 3)
f '(x) 0
f (x)
–
+
单调递减
单调递增
解: (2)因为
又因为
所以,当x=2时,函数f(x)在 上取得最大值20,
当x= 时,函数f(x)在 上取得最小值 .
令 解得 .
课堂小结
2.求f(x)在[a,b]上的最大值与最小值的步骤:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(2)将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
1.求最大(小)值的方法
只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值.
3.解决优化问题的基本思路:
优化问题→用函数表示的数学问题→用导数解决数学问题→优化问题的答案→优化问题
5.3.2 函数的极值与最大(小)值
第3课时 含参数的函数的最大(小)值
解决恒成立或有解问题有哪些常见结论?
新课引入
下列是恒成立问题的一些常见结论:
(1)不等式f(x)≥0在定义域内恒成立,等价于f(x)min≥0;
(2)不等式f(x)≤0在定义域内恒成立,等价于f(x)max≤0;
(3)不等式f(x)>g(x),x∈(a,b)恒成立,等价于F(x)=f(x)-g(x)>0,x∈(a,b)恒成立.
下列是有解问题的一些常见结论:
(1)不等式f(x)≥0在定义域内有解,等价于f(x)max≥0;
(2)不等式f(x)≤0在定义域内有解,等价于f(x)min≤0;
(3)不等式f(x)>g(x),x∈(a,b)有解,等价于F(x)=f(x)-g(x)>0,x∈(a,b)有解.
典型例题
题型一:含参最值问题
典型例题
题型一:含参最值问题
典型例题
题型二:恒成立问题求参数取值范围
典型例题
题型二:恒成立问题求参数取值范围
典型例题
题型三:双变量恒成立问题求参数
典型例题
题型四:存在性问题求参数
直接改为:单调递增
5.3.2 函数的极值与最大(小)值
第4课时 图象与零点问题
新课讲解
1.利用导数解决与函数相关的问题:
例7
解:
新课讲解
例7
解:
x
y
O
1
-1
-2
新课讲解
例7
解:
x
y
O
1
-1
-2
巩固训练
1.
x
y
O
-1
变式:
巩固训练
1.
变式:
1
e
e
新课讲解
由例7可见,函数f(x)的图象直观地反映了函数f(x)的性质. 通常,可以按如下步骤画出函数f(x)的大致图象:
(1) 求出函数f(x)的定义域;
(2) 求导数f′(x)及函数f′(x)的零点;
(3) 用f′(x)的零点将f(x)的定义域划分为若干个区间,列表给出f′(x)在各区间上的正负,并得出f(x)的单调性与极值;
(4) 确定f(x)的图象所经过的一些特殊点,以及图象的变化趋势;
(5) 画出f(x)的大致图象.
零点问题
新课讲解
2.导数在解决实际问题中的应用
问题 饮料瓶大小对饮料公司利润的影响
(1) 你是否注意过,市场上等量的小包装的物品一般比大包装的要贵些 你想从数学上知道它的道理吗
(2) 是不是饮料瓶越大,饮料公司的利润越大
例8 某制造商制造并出售球形瓶装的某种饮料. 瓶子的制造成本是0.8πr2分,其中r(单位: cm)是瓶子的半径. 已知每出售1 mL的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为6 cm.
(1) 瓶子半径多大时,能使每瓶饮料的利润最大
(2) 瓶子半径多大时,每瓶饮料的利润最小
新课讲解
例8 某制造商制造并出售球形瓶装的某种饮料. 瓶子的制造成本是0.8πr2分,其中r(单位: cm)是瓶子的半径. 已知每出售1 mL的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为6 cm.
(1) 瓶子半径多大时,能使每瓶饮料的利润最大
(2) 瓶子半径多大时,每瓶饮料的利润最小
解:
巩固训练
证明:
x
y
O
1
π
巩固训练
解:
2.如图,用铁丝围成一个上面是半圆,下面是矩形的图形,其面积为a m2.为使所用材料最省,圆的直径应为多少 .
新课讲解
3.已知f(x)=ax-ln x,a∈R.
(1)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程;
(2)是否存在实数a,使f(x)在区间(0,e]上的最小值是3,若存在,求出a的值;若不存在,说明理由.
新课讲解
①当a≤0时,f(x)在(0,e]上单调递减,
综上,存在实数a=e2,使得当x∈(0,e]时,f(x)有最小值3.
新课讲解
新课讲解
新课讲解
课堂小结
求f(x)在[a,b]上的最大值与最小值的步骤如下:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(2)将f(x)的各导数值为零的点的函数值与f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
5.3.2 函数的极值与最大(小)值
第1课时 函数的极值
观察图, 我们发现, t=a时,高台跳水运动员距水面高度最大.那么, 函数h(t)在此点的导数是多少呢?此点附近的图像有什么特点?相应地, 导数的符号有什么变化规律?
O
t
a
b
h
单调递增
单调递减
放大t=a附近函数h(t)的图像,可以看出,h′(a)=0;
在t=a的附近,当t
当t>a时,函数h(t)单调递减,h′(t)<0.
新课引入
新课讲解
可以看出,;在t=a的附近,
当t
在 t=a 附近,函数值先增后减.
这样当 t 在 a 的附近从小到大经过a时,先正后负,且连续变化,于是有.
对于一般的函数y=f(x),是否具有同样的性质?
新课讲解
探究1: 如图示,函数y=f(x)在x=a, b, c, d, e等点的函数值与这些点附近的函数值有什么关系 y=f(x)在这些点的导数值是多少 在这些点附近, y=f(x)的导数的正负性有什么规律
以x=a, b两点为例, 可以发现, 函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小, f′(a)=0; 而且在点x=a附近的左侧f′(x)<0, 右侧f′(x)>0.
类似地, 函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大, f'(b)=0; 而且在点x=b附近的左侧f'(x)>0, 右侧f'(x)<0.
x
y
O
a
b
c
d
e
新课讲解
我们把a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值;
b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.
极小值点、极大值点统称为极值点,极小值和极大值统称为极值.
极值反映了函数在某一点附近的大小情况,刻画了函数的局部性质.
x
y
O
a
b
c
d
e
巩固训练
如下图是函数y=f(x),x∈[a, b]的图象,找出哪些是极小值,哪些是极大值?
思考 极大值一定比极小值大吗?
图中f(x1), f(x3) , f(x5)是极小值, f(x2) , f(x4) , f(x6) 是极大值.
极大值与极小值之间无确定的大小关系.
即一个函数的极大值未必大于极小值.
典型例题
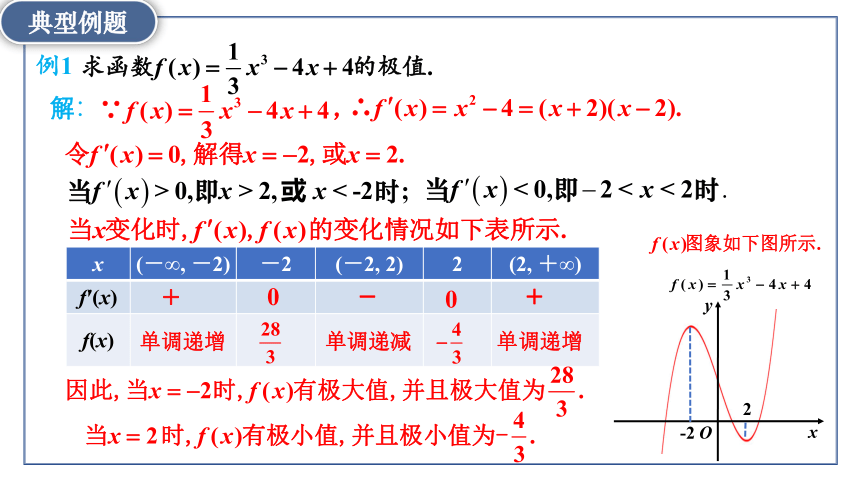
例1
解:
x (-∞, -2) -2 (-2, 2) 2 (2, +∞)
f′(x)
f(x)
x
y
O
-2
2
新课讲解
思考
导数值为0的点一定是函数的极值点吗?
提示:
导数值为 0 的点不一定是函数的极值点
例如,对于函数,我们有.
虽然,但由于无论x>0,还是x<0,恒有,
即函数 是增函数,
所以0不是函数 的极值点
一般地,函数 y=f(x)在一点的导数值为0是函数 y=f(x)在这点取极值的必要条件,而非充分条件.
概念辨析
(3) 极大值与极小值没有必然关系,极大值可能比极小值还小.
注意:
(1) 极值是某一点附近的小区间而言的,是函数的局部性质,不是整体的最值;
(2) 函数的极值不一定唯一,在整个定义区间内可能有多个极大值和极小值;
即f ′(x0)=0是函数f(x)在x0处取得极值的必要条件.
(4) 对于可导函数,若x0是极值点,则 f '(x0)=0;
反之,若f '(x0)=0,则x0不一定是极值点.
归纳总结
O
a
x0
b
x
y
x x0左侧 x0 x0右侧
f′(x)
f(x)
O
a
x0
b
x
y
x x0左侧 x0 x0右侧
f′(x)
f(x)
增
f′(x) >0
f′(x) =0
f′(x) <0
极大值
减
f′(x) <0
f′(x) =0
增
减
极小值
f′(x) >0
判断f (x0)是极大值或是极小值的方法:
左正右负为极大,左负右正为极小
左增右减为极大,左减右增为极小
小结
求可导函数f(x)极值的步骤:
(2) 求导数f ′(x);
(3) 求方程f ′(x)=0的根;
(4) 把定义域划分为部分区间,并列成表格:
检查f ′(x)在方程根左右的符号:
如果左正右负(左增右减),
那么f(x)在这个根处取得极大值;
如果左负右正(左减右增),
那么f(x)在这个根处取得极小值;
(1) 确定函数的定义域;
新课讲解
解:
x
f′(x)
f(x)
新课讲解
解:
x (-∞, -3) -3 (-3, 3) 3 (3, +∞)
f′(x)
f(x)
新课讲解
解:
x (-∞, -2) -2 (-2, 2) 2 (2, +∞)
f′(x)
f(x)
新课讲解
解:
x (-∞, -1) -1 (-1, 1) 1 (1, +∞)
f′(x)
f(x)
新课讲解
D
新课讲解
D
新课讲解
课堂小结
函数的极值与导数的关系
(1)函数的极小值与极小值点
若函数f(x)在点x=a处的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0,而且在点x=a附近的左侧f′(x)<0,右侧f′(x)>0,则点a叫做函数的极小值点,f(a)叫做函数的极小值.
(2)函数的极大值与极大值点
若函数f(x)在点x=b处的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0,而且在点x=b附近的左侧f′(x)>0,右侧f′(x)<0,则点b叫做函数的极大值点,f(b)叫做函数的极大值.
本节课你有哪些收获?请做一下总结!
小结
5.3.2 函数的极值与最大(小)值
第2课时 函数的最大(小)值
复习回顾
如果在 x0 附近的左侧f '(x)>0, 右侧f '(x)<0 ,那么 f (x0)为极大值;
解方程 f '(x) = 0. 当 f '(x0) = 0 时:
如果在 x0 附近的左侧f '(x)<0, 右侧f '(x)>0 ,那么 f (x0)为极小值.
1.求函数 y=f(x)的极值的一般方法:
2.函数最大值和最小值的概念:
一般地,设函数y=f(x)的定义域为I,如果存在实数M 满足:
(1)对于任意的x∈I,都有f(x)≤M ; (2)存在 x0∈I,使得f(x0) = M
那么,称M 是函数y=f(x)的最大值.
一般地,设函数y=f(x)的定义域为I ,如果存在实数M 满足:
(2)对于任意的x∈I ,都有f(x)≥M ; (2)存在 x0∈I,使得f(x0) = M
那么,称M 是函数y=f(x)的最小值 .
新课讲解
我们知道,极值反映的是函数在某一点附近的局部性质,而不是函数在整个定义域内的性质.
也就是说,如果x0是函数y=f(x)的极大(小)值点,那么在x= x0附近找不到比f(x0)更大(小)的值.
但是,在解决实际问题或研究函数的性质时,我们往往更关心函数在某个区间上,哪个值最大,哪个值最小.
如果x0是某个区间上函数y=f(x)的最大(小)值点,那么f(x0)不小(大)于函数y=f(x)在此区间上的所有函数值.
新课讲解
思考1 下图是函数y=f(x), x∈[a, b]的图象,你能找出它的极小(大)值吗 你能进一步找出函数在区间[a, b]上的最小(大)值吗?
x
y
O
a
b
x1
x2
x3
x4
x5
x6
新课讲解
思考2 在图(1)、图(2)中,观察[a, b]上的函数y=f(x)和y=g(x)的图象,它们在[a, b]上有最大值、最小值吗 如果有,最大值和最小值分别是什么
x
y
O
a
b
(1)
(2)
x
y
O
a
b
x1
x2
x3
x4
x5
一般地,如果在区间[a, b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.由上述例子可知,只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值与最小值.
新课讲解
例1
解:
x 0 (0, 2) 2 (2, 3) 3
f′(x)
f(x)
x
y
O
4
2
3
题型一:利用导数求最值
方法归纳
求f(x)在[a,b]上的最大值与最小值的步骤如下:
(2) 将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(1) f(x)在(a,b)内导函数为零的点,并计算出其函数值;
巩固训练
解:
巩固训练
证明:
题型二:利用最值证明不等式
典型例题
题型二:利用最值证明不等式
典型例题
总结升华
重要函数不等式链
典型例题
题型三:利用最值证明恒成立问题
典型例题
题型三:利用最值证明恒成立问题
巩固训练
A
巩固训练
新课讲解
4.求下列函数在给定区间上的最大值与最小值:
解: (1)因为
x
f '(x) 0
f (x)
–
+
单调递减
单调递增
又因为f(0)=-2,f(2)=20
所以,当x=2时,函数f(x)在[0,3]上取得最大值20,
当x= 时,函数f(x)在[0,3]上取得最小值 .
令 解得 .
新课讲解
4.求下列函数在给定区间上的最大值与最小值:
x 2 ( 2, 3)
f '(x) 0
f (x)
–
+
单调递减
单调递增
解: (2)因为
又因为
所以,当x=2时,函数f(x)在 上取得最大值20,
当x= 时,函数f(x)在 上取得最小值 .
令 解得 .
课堂小结
2.求f(x)在[a,b]上的最大值与最小值的步骤:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(2)将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
1.求最大(小)值的方法
只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值.
3.解决优化问题的基本思路:
优化问题→用函数表示的数学问题→用导数解决数学问题→优化问题的答案→优化问题
5.3.2 函数的极值与最大(小)值
第3课时 含参数的函数的最大(小)值
解决恒成立或有解问题有哪些常见结论?
新课引入
下列是恒成立问题的一些常见结论:
(1)不等式f(x)≥0在定义域内恒成立,等价于f(x)min≥0;
(2)不等式f(x)≤0在定义域内恒成立,等价于f(x)max≤0;
(3)不等式f(x)>g(x),x∈(a,b)恒成立,等价于F(x)=f(x)-g(x)>0,x∈(a,b)恒成立.
下列是有解问题的一些常见结论:
(1)不等式f(x)≥0在定义域内有解,等价于f(x)max≥0;
(2)不等式f(x)≤0在定义域内有解,等价于f(x)min≤0;
(3)不等式f(x)>g(x),x∈(a,b)有解,等价于F(x)=f(x)-g(x)>0,x∈(a,b)有解.
典型例题
题型一:含参最值问题
典型例题
题型一:含参最值问题
典型例题
题型二:恒成立问题求参数取值范围
典型例题
题型二:恒成立问题求参数取值范围
典型例题
题型三:双变量恒成立问题求参数
典型例题
题型四:存在性问题求参数
直接改为:单调递增
5.3.2 函数的极值与最大(小)值
第4课时 图象与零点问题
新课讲解
1.利用导数解决与函数相关的问题:
例7
解:
新课讲解
例7
解:
x
y
O
1
-1
-2
新课讲解
例7
解:
x
y
O
1
-1
-2
巩固训练
1.
x
y
O
-1
变式:
巩固训练
1.
变式:
1
e
e
新课讲解
由例7可见,函数f(x)的图象直观地反映了函数f(x)的性质. 通常,可以按如下步骤画出函数f(x)的大致图象:
(1) 求出函数f(x)的定义域;
(2) 求导数f′(x)及函数f′(x)的零点;
(3) 用f′(x)的零点将f(x)的定义域划分为若干个区间,列表给出f′(x)在各区间上的正负,并得出f(x)的单调性与极值;
(4) 确定f(x)的图象所经过的一些特殊点,以及图象的变化趋势;
(5) 画出f(x)的大致图象.
零点问题
新课讲解
2.导数在解决实际问题中的应用
问题 饮料瓶大小对饮料公司利润的影响
(1) 你是否注意过,市场上等量的小包装的物品一般比大包装的要贵些 你想从数学上知道它的道理吗
(2) 是不是饮料瓶越大,饮料公司的利润越大
例8 某制造商制造并出售球形瓶装的某种饮料. 瓶子的制造成本是0.8πr2分,其中r(单位: cm)是瓶子的半径. 已知每出售1 mL的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为6 cm.
(1) 瓶子半径多大时,能使每瓶饮料的利润最大
(2) 瓶子半径多大时,每瓶饮料的利润最小
新课讲解
例8 某制造商制造并出售球形瓶装的某种饮料. 瓶子的制造成本是0.8πr2分,其中r(单位: cm)是瓶子的半径. 已知每出售1 mL的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为6 cm.
(1) 瓶子半径多大时,能使每瓶饮料的利润最大
(2) 瓶子半径多大时,每瓶饮料的利润最小
解:
巩固训练
证明:
x
y
O
1
π
巩固训练
解:
2.如图,用铁丝围成一个上面是半圆,下面是矩形的图形,其面积为a m2.为使所用材料最省,圆的直径应为多少 .
新课讲解
3.已知f(x)=ax-ln x,a∈R.
(1)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程;
(2)是否存在实数a,使f(x)在区间(0,e]上的最小值是3,若存在,求出a的值;若不存在,说明理由.
新课讲解
①当a≤0时,f(x)在(0,e]上单调递减,
综上,存在实数a=e2,使得当x∈(0,e]时,f(x)有最小值3.
新课讲解
新课讲解
新课讲解
课堂小结
求f(x)在[a,b]上的最大值与最小值的步骤如下:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(2)将f(x)的各导数值为零的点的函数值与f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
