勾股定理逆定理
图片预览








文档简介
课件25张PPT。 在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
执教者:温中实验学校 肖 亮18.2勾股定理逆定理知识回顾1:什么是勾股定理?C=5b=6C=10猜猜看:
分别以上述a、b 、c为边的三角形的形状 会是什么样的呢?勾股定理的逆定理执教者:温中实验学校 肖 亮准备活动:我们共同来画一个边长为2㎝,4㎝,5㎝的三角形.探究新知: 1.画图:画出边长分别是下列各组数的三角形(单位:厘米)
A:4、5、6 ;B:3、4、5;C:3、4、6;D:6、8、102.测量:用你的量角器分别测量一下上述各三角形的最大角的度数,并记录如下:
A:_______ B:_______ C:______ D:_______
8209009001200 3.判断:请判断一下上述你所画的三角形的形状.
A:______ B:_______ C:______ D:______直角三角形钝角三角形锐角三角形直角三角形 4.找规律:根据上述每个三角形所给的各组边长请你找出最长边 的平方与其他两边的平方和之间的关系。
A:______ B:_______ C:______ D:______
5.猜想:让我们猜想一下,一个三角形各边长数量应满足怎样的关系时,这个三角形才可能是直角三角形呢?
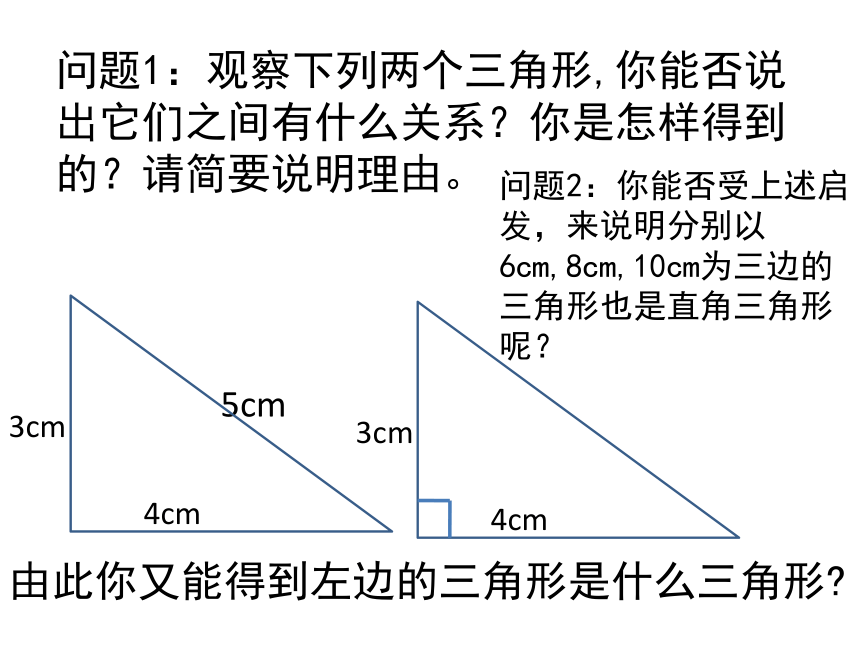
你的猜想是: 。两条较短边的平方和等于最长边的平方猜想结论:问题1:观察下列两个三角形,你能否说出它们之间有什么关系?你是怎样得到的?请简要说明理由。问题2:你能否受上述启发,来说明分别以6cm,8cm,10cm为三边的三角形也是直角三角形呢?由此你又能得到左边的三角形是什么三角形? 如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。证明猜想∵ ∠ C’=900∴ A’B’2= a2+b2∵ a2+b2=c2∴ A’B’ 2=c2∴ A’B’ =c∵ 边长取正值∴ △ ABC ≌△ A’B’C’(SSS)∴ ∠ C= ∠ C’(全等三角形对应角相等)∴ ∠C= 900已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2求证:△ ABC是直角三角形证明:画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=b在△ ABC和△ A’B’C’中∴ △ ABC是直角三角形(直角三角形的定义)一个三角形中两条较短边的平方和等于最长边的平方最长边解:∵152+82=225+64=289而 172=289∴ 152+82=172∴这个三角形是直角三角形∵72+82=113而 102=100∴这个三角形不是
直角三角形 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900勾股定理的逆命题勾股定理互逆命题题设结论互 换互逆命题:题设与结论正好相反的两个命题叫做互逆命题如果把其中一个叫做原命题,那么另一个叫做它的逆命题概念讲解(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的绝对值相等.
(3)对顶角相等.
(4)若ab=0,则a=0.说出下列命题的逆命题.并判断它们的逆命题是否成立。逆命题: 内错角相等,两条直线平行. 逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 逆命题:相等的角是对顶角. 逆命题:若a=0,则ab=0思考:原命题与逆命题的正确性是否一致?成立不成立不成立成立原命题成立时, 逆命题有时成立, 有时不成立成立成立成立不成立定理与逆定理我们已经学习了一些互逆的定理,如:
两直线平行,内错角相等;内错角相等,两直线平行.如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.勾股定理的逆命题勾股定理互逆命题逆定理定理2.指出下列命题中的互逆命题:
(1)直角都相等
(2)等腰三角形两底角相等
(3)如果a+b>0, 那么a>0,b>0
1.判断
(1)每一个命题都有逆命题( )
(2)如果原命题是真命题,那么它的逆命题也 一定是真命题( )
(3)原命题是假命题,但它的逆命题可能是真
命题( )
练一练√╳√相等的角是直角有两个角相等的三角形是等腰三角形如果a+b>0, 那么a>0,b>0
满足 的三个 ,称为勾股数。正整数你能写出常用的勾股数吗?3,4,5; 5,12,13;
6,8,10; 7,24,25;
9,12,15; 8,15,17 ;挑战自我
知识拓展BA、锐角三角形 B、直角三角形C、钝角三角形 D、等边三角形
已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
S四边形ABCD=36本节课我们学习了…1、勾股定理的逆定理2、什么叫做互逆命题、原命题与逆命题、
互逆定理
4、本节课用到了什么数学思想方法?3、勾股定理逆定理的简单应用再 见感谢各位光临指导!
——毕达哥拉斯
执教者:温中实验学校 肖 亮18.2勾股定理逆定理知识回顾1:什么是勾股定理?C=5b=6C=10猜猜看:
分别以上述a、b 、c为边的三角形的形状 会是什么样的呢?勾股定理的逆定理执教者:温中实验学校 肖 亮准备活动:我们共同来画一个边长为2㎝,4㎝,5㎝的三角形.探究新知: 1.画图:画出边长分别是下列各组数的三角形(单位:厘米)
A:4、5、6 ;B:3、4、5;C:3、4、6;D:6、8、102.测量:用你的量角器分别测量一下上述各三角形的最大角的度数,并记录如下:
A:_______ B:_______ C:______ D:_______
8209009001200 3.判断:请判断一下上述你所画的三角形的形状.
A:______ B:_______ C:______ D:______直角三角形钝角三角形锐角三角形直角三角形 4.找规律:根据上述每个三角形所给的各组边长请你找出最长边 的平方与其他两边的平方和之间的关系。
A:______ B:_______ C:______ D:______
5.猜想:让我们猜想一下,一个三角形各边长数量应满足怎样的关系时,这个三角形才可能是直角三角形呢?
你的猜想是: 。两条较短边的平方和等于最长边的平方猜想结论:问题1:观察下列两个三角形,你能否说出它们之间有什么关系?你是怎样得到的?请简要说明理由。问题2:你能否受上述启发,来说明分别以6cm,8cm,10cm为三边的三角形也是直角三角形呢?由此你又能得到左边的三角形是什么三角形? 如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。证明猜想∵ ∠ C’=900∴ A’B’2= a2+b2∵ a2+b2=c2∴ A’B’ 2=c2∴ A’B’ =c∵ 边长取正值∴ △ ABC ≌△ A’B’C’(SSS)∴ ∠ C= ∠ C’(全等三角形对应角相等)∴ ∠C= 900已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2求证:△ ABC是直角三角形证明:画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=b在△ ABC和△ A’B’C’中∴ △ ABC是直角三角形(直角三角形的定义)一个三角形中两条较短边的平方和等于最长边的平方最长边解:∵152+82=225+64=289而 172=289∴ 152+82=172∴这个三角形是直角三角形∵72+82=113而 102=100∴这个三角形不是
直角三角形 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900勾股定理的逆命题勾股定理互逆命题题设结论互 换互逆命题:题设与结论正好相反的两个命题叫做互逆命题如果把其中一个叫做原命题,那么另一个叫做它的逆命题概念讲解(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的绝对值相等.
(3)对顶角相等.
(4)若ab=0,则a=0.说出下列命题的逆命题.并判断它们的逆命题是否成立。逆命题: 内错角相等,两条直线平行. 逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 逆命题:相等的角是对顶角. 逆命题:若a=0,则ab=0思考:原命题与逆命题的正确性是否一致?成立不成立不成立成立原命题成立时, 逆命题有时成立, 有时不成立成立成立成立不成立定理与逆定理我们已经学习了一些互逆的定理,如:
两直线平行,内错角相等;内错角相等,两直线平行.如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.勾股定理的逆命题勾股定理互逆命题逆定理定理2.指出下列命题中的互逆命题:
(1)直角都相等
(2)等腰三角形两底角相等
(3)如果a+b>0, 那么a>0,b>0
1.判断
(1)每一个命题都有逆命题( )
(2)如果原命题是真命题,那么它的逆命题也 一定是真命题( )
(3)原命题是假命题,但它的逆命题可能是真
命题( )
练一练√╳√相等的角是直角有两个角相等的三角形是等腰三角形如果a+b>0, 那么a>0,b>0
满足 的三个 ,称为勾股数。正整数你能写出常用的勾股数吗?3,4,5; 5,12,13;
6,8,10; 7,24,25;
9,12,15; 8,15,17 ;挑战自我
知识拓展BA、锐角三角形 B、直角三角形C、钝角三角形 D、等边三角形
已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
S四边形ABCD=36本节课我们学习了…1、勾股定理的逆定理2、什么叫做互逆命题、原命题与逆命题、
互逆定理
4、本节课用到了什么数学思想方法?3、勾股定理逆定理的简单应用再 见感谢各位光临指导!
