第2单元因数与倍数重难点检测卷(含答案)数学五年级下册人教版
文档属性
| 名称 | 第2单元因数与倍数重难点检测卷(含答案)数学五年级下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 373.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 20:45:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第2单元因数与倍数重难点检测卷-数学五年级下册人教版
一、选择题
1.下面各数中,同时是2、3、5的倍数的是( )。
A.2705 B.4180 C.3792 D.5730
2.与偶数a相邻的两个偶数是( )。
A.a+1和a-1 B.a+2和a-2 C.a-1和a+2 D.a-1和a+3
3.n是一个大于0的自然数,则2n一定是( )。
A.奇数 B.偶数 C.合数 D.无法确定
4.下面计数器中表示的数是3的倍数的是( )。
A. B.
C. D.
5.A□B是一个三位数,它是3的倍数,已知A+B=7。□中可填的数是( )。
A.4 B.5 C.6 D.7
6.一个数既是15的倍数又是15的因数,这个数是( )。
A.5 B.15 C.30 D.45
二、填空题
7.如果a÷4=b(a,b都是整数),那么a是b的( )数,b是a的( )数。
8.两个质数的和是31,这两个质数的乘积是( )。
9.“7□”是5的倍数,□里可以填( ),“2□5”是3的倍数,□里可以填( )。
10.1~20的自然数中奇数有( )个,质数有( )个。
11.两个质数,它们的和是9,积是14,这两个质数分别是( )和( )。
12.从10,11,12,13,…28,29,30中选择9个自然数填在圆圈中,完成下面的双泡图。
三、判断题
13.15的因数共有4个。其中3和5是质数,其他的都是合数。( )
14.n是质数,那么2n是合数。( )
15.哥德巴赫猜想被誉为“数学皇冠上的明珠。”这个猜想是“是不是所有大于2的偶数都可以表示为两个质数的和呢?”我国数学家陈景润在这一领域取得了举世瞩目的成果。( )
16.最小的合数比最小的质数与最小的非0自然数的积大2。( )
17.M和N都是非零自然数,且M÷N=5,那么M的个位上是0或5。( )
四、解答题
18.育英小学五(3)班有56人,现在要把这些学生分成人数相等的若干个小组(每个小组至少2人),有几种分法?每组最多有多少人?
19.五一班的同学到博物馆参观,男生有15人,女生有20人,如果每组中男生人数相同,女生人数也相同,最多可以分为多少组?每组男生多少人?
20.班长去商店给同学们购买圆珠笔,班长买了若干支,每支3元,最后结账时,收银员说一共149元,班长认为收银员算得不对。你同意班长的意见吗?为什么?
21.一个长方形的面积是36平方厘米,并且长和宽的长度都是整厘米数。这个长方形的周长最长是多少厘米?
22.玩转盘游戏。
(1)转动指针,指针指向合数,贝贝获胜;指向质数,则甜甜获胜。这个游戏规则公平吗? 为什么?
(2)如上图,指针分别指向下列条件中的数,则甜甜胜,如果你是甜甜,你会选择哪一种?请说明理由。
①大于6的数 ②不是3的倍数的数 ③有因数2的数
参考答案:
1.D
【分析】根据2、3、5的倍数的特征可知,同时是2、3、5的倍数的数,个位上必须是0且各个数位上的数字之和是3的倍数。据此解答。
【详解】A.2705的个位是5,不符合题意;
B.4180的个位是0,4+1+8=13,13不是3的倍数,不符合题意;
C.3792的个位是2,不符合题意;
D.5730的个位是0,5+7+3=15,15是3的倍数,符合题意。
所以,同时是2、3、5的倍数的是5730。
故答案为:D
【点睛】本题考查了2、3、5的倍数特征,要熟练掌握并运用。
2.B
【分析】相邻的两个偶数之间相差2, 因此中间偶数分别-2和+2是与这个偶数相邻的两个偶数,据此分析。
【详解】与偶数a相邻的两个偶数是(a+2)和(a-2)。
故答案为:B
【点睛】关键是理解奇数、偶数的分类标准,整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
3.B
【分析】整数中,是2的倍数的数叫作偶数(0也是偶数),不是2的倍数的数叫作奇数;一个数,如果只有1和它本身两个因数,那么这样的数叫作质数;一个数,如果除了1和它本身还有别的因数,那么这样的数叫作合数,据此解答。
【详解】当n=1时,2n=2×1=2,2是偶数也是质数;当n=4时,2n=2×4=8,8是偶数也是合数;如果n是一个大于0的自然数,那么2n一定是2的倍数,所以2n一定是偶数。
故答案为:B
【点睛】掌握奇数、偶数、质数、合数的意义是解答题目的关键。
4.B
【分析】先根据数的组成,写出4个选项中的整数,再利用3的倍数的特征:各位上的数字之和是3的倍数,这个数就是3的倍数,据此判断即可得解。
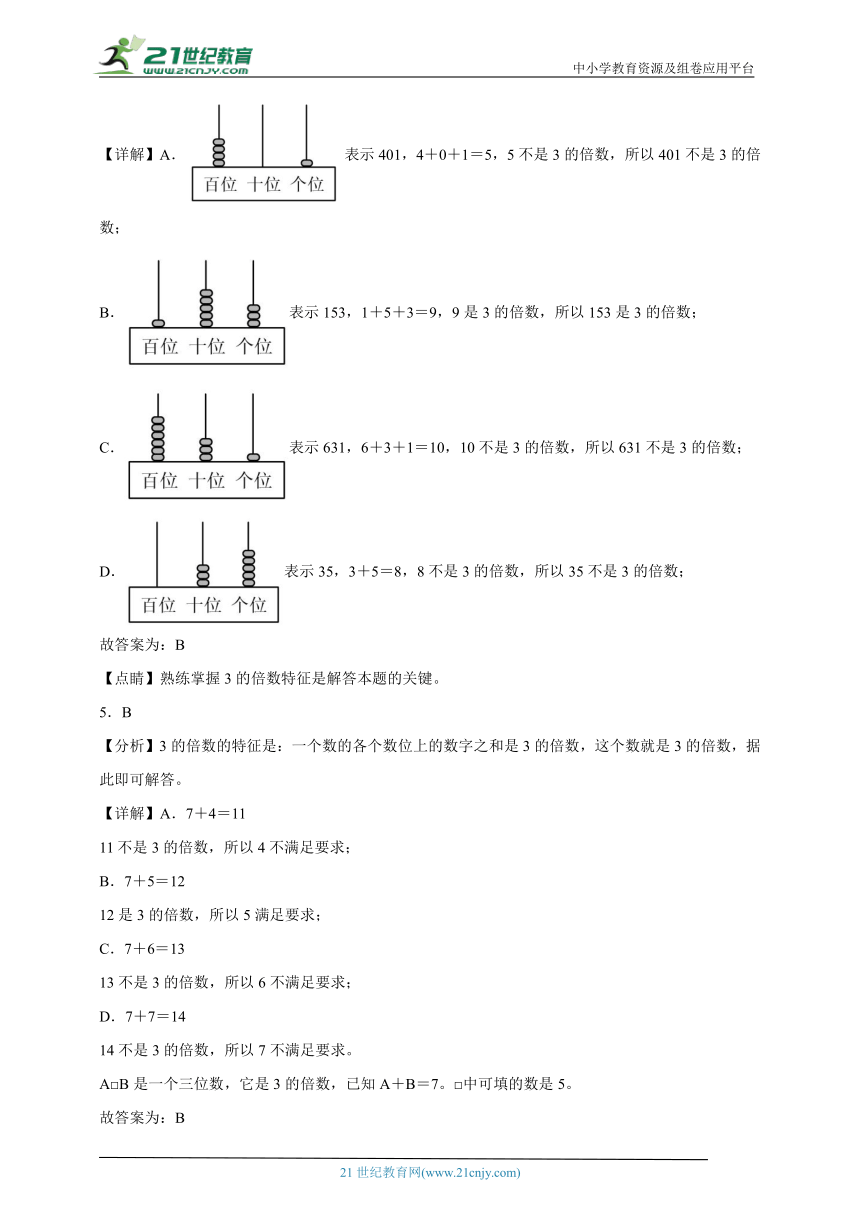
【详解】A.表示401,4+0+1=5,5不是3的倍数,所以401不是3的倍数;
B.表示153,1+5+3=9,9是3的倍数,所以153是3的倍数;
C.表示631,6+3+1=10,10不是3的倍数,所以631不是3的倍数;
D.表示35,3+5=8,8不是3的倍数,所以35不是3的倍数;
故答案为:B
【点睛】熟练掌握3的倍数特征是解答本题的关键。
5.B
【分析】3的倍数的特征是:一个数的各个数位上的数字之和是3的倍数,这个数就是3的倍数,据此即可解答。
【详解】A.7+4=11
11不是3的倍数,所以4不满足要求;
B.7+5=12
12是3的倍数,所以5满足要求;
C.7+6=13
13不是3的倍数,所以6不满足要求;
D.7+7=14
14不是3的倍数,所以7不满足要求。
A□B是一个三位数,它是3的倍数,已知A+B=7。□中可填的数是5。
故答案为:B
【点睛】熟练掌握3的倍数特征是解决问题的关键。
6.B
【分析】求一个数的因数时,就用这个数从1开始去整除,一直除到除数和商交换位置或除数和商相同为止,除数和商都是被除数的因数,重复的因数只写一个,先求出15的所有因数,再从15的因数中找出15的倍数,据此解答。
【详解】15÷1=15
15÷3=5
则15的因数有:1、3、5、15,其中15又是15的倍数。
则一个数既是15的倍数又是15的因数,这个数是15。
故答案为:B
【点睛】掌握求一个数因数的方法,明确一个数的最大因数和最小倍数都是这个数本身。
7. 倍 因
【分析】根据因数和倍数的意义:如果数a能被是b整除(b≠0),a就叫作b的倍数,b就叫作a的因数;据此解答。
【详解】a÷4=b(a,b都是整数),那么a是b的倍数,b是a的因数。
【点睛】熟练掌握因数与倍数的意义是解答本题的关键。
8.58
【分析】因为奇数+奇数=偶数,奇数+偶数=奇数。而题中已知这两个质数的和是31,31是奇数,所以这两个质数中一定有一个质数是偶数,偶数中只有2是质数,由此即可求出另外一个质数,进而求得它们的乘积。
【详解】31=2+29
2×29=58
即这两个质数的乘积是58。
【点睛】此题根据和的奇偶性先确定其中一个质数是解题的关键。
9. 0、5 2、5、8
【分析】5的倍数特征:个位数是0或5;3的倍数特征:各个数位上的数字和是3的倍数;据此解答。
【详解】由分析可得:“7□”是5的倍数,根据5的倍数的特征,□里可以填0或5;
“2□5”是3的倍数,根据3的倍数的特征,
2+5=7
7+2=9
7+5=12
7+8=15
9,12,15都是3的倍数,所以□里可以填2、5、8。
【点睛】本题熟练掌握3、5的倍数的特征是解决此题的关键。
10. 10 8
【分析】整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。
【详解】1~20的自然数中奇数有1、3、5、7、9、11、13、15、17、19,共10个,质数有2、3、5、7、11、13、17、19,共8个
【点睛】关键是理解奇数、偶数、质数、合数的分类标准。
11. 2 7
【分析】根据质数的定义可得,9以内的质数为:2、3、5、7,因为9=2+7,2×7=14,据此解答即可。
【详解】9=2+7
14=2×7
两个质数,它们的和是9,积是14,这两个质数分别是2和7。
【点睛】此题考查了质数的应用,关键是明确质数的定义即可。
12.见详解
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
【详解】如图:
(答案不唯一)
【点睛】本题考查奇数、合数的意义及应用,注意中间三个要填既是奇数又是合数的数。
13.×
【分析】15的因数有1,3,5,15。其中1既不是质数,也不是合数;3和5是质数;15是合数。据此判断即可。
【详解】15的因数共有4个。其中3和5是质数,15是合数,1不是合数。即原题说法错误。
故答案为:×
14.√
【分析】在所有比1大的整数中,除了1和它本身以外,不再有别的因数,这种整数叫做质数;合数是除了1和它本身还能被其他的正整数整除的正整数,除2之外的偶数都是合数;据此解答。
【详解】n是质数,则n是大于1的整数,那么2n是除2之外的偶数,所以2n是合数;故说法正确。
【点睛】此题考查了质数与合数的认识,关键理解字母代表的数的意义。
15.√
【分析】在自然数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数;一个数只有1和它本身两个因数,这个数叫做质数。一个数除了1和它本身两个因数,还有其他的因数,这个数叫做合数。据此解答。
【详解】哥德巴赫猜想被称作数学皇冠上的明珠,这个猜想是这样的:任何一个大于2的偶数都可以表示成两个质数之和,我国著名数学家陈景润在这个猜想的基础上取得重大突破。他证明了:任何一个大于2的偶数都可以表示成两个质数之和。
例如:10=3+7
10是偶数,3和7都是质数。
所以原题干说法正确。
故答案为:√
【点睛】本题主要考查了质数、偶数的认识。
16.√
【分析】分别找出最小的合数、最小的质数与最小的非0自然数是多少,根据题意计算即可。
【详解】最小的合数是4,最小的质数是2,最小的非0自然数是1,4-2×1=2。
故答案为:正确。
【点睛】解答此题的关键是找准最小的合数、最小的质数与最小的非0自然数。需要在理解的基础上熟记。
17.√
【分析】因为M÷N=5,则M÷5=N,M和N都是非零自然数,所以M是5的倍数;再根据5的倍数特征:个位上的数字是0或5的数是5的倍数,所以M的个位上是0或5,据此解答。
【详解】根据分析可知,M和N都是非零自然数,且M÷N=5,那么M的个位上是0或5。
故答案为:√
18.6种;28人
【分析】把这些学生分成人数相等的若干个小组,说明满足条件的小组人数是56的因数,先找出56的所有因数,再解答即可。
【详解】56=1×56=2×28=4×14=7×8
56的因数有:1、2、4、14、78、14、28、56,共8个,因为每组至少有2人,所以只有6种分法。
答:有6种分法,每组最多有28人。
【点睛】本题考查因数,解答本题的关键是掌握求一个数的因数的方法。
19.5组;3人
【分析】由题意可知:分组后每个小组的男生和女生人数分别相等,要求最多能分成几个小组,只要求出15和20的最大公因数即可解决问题。
【详解】15=5×3
20=5×2×2
所以15和20的最大公因数是5,每组男生3人。
答:最多可以分成5组,每组男生3人。
【点睛】灵活运用最大公因数的求解方法来解决实际问题。
20.同意;因为149不是3的倍数
【分析】根据题意可知,每支圆珠笔的单价×圆珠笔的支数=总价,因为每支圆珠笔3元,圆珠笔的支数是整数,所以总价一定是3的倍数, 3的倍数特征:各个数位上的数字和是3的倍数;据此判断149是否是3的倍数即可。
【详解】1+4+9=14
14÷3=4……2
所以14不是3的倍数,149不是3的倍数。
答:我同意班长的意见,因为149不是3的倍数。
【点睛】本题考查了3的倍数特征的应用。
21.74厘米
【分析】,当长方形的面积一定时,长和宽的差越大,周长越长,据此解答即可。
【详解】根据长方形的面积是36平方厘米,可知当长是36厘米,宽是1厘米时,这个长方形周长最大,则:
(厘米)
答:这个长方形的周长最长是74厘米。
【点睛】本题考查因数,解答本题的关键是掌握求一个数的因数的计算方法。
22.(1)不公平;见详解
(2)②;见详解
【分析】(1)一个数,如果只有1和它本身两个因数,那么这样的数叫做质数;一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
从1~10中分别找出质数和合数,比较数量的多少,如果数量不一样多,那么数量多的,获胜的可能性就大,游戏规则就不公平;反之,如果数量一样多,获胜的可能性相等,游戏规则就公平。
(2)2的倍数特征:个位上是0、2、4、6、8的数;
3的倍数特征:各个数位上的数字相加,和要能被3整除。
从1~10中分别找出符合三个条件的数,比较数量的多少,选择数量最多的选项,这样获胜的可能性最大。
【详解】(1)1~10中的合数有:4、6、8、9、10,一共有5个;
1~10中的质数有:2、3、5、7,一共有4个;
5>4
答:这个游戏规则不公平,1~10中的合数比质数多,所以转动指针,指针指向合数的可能性大,贝贝获胜的可能性大。
(2)1~10中,大于6的数有:7、8、9、10,一共有4个;
1~10中,不是3的倍数的数有:1、2、4、5、7、8、10,一共有7个;
1~10中,有因数2的数有:2、4、6、8、10,一共有5个;
7>5>4
不是3的倍数的数的个数最多,获胜的可能性最大。
答:如果我是甜甜,我会选择②不是3的倍数的数。
【点睛】本题考查可能性和游戏的公平性知识,根据事件数量的多少判断可能性的大小,要使游戏公平,发生的可能性必须相等。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第2单元因数与倍数重难点检测卷-数学五年级下册人教版
一、选择题
1.下面各数中,同时是2、3、5的倍数的是( )。
A.2705 B.4180 C.3792 D.5730
2.与偶数a相邻的两个偶数是( )。
A.a+1和a-1 B.a+2和a-2 C.a-1和a+2 D.a-1和a+3
3.n是一个大于0的自然数,则2n一定是( )。
A.奇数 B.偶数 C.合数 D.无法确定
4.下面计数器中表示的数是3的倍数的是( )。
A. B.
C. D.
5.A□B是一个三位数,它是3的倍数,已知A+B=7。□中可填的数是( )。
A.4 B.5 C.6 D.7
6.一个数既是15的倍数又是15的因数,这个数是( )。
A.5 B.15 C.30 D.45
二、填空题
7.如果a÷4=b(a,b都是整数),那么a是b的( )数,b是a的( )数。
8.两个质数的和是31,这两个质数的乘积是( )。
9.“7□”是5的倍数,□里可以填( ),“2□5”是3的倍数,□里可以填( )。
10.1~20的自然数中奇数有( )个,质数有( )个。
11.两个质数,它们的和是9,积是14,这两个质数分别是( )和( )。
12.从10,11,12,13,…28,29,30中选择9个自然数填在圆圈中,完成下面的双泡图。
三、判断题
13.15的因数共有4个。其中3和5是质数,其他的都是合数。( )
14.n是质数,那么2n是合数。( )
15.哥德巴赫猜想被誉为“数学皇冠上的明珠。”这个猜想是“是不是所有大于2的偶数都可以表示为两个质数的和呢?”我国数学家陈景润在这一领域取得了举世瞩目的成果。( )
16.最小的合数比最小的质数与最小的非0自然数的积大2。( )
17.M和N都是非零自然数,且M÷N=5,那么M的个位上是0或5。( )
四、解答题
18.育英小学五(3)班有56人,现在要把这些学生分成人数相等的若干个小组(每个小组至少2人),有几种分法?每组最多有多少人?
19.五一班的同学到博物馆参观,男生有15人,女生有20人,如果每组中男生人数相同,女生人数也相同,最多可以分为多少组?每组男生多少人?
20.班长去商店给同学们购买圆珠笔,班长买了若干支,每支3元,最后结账时,收银员说一共149元,班长认为收银员算得不对。你同意班长的意见吗?为什么?
21.一个长方形的面积是36平方厘米,并且长和宽的长度都是整厘米数。这个长方形的周长最长是多少厘米?
22.玩转盘游戏。
(1)转动指针,指针指向合数,贝贝获胜;指向质数,则甜甜获胜。这个游戏规则公平吗? 为什么?
(2)如上图,指针分别指向下列条件中的数,则甜甜胜,如果你是甜甜,你会选择哪一种?请说明理由。
①大于6的数 ②不是3的倍数的数 ③有因数2的数
参考答案:
1.D
【分析】根据2、3、5的倍数的特征可知,同时是2、3、5的倍数的数,个位上必须是0且各个数位上的数字之和是3的倍数。据此解答。
【详解】A.2705的个位是5,不符合题意;
B.4180的个位是0,4+1+8=13,13不是3的倍数,不符合题意;
C.3792的个位是2,不符合题意;
D.5730的个位是0,5+7+3=15,15是3的倍数,符合题意。
所以,同时是2、3、5的倍数的是5730。
故答案为:D
【点睛】本题考查了2、3、5的倍数特征,要熟练掌握并运用。
2.B
【分析】相邻的两个偶数之间相差2, 因此中间偶数分别-2和+2是与这个偶数相邻的两个偶数,据此分析。
【详解】与偶数a相邻的两个偶数是(a+2)和(a-2)。
故答案为:B
【点睛】关键是理解奇数、偶数的分类标准,整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
3.B
【分析】整数中,是2的倍数的数叫作偶数(0也是偶数),不是2的倍数的数叫作奇数;一个数,如果只有1和它本身两个因数,那么这样的数叫作质数;一个数,如果除了1和它本身还有别的因数,那么这样的数叫作合数,据此解答。
【详解】当n=1时,2n=2×1=2,2是偶数也是质数;当n=4时,2n=2×4=8,8是偶数也是合数;如果n是一个大于0的自然数,那么2n一定是2的倍数,所以2n一定是偶数。
故答案为:B
【点睛】掌握奇数、偶数、质数、合数的意义是解答题目的关键。
4.B
【分析】先根据数的组成,写出4个选项中的整数,再利用3的倍数的特征:各位上的数字之和是3的倍数,这个数就是3的倍数,据此判断即可得解。
【详解】A.表示401,4+0+1=5,5不是3的倍数,所以401不是3的倍数;
B.表示153,1+5+3=9,9是3的倍数,所以153是3的倍数;
C.表示631,6+3+1=10,10不是3的倍数,所以631不是3的倍数;
D.表示35,3+5=8,8不是3的倍数,所以35不是3的倍数;
故答案为:B
【点睛】熟练掌握3的倍数特征是解答本题的关键。
5.B
【分析】3的倍数的特征是:一个数的各个数位上的数字之和是3的倍数,这个数就是3的倍数,据此即可解答。
【详解】A.7+4=11
11不是3的倍数,所以4不满足要求;
B.7+5=12
12是3的倍数,所以5满足要求;
C.7+6=13
13不是3的倍数,所以6不满足要求;
D.7+7=14
14不是3的倍数,所以7不满足要求。
A□B是一个三位数,它是3的倍数,已知A+B=7。□中可填的数是5。
故答案为:B
【点睛】熟练掌握3的倍数特征是解决问题的关键。
6.B
【分析】求一个数的因数时,就用这个数从1开始去整除,一直除到除数和商交换位置或除数和商相同为止,除数和商都是被除数的因数,重复的因数只写一个,先求出15的所有因数,再从15的因数中找出15的倍数,据此解答。
【详解】15÷1=15
15÷3=5
则15的因数有:1、3、5、15,其中15又是15的倍数。
则一个数既是15的倍数又是15的因数,这个数是15。
故答案为:B
【点睛】掌握求一个数因数的方法,明确一个数的最大因数和最小倍数都是这个数本身。
7. 倍 因
【分析】根据因数和倍数的意义:如果数a能被是b整除(b≠0),a就叫作b的倍数,b就叫作a的因数;据此解答。
【详解】a÷4=b(a,b都是整数),那么a是b的倍数,b是a的因数。
【点睛】熟练掌握因数与倍数的意义是解答本题的关键。
8.58
【分析】因为奇数+奇数=偶数,奇数+偶数=奇数。而题中已知这两个质数的和是31,31是奇数,所以这两个质数中一定有一个质数是偶数,偶数中只有2是质数,由此即可求出另外一个质数,进而求得它们的乘积。
【详解】31=2+29
2×29=58
即这两个质数的乘积是58。
【点睛】此题根据和的奇偶性先确定其中一个质数是解题的关键。
9. 0、5 2、5、8
【分析】5的倍数特征:个位数是0或5;3的倍数特征:各个数位上的数字和是3的倍数;据此解答。
【详解】由分析可得:“7□”是5的倍数,根据5的倍数的特征,□里可以填0或5;
“2□5”是3的倍数,根据3的倍数的特征,
2+5=7
7+2=9
7+5=12
7+8=15
9,12,15都是3的倍数,所以□里可以填2、5、8。
【点睛】本题熟练掌握3、5的倍数的特征是解决此题的关键。
10. 10 8
【分析】整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。
【详解】1~20的自然数中奇数有1、3、5、7、9、11、13、15、17、19,共10个,质数有2、3、5、7、11、13、17、19,共8个
【点睛】关键是理解奇数、偶数、质数、合数的分类标准。
11. 2 7
【分析】根据质数的定义可得,9以内的质数为:2、3、5、7,因为9=2+7,2×7=14,据此解答即可。
【详解】9=2+7
14=2×7
两个质数,它们的和是9,积是14,这两个质数分别是2和7。
【点睛】此题考查了质数的应用,关键是明确质数的定义即可。
12.见详解
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
【详解】如图:
(答案不唯一)
【点睛】本题考查奇数、合数的意义及应用,注意中间三个要填既是奇数又是合数的数。
13.×
【分析】15的因数有1,3,5,15。其中1既不是质数,也不是合数;3和5是质数;15是合数。据此判断即可。
【详解】15的因数共有4个。其中3和5是质数,15是合数,1不是合数。即原题说法错误。
故答案为:×
14.√
【分析】在所有比1大的整数中,除了1和它本身以外,不再有别的因数,这种整数叫做质数;合数是除了1和它本身还能被其他的正整数整除的正整数,除2之外的偶数都是合数;据此解答。
【详解】n是质数,则n是大于1的整数,那么2n是除2之外的偶数,所以2n是合数;故说法正确。
【点睛】此题考查了质数与合数的认识,关键理解字母代表的数的意义。
15.√
【分析】在自然数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数;一个数只有1和它本身两个因数,这个数叫做质数。一个数除了1和它本身两个因数,还有其他的因数,这个数叫做合数。据此解答。
【详解】哥德巴赫猜想被称作数学皇冠上的明珠,这个猜想是这样的:任何一个大于2的偶数都可以表示成两个质数之和,我国著名数学家陈景润在这个猜想的基础上取得重大突破。他证明了:任何一个大于2的偶数都可以表示成两个质数之和。
例如:10=3+7
10是偶数,3和7都是质数。
所以原题干说法正确。
故答案为:√
【点睛】本题主要考查了质数、偶数的认识。
16.√
【分析】分别找出最小的合数、最小的质数与最小的非0自然数是多少,根据题意计算即可。
【详解】最小的合数是4,最小的质数是2,最小的非0自然数是1,4-2×1=2。
故答案为:正确。
【点睛】解答此题的关键是找准最小的合数、最小的质数与最小的非0自然数。需要在理解的基础上熟记。
17.√
【分析】因为M÷N=5,则M÷5=N,M和N都是非零自然数,所以M是5的倍数;再根据5的倍数特征:个位上的数字是0或5的数是5的倍数,所以M的个位上是0或5,据此解答。
【详解】根据分析可知,M和N都是非零自然数,且M÷N=5,那么M的个位上是0或5。
故答案为:√
18.6种;28人
【分析】把这些学生分成人数相等的若干个小组,说明满足条件的小组人数是56的因数,先找出56的所有因数,再解答即可。
【详解】56=1×56=2×28=4×14=7×8
56的因数有:1、2、4、14、78、14、28、56,共8个,因为每组至少有2人,所以只有6种分法。
答:有6种分法,每组最多有28人。
【点睛】本题考查因数,解答本题的关键是掌握求一个数的因数的方法。
19.5组;3人
【分析】由题意可知:分组后每个小组的男生和女生人数分别相等,要求最多能分成几个小组,只要求出15和20的最大公因数即可解决问题。
【详解】15=5×3
20=5×2×2
所以15和20的最大公因数是5,每组男生3人。
答:最多可以分成5组,每组男生3人。
【点睛】灵活运用最大公因数的求解方法来解决实际问题。
20.同意;因为149不是3的倍数
【分析】根据题意可知,每支圆珠笔的单价×圆珠笔的支数=总价,因为每支圆珠笔3元,圆珠笔的支数是整数,所以总价一定是3的倍数, 3的倍数特征:各个数位上的数字和是3的倍数;据此判断149是否是3的倍数即可。
【详解】1+4+9=14
14÷3=4……2
所以14不是3的倍数,149不是3的倍数。
答:我同意班长的意见,因为149不是3的倍数。
【点睛】本题考查了3的倍数特征的应用。
21.74厘米
【分析】,当长方形的面积一定时,长和宽的差越大,周长越长,据此解答即可。
【详解】根据长方形的面积是36平方厘米,可知当长是36厘米,宽是1厘米时,这个长方形周长最大,则:
(厘米)
答:这个长方形的周长最长是74厘米。
【点睛】本题考查因数,解答本题的关键是掌握求一个数的因数的计算方法。
22.(1)不公平;见详解
(2)②;见详解
【分析】(1)一个数,如果只有1和它本身两个因数,那么这样的数叫做质数;一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
从1~10中分别找出质数和合数,比较数量的多少,如果数量不一样多,那么数量多的,获胜的可能性就大,游戏规则就不公平;反之,如果数量一样多,获胜的可能性相等,游戏规则就公平。
(2)2的倍数特征:个位上是0、2、4、6、8的数;
3的倍数特征:各个数位上的数字相加,和要能被3整除。
从1~10中分别找出符合三个条件的数,比较数量的多少,选择数量最多的选项,这样获胜的可能性最大。
【详解】(1)1~10中的合数有:4、6、8、9、10,一共有5个;
1~10中的质数有:2、3、5、7,一共有4个;
5>4
答:这个游戏规则不公平,1~10中的合数比质数多,所以转动指针,指针指向合数的可能性大,贝贝获胜的可能性大。
(2)1~10中,大于6的数有:7、8、9、10,一共有4个;
1~10中,不是3的倍数的数有:1、2、4、5、7、8、10,一共有7个;
1~10中,有因数2的数有:2、4、6、8、10,一共有5个;
7>5>4
不是3的倍数的数的个数最多,获胜的可能性最大。
答:如果我是甜甜,我会选择②不是3的倍数的数。
【点睛】本题考查可能性和游戏的公平性知识,根据事件数量的多少判断可能性的大小,要使游戏公平,发生的可能性必须相等。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
