生活中的轴对称
图片预览







文档简介
课件36张PPT。生活中的轴对称 在现实生活中,和谐美丽的对称形式随处可见。让我们来认识这奇妙的数学现象吧!12.1轴对称12.1轴对称轴对称图形如果一个图形沿某条直线翻折,直线两旁的部分能够互相重合,那么就称这样的图形为轴对称图形.
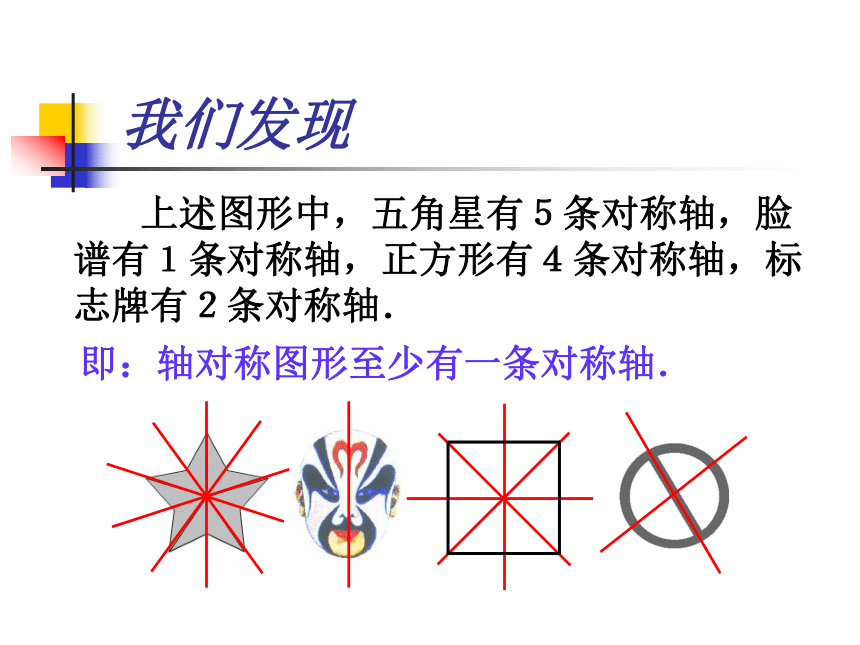
这条直线叫做这个图形的对称轴.这个数学概念,你知道吗?观察思考1 右边的图形中哪些是轴对称图形?若是,你能画出它们的对称轴吗?⑴⑵⑶⑷⑸ 上述图形中,五角星有5条对称轴,脸谱有1条对称轴,正方形有4条对称轴,标志牌有2条对称轴.我们发现即:轴对称图形至少有一条对称轴.联系实际1 你能举出生活中轴对称图形的例子吗?试找出它们的对称轴.快点展开想象的翅膀!轴对称图形 下面的图形中哪个是轴对称图形?它有几条对称轴?无数条线段和角是轴对称图形吗?
如果是,就说出它们的对称轴!线段和角都是轴对称图形。线段的对称轴是线段的垂直平分线。角的对称轴是角的平分线所在的直线。那么圆的对称轴是什么呢?圆的对称轴是圆的直径所在的直线。有无数条!思考练习1 请在下列一组图形符号中找出它们所蕴含的内在规律,然后在空白处填上恰当的图形. 图片一图片二观察以下两组图片,看有什么相同的特点:两个图形成轴对称把一个图形沿着某一直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称.
这条直线称为对称轴.
两个图形中的对应点(即两图形重合时互相重合的点)叫做关于这条直线的对称点.
如果一点在对称轴上它的对称点就是它本身.黑格尔说:“审美带有令人解放的性质”。
一切事物倘能与美相接便立即会焕发出动人的光彩,
这正是美的神奇力量之所在。
在现实生活中,常常可以看到对称美。
“对称”既是数学概念,
又是美学的一个重要概念。操作 将一张长方形纸片沿着直线l对折成两层纸,
然后在两层纸上挖去一个三角形纸片,再将两层
纸平摊,就得到两个三角形:
△ABC和△A’B’C’.思考:△ABC和△A’B’C’是否关于
直线l 对称?为什么?2. 线段AB和A’B’是否关于直线l对称?
为什么?BC和B’C’,CA和C’A’呢?3. 点A和点B’关于直线l的
对称点各是哪一点?点A在对称轴上,
所以它的对称点A’与它自身重合。
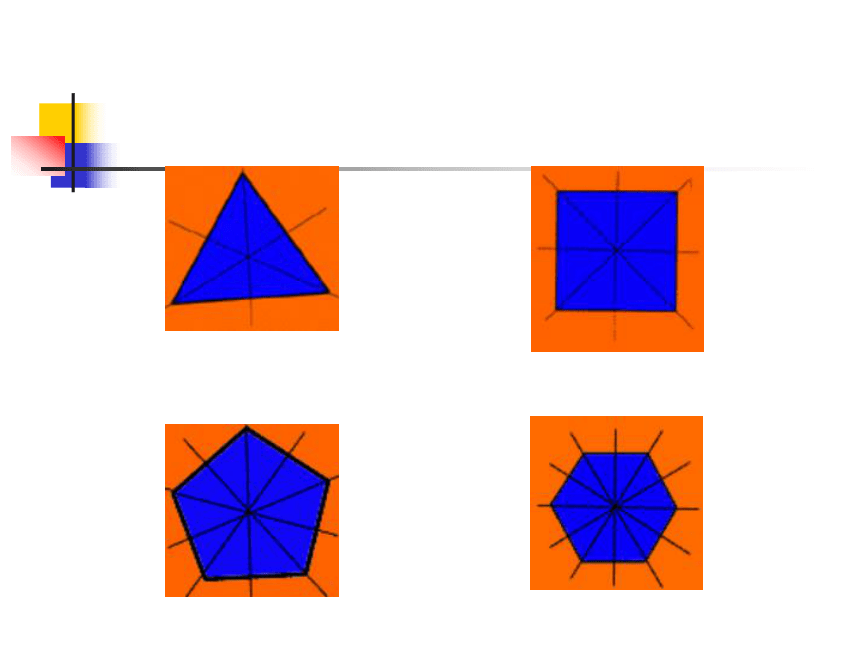
可以说, 点A 的对称点就是它本身。观察思考这三组图形中,两个图形关于直线对称的有哪些组?①②③区别与联系轴对称图形和关于某条直线对称是两个不同的概念,它们之间既有区别又有联系. 区别:轴对称图形是指一个具有特殊形状的图形,而关于某条直线对称是指两个图形之间的一种位置关系. 联系:关于某条直线对称与轴对称图形都有对称轴.如果把关于某条直线对称的两个图形看成一个整体,那么它就是一个轴对称图形;如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线对称。区别与联系探索与思考1 正三角形、正方形、正五边形、正六边形都是轴对称图形吗?它们各有几条对称轴?那么,正n边形(n≥3,且为整数)呢?若是,你能找出它们的对称轴吗?查看结果探索与思考2图1图2观察下图中的两个三角形,它们是否关于直线 对称?你能说说其中的道理吗?课堂小结 请大家回顾以下,这堂课我们学习了哪些内容?1.认识了轴对称图形,并会找出其对称轴;2.认识了两个图形关于某条直线对称,会找其对称轴和对称点;课后作业想一想,我们学习过的简单几何图形中有哪些是轴对称图形?并尝试找出它们的对称轴.
探索与思考2的结果对你有什么启发吗?和你的小组成员一起,尝试讨论轴对称图形还有哪些性质?十全十美看看这几个汉字有什么特点?课堂表现大众雪铁龙福特林肯长城汽车奔驰大宇现代返回丰田下列字母中有哪些是轴对称图形,又有几条对称轴?观察思考返回WTONBA SOSMVP 观察思考 它们中有哪些是轴对称图形,又有几条对称轴?返回0 1 2 3 4
5 6 7 8 9观察思考 美 天 田 申
王 中 士 莱下面的汉字(黑体)若看作是图形,那么它们是轴对称图形吗?你还能想出更多的吗?返回 下列图形是我国四大银行的标志,从几何的性质考虑,哪一个与其他三个不同?请指出这个图形,并说明你的理由.①②③④返回3456n正多边形的边数与对称轴条数的关系返回如图,E、F是公路AB 同一侧的两个村子,现在要在公路上修建一个汽车站,问 这个汽车站建立在公路上的哪一点,才能使它到E、F两村总路最短?EFBACC’EC=E’C ,EC’=E’C’EC+CF =E’C+ CF =E’F而 EC’+C’F=E’C’+C’FE’C’+C’F>E’F所以EC’+C’F>EC +CF
这条直线叫做这个图形的对称轴.这个数学概念,你知道吗?观察思考1 右边的图形中哪些是轴对称图形?若是,你能画出它们的对称轴吗?⑴⑵⑶⑷⑸ 上述图形中,五角星有5条对称轴,脸谱有1条对称轴,正方形有4条对称轴,标志牌有2条对称轴.我们发现即:轴对称图形至少有一条对称轴.联系实际1 你能举出生活中轴对称图形的例子吗?试找出它们的对称轴.快点展开想象的翅膀!轴对称图形 下面的图形中哪个是轴对称图形?它有几条对称轴?无数条线段和角是轴对称图形吗?
如果是,就说出它们的对称轴!线段和角都是轴对称图形。线段的对称轴是线段的垂直平分线。角的对称轴是角的平分线所在的直线。那么圆的对称轴是什么呢?圆的对称轴是圆的直径所在的直线。有无数条!思考练习1 请在下列一组图形符号中找出它们所蕴含的内在规律,然后在空白处填上恰当的图形. 图片一图片二观察以下两组图片,看有什么相同的特点:两个图形成轴对称把一个图形沿着某一直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称.
这条直线称为对称轴.
两个图形中的对应点(即两图形重合时互相重合的点)叫做关于这条直线的对称点.
如果一点在对称轴上它的对称点就是它本身.黑格尔说:“审美带有令人解放的性质”。
一切事物倘能与美相接便立即会焕发出动人的光彩,
这正是美的神奇力量之所在。
在现实生活中,常常可以看到对称美。
“对称”既是数学概念,
又是美学的一个重要概念。操作 将一张长方形纸片沿着直线l对折成两层纸,
然后在两层纸上挖去一个三角形纸片,再将两层
纸平摊,就得到两个三角形:
△ABC和△A’B’C’.思考:△ABC和△A’B’C’是否关于
直线l 对称?为什么?2. 线段AB和A’B’是否关于直线l对称?
为什么?BC和B’C’,CA和C’A’呢?3. 点A和点B’关于直线l的
对称点各是哪一点?点A在对称轴上,
所以它的对称点A’与它自身重合。
可以说, 点A 的对称点就是它本身。观察思考这三组图形中,两个图形关于直线对称的有哪些组?①②③区别与联系轴对称图形和关于某条直线对称是两个不同的概念,它们之间既有区别又有联系. 区别:轴对称图形是指一个具有特殊形状的图形,而关于某条直线对称是指两个图形之间的一种位置关系. 联系:关于某条直线对称与轴对称图形都有对称轴.如果把关于某条直线对称的两个图形看成一个整体,那么它就是一个轴对称图形;如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线对称。区别与联系探索与思考1 正三角形、正方形、正五边形、正六边形都是轴对称图形吗?它们各有几条对称轴?那么,正n边形(n≥3,且为整数)呢?若是,你能找出它们的对称轴吗?查看结果探索与思考2图1图2观察下图中的两个三角形,它们是否关于直线 对称?你能说说其中的道理吗?课堂小结 请大家回顾以下,这堂课我们学习了哪些内容?1.认识了轴对称图形,并会找出其对称轴;2.认识了两个图形关于某条直线对称,会找其对称轴和对称点;课后作业想一想,我们学习过的简单几何图形中有哪些是轴对称图形?并尝试找出它们的对称轴.
探索与思考2的结果对你有什么启发吗?和你的小组成员一起,尝试讨论轴对称图形还有哪些性质?十全十美看看这几个汉字有什么特点?课堂表现大众雪铁龙福特林肯长城汽车奔驰大宇现代返回丰田下列字母中有哪些是轴对称图形,又有几条对称轴?观察思考返回WTONBA SOSMVP 观察思考 它们中有哪些是轴对称图形,又有几条对称轴?返回0 1 2 3 4
5 6 7 8 9观察思考 美 天 田 申
王 中 士 莱下面的汉字(黑体)若看作是图形,那么它们是轴对称图形吗?你还能想出更多的吗?返回 下列图形是我国四大银行的标志,从几何的性质考虑,哪一个与其他三个不同?请指出这个图形,并说明你的理由.①②③④返回3456n正多边形的边数与对称轴条数的关系返回如图,E、F是公路AB 同一侧的两个村子,现在要在公路上修建一个汽车站,问 这个汽车站建立在公路上的哪一点,才能使它到E、F两村总路最短?EFBACC’EC=E’C ,EC’=E’C’EC+CF =E’C+ CF =E’F而 EC’+C’F=E’C’+C’FE’C’+C’F>E’F所以EC’+C’F>EC +CF
