3.1.3 圆柱的体积 同步练习 人教版数学 六年级下册(含解析)
文档属性
| 名称 | 3.1.3 圆柱的体积 同步练习 人教版数学 六年级下册(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 323.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 15:46:30 | ||
图片预览


文档简介
3.1.3 圆柱的体积 同步练习 人教版数学 六年级下册
一、填空题(共5小题)
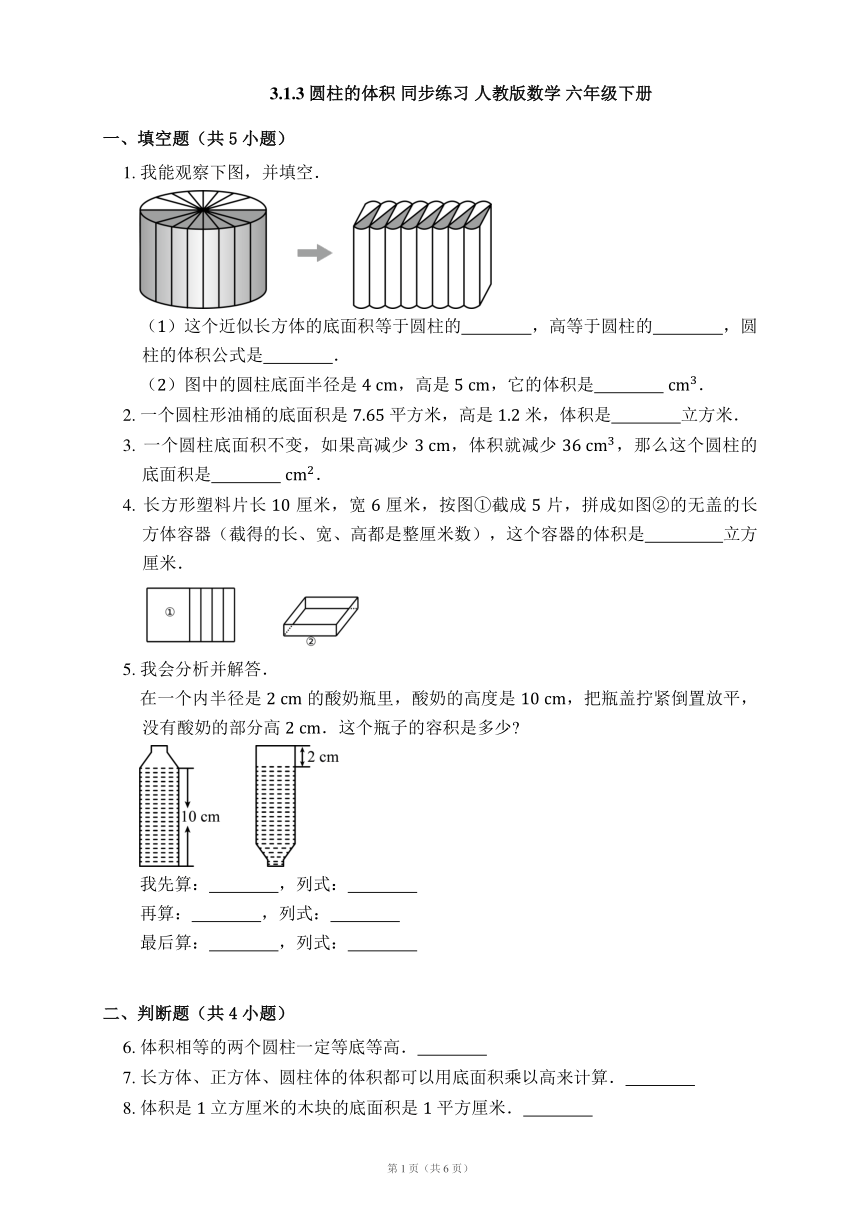
1. 我能观察下图,并填空.
()这个近似长方体的底面积等于圆柱的 ,高等于圆柱的 ,圆柱的体积公式是 .
()图中的圆柱底面半径是 ,高是 ,它的体积是 .
2. 一个圆柱形油桶的底面积是 平方米,高是 米,体积是 立方米.
3. 一个圆柱底面积不变,如果高减少 ,体积就减少 ,那么这个圆柱的底面积是 .
4. 长方形塑料片长 厘米,宽 厘米,按图①截成 片,拼成如图②的无盖的长方体容器(截得的长、宽、高都是整厘米数),这个容器的体积是 立方厘米.
5. 我会分析并解答.
在一个内半径是 的酸奶瓶里,酸奶的高度是 ,把瓶盖拧紧倒置放平,没有酸奶的部分高 .这个瓶子的容积是多少
我先算: ,列式:
再算: ,列式:
最后算: ,列式:
二、判断题(共4小题)
6. 体积相等的两个圆柱一定等底等高.
7. 长方体、正方体、圆柱体的体积都可以用底面积乘以高来计算.
8. 体积是 立方厘米的木块的底面积是 平方厘米.
9. 一个圆柱的高扩大为原来的 倍,底面积缩小为原来的 ,它的体积不变.
三、选择题(共6小题)
10. 若圆柱的底面半径和高都扩大到原来的 倍,则它的体积扩大到原来的 倍.
A. B. C. D.
11. 把一个圆柱沿底面半径等分后切开,拼接成一个近似的长方体,则
A. 表面积不变,体积变大 B. 表面积增加,体积不变
C. 表面积减少,体积不变 D. 表面积不变,体积变小
12. 两个圆柱形容器内原来的水面高度都是 ,它们的底面直径都是 .①号容器内放入一个小球后,水面高度为 .②号容器内放入一个小球和一个大球后,水面高度为 .两个容器内的小球完全相同,小球的体积与大球的体积的比是
A. B. C. D.
13. 已知一个长方体木块,它的底面是边长为 的正方形,高是 ,把它削成一个最大的圆柱,这个圆柱的体积是
A. B. C. D.
14. 把 个完全相同的小圆柱合成一个大圆柱后,表面积减少了 .已知每个小圆柱的高是 ,每个小圆柱的体积是 .
A. B. C. D.
15. 一满瓶水,喝了一部分后平放在桌面上,剩下部分的高度和喝去部分的高度如图所示.如果把瓶盖拧紧倒置平放,测得无水部分的高度是下面 个数量中的一个数量.那么这个数量最有可能是
A. B. C. D.
四、操作题(共1小题)
16. 求下图的体积.(单位:)
五、解决问题(共5小题)
17. 如下图,这个圆柱的体积是多少立方分米
18. 一个圆柱形油桶装满了汽油,倒出 后还剩 升,油桶的高度是 分米,油桶的底面积是多少平方分米
19. 将一根底面直径是 的圆柱形木料,沿高切成形状,大小完全相同的两块后,表面积增加了 .这根圆柱形木料的体积是多少立方分米
20. 一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置过来放平,无水部分的高是 厘米,内直径是 厘米.小明喝了多少水
21. 在一个圆柱形水桶里,垂直放入一根底面半径为 的圆柱形钢材.如果钢材浸没在水中,桶里的水就上升 ;如果让钢材露出 ,这时桶里的水比钢材浸没在水中时低 .这根钢材的体积是多少立方厘米
答案
一 填空题
1. 底面积,高,,
2. 略
3.
【解析】根据题意,高减少 ,体积就减少 ,在高减少的同时,底面积没有发生变化,减少的体积就是底面积乘减少的高.根据圆柱的体积公式反推,可以得出圆柱的底面积为 .
4.
5. 瓶子里的酸奶的体积;
;
厘米高圆柱的体积;
;
瓶子的容积;
二 判断题
6-9.× √ × √
三 选择题
10. C
11. B
12. A
13. C
14. B
15. B
四 操作题
16. .
,
.
五 解决问题
17. 观察图形可知,圆柱的底面半径是 ,高是 ,利用圆柱的体积公式“”计算即可.
,
答:这个圆柱的体积是 .
18. 平方分米.
19. ,
.
答:这根圆柱形木料的体积是 .由题意可知,圆柱形木料沿高切成形状,大小完全相同的两块后,形成的两个切面为大小一样的两个长方形,所以一个切面的面积为 .长方形切面的相邻两边分别是圆柱的高和底面直径,底面直径已知,由此可求出圆柱的高为 .根据“”可求得圆柱的休积.
20. (立方厘米)
立方厘米 毫升
答:小明喝了 毫升水.
【解析】因为原来的瓶子是装满水的,所以小明喝的水的体积就是倒置后无水部分的体积.根据圆柱的体积公式: 求出空白部分圆柱的体积可得解.
21. ,
,,
答:这根钢材的体积是 .
【解析】由题意可知,露出水面的 的圆柱形钢材的体积为 .而这 长的钢材的体积相当于圆柱形水桶内 高的水的体积.用 可以求出圆柱形水桶的底面积.又知钢材浸没后水面上升 ,可得钢材的体积相当于水桶内 高的水的体积,
第1页(共1 页)
一、填空题(共5小题)
1. 我能观察下图,并填空.
()这个近似长方体的底面积等于圆柱的 ,高等于圆柱的 ,圆柱的体积公式是 .
()图中的圆柱底面半径是 ,高是 ,它的体积是 .
2. 一个圆柱形油桶的底面积是 平方米,高是 米,体积是 立方米.
3. 一个圆柱底面积不变,如果高减少 ,体积就减少 ,那么这个圆柱的底面积是 .
4. 长方形塑料片长 厘米,宽 厘米,按图①截成 片,拼成如图②的无盖的长方体容器(截得的长、宽、高都是整厘米数),这个容器的体积是 立方厘米.
5. 我会分析并解答.
在一个内半径是 的酸奶瓶里,酸奶的高度是 ,把瓶盖拧紧倒置放平,没有酸奶的部分高 .这个瓶子的容积是多少
我先算: ,列式:
再算: ,列式:
最后算: ,列式:
二、判断题(共4小题)
6. 体积相等的两个圆柱一定等底等高.
7. 长方体、正方体、圆柱体的体积都可以用底面积乘以高来计算.
8. 体积是 立方厘米的木块的底面积是 平方厘米.
9. 一个圆柱的高扩大为原来的 倍,底面积缩小为原来的 ,它的体积不变.
三、选择题(共6小题)
10. 若圆柱的底面半径和高都扩大到原来的 倍,则它的体积扩大到原来的 倍.
A. B. C. D.
11. 把一个圆柱沿底面半径等分后切开,拼接成一个近似的长方体,则
A. 表面积不变,体积变大 B. 表面积增加,体积不变
C. 表面积减少,体积不变 D. 表面积不变,体积变小
12. 两个圆柱形容器内原来的水面高度都是 ,它们的底面直径都是 .①号容器内放入一个小球后,水面高度为 .②号容器内放入一个小球和一个大球后,水面高度为 .两个容器内的小球完全相同,小球的体积与大球的体积的比是
A. B. C. D.
13. 已知一个长方体木块,它的底面是边长为 的正方形,高是 ,把它削成一个最大的圆柱,这个圆柱的体积是
A. B. C. D.
14. 把 个完全相同的小圆柱合成一个大圆柱后,表面积减少了 .已知每个小圆柱的高是 ,每个小圆柱的体积是 .
A. B. C. D.
15. 一满瓶水,喝了一部分后平放在桌面上,剩下部分的高度和喝去部分的高度如图所示.如果把瓶盖拧紧倒置平放,测得无水部分的高度是下面 个数量中的一个数量.那么这个数量最有可能是
A. B. C. D.
四、操作题(共1小题)
16. 求下图的体积.(单位:)
五、解决问题(共5小题)
17. 如下图,这个圆柱的体积是多少立方分米
18. 一个圆柱形油桶装满了汽油,倒出 后还剩 升,油桶的高度是 分米,油桶的底面积是多少平方分米
19. 将一根底面直径是 的圆柱形木料,沿高切成形状,大小完全相同的两块后,表面积增加了 .这根圆柱形木料的体积是多少立方分米
20. 一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置过来放平,无水部分的高是 厘米,内直径是 厘米.小明喝了多少水
21. 在一个圆柱形水桶里,垂直放入一根底面半径为 的圆柱形钢材.如果钢材浸没在水中,桶里的水就上升 ;如果让钢材露出 ,这时桶里的水比钢材浸没在水中时低 .这根钢材的体积是多少立方厘米
答案
一 填空题
1. 底面积,高,,
2. 略
3.
【解析】根据题意,高减少 ,体积就减少 ,在高减少的同时,底面积没有发生变化,减少的体积就是底面积乘减少的高.根据圆柱的体积公式反推,可以得出圆柱的底面积为 .
4.
5. 瓶子里的酸奶的体积;
;
厘米高圆柱的体积;
;
瓶子的容积;
二 判断题
6-9.× √ × √
三 选择题
10. C
11. B
12. A
13. C
14. B
15. B
四 操作题
16. .
,
.
五 解决问题
17. 观察图形可知,圆柱的底面半径是 ,高是 ,利用圆柱的体积公式“”计算即可.
,
答:这个圆柱的体积是 .
18. 平方分米.
19. ,
.
答:这根圆柱形木料的体积是 .由题意可知,圆柱形木料沿高切成形状,大小完全相同的两块后,形成的两个切面为大小一样的两个长方形,所以一个切面的面积为 .长方形切面的相邻两边分别是圆柱的高和底面直径,底面直径已知,由此可求出圆柱的高为 .根据“”可求得圆柱的休积.
20. (立方厘米)
立方厘米 毫升
答:小明喝了 毫升水.
【解析】因为原来的瓶子是装满水的,所以小明喝的水的体积就是倒置后无水部分的体积.根据圆柱的体积公式: 求出空白部分圆柱的体积可得解.
21. ,
,,
答:这根钢材的体积是 .
【解析】由题意可知,露出水面的 的圆柱形钢材的体积为 .而这 长的钢材的体积相当于圆柱形水桶内 高的水的体积.用 可以求出圆柱形水桶的底面积.又知钢材浸没后水面上升 ,可得钢材的体积相当于水桶内 高的水的体积,
第1页(共1 页)
