11.1.1 三角形的边 分层作业(含答案) 2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 11.1.1 三角形的边 分层作业(含答案) 2023-2024学年数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 178.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 00:00:00 | ||
图片预览


文档简介
11.1.1 三角形的边
【练基础】
必备知识1 三角形的定义及有关概念
1.下面是小青用三根火柴组成的图形,其中符合三角形概念的是 ( )
A B C D
2.如图,在△ABE中,∠B的对边是 ( )
A.AB B.AD C.AE D.AC
3.如图,以BC为边的三角形是 ,以∠A为一个内角的三角形是 .
必备知识2 三角形的分类
4.【2022·河北期末】下列关于三角形的分类,有如图所示的甲、乙两种分法,则 ( )
A.甲、乙两种分法均正确
B.甲分法正确,乙分法错误
C.甲分法错误,乙分法正确
D.甲、乙两种分法均错误
5.若一个三角形的三边之比是2∶3∶3,周长是24,则这个三角形的最短的边长是 ,按边分,这个三角形是 三角形.
必备知识3 三角形的三边关系
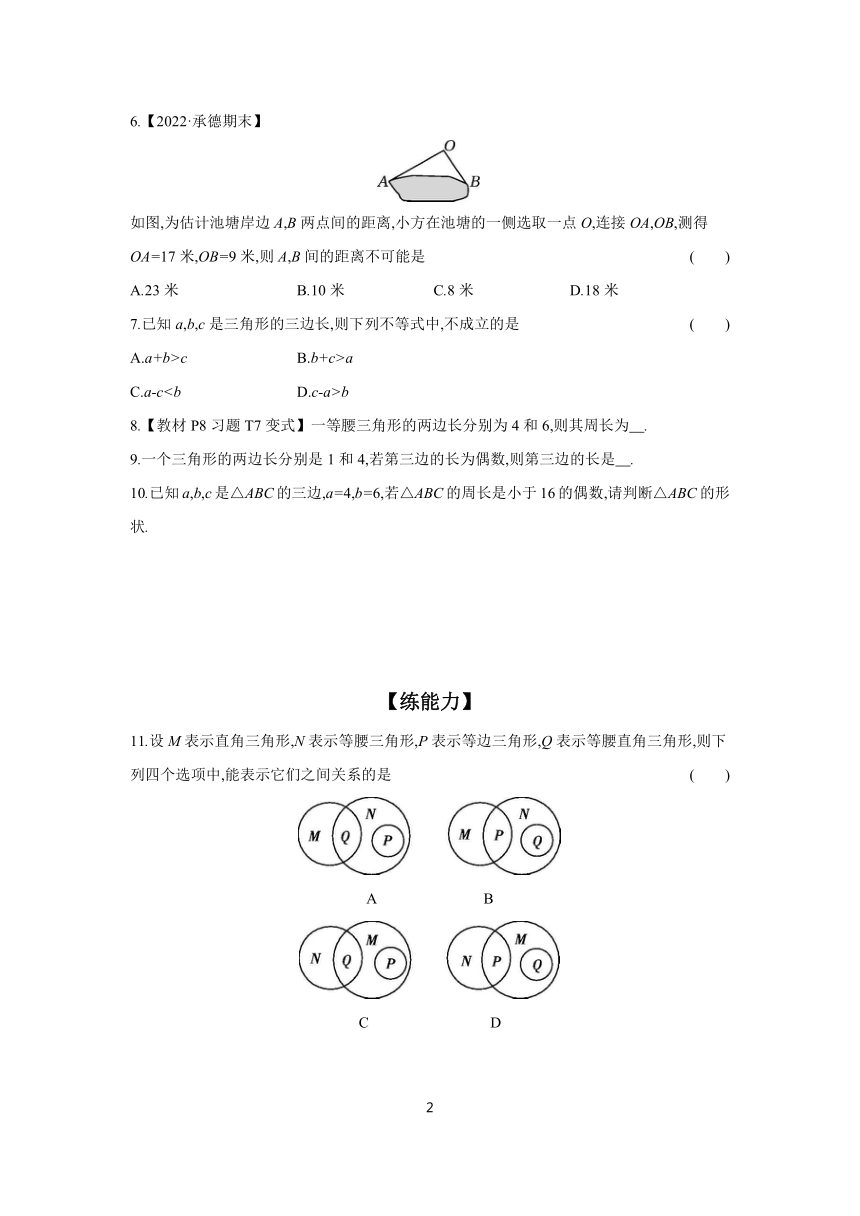
6.【2022·承德期末】
如图,为估计池塘岸边A,B两点间的距离,小方在池塘的一侧选取一点O,连接OA,OB,测得OA=17米,OB=9米,则A,B间的距离不可能是 ( )
A.23米 B.10米 C.8米 D.18米
7.已知a,b,c是三角形的三边长,则下列不等式中,不成立的是 ( )
A.a+b>c B.b+c>a
C.a-cb
8.【教材P8习题T7变式】一等腰三角形的两边长分别为4和6,则其周长为 .
9.一个三角形的两边长分别是1和4,若第三边的长为偶数,则第三边的长是 .
10.已知a,b,c是△ABC的三边,a=4,b=6,若△ABC的周长是小于16的偶数,请判断△ABC的形状.
【练能力】
11.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形,则下列四个选项中,能表示它们之间关系的是 ( )
A B
C D
12.【教材P8习题T2变式】小明有长为2 cm,4 cm,5 cm,7 cm 的四根木条(不能折断),任选其中三根组成三角形,他能组成 个三角形.
13.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以AC为公共边的“共边三角形”有 对.
14.【2022·邯郸月考】如图,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形 个.
15.三个数3,1-a,1-2a在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则a的取值范围为 .
16.如图,小华将一根长度为10 cm的红色小棒分成两段,另再添加一根绿色小棒,使它们可以首尾相接构成一个三角形.若绿色小棒长为a cm(a为正整数),则a的最大值为 .
17.【2022·保定期末】某市木材市场上木棒的规格与价格如下表:
规格 1 m 2 m 3 m 4 m 5 m 6 m
价格/(元/根) 10 15 20 25 30 35
小明的爷爷要做一个三角形的支架,现有两根长度分别为3 m和5 m的木棒,还需要到该木材市场上再购买一根.
(1)有几种规格的木棒可供小明的爷爷选择
(2)在能做成三角形支架的情况下,选择哪一种规格的木棒最省钱
【练素养】
18.如图,D是△ABC内一点.
求证:(1)AB+AC>BD+CD.
(2)AB+BC+AC>AD+BD+CD.
参考答案
练基础
1.B 2.C
3.△ABC,△EBC,△DBC △ABC,△ABE
4.C
5.6 等腰
6.C 7.D
8.14或16
9.4
10.【解析】∵a,b,c是△ABC的三边,a=4,b=6,
∴2∵△ABC的周长是小于16的偶数,
∴2∴c=4.
当c=4时,△ABC的形状是等腰三角形.
练能力
11.A
12.2
13.3
14.21
15.-316.9
【解析】如图,设AB=x cm(x≥5),则AC=(10-x)cm,
由三角形的三边关系得x-(10-x)∴2x-10当a=9时,2x-10<9,
∴x<9.5,
∴a可以取9,即a的最大值为9.
故答案为9.
17.【解析】(1)设第三根木棒的长度为x m.
根据三角形的三边关系可得5-3解得2∴x=3或x=4或x=5或x=6,
∴有4种规格的木棒可供小明的爷爷选择.
(2)根据木棒的价格可得选3 m最省钱.
练素养
18.【解析】证明:(1)如图,延长BD交AC于点E.
在△ABE中,有AB+AE>BE,
在△EDC中,有DE+CE>CD,
∴AB+AE+DE+CE>BE+CD.
∵AE+CE=AC,BE=BD+DE,
∴AB+AC+DE>BD+DE+CD,
∴AB+AC>BD+CD.
(2)由(1)同理可得
AB+BC>AD+CD,
BC+AC>BD+AD,
AB+AC>BD+CD,
∴2(AB+BC+AC)>2(AD+BD+CD),
∴AB+BC+AC>AD+BD+CD.
2
【练基础】
必备知识1 三角形的定义及有关概念
1.下面是小青用三根火柴组成的图形,其中符合三角形概念的是 ( )
A B C D
2.如图,在△ABE中,∠B的对边是 ( )
A.AB B.AD C.AE D.AC
3.如图,以BC为边的三角形是 ,以∠A为一个内角的三角形是 .
必备知识2 三角形的分类
4.【2022·河北期末】下列关于三角形的分类,有如图所示的甲、乙两种分法,则 ( )
A.甲、乙两种分法均正确
B.甲分法正确,乙分法错误
C.甲分法错误,乙分法正确
D.甲、乙两种分法均错误
5.若一个三角形的三边之比是2∶3∶3,周长是24,则这个三角形的最短的边长是 ,按边分,这个三角形是 三角形.
必备知识3 三角形的三边关系
6.【2022·承德期末】
如图,为估计池塘岸边A,B两点间的距离,小方在池塘的一侧选取一点O,连接OA,OB,测得OA=17米,OB=9米,则A,B间的距离不可能是 ( )
A.23米 B.10米 C.8米 D.18米
7.已知a,b,c是三角形的三边长,则下列不等式中,不成立的是 ( )
A.a+b>c B.b+c>a
C.a-c
8.【教材P8习题T7变式】一等腰三角形的两边长分别为4和6,则其周长为 .
9.一个三角形的两边长分别是1和4,若第三边的长为偶数,则第三边的长是 .
10.已知a,b,c是△ABC的三边,a=4,b=6,若△ABC的周长是小于16的偶数,请判断△ABC的形状.
【练能力】
11.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形,则下列四个选项中,能表示它们之间关系的是 ( )
A B
C D
12.【教材P8习题T2变式】小明有长为2 cm,4 cm,5 cm,7 cm 的四根木条(不能折断),任选其中三根组成三角形,他能组成 个三角形.
13.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以AC为公共边的“共边三角形”有 对.
14.【2022·邯郸月考】如图,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形 个.
15.三个数3,1-a,1-2a在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则a的取值范围为 .
16.如图,小华将一根长度为10 cm的红色小棒分成两段,另再添加一根绿色小棒,使它们可以首尾相接构成一个三角形.若绿色小棒长为a cm(a为正整数),则a的最大值为 .
17.【2022·保定期末】某市木材市场上木棒的规格与价格如下表:
规格 1 m 2 m 3 m 4 m 5 m 6 m
价格/(元/根) 10 15 20 25 30 35
小明的爷爷要做一个三角形的支架,现有两根长度分别为3 m和5 m的木棒,还需要到该木材市场上再购买一根.
(1)有几种规格的木棒可供小明的爷爷选择
(2)在能做成三角形支架的情况下,选择哪一种规格的木棒最省钱
【练素养】
18.如图,D是△ABC内一点.
求证:(1)AB+AC>BD+CD.
(2)AB+BC+AC>AD+BD+CD.
参考答案
练基础
1.B 2.C
3.△ABC,△EBC,△DBC △ABC,△ABE
4.C
5.6 等腰
6.C 7.D
8.14或16
9.4
10.【解析】∵a,b,c是△ABC的三边,a=4,b=6,
∴2
∴2
当c=4时,△ABC的形状是等腰三角形.
练能力
11.A
12.2
13.3
14.21
15.-3
【解析】如图,设AB=x cm(x≥5),则AC=(10-x)cm,
由三角形的三边关系得x-(10-x)
∴x<9.5,
∴a可以取9,即a的最大值为9.
故答案为9.
17.【解析】(1)设第三根木棒的长度为x m.
根据三角形的三边关系可得5-3
∴有4种规格的木棒可供小明的爷爷选择.
(2)根据木棒的价格可得选3 m最省钱.
练素养
18.【解析】证明:(1)如图,延长BD交AC于点E.
在△ABE中,有AB+AE>BE,
在△EDC中,有DE+CE>CD,
∴AB+AE+DE+CE>BE+CD.
∵AE+CE=AC,BE=BD+DE,
∴AB+AC+DE>BD+DE+CD,
∴AB+AC>BD+CD.
(2)由(1)同理可得
AB+BC>AD+CD,
BC+AC>BD+AD,
AB+AC>BD+CD,
∴2(AB+BC+AC)>2(AD+BD+CD),
∴AB+BC+AC>AD+BD+CD.
2
