11.2.1 课时1 三角形的内角和 分层作业(含答案) 2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 11.2.1 课时1 三角形的内角和 分层作业(含答案) 2023-2024学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 110.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 21:07:21 | ||
图片预览

文档简介
11.2.1 课时1 三角形的内角和
【练基础】
必备知识 三角形内角和定理
1.下列各组角的度数中,是同一个三角形的内角的度数的是 ( )
A.34°,36°,50° B.63°,70°,67°
C.95°,80°,5° D.25°,160°,15°
2.在△ABC中,∠A=40°,∠B=80°,则∠C的度数是 ( )
A.30° B.40° C.50° D.60°
3.在△ABC中,∠A=x,∠B=2x,∠C=3x,则∠B的度数是 ( )
A.30° B.45° C.50° D.60°
4.如图,∠α的度数是 ( )
A.10° B.20° C.30° D.40°
5.【2022·保定月考】问题:如图,AB,BC被直线AC所截,D是线段AC上的点,过点D作DE∥AB,连接AE,∠B=∠E.求证:AE∥BC.
证法1:∵DE∥AB,∴∠BAE+∠E=180°(※). ∵∠B=∠E,∴∠BAE+∠B=180°, ∴AE∥BC( ). 证法2:∵DE∥AB,∴∠EDA=∠BAC(&). ∵∠B+∠BAC+∠ACB=180°,∠E+∠EAD+∠EDA=180°(三角形内角和等于180°), ∵∠B=∠E,∴∠ACB=∠EAD,∴AE∥BC(◎).
则下列正确的是 ( )
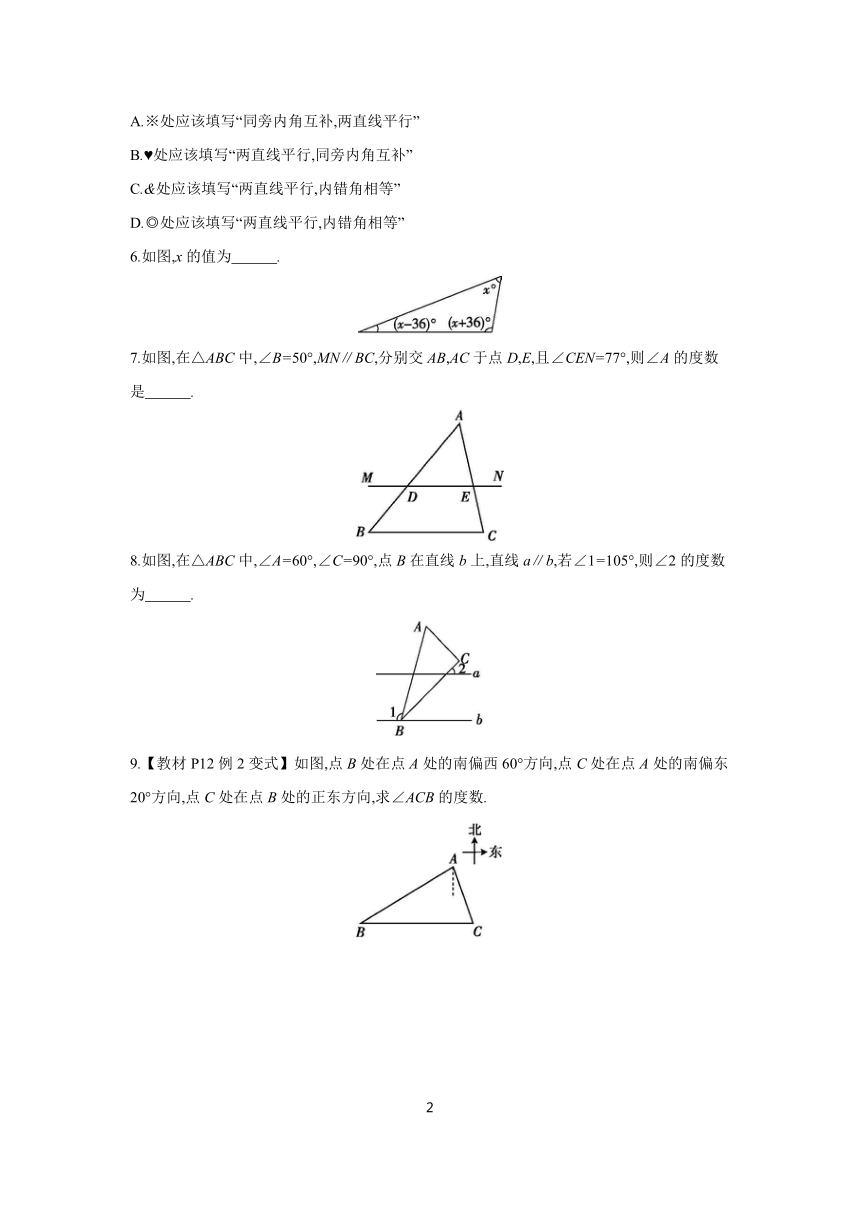
A.※处应该填写“同旁内角互补,两直线平行”
B. 处应该填写“两直线平行,同旁内角互补”
C.&处应该填写“两直线平行,内错角相等”
D.◎处应该填写“两直线平行,内错角相等”
6.如图,x的值为 .
7.如图,在△ABC中,∠B=50°,MN∥BC,分别交AB,AC于点D,E,且∠CEN=77°,则∠A的度数是 .
8.如图,在△ABC中,∠A=60°,∠C=90°,点B在直线b上,直线a∥b,若∠1=105°,则∠2的度数为 .
9.【教材P12例2变式】如图,点B处在点A处的南偏西60°方向,点C处在点A处的南偏东20°方向,点C处在点B处的正东方向,求∠ACB的度数.
【练能力】
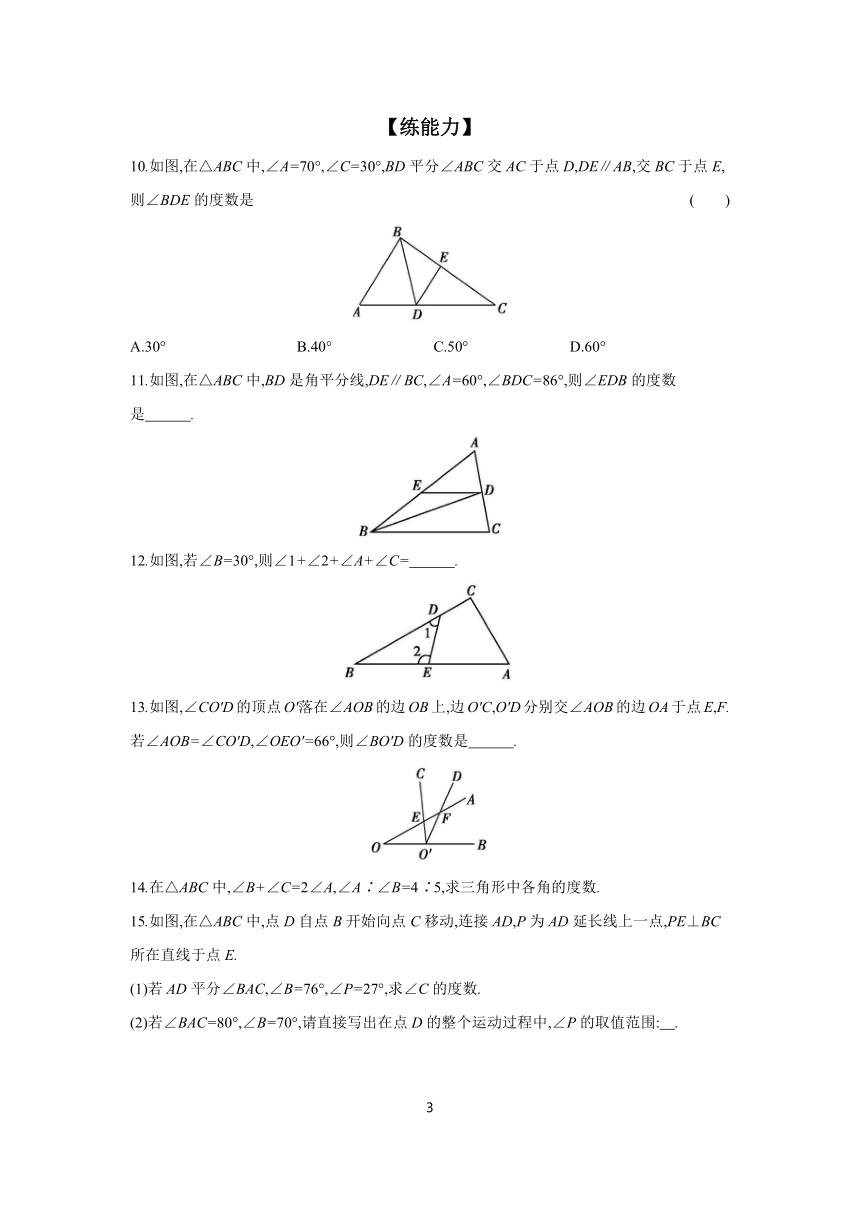
10.如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是 ( )
A.30° B.40° C.50° D.60°
11.如图,在△ABC中,BD是角平分线,DE∥BC,∠A=60°,∠BDC=86°,则∠EDB的度数是 .
12.如图,若∠B=30°,则∠1+∠2+∠A+∠C= .
13.如图,∠CO'D的顶点O'落在∠AOB的边OB上,边O'C,O'D分别交∠AOB的边OA于点E,F.若∠AOB=∠CO'D,∠OEO'=66°,则∠BO'D的度数是 .
14.在△ABC中,∠B+∠C=2∠A,∠A∶∠B=4∶5,求三角形中各角的度数.
15.如图,在△ABC中,点D自点B开始向点C移动,连接AD,P为AD延长线上一点,PE⊥BC所在直线于点E.
(1)若AD平分∠BAC,∠B=76°,∠P=27°,求∠C的度数.
(2)若∠BAC=80°,∠B=70°,请直接写出在点D的整个运动过程中,∠P的取值范围: .
【练素养】
16.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为120°,40°,20°的三角形是“三倍角三角形”.
(1)在△ABC中,∠A=35°,∠B=40°,△ABC是“三倍角三角形”吗 为什么
(2)若△ABC是“三倍角三角形”,且∠B=60°,求△ABC中最小内角的度数.
参考答案
练基础
1.C 2.D 3.D 4.A 5.C
6.60
7.53°
8.45°
9.【解析】∵点B处在点A处的南偏西60°方向,点C处在点A处的南偏东20°方向,点C处在点B处的正东方向,
∴∠ACB=180°-90°-20°=70°.
练能力
10.B
11.26°
12.300°
13.66°
14.【解析】设∠A=4x,∠B=5x,
则∠C=180°-4x-5x=180°-9x.
∵∠B+∠C=2∠A,
∴5x+180°-9x=2×4x,
解得x=15°,
∴∠A=4×15°=60°,∠B=5×15°=75°,∠C=180°-60°-75°=45°.
综上所述,三角形中各角的度数为∠A=60°,∠B=75°,∠C=45°.
15.【解析】(1)∵PE⊥BC,∴∠PEB=90°.
∵∠P=27°,∴∠CDP=180°-90°-27°=63°,
∴∠ADB=∠CDP=63°.
∵∠B=76°,∴∠BAP=180°-∠B-∠ADB=41°.
∵AD平分∠BAC,∴∠BAC=2∠BAP=82°,
∴∠C=180°-∠BAC-∠B=22°.
(2)0°≤∠P≤60°.
提示:∵∠P+∠PDE=90°,
∴只需求∠PDE的范围.
当AD⊥BC时,∠PDE最大为90°,此时D,E两点重合,∠P=0°;
当点D与点C重合时,∠PDE最小,且等于∠ACB=180°-∠B-∠BAC=30°,
此时∠P=90°-∠PDE=60°,
∴∠P的范围是0°≤∠P≤60°.
故答案为0°≤∠P≤60°.
练素养
16.【解析】(1)△ABC是“三倍角三角形”.理由如下:
∵∠A=35°,∠B=40°,
∴∠C=180°-35°-40°=105°=35°×3,
∴△ABC是“三倍角三角形”.
(2)∵∠B=60°,
∴∠A+∠C=120°.
设最小的角为x,
①当60°=3x时,x=20°,
②当x+3x=120°时,x=30°,
∴△ABC中最小内角为20°或30°.
2
【练基础】
必备知识 三角形内角和定理
1.下列各组角的度数中,是同一个三角形的内角的度数的是 ( )
A.34°,36°,50° B.63°,70°,67°
C.95°,80°,5° D.25°,160°,15°
2.在△ABC中,∠A=40°,∠B=80°,则∠C的度数是 ( )
A.30° B.40° C.50° D.60°
3.在△ABC中,∠A=x,∠B=2x,∠C=3x,则∠B的度数是 ( )
A.30° B.45° C.50° D.60°
4.如图,∠α的度数是 ( )
A.10° B.20° C.30° D.40°
5.【2022·保定月考】问题:如图,AB,BC被直线AC所截,D是线段AC上的点,过点D作DE∥AB,连接AE,∠B=∠E.求证:AE∥BC.
证法1:∵DE∥AB,∴∠BAE+∠E=180°(※). ∵∠B=∠E,∴∠BAE+∠B=180°, ∴AE∥BC( ). 证法2:∵DE∥AB,∴∠EDA=∠BAC(&). ∵∠B+∠BAC+∠ACB=180°,∠E+∠EAD+∠EDA=180°(三角形内角和等于180°), ∵∠B=∠E,∴∠ACB=∠EAD,∴AE∥BC(◎).
则下列正确的是 ( )
A.※处应该填写“同旁内角互补,两直线平行”
B. 处应该填写“两直线平行,同旁内角互补”
C.&处应该填写“两直线平行,内错角相等”
D.◎处应该填写“两直线平行,内错角相等”
6.如图,x的值为 .
7.如图,在△ABC中,∠B=50°,MN∥BC,分别交AB,AC于点D,E,且∠CEN=77°,则∠A的度数是 .
8.如图,在△ABC中,∠A=60°,∠C=90°,点B在直线b上,直线a∥b,若∠1=105°,则∠2的度数为 .
9.【教材P12例2变式】如图,点B处在点A处的南偏西60°方向,点C处在点A处的南偏东20°方向,点C处在点B处的正东方向,求∠ACB的度数.
【练能力】
10.如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是 ( )
A.30° B.40° C.50° D.60°
11.如图,在△ABC中,BD是角平分线,DE∥BC,∠A=60°,∠BDC=86°,则∠EDB的度数是 .
12.如图,若∠B=30°,则∠1+∠2+∠A+∠C= .
13.如图,∠CO'D的顶点O'落在∠AOB的边OB上,边O'C,O'D分别交∠AOB的边OA于点E,F.若∠AOB=∠CO'D,∠OEO'=66°,则∠BO'D的度数是 .
14.在△ABC中,∠B+∠C=2∠A,∠A∶∠B=4∶5,求三角形中各角的度数.
15.如图,在△ABC中,点D自点B开始向点C移动,连接AD,P为AD延长线上一点,PE⊥BC所在直线于点E.
(1)若AD平分∠BAC,∠B=76°,∠P=27°,求∠C的度数.
(2)若∠BAC=80°,∠B=70°,请直接写出在点D的整个运动过程中,∠P的取值范围: .
【练素养】
16.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为120°,40°,20°的三角形是“三倍角三角形”.
(1)在△ABC中,∠A=35°,∠B=40°,△ABC是“三倍角三角形”吗 为什么
(2)若△ABC是“三倍角三角形”,且∠B=60°,求△ABC中最小内角的度数.
参考答案
练基础
1.C 2.D 3.D 4.A 5.C
6.60
7.53°
8.45°
9.【解析】∵点B处在点A处的南偏西60°方向,点C处在点A处的南偏东20°方向,点C处在点B处的正东方向,
∴∠ACB=180°-90°-20°=70°.
练能力
10.B
11.26°
12.300°
13.66°
14.【解析】设∠A=4x,∠B=5x,
则∠C=180°-4x-5x=180°-9x.
∵∠B+∠C=2∠A,
∴5x+180°-9x=2×4x,
解得x=15°,
∴∠A=4×15°=60°,∠B=5×15°=75°,∠C=180°-60°-75°=45°.
综上所述,三角形中各角的度数为∠A=60°,∠B=75°,∠C=45°.
15.【解析】(1)∵PE⊥BC,∴∠PEB=90°.
∵∠P=27°,∴∠CDP=180°-90°-27°=63°,
∴∠ADB=∠CDP=63°.
∵∠B=76°,∴∠BAP=180°-∠B-∠ADB=41°.
∵AD平分∠BAC,∴∠BAC=2∠BAP=82°,
∴∠C=180°-∠BAC-∠B=22°.
(2)0°≤∠P≤60°.
提示:∵∠P+∠PDE=90°,
∴只需求∠PDE的范围.
当AD⊥BC时,∠PDE最大为90°,此时D,E两点重合,∠P=0°;
当点D与点C重合时,∠PDE最小,且等于∠ACB=180°-∠B-∠BAC=30°,
此时∠P=90°-∠PDE=60°,
∴∠P的范围是0°≤∠P≤60°.
故答案为0°≤∠P≤60°.
练素养
16.【解析】(1)△ABC是“三倍角三角形”.理由如下:
∵∠A=35°,∠B=40°,
∴∠C=180°-35°-40°=105°=35°×3,
∴△ABC是“三倍角三角形”.
(2)∵∠B=60°,
∴∠A+∠C=120°.
设最小的角为x,
①当60°=3x时,x=20°,
②当x+3x=120°时,x=30°,
∴△ABC中最小内角为20°或30°.
2
