12.2 课时1 边边边(SSS) 分层作业(含答案)2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 12.2 课时1 边边边(SSS) 分层作业(含答案)2023-2024学年数学人教版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 143.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-16 00:00:00 | ||
图片预览


文档简介
12.2 课时1 边边边(SSS)
【练基础】
必备知识1 用“边边边”判定三角形全等
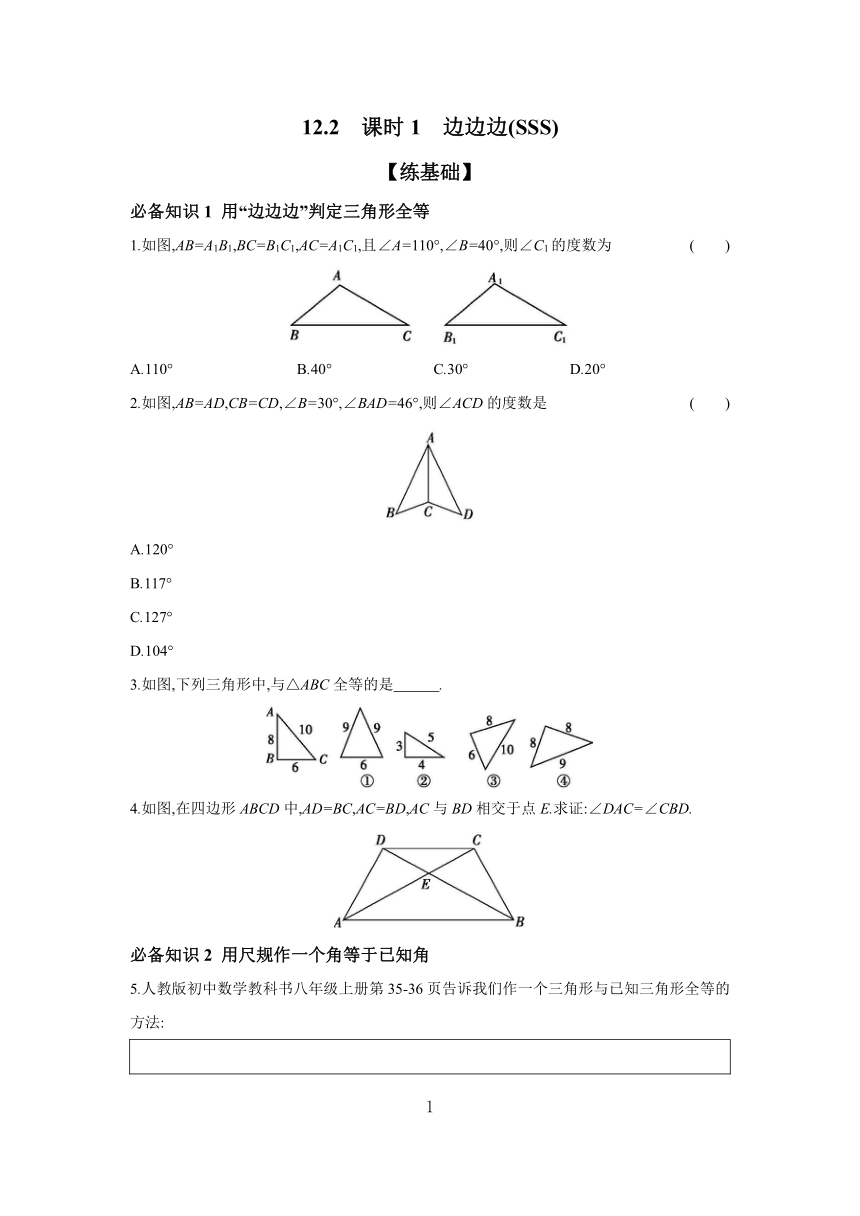
1.如图,AB=A1B1,BC=B1C1,AC=A1C1,且∠A=110°,∠B=40°,则∠C1的度数为 ( )
A.110° B.40° C.30° D.20°
2.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是 ( )
A.120°
B.117°
C.127°
D.104°
3.如图,下列三角形中,与△ABC全等的是 .
4.如图,在四边形ABCD中,AD=BC,AC=BD,AC与BD相交于点E.求证:∠DAC=∠CBD.
必备知识2 用尺规作一个角等于已知角
5.人教版初中数学教科书八年级上册第35-36页告诉我们作一个三角形与已知三角形全等的方法:
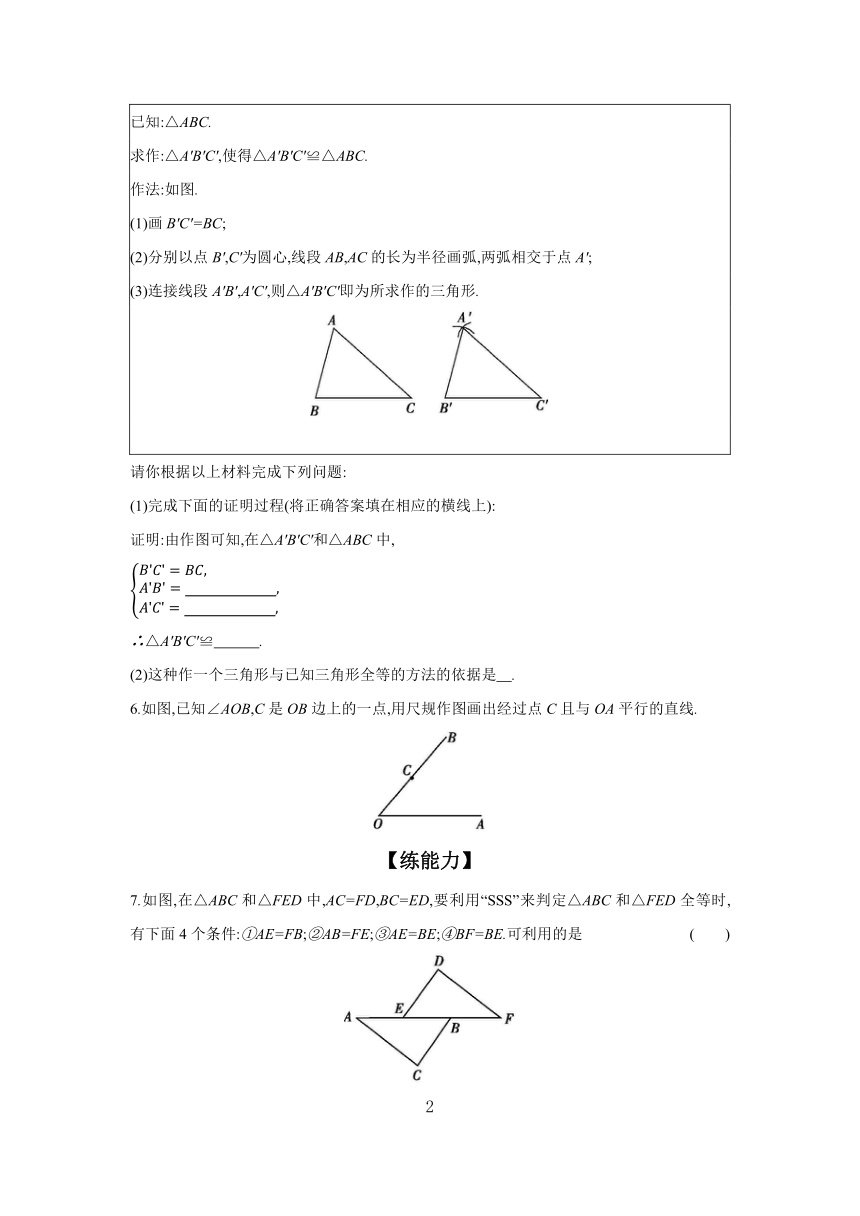
已知:△ABC.
求作:△A'B'C',使得△A'B'C'≌△ABC.
作法:如图.
(1)画B'C'=BC;
(2)分别以点B',C'为圆心,线段AB,AC的长为半径画弧,两弧相交于点A';
(3)连接线段A'B',A'C',则△A'B'C'即为所求作的三角形.
请你根据以上材料完成下列问题:
(1)完成下面的证明过程(将正确答案填在相应的横线上):
证明:由作图可知,在△A'B'C'和△ABC中,
∴△A'B'C'≌ .
(2)这种作一个三角形与已知三角形全等的方法的依据是 .
6.如图,已知∠AOB,C是OB边上的一点,用尺规作图画出经过点C且与OA平行的直线.
【练能力】
7.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,有下面4个条件:①AE=FB;②AB=FE;③AE=BE;④BF=BE.可利用的是 ( )
A.①或② B.②或③ C.①或③ D.①或④
8.已知△ABC的三边长分别为3,5,7,△DEF的三边长分别为3,3x-2,2x-1,若这两个三角形全等,则x等于 ( )
A. B.3 C.4 D.5
9.如图,AB=AC,BD=CD,BH=CH,写出图中所有的全等三角形: .
10.“油纸伞”是我国的传统工艺品之一(如图1),其制作工艺十分巧妙.如图2,伞圈D沿着伞柄AP滑动时,总有伞骨AB=AC,BD=CD.问:伞柄AP是否始终平分同一平面内两条伞骨所成的∠BAC 请说明理由.
11.如图,AB=CB,AD=CD.求证:∠A=∠C.
12.【教材P44习题T9变式】如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:∠A=∠D.
(2)若BF=13,EC=7,求BC的长.
【练素养】
13.如图,AB=AC,AD=AE,BD=CE,求证:∠3=∠1+∠2.
参考答案
练基础
1.C 2.C
3.③
4.【解析】证明:在△CDA和△DCB中,
∴△CDA≌△DCB(SSS),
∴∠DAC=∠CBD.
5.(1)AB AC △ABC
(2)边边边(或SSS)
6.【解析】作图略.提示:以C为顶点,作一个角等于∠AOB.
练能力
7.A 8.B
9.△ABD≌△ACD,△ABH≌△ACH,△BDH≌△CDH
10.【解析】AP始终平分∠BAC.
理由:在△ABD和△ACD中,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴AP始终平分∠BAC.
11.【解析】证明:如图,连接BD.
在△ABD与△CBD中,
∴△ABD≌△CBD(SSS),
∴∠A=∠C.
12.【解析】(1)证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS),
∴∠A=∠D.
(2)∵BE=CF,BF=13,EC=7,
∴BE+CF=BF-EC=6,∴BE=CF=3,
∴BC=BE+EC=3+7=10.
练素养
13.【解析】证明:在△ABD和△ACE中,
∴△ABD≌△ACE(SSS),
∴∠BAD=∠1,∠ABD=∠2.
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
2
【练基础】
必备知识1 用“边边边”判定三角形全等
1.如图,AB=A1B1,BC=B1C1,AC=A1C1,且∠A=110°,∠B=40°,则∠C1的度数为 ( )
A.110° B.40° C.30° D.20°
2.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是 ( )
A.120°
B.117°
C.127°
D.104°
3.如图,下列三角形中,与△ABC全等的是 .
4.如图,在四边形ABCD中,AD=BC,AC=BD,AC与BD相交于点E.求证:∠DAC=∠CBD.
必备知识2 用尺规作一个角等于已知角
5.人教版初中数学教科书八年级上册第35-36页告诉我们作一个三角形与已知三角形全等的方法:
已知:△ABC.
求作:△A'B'C',使得△A'B'C'≌△ABC.
作法:如图.
(1)画B'C'=BC;
(2)分别以点B',C'为圆心,线段AB,AC的长为半径画弧,两弧相交于点A';
(3)连接线段A'B',A'C',则△A'B'C'即为所求作的三角形.
请你根据以上材料完成下列问题:
(1)完成下面的证明过程(将正确答案填在相应的横线上):
证明:由作图可知,在△A'B'C'和△ABC中,
∴△A'B'C'≌ .
(2)这种作一个三角形与已知三角形全等的方法的依据是 .
6.如图,已知∠AOB,C是OB边上的一点,用尺规作图画出经过点C且与OA平行的直线.
【练能力】
7.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,有下面4个条件:①AE=FB;②AB=FE;③AE=BE;④BF=BE.可利用的是 ( )
A.①或② B.②或③ C.①或③ D.①或④
8.已知△ABC的三边长分别为3,5,7,△DEF的三边长分别为3,3x-2,2x-1,若这两个三角形全等,则x等于 ( )
A. B.3 C.4 D.5
9.如图,AB=AC,BD=CD,BH=CH,写出图中所有的全等三角形: .
10.“油纸伞”是我国的传统工艺品之一(如图1),其制作工艺十分巧妙.如图2,伞圈D沿着伞柄AP滑动时,总有伞骨AB=AC,BD=CD.问:伞柄AP是否始终平分同一平面内两条伞骨所成的∠BAC 请说明理由.
11.如图,AB=CB,AD=CD.求证:∠A=∠C.
12.【教材P44习题T9变式】如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:∠A=∠D.
(2)若BF=13,EC=7,求BC的长.
【练素养】
13.如图,AB=AC,AD=AE,BD=CE,求证:∠3=∠1+∠2.
参考答案
练基础
1.C 2.C
3.③
4.【解析】证明:在△CDA和△DCB中,
∴△CDA≌△DCB(SSS),
∴∠DAC=∠CBD.
5.(1)AB AC △ABC
(2)边边边(或SSS)
6.【解析】作图略.提示:以C为顶点,作一个角等于∠AOB.
练能力
7.A 8.B
9.△ABD≌△ACD,△ABH≌△ACH,△BDH≌△CDH
10.【解析】AP始终平分∠BAC.
理由:在△ABD和△ACD中,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴AP始终平分∠BAC.
11.【解析】证明:如图,连接BD.
在△ABD与△CBD中,
∴△ABD≌△CBD(SSS),
∴∠A=∠C.
12.【解析】(1)证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS),
∴∠A=∠D.
(2)∵BE=CF,BF=13,EC=7,
∴BE+CF=BF-EC=6,∴BE=CF=3,
∴BC=BE+EC=3+7=10.
练素养
13.【解析】证明:在△ABD和△ACE中,
∴△ABD≌△ACE(SSS),
∴∠BAD=∠1,∠ABD=∠2.
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
2
