12.2 课时2 边角边(SAS) 分层作业(含答案) 2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 12.2 课时2 边角边(SAS) 分层作业(含答案) 2023-2024学年数学人教版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 125.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-16 00:00:00 | ||
图片预览



文档简介
12.2 课时2 边角边(SAS)
【练基础】
必备知识 用“边角边”判定三角形全等
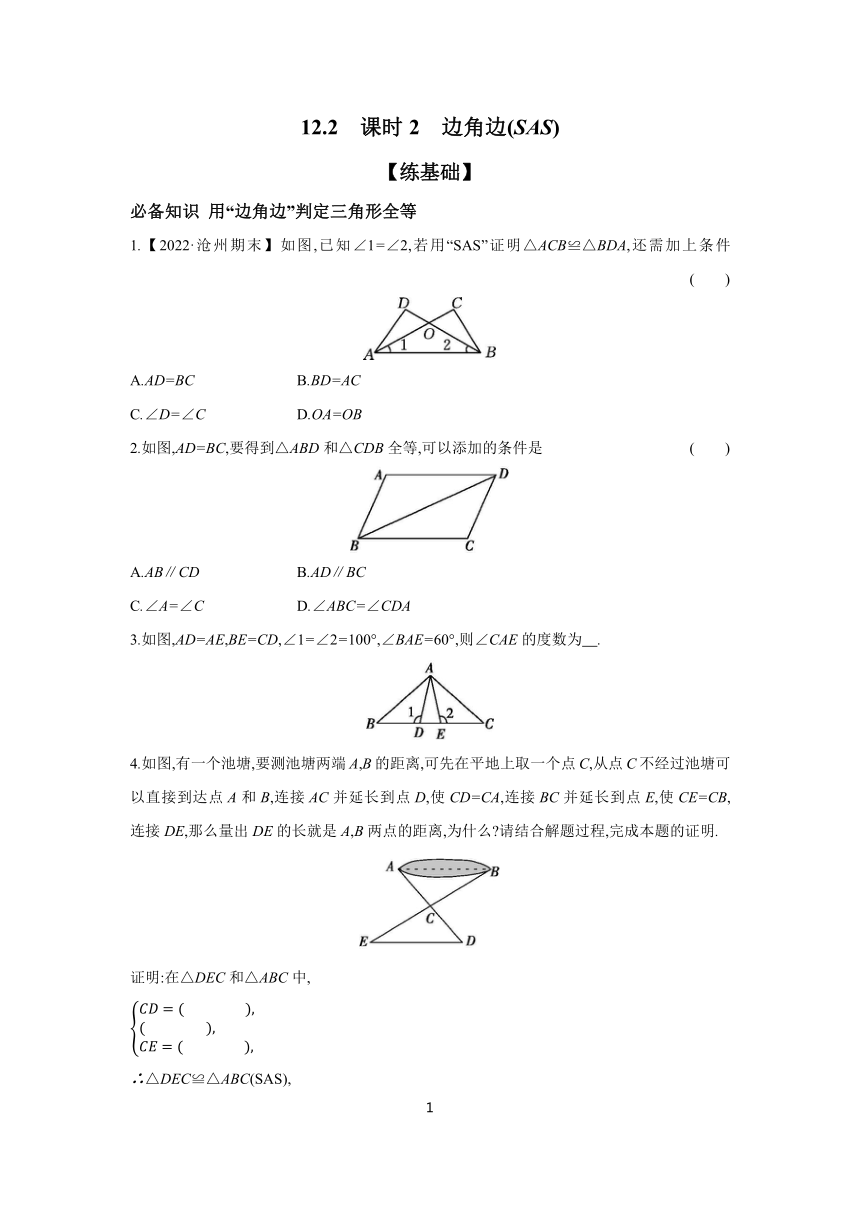
1.【2022·沧州期末】如图,已知∠1=∠2,若用“SAS”证明△ACB≌△BDA,还需加上条件 ( )
A.AD=BC B.BD=AC
C.∠D=∠C D.OA=OB
2.如图,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是 ( )
A.AB∥CD B.AD∥BC
C.∠A=∠C D.∠ABC=∠CDA
3.如图,AD=AE,BE=CD,∠1=∠2=100°,∠BAE=60°,则∠CAE的度数为 .
4.如图,有一个池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE,那么量出DE的长就是A,B两点的距离,为什么 请结合解题过程,完成本题的证明.
证明:在△DEC和△ABC中,
∴△DEC≌△ABC(SAS),
∴ .
5.【2022·邯郸期中】图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=50°,求∠D的大小.
【练能力】
6.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件可以是 ( )
A.∠A=∠D
B.∠E=∠C
C.∠A=∠C
D.∠ABD=∠EBC
7.如图,AC=DE,BC=AE,BC⊥CE,DE⊥CE,垂足分别是C,E,则AB与AD之间的关系是 .
8.【教材P44习题T11变式】如图,点A,F,C,D在同一条直线上,AB∥DE,AB=DE,AF=DC.求证:BC∥EF.
9.如图,已知五边形ABCDE的各边都相等,各内角也都相等,点F,G分别在边BC,CD上,且FC=GD.
(1)求证:△CDF≌△DEG.
(2)求∠EHF的大小.
10.(1)如图1,CE与AB交于点E,AC=BC,∠1=∠2.求证:△ACE≌△BCE.
(2)如图2,CD的延长线与AB交于点E,AD=BC,∠3=∠4,在CE上取CF=DE,连接BF.探究∠BEF与∠EFB的数量关系,并说明理由.
【练素养】
11.如图,在△ABC和△ADE中,AB=AD,∠B=∠D,BC=DE.边AD与边BC交于点P(不与点B,C重合),点B,E在AD异侧.
(1)若∠B=30°,∠APC=70°,求∠CAE的度数.
(2)当AB⊥AC,AB=4,AC=3,BC=5时,设AP=x,请用含x的式子表示PD,并求出PD的最大值.
参考答案
练基础
1.B 2.B
3.40°
4.【解析】证明:在△DEC和△ABC中,
∴△DEC≌△ABC(SAS),
∴DE=AB.
故答案为CA;∠DCE=∠ACB;CB;DE=AB.
5.【解析】∵∠BAD=∠EAC,
∴∠BAD+∠CAD=∠EAC+∠CAD,即∠BAC=∠EAD.
在△BAC与△EAD中,
∴△BAC≌△EAD(SAS),
∴∠D=∠C=50°.
练能力
6.D
7.相等且互相垂直
8.【解析】证明:∵AB∥DE,
∴∠A=∠D.
∵AF=DC,∴AF+FC=DC+CF,即AC=DF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
∴∠ACB=∠DFE,∴BC∥EF.
9.【解析】(1)证明:∵五边形ABCDE的各边都相等,各内角也都相等,
∴CD=DE,∠FCD=∠GDE.
在△CDF和△DEG中,
∴△CDF≌△DEG(SAS).
(2)∵△CDF≌△DEG,
∴∠FDC=∠GED,
∴∠EHF=∠GED+∠HDE
=∠FDC+∠HDE
=∠CDE==108°.
答:∠EHF的大小为108°.
10.【解析】(1)证明:在△ACE和△BCE中,
∴△ACE≌△BCE(SAS).
(2)∠BEF=∠EFB.
理由:在△ADE和△BCF中,
∴△ADE≌△BCF(SAS),
∴∠AED=∠CFB.
∵∠AED+∠BEF=180°,∠CFB+∠EFB=180°,
∴∠BEF=∠EFB.
练素养
11.【解析】(1)在△ABC与△ADE中,
∴△ABC≌△ADE(SAS),
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE.
∵∠B=30°,∠APC=70°,
∴∠CAE=∠BAD=∠APC-∠B=70°-30°=40°.
(2)由(1)得△ABC≌△ADE,∴AB=AD=4.
∵AP=x,∴PD=AD-AP=4-x.
∵AB⊥AC,
∴∠BAC=90°.
∵AB=4,AC=3,BC=5,
∴当AD⊥BC时,x最小,PD最大,PD=4-x,
∴S△ABC=AP·BC=AB·AC,
∴x===2.4,
∴当x最小时,PD有最大值,最大值为4-x=4-2.4=1.6.
2
【练基础】
必备知识 用“边角边”判定三角形全等
1.【2022·沧州期末】如图,已知∠1=∠2,若用“SAS”证明△ACB≌△BDA,还需加上条件 ( )
A.AD=BC B.BD=AC
C.∠D=∠C D.OA=OB
2.如图,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是 ( )
A.AB∥CD B.AD∥BC
C.∠A=∠C D.∠ABC=∠CDA
3.如图,AD=AE,BE=CD,∠1=∠2=100°,∠BAE=60°,则∠CAE的度数为 .
4.如图,有一个池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE,那么量出DE的长就是A,B两点的距离,为什么 请结合解题过程,完成本题的证明.
证明:在△DEC和△ABC中,
∴△DEC≌△ABC(SAS),
∴ .
5.【2022·邯郸期中】图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=50°,求∠D的大小.
【练能力】
6.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件可以是 ( )
A.∠A=∠D
B.∠E=∠C
C.∠A=∠C
D.∠ABD=∠EBC
7.如图,AC=DE,BC=AE,BC⊥CE,DE⊥CE,垂足分别是C,E,则AB与AD之间的关系是 .
8.【教材P44习题T11变式】如图,点A,F,C,D在同一条直线上,AB∥DE,AB=DE,AF=DC.求证:BC∥EF.
9.如图,已知五边形ABCDE的各边都相等,各内角也都相等,点F,G分别在边BC,CD上,且FC=GD.
(1)求证:△CDF≌△DEG.
(2)求∠EHF的大小.
10.(1)如图1,CE与AB交于点E,AC=BC,∠1=∠2.求证:△ACE≌△BCE.
(2)如图2,CD的延长线与AB交于点E,AD=BC,∠3=∠4,在CE上取CF=DE,连接BF.探究∠BEF与∠EFB的数量关系,并说明理由.
【练素养】
11.如图,在△ABC和△ADE中,AB=AD,∠B=∠D,BC=DE.边AD与边BC交于点P(不与点B,C重合),点B,E在AD异侧.
(1)若∠B=30°,∠APC=70°,求∠CAE的度数.
(2)当AB⊥AC,AB=4,AC=3,BC=5时,设AP=x,请用含x的式子表示PD,并求出PD的最大值.
参考答案
练基础
1.B 2.B
3.40°
4.【解析】证明:在△DEC和△ABC中,
∴△DEC≌△ABC(SAS),
∴DE=AB.
故答案为CA;∠DCE=∠ACB;CB;DE=AB.
5.【解析】∵∠BAD=∠EAC,
∴∠BAD+∠CAD=∠EAC+∠CAD,即∠BAC=∠EAD.
在△BAC与△EAD中,
∴△BAC≌△EAD(SAS),
∴∠D=∠C=50°.
练能力
6.D
7.相等且互相垂直
8.【解析】证明:∵AB∥DE,
∴∠A=∠D.
∵AF=DC,∴AF+FC=DC+CF,即AC=DF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
∴∠ACB=∠DFE,∴BC∥EF.
9.【解析】(1)证明:∵五边形ABCDE的各边都相等,各内角也都相等,
∴CD=DE,∠FCD=∠GDE.
在△CDF和△DEG中,
∴△CDF≌△DEG(SAS).
(2)∵△CDF≌△DEG,
∴∠FDC=∠GED,
∴∠EHF=∠GED+∠HDE
=∠FDC+∠HDE
=∠CDE==108°.
答:∠EHF的大小为108°.
10.【解析】(1)证明:在△ACE和△BCE中,
∴△ACE≌△BCE(SAS).
(2)∠BEF=∠EFB.
理由:在△ADE和△BCF中,
∴△ADE≌△BCF(SAS),
∴∠AED=∠CFB.
∵∠AED+∠BEF=180°,∠CFB+∠EFB=180°,
∴∠BEF=∠EFB.
练素养
11.【解析】(1)在△ABC与△ADE中,
∴△ABC≌△ADE(SAS),
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE.
∵∠B=30°,∠APC=70°,
∴∠CAE=∠BAD=∠APC-∠B=70°-30°=40°.
(2)由(1)得△ABC≌△ADE,∴AB=AD=4.
∵AP=x,∴PD=AD-AP=4-x.
∵AB⊥AC,
∴∠BAC=90°.
∵AB=4,AC=3,BC=5,
∴当AD⊥BC时,x最小,PD最大,PD=4-x,
∴S△ABC=AP·BC=AB·AC,
∴x===2.4,
∴当x最小时,PD有最大值,最大值为4-x=4-2.4=1.6.
2
