12.2 课时4 斜边、直角边(HL) 分层作业(含答案) 2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 12.2 课时4 斜边、直角边(HL) 分层作业(含答案) 2023-2024学年数学人教版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 132.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-16 15:40:49 | ||
图片预览

文档简介
12.2 课时4 斜边、直角边(HL)
【练基础】
必备知识 用“斜边、直角边”判定两直角三角形全等
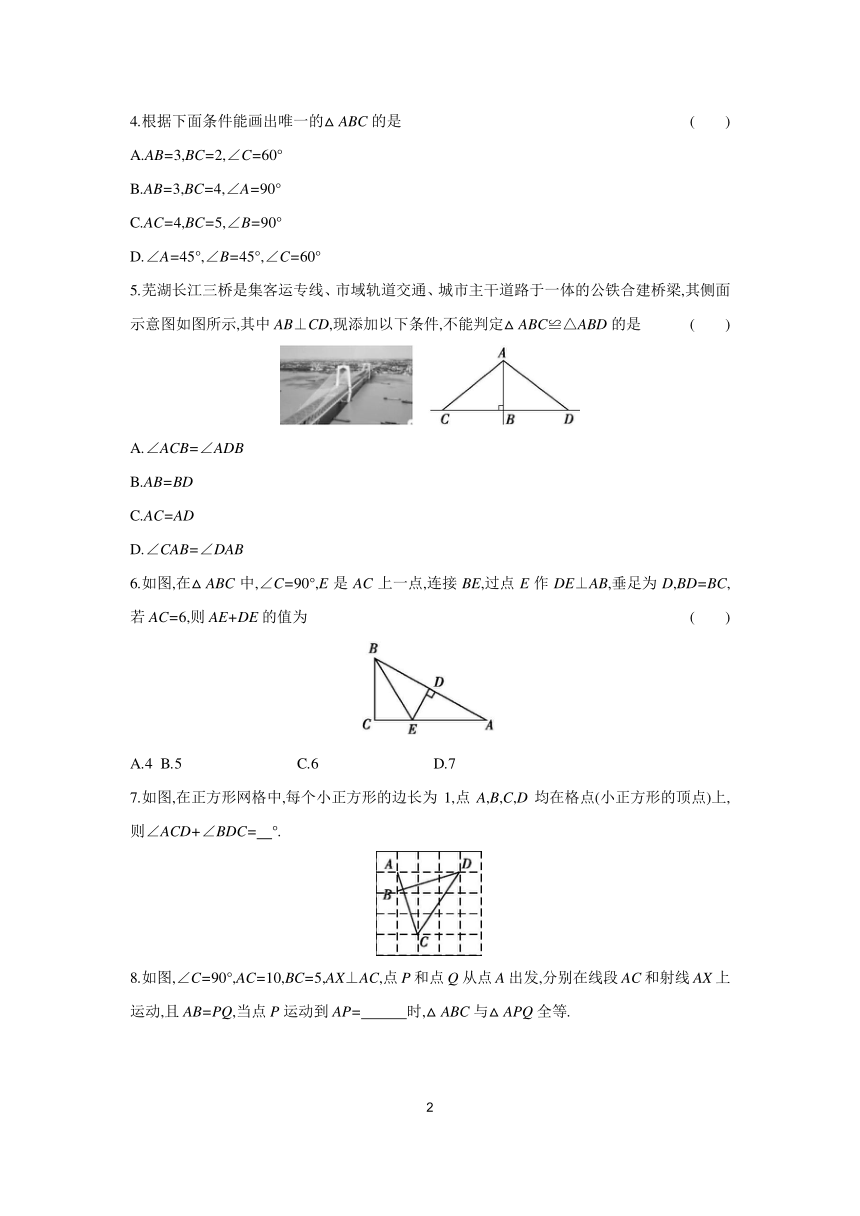
1.【河北期末】如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是 ( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
2.如图,∠B=∠D=90°,BC=CD,若∠1=40°,则∠2的度数为 ( )
A.40°
B.50°
C.60°
D.75°
3.如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:Rt△ABE≌Rt△CBF.
【练能力】
4.根据下面条件能画出唯一的△ABC的是 ( )
A.AB=3,BC=2,∠C=60°
B.AB=3,BC=4,∠A=90°
C.AC=4,BC=5,∠B=90°
D.∠A=45°,∠B=45°,∠C=60°
5.芜湖长江三桥是集客运专线、市域轨道交通、城市主干道路于一体的公铁合建桥梁,其侧面示意图如图所示,其中AB⊥CD,现添加以下条件,不能判定△ABC≌△ABD的是 ( )
A.∠ACB=∠ADB
B.AB=BD
C.AC=AD
D.∠CAB=∠DAB
6.如图,在△ABC中,∠C=90°,E是AC上一点,连接BE,过点E作DE⊥AB,垂足为D,BD=BC,若AC=6,则AE+DE的值为 ( )
A.4 B.5 C.6 D.7
7.如图,在正方形网格中,每个小正方形的边长为1,点A,B,C,D均在格点(小正方形的顶点)上,则∠ACD+∠BDC= °.
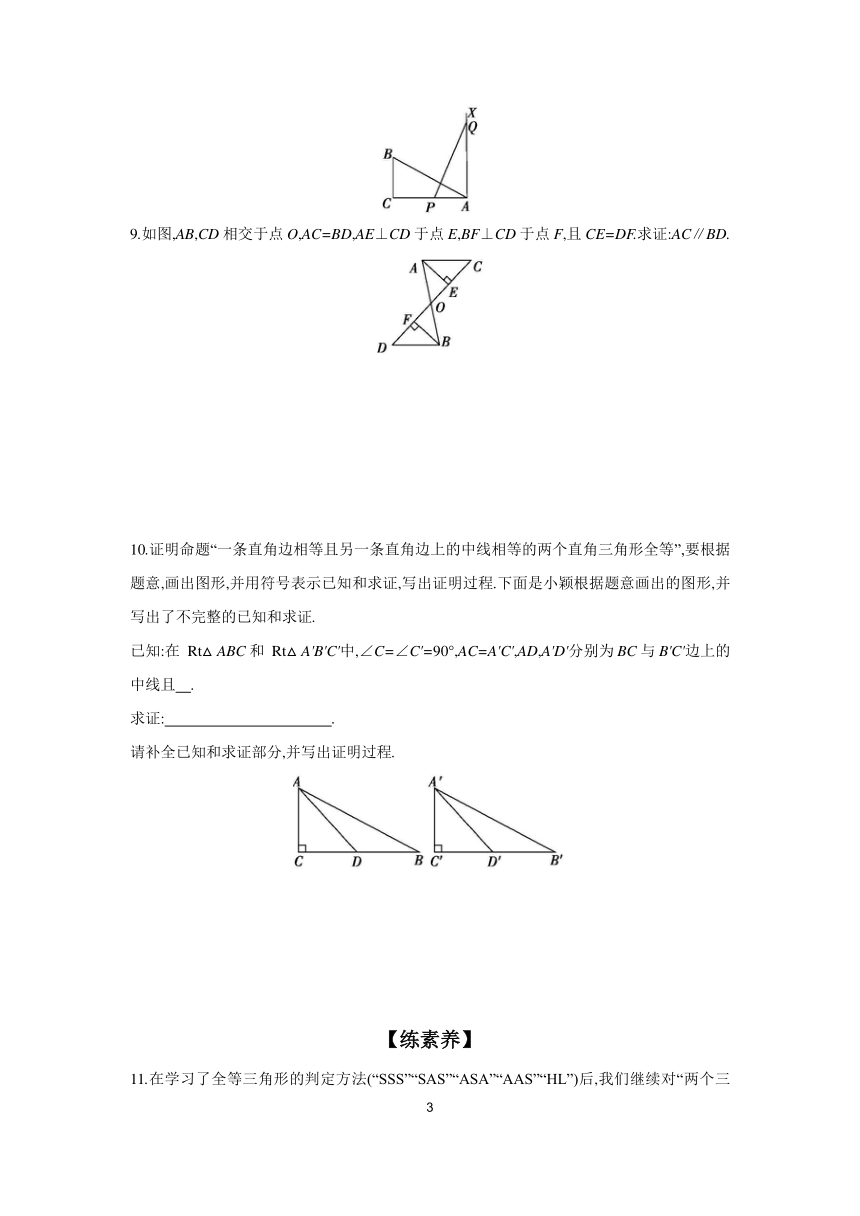
8.如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q从点A出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP= 时,△ABC与△APQ全等.
9.如图,AB,CD相交于点O,AC=BD,AE⊥CD于点E,BF⊥CD于点F,且CE=DF.求证:AC∥BD.
10.证明命题“一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小颖根据题意画出的图形,并写出了不完整的已知和求证.
已知:在 Rt△ABC和 Rt△A'B'C'中,∠C=∠C'=90°,AC=A'C',AD,A'D'分别为BC与B'C'边上的中线且 .
求证: .
请补全已知和求证部分,并写出证明过程.
【练素养】
11.在学习了全等三角形的判定方法(“SSS”“SAS”“ASA”“AAS”“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】将问题用符号语言表示:在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF,然后对∠ABC进行分类,可分为“∠ABC是锐角、直角、钝角”三种情况进行探究.
第一种情况:当∠ABC是锐角时,AB=DE不一定成立.
第二种情况:当∠ABC是直角时,根据“HL”,可得△ABC≌△DEF,则AB=DE.
第三种情况:当∠ABC是钝角时,则AB=DE.
如图,在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF,且∠ABC是钝角.求证:AB=DE.
【方法归纳】化归是一种有效的数学思维方式,一般是将未解决的问题通过变换转化为已解决的问题,观察发现第三种情况可以转化为第二种情况,如图,过点C作CG⊥AB交延长线于点G.
(1)在△DEF中用尺规作出DE边上的高FH,不写作法,保留作图痕迹.
(2)请你在完成(1)中作图的基础上,加以证明AB=DE.
参考答案
练基础
1.A 2.B
3.【解析】证明:∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
练能力
4.B 5.B 6.C
7.90
8.5或10
9.【解析】证明:∵AE⊥CD于点E,BF⊥CD于点F,
∴∠AEC=∠BFD=90°.
在Rt△AEC和Rt△BFD中,
∴Rt△AEC≌Rt△BFD(HL),
∴∠C=∠D,∴AC∥BD.
10.【解析】AD=A'D';Rt△ABC≌Rt△A'B'C'(或△ABC≌△A'B'C').
证明:∵∠C=∠C'=90°,AD=A'D',AC=A'C',
∴Rt△ADC≌Rt△A'D'C'(HL),
∴CD=C'D'.
∵AD与A'D'分别为BC与B'C'边上的中线,
∴D和D'分别是BC和B'C'的中点,
∴BC=2CD,B'C'=2C'D',
∴BC=B'C'.
在△ABC和△A'B'C'中,
∴Rt△ABC≌Rt△A'B'C'(SAS).
练素养
11.【解析】(1)如图,FH即所求.
(2)证明:∵∠ABC=∠DEF,
∴∠CBG=∠FEH.
∵CG⊥AB,FH⊥DE,
∴∠BGC=∠EHF=90°.
∵BC=EF,
∴△CBG≌△FEH(AAS),
∴BG=EH,CG=FH.
∵AC=DF,
∴Rt△ACG≌Rt△DFH(HL),
∴AG=DH,
∴AG-BG=DH-EH,
即AB=DE.
2
【练基础】
必备知识 用“斜边、直角边”判定两直角三角形全等
1.【河北期末】如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是 ( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
2.如图,∠B=∠D=90°,BC=CD,若∠1=40°,则∠2的度数为 ( )
A.40°
B.50°
C.60°
D.75°
3.如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:Rt△ABE≌Rt△CBF.
【练能力】
4.根据下面条件能画出唯一的△ABC的是 ( )
A.AB=3,BC=2,∠C=60°
B.AB=3,BC=4,∠A=90°
C.AC=4,BC=5,∠B=90°
D.∠A=45°,∠B=45°,∠C=60°
5.芜湖长江三桥是集客运专线、市域轨道交通、城市主干道路于一体的公铁合建桥梁,其侧面示意图如图所示,其中AB⊥CD,现添加以下条件,不能判定△ABC≌△ABD的是 ( )
A.∠ACB=∠ADB
B.AB=BD
C.AC=AD
D.∠CAB=∠DAB
6.如图,在△ABC中,∠C=90°,E是AC上一点,连接BE,过点E作DE⊥AB,垂足为D,BD=BC,若AC=6,则AE+DE的值为 ( )
A.4 B.5 C.6 D.7
7.如图,在正方形网格中,每个小正方形的边长为1,点A,B,C,D均在格点(小正方形的顶点)上,则∠ACD+∠BDC= °.
8.如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q从点A出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP= 时,△ABC与△APQ全等.
9.如图,AB,CD相交于点O,AC=BD,AE⊥CD于点E,BF⊥CD于点F,且CE=DF.求证:AC∥BD.
10.证明命题“一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小颖根据题意画出的图形,并写出了不完整的已知和求证.
已知:在 Rt△ABC和 Rt△A'B'C'中,∠C=∠C'=90°,AC=A'C',AD,A'D'分别为BC与B'C'边上的中线且 .
求证: .
请补全已知和求证部分,并写出证明过程.
【练素养】
11.在学习了全等三角形的判定方法(“SSS”“SAS”“ASA”“AAS”“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】将问题用符号语言表示:在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF,然后对∠ABC进行分类,可分为“∠ABC是锐角、直角、钝角”三种情况进行探究.
第一种情况:当∠ABC是锐角时,AB=DE不一定成立.
第二种情况:当∠ABC是直角时,根据“HL”,可得△ABC≌△DEF,则AB=DE.
第三种情况:当∠ABC是钝角时,则AB=DE.
如图,在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF,且∠ABC是钝角.求证:AB=DE.
【方法归纳】化归是一种有效的数学思维方式,一般是将未解决的问题通过变换转化为已解决的问题,观察发现第三种情况可以转化为第二种情况,如图,过点C作CG⊥AB交延长线于点G.
(1)在△DEF中用尺规作出DE边上的高FH,不写作法,保留作图痕迹.
(2)请你在完成(1)中作图的基础上,加以证明AB=DE.
参考答案
练基础
1.A 2.B
3.【解析】证明:∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
练能力
4.B 5.B 6.C
7.90
8.5或10
9.【解析】证明:∵AE⊥CD于点E,BF⊥CD于点F,
∴∠AEC=∠BFD=90°.
在Rt△AEC和Rt△BFD中,
∴Rt△AEC≌Rt△BFD(HL),
∴∠C=∠D,∴AC∥BD.
10.【解析】AD=A'D';Rt△ABC≌Rt△A'B'C'(或△ABC≌△A'B'C').
证明:∵∠C=∠C'=90°,AD=A'D',AC=A'C',
∴Rt△ADC≌Rt△A'D'C'(HL),
∴CD=C'D'.
∵AD与A'D'分别为BC与B'C'边上的中线,
∴D和D'分别是BC和B'C'的中点,
∴BC=2CD,B'C'=2C'D',
∴BC=B'C'.
在△ABC和△A'B'C'中,
∴Rt△ABC≌Rt△A'B'C'(SAS).
练素养
11.【解析】(1)如图,FH即所求.
(2)证明:∵∠ABC=∠DEF,
∴∠CBG=∠FEH.
∵CG⊥AB,FH⊥DE,
∴∠BGC=∠EHF=90°.
∵BC=EF,
∴△CBG≌△FEH(AAS),
∴BG=EH,CG=FH.
∵AC=DF,
∴Rt△ACG≌Rt△DFH(HL),
∴AG=DH,
∴AG-BG=DH-EH,
即AB=DE.
2
