12.2 课时3 角边角(ASA)、角角边(AAS) 分层作业(含答案) 2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 12.2 课时3 角边角(ASA)、角角边(AAS) 分层作业(含答案) 2023-2024学年数学人教版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 136.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-16 00:00:00 | ||
图片预览



文档简介
12.2 课时3 角边角(ASA)、角角边(AAS)
【练基础】
必备知识1 用“角边角”判定三角形全等
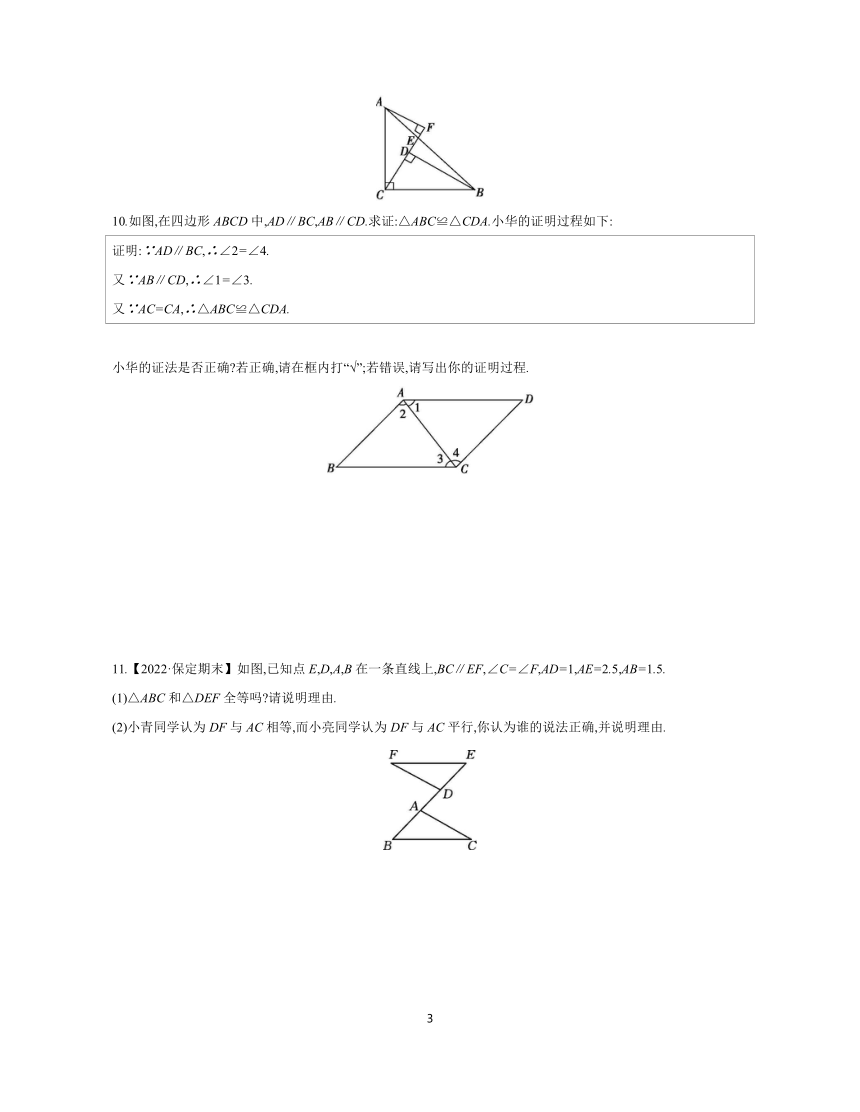
1.如图,AC=DF,∠1=∠2,如果根据“ASA”判定△ABC≌△DEF,那么需要补充的条件是 ( )
A.∠A=∠D B.BF=BG
C.AC=DE D.BA=BD
2.如图,点A,D,C,E在同一条直线上,AB∥EF,AB=EF,AE=14,AC=10,∠B=∠F,则CD的长为 ( )
A.7 B.4 C.4.5 D.6
3.【教材P43习题T2变式】如图,已知AD=AE,能运用“ASA”直接说明△ADC≌△AEB,需添加的条件是 .(不添加任何字母和辅助线)
4.如图,点D,E分别在AB和AC上,AB=AC,∠B=∠C,求证:CE=BD.
必备知识2 用“角角边”判定三角形全等
5.如图,已知AF=CE,BE∥DF,若要用“AAS”证△ABE≌△CDF,则还需添加的一个条件是 .(只要填一个即可)
6.如图,∠A=∠BCD,CA=CD,点E在BC上,且DE∥AB,求证:AB=EC.
【练能力】
7.【2022·唐山期中】如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是 ( )
A.SSS B.SAS
C.AAS D.ASA
8.【河北月考】嘉淇发现有两个结论:在△A1B1C1与△A2B2C2中,①若A1B1=A2B2,A1C1=A2C2,B1C1=B2C2,则△A1B1C1≌△A2B2C2;②若∠A1=∠A2,A1C1=A2C2,B1C1=B2C2,则△A1B1C1≌△A2B2C2.
对于上述的两个结论,下列说法正确的是 ( )
A.①②都错误 B.①②都正确
C.①正确,②错误 D.①错误,②正确
9.【教材P56复习题T9变式】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CF交AB于点E,BD⊥CF于点D,AF⊥CE于点F,现有下列结论:①∠ACF=∠CBD;②BD=FC;③FC=FD+AF;④AE=DC中.其中正确的结论是 .(填正确结论的编号)
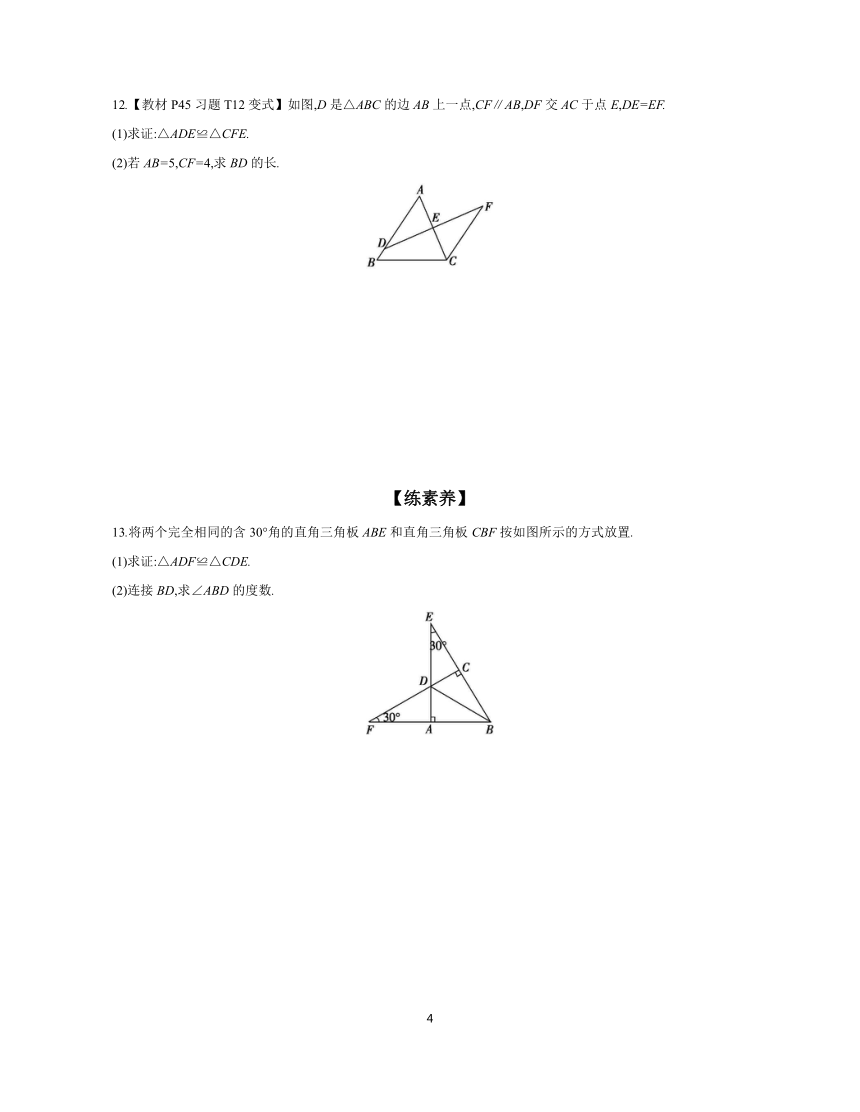
10.如图,在四边形ABCD中,AD∥BC,AB∥CD.求证:△ABC≌△CDA.小华的证明过程如下:
证明:∵AD∥BC,∴∠2=∠4. 又∵AB∥CD,∴∠1=∠3. 又∵AC=CA,∴△ABC≌△CDA.
小华的证法是否正确 若正确,请在框内打“√”;若错误,请写出你的证明过程.
11.【2022·保定期末】如图,已知点E,D,A,B在一条直线上,BC∥EF,∠C=∠F,AD=1,AE=2.5,AB=1.5.
(1)△ABC和△DEF全等吗 请说明理由.
(2)小青同学认为DF与AC相等,而小亮同学认为DF与AC平行,你认为谁的说法正确,并说明理由.
12.【教材P45习题T12变式】如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于点E,DE=EF.
(1)求证:△ADE≌△CFE.
(2)若AB=5,CF=4,求BD的长.
【练素养】
13.将两个完全相同的含30°角的直角三角板ABE和直角三角板CBF按如图所示的方式放置.
(1)求证:△ADF≌△CDE.
(2)连接BD,求∠ABD的度数.
参考答案
练基础
1.A 2.D
3.∠ADC=∠AEB
4.【解析】证明:在△ABE和△ACD中,
∴△ABE≌△ACD(ASA),
∴AE=AD.
又∵AC=AB,
∴CE=BD.
5.∠B=∠D
6.【解析】证明:∵DE∥AB,
∴∠DEC=∠ABC.
在△ABC和△CED中,
∴△ABC≌△CED(AAS),∴AB=EC.
练能力
7.D 8.C
9.①②③
10.【解析】小华的证法不正确.
证明:∵AD∥BC,∴∠1=∠3.
又∵AB∥CD,∴∠2=∠4.
在△ABC和△CDA中,
∴△ABC≌△CDA(ASA).
11.【解析】(1)△ABC≌△DEF.
理由:∵BC∥EF,∴∠B=∠E.
∵AD=1,AE=2.5,
∴DE=AE-AD=2.5-1=1.5.
∵AB=1.5,∴AB=DE.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
(2)两人说的都正确,DF=AC,DF∥AC.
理由:∵△ABC≌△DEF,
∴DF=AC,∠BAC=∠EDF.
∵∠BAC+∠DAC=∠EDF+∠ADF=180°,
∴∠DAC=∠ADF,∴DF∥AC.
12.【解析】(1)证明:∵CF∥AB,
∴∠ADF=∠F,∠A=∠ECF.
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS).
(2)∵△ADE≌△CFE,
∴AD=CF=4,
∴BD=AB-AD=5-4=1.
练素养
13.【解析】(1)证明:根据题意知,Rt△ABE≌Rt△CBF,
∴AB=CB,BE=BF,
∴BE-CB=BF-AB,
∴CE=AF.
在△CDE和△ADF中,
∴△CDE≌△ADF(AAS).
(2)由(1)知,△ADF≌△CDE,∴DE=DF.
在△DFB和△DEB中,
∴△DFB≌△DEB(SAS),
∴∠FBD=∠EBD.
∵∠EBF=60°,∴∠ABD=∠EBF=30°.2
参考答案
练基础
1.A 2.D
3.∠ADC=∠AEB
4.【解析】证明:在△ABE和△ACD中,
∴△ABE≌△ACD(ASA),
∴AE=AD.
又∵AC=AB,
∴CE=BD.
5.∠B=∠D
6.【解析】证明:∵DE∥AB,
∴∠DEC=∠ABC.
在△ABC和△CED中,
∴△ABC≌△CED(AAS),∴AB=EC.
练能力
7.D 8.C
9.①②③
10.【解析】小华的证法不正确.
证明:∵AD∥BC,∴∠1=∠3.
又∵AB∥CD,∴∠2=∠4.
在△ABC和△CDA中,
∴△ABC≌△CDA(ASA).
11.【解析】(1)△ABC≌△DEF.
理由:∵BC∥EF,∴∠B=∠E.
∵AD=1,AE=2.5,
∴DE=AE-AD=2.5-1=1.5.
∵AB=1.5,∴AB=DE.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
(2)两人说的都正确,DF=AC,DF∥AC.
理由:∵△ABC≌△DEF,
∴DF=AC,∠BAC=∠EDF.
∵∠BAC+∠DAC=∠EDF+∠ADF=180°,
∴∠DAC=∠ADF,∴DF∥AC.
12.【解析】(1)证明:∵CF∥AB,
∴∠ADF=∠F,∠A=∠ECF.
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS).
(2)∵△ADE≌△CFE,
∴AD=CF=4,
∴BD=AB-AD=5-4=1.
练素养
13.【解析】(1)证明:根据题意知,Rt△ABE≌Rt△CBF,
∴AB=CB,BE=BF,
∴BE-CB=BF-AB,
∴CE=AF.
在△CDE和△ADF中,
∴△CDE≌△ADF(AAS).
(2)由(1)知,△ADF≌△CDE,∴DE=DF.
在△DFB和△DEB中,
∴△DFB≌△DEB(SAS),
∴∠FBD=∠EBD.
∵∠EBF=60°,∴∠ABD=∠EBF=30°.
2
【练基础】
必备知识1 用“角边角”判定三角形全等
1.如图,AC=DF,∠1=∠2,如果根据“ASA”判定△ABC≌△DEF,那么需要补充的条件是 ( )
A.∠A=∠D B.BF=BG
C.AC=DE D.BA=BD
2.如图,点A,D,C,E在同一条直线上,AB∥EF,AB=EF,AE=14,AC=10,∠B=∠F,则CD的长为 ( )
A.7 B.4 C.4.5 D.6
3.【教材P43习题T2变式】如图,已知AD=AE,能运用“ASA”直接说明△ADC≌△AEB,需添加的条件是 .(不添加任何字母和辅助线)
4.如图,点D,E分别在AB和AC上,AB=AC,∠B=∠C,求证:CE=BD.
必备知识2 用“角角边”判定三角形全等
5.如图,已知AF=CE,BE∥DF,若要用“AAS”证△ABE≌△CDF,则还需添加的一个条件是 .(只要填一个即可)
6.如图,∠A=∠BCD,CA=CD,点E在BC上,且DE∥AB,求证:AB=EC.
【练能力】
7.【2022·唐山期中】如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是 ( )
A.SSS B.SAS
C.AAS D.ASA
8.【河北月考】嘉淇发现有两个结论:在△A1B1C1与△A2B2C2中,①若A1B1=A2B2,A1C1=A2C2,B1C1=B2C2,则△A1B1C1≌△A2B2C2;②若∠A1=∠A2,A1C1=A2C2,B1C1=B2C2,则△A1B1C1≌△A2B2C2.
对于上述的两个结论,下列说法正确的是 ( )
A.①②都错误 B.①②都正确
C.①正确,②错误 D.①错误,②正确
9.【教材P56复习题T9变式】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CF交AB于点E,BD⊥CF于点D,AF⊥CE于点F,现有下列结论:①∠ACF=∠CBD;②BD=FC;③FC=FD+AF;④AE=DC中.其中正确的结论是 .(填正确结论的编号)
10.如图,在四边形ABCD中,AD∥BC,AB∥CD.求证:△ABC≌△CDA.小华的证明过程如下:
证明:∵AD∥BC,∴∠2=∠4. 又∵AB∥CD,∴∠1=∠3. 又∵AC=CA,∴△ABC≌△CDA.
小华的证法是否正确 若正确,请在框内打“√”;若错误,请写出你的证明过程.
11.【2022·保定期末】如图,已知点E,D,A,B在一条直线上,BC∥EF,∠C=∠F,AD=1,AE=2.5,AB=1.5.
(1)△ABC和△DEF全等吗 请说明理由.
(2)小青同学认为DF与AC相等,而小亮同学认为DF与AC平行,你认为谁的说法正确,并说明理由.
12.【教材P45习题T12变式】如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于点E,DE=EF.
(1)求证:△ADE≌△CFE.
(2)若AB=5,CF=4,求BD的长.
【练素养】
13.将两个完全相同的含30°角的直角三角板ABE和直角三角板CBF按如图所示的方式放置.
(1)求证:△ADF≌△CDE.
(2)连接BD,求∠ABD的度数.
参考答案
练基础
1.A 2.D
3.∠ADC=∠AEB
4.【解析】证明:在△ABE和△ACD中,
∴△ABE≌△ACD(ASA),
∴AE=AD.
又∵AC=AB,
∴CE=BD.
5.∠B=∠D
6.【解析】证明:∵DE∥AB,
∴∠DEC=∠ABC.
在△ABC和△CED中,
∴△ABC≌△CED(AAS),∴AB=EC.
练能力
7.D 8.C
9.①②③
10.【解析】小华的证法不正确.
证明:∵AD∥BC,∴∠1=∠3.
又∵AB∥CD,∴∠2=∠4.
在△ABC和△CDA中,
∴△ABC≌△CDA(ASA).
11.【解析】(1)△ABC≌△DEF.
理由:∵BC∥EF,∴∠B=∠E.
∵AD=1,AE=2.5,
∴DE=AE-AD=2.5-1=1.5.
∵AB=1.5,∴AB=DE.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
(2)两人说的都正确,DF=AC,DF∥AC.
理由:∵△ABC≌△DEF,
∴DF=AC,∠BAC=∠EDF.
∵∠BAC+∠DAC=∠EDF+∠ADF=180°,
∴∠DAC=∠ADF,∴DF∥AC.
12.【解析】(1)证明:∵CF∥AB,
∴∠ADF=∠F,∠A=∠ECF.
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS).
(2)∵△ADE≌△CFE,
∴AD=CF=4,
∴BD=AB-AD=5-4=1.
练素养
13.【解析】(1)证明:根据题意知,Rt△ABE≌Rt△CBF,
∴AB=CB,BE=BF,
∴BE-CB=BF-AB,
∴CE=AF.
在△CDE和△ADF中,
∴△CDE≌△ADF(AAS).
(2)由(1)知,△ADF≌△CDE,∴DE=DF.
在△DFB和△DEB中,
∴△DFB≌△DEB(SAS),
∴∠FBD=∠EBD.
∵∠EBF=60°,∴∠ABD=∠EBF=30°.2
参考答案
练基础
1.A 2.D
3.∠ADC=∠AEB
4.【解析】证明:在△ABE和△ACD中,
∴△ABE≌△ACD(ASA),
∴AE=AD.
又∵AC=AB,
∴CE=BD.
5.∠B=∠D
6.【解析】证明:∵DE∥AB,
∴∠DEC=∠ABC.
在△ABC和△CED中,
∴△ABC≌△CED(AAS),∴AB=EC.
练能力
7.D 8.C
9.①②③
10.【解析】小华的证法不正确.
证明:∵AD∥BC,∴∠1=∠3.
又∵AB∥CD,∴∠2=∠4.
在△ABC和△CDA中,
∴△ABC≌△CDA(ASA).
11.【解析】(1)△ABC≌△DEF.
理由:∵BC∥EF,∴∠B=∠E.
∵AD=1,AE=2.5,
∴DE=AE-AD=2.5-1=1.5.
∵AB=1.5,∴AB=DE.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
(2)两人说的都正确,DF=AC,DF∥AC.
理由:∵△ABC≌△DEF,
∴DF=AC,∠BAC=∠EDF.
∵∠BAC+∠DAC=∠EDF+∠ADF=180°,
∴∠DAC=∠ADF,∴DF∥AC.
12.【解析】(1)证明:∵CF∥AB,
∴∠ADF=∠F,∠A=∠ECF.
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS).
(2)∵△ADE≌△CFE,
∴AD=CF=4,
∴BD=AB-AD=5-4=1.
练素养
13.【解析】(1)证明:根据题意知,Rt△ABE≌Rt△CBF,
∴AB=CB,BE=BF,
∴BE-CB=BF-AB,
∴CE=AF.
在△CDE和△ADF中,
∴△CDE≌△ADF(AAS).
(2)由(1)知,△ADF≌△CDE,∴DE=DF.
在△DFB和△DEB中,
∴△DFB≌△DEB(SAS),
∴∠FBD=∠EBD.
∵∠EBF=60°,∴∠ABD=∠EBF=30°.
2
