12.3 课时1 角平分线的性质 分层作业(含答案) 2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 12.3 课时1 角平分线的性质 分层作业(含答案) 2023-2024学年数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 194.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-16 15:39:51 | ||
图片预览


文档简介
12.3 课时1 角平分线的性质
【练基础】
必备知识1 用尺规作已知角的角平分线
1.如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠CMA=25°,则∠C的度数为 ( )
A.100° B.110°
C.120° D.130°
2.如图,在△ABC中,∠A=70°,根据作图痕迹推断∠BOC的度数为 °.
必备知识2 角平分线的性质
3.【2022·唐山月考】下列各图中,OP是∠MON的平分线,点E,F,G分别在射线OM,ON,OP上,则可以解释定理“角的平分线上的点到角的两边的距离相等”的图形是 ( )
A B
C D
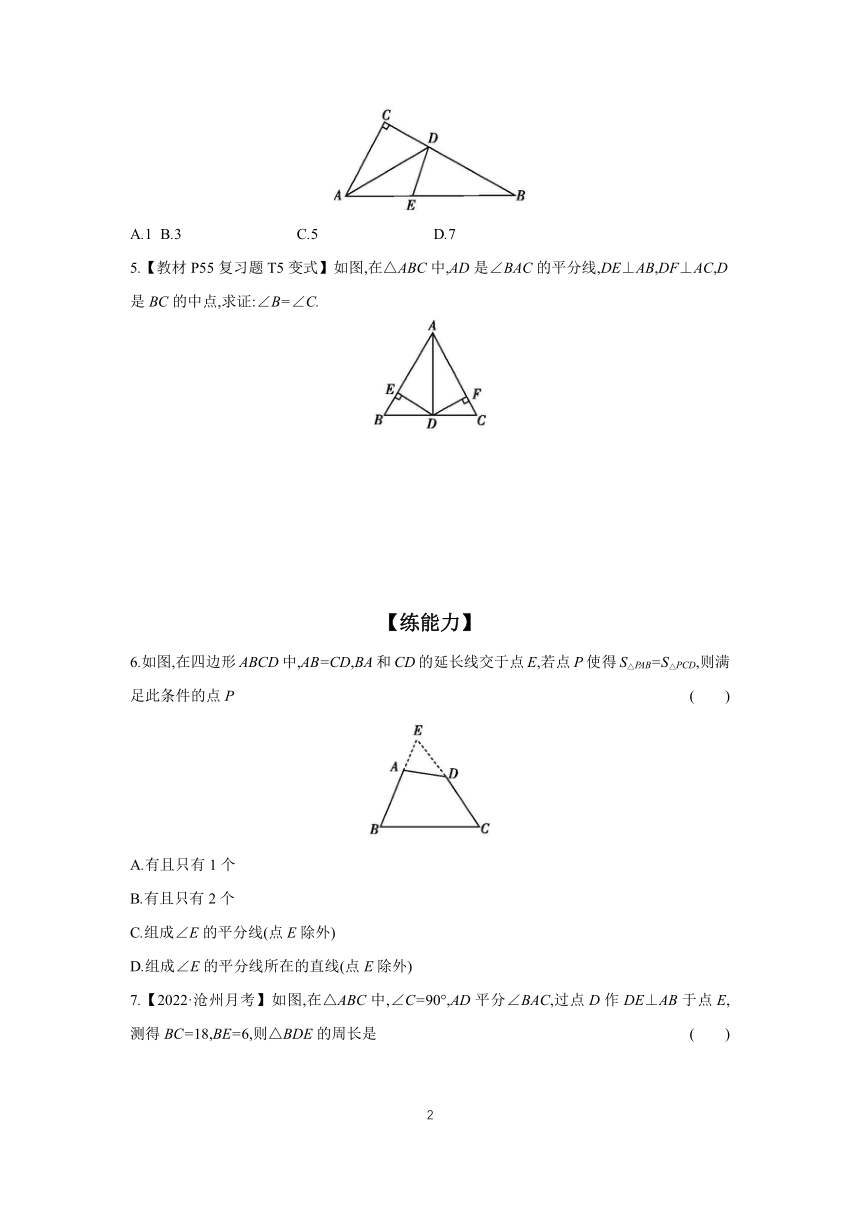
4.【河北期末】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,E是边AB上一点,连接DE,若CD=6,则DE的长可以是 ( )
A.1 B.3 C.5 D.7
5.【教材P55复习题T5变式】如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,D是BC的中点,求证:∠B=∠C.
【练能力】
6.如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P ( )
A.有且只有1个
B.有且只有2个
C.组成∠E的平分线(点E除外)
D.组成∠E的平分线所在的直线(点E除外)
7.【2022·沧州月考】如图,在△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于点E,测得BC=18,BE=6,则△BDE的周长是 ( )
A.30 B.24 C.18 D.12
8.下面是黑板上给出的尺规作图题,需要回答横线上符号代表的内容.
已知∠MAN.
求作:∠MAN的平分线.
作法如下:如图,①以点A为圆心,适当长为半径画弧,交AM于点B,交 于点D;
②分别以点 为圆心,大于 的长为半径画弧,两弧在 的内部交于点C;
③画射线OC,OC即所求.
则下列说法正确的是 ( )
A.○表示AM B. 表示B,C
C.△表示BD D. 表示∠MAN
9.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,∠ACB的平分线与∠ABC的外角平分线交于E点,连接AE,则∠AEB的度数是 ( )
A.30° B.35° C.45° D.35°
10.【教材P52习题T7变式】如图,在四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,若∠CED=35°,则∠EAB的度数是 .
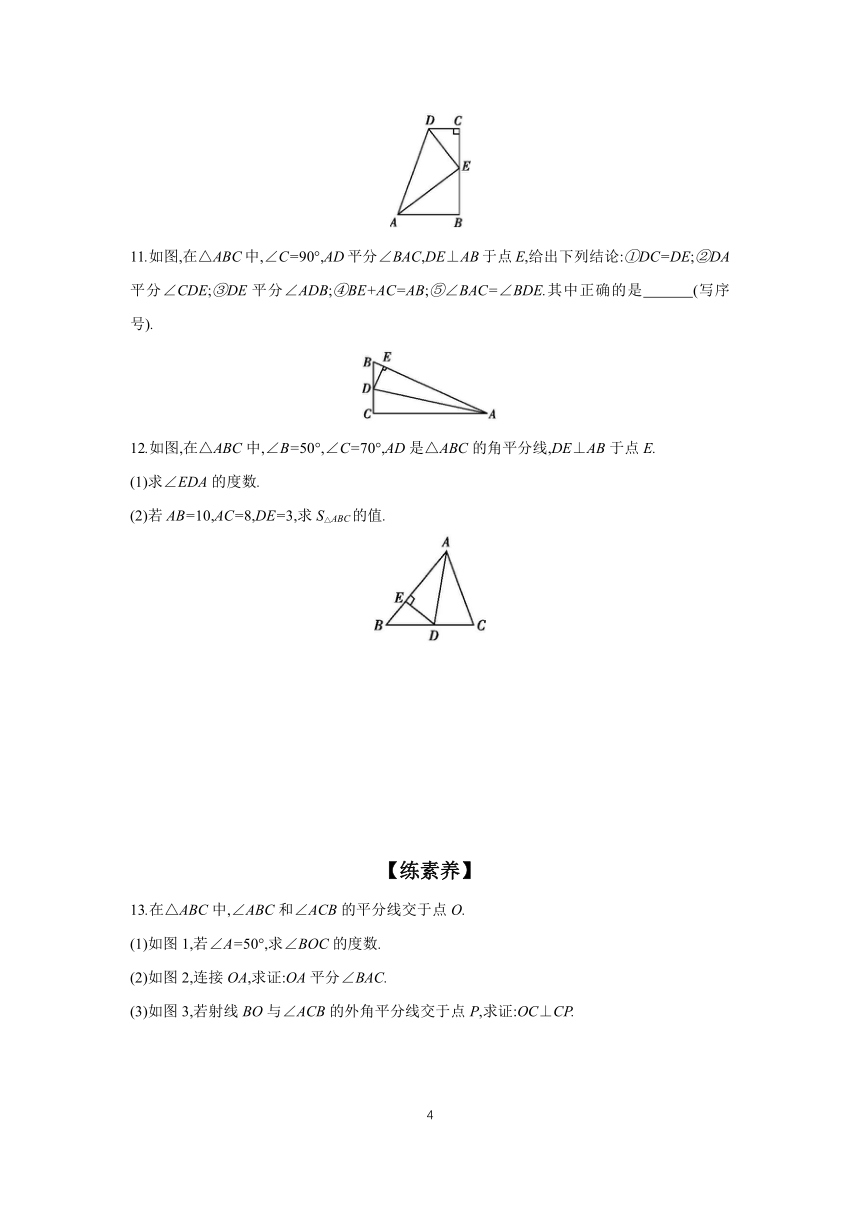
11.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,给出下列结论:①DC=DE;②DA平分∠CDE;③DE平分∠ADB;④BE+AC=AB;⑤∠BAC=∠BDE.其中正确的是 (写序号).
12.如图,在△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于点E.
(1)求∠EDA的度数.
(2)若AB=10,AC=8,DE=3,求S△ABC的值.
【练素养】
13.在△ABC中,∠ABC和∠ACB的平分线交于点O.
(1)如图1,若∠A=50°,求∠BOC的度数.
(2)如图2,连接OA,求证:OA平分∠BAC.
(3)如图3,若射线BO与∠ACB的外角平分线交于点P,求证:OC⊥CP.
参考答案
练基础
1.D
2.125
3.D 4.D
5.【解析】证明:∵D是BC的中点,
∴BD=CD.
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°.
在Rt△BED和Rt△CFD中,
∴Rt△BED≌Rt△CFD(HL),
∴∠B=∠C.
练能力
6.D 7.B 8.D
9.C 【解析】如图,过点E作EF⊥AC交CA的延长线于点F,EG⊥AB于点G,EH⊥BC交CB的延长线于点H.
∵CE平分∠ACB,BE平分∠ABH,
∴EF=EH,EG=EH,
∴EF=EG.又∵EF⊥AC,EG⊥AB,
∴AE平分∠FAG.
∵∠BAC=30°,
∴∠BAF=150°,
∴∠EAB=75°.
∵∠ACB=90°,∠BAC=30°,
∴∠ABC=60°,
∴∠ABH=120°.又∵BE平分∠ABH,
∴∠ABE=60°,
∴∠AEB=180°-∠EAB-∠ABE=45°.
故选C.
10.35°
11.①②④⑤
12.【解析】(1)∵∠B=50°,∠C=70°,
∴∠BAC=180°-∠B-∠C=180°-50°-70°=60°.
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=×60°=30°.
∵DE⊥AB,∴∠DEA=90°,
∴∠EDA=180°-∠BAD-∠DEA=180°-30°-90°=60°.
(2)如图,过点D作DF⊥AC于点F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DF=DE=3.
又∵AB=10,AC=8,
∴S△ABC=×AB×DE+×AC×DF=×10×3+×8×3=27.
练素养
13.【解析】(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°.
∵∠ABC和∠ACB的平分线交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=∠ABC+∠ACB=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=115°.
(2)证明:如图,过点O作OD⊥BC,OE⊥AB,OF⊥AC,垂足分别为D,E,F.
∵∠ABC和∠ACB的平分线交于点O,OD⊥BC,OE⊥AB,OF⊥AC,
∴OD=OE,OD=OF,∴OE=OF.
∵OA=OA,OE=OF,
∴Rt△AOE≌Rt△AOF,
∴∠OAE=∠OAF,
∴OA平分∠BAC.
(3)证明:∵OC平分∠ACB,CP平分∠ACD,
∴∠ACO=∠ACB,∠ACP=∠ACD,
∴∠OCP=∠ACO+∠ACP=∠ACB+∠ACD=∠BCD=×180°=90°,
∴OC⊥CP.
2
【练基础】
必备知识1 用尺规作已知角的角平分线
1.如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠CMA=25°,则∠C的度数为 ( )
A.100° B.110°
C.120° D.130°
2.如图,在△ABC中,∠A=70°,根据作图痕迹推断∠BOC的度数为 °.
必备知识2 角平分线的性质
3.【2022·唐山月考】下列各图中,OP是∠MON的平分线,点E,F,G分别在射线OM,ON,OP上,则可以解释定理“角的平分线上的点到角的两边的距离相等”的图形是 ( )
A B
C D
4.【河北期末】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,E是边AB上一点,连接DE,若CD=6,则DE的长可以是 ( )
A.1 B.3 C.5 D.7
5.【教材P55复习题T5变式】如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,D是BC的中点,求证:∠B=∠C.
【练能力】
6.如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P ( )
A.有且只有1个
B.有且只有2个
C.组成∠E的平分线(点E除外)
D.组成∠E的平分线所在的直线(点E除外)
7.【2022·沧州月考】如图,在△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于点E,测得BC=18,BE=6,则△BDE的周长是 ( )
A.30 B.24 C.18 D.12
8.下面是黑板上给出的尺规作图题,需要回答横线上符号代表的内容.
已知∠MAN.
求作:∠MAN的平分线.
作法如下:如图,①以点A为圆心,适当长为半径画弧,交AM于点B,交 于点D;
②分别以点 为圆心,大于 的长为半径画弧,两弧在 的内部交于点C;
③画射线OC,OC即所求.
则下列说法正确的是 ( )
A.○表示AM B. 表示B,C
C.△表示BD D. 表示∠MAN
9.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,∠ACB的平分线与∠ABC的外角平分线交于E点,连接AE,则∠AEB的度数是 ( )
A.30° B.35° C.45° D.35°
10.【教材P52习题T7变式】如图,在四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,若∠CED=35°,则∠EAB的度数是 .
11.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,给出下列结论:①DC=DE;②DA平分∠CDE;③DE平分∠ADB;④BE+AC=AB;⑤∠BAC=∠BDE.其中正确的是 (写序号).
12.如图,在△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于点E.
(1)求∠EDA的度数.
(2)若AB=10,AC=8,DE=3,求S△ABC的值.
【练素养】
13.在△ABC中,∠ABC和∠ACB的平分线交于点O.
(1)如图1,若∠A=50°,求∠BOC的度数.
(2)如图2,连接OA,求证:OA平分∠BAC.
(3)如图3,若射线BO与∠ACB的外角平分线交于点P,求证:OC⊥CP.
参考答案
练基础
1.D
2.125
3.D 4.D
5.【解析】证明:∵D是BC的中点,
∴BD=CD.
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°.
在Rt△BED和Rt△CFD中,
∴Rt△BED≌Rt△CFD(HL),
∴∠B=∠C.
练能力
6.D 7.B 8.D
9.C 【解析】如图,过点E作EF⊥AC交CA的延长线于点F,EG⊥AB于点G,EH⊥BC交CB的延长线于点H.
∵CE平分∠ACB,BE平分∠ABH,
∴EF=EH,EG=EH,
∴EF=EG.又∵EF⊥AC,EG⊥AB,
∴AE平分∠FAG.
∵∠BAC=30°,
∴∠BAF=150°,
∴∠EAB=75°.
∵∠ACB=90°,∠BAC=30°,
∴∠ABC=60°,
∴∠ABH=120°.又∵BE平分∠ABH,
∴∠ABE=60°,
∴∠AEB=180°-∠EAB-∠ABE=45°.
故选C.
10.35°
11.①②④⑤
12.【解析】(1)∵∠B=50°,∠C=70°,
∴∠BAC=180°-∠B-∠C=180°-50°-70°=60°.
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=×60°=30°.
∵DE⊥AB,∴∠DEA=90°,
∴∠EDA=180°-∠BAD-∠DEA=180°-30°-90°=60°.
(2)如图,过点D作DF⊥AC于点F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DF=DE=3.
又∵AB=10,AC=8,
∴S△ABC=×AB×DE+×AC×DF=×10×3+×8×3=27.
练素养
13.【解析】(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°.
∵∠ABC和∠ACB的平分线交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=∠ABC+∠ACB=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=115°.
(2)证明:如图,过点O作OD⊥BC,OE⊥AB,OF⊥AC,垂足分别为D,E,F.
∵∠ABC和∠ACB的平分线交于点O,OD⊥BC,OE⊥AB,OF⊥AC,
∴OD=OE,OD=OF,∴OE=OF.
∵OA=OA,OE=OF,
∴Rt△AOE≌Rt△AOF,
∴∠OAE=∠OAF,
∴OA平分∠BAC.
(3)证明:∵OC平分∠ACB,CP平分∠ACD,
∴∠ACO=∠ACB,∠ACP=∠ACD,
∴∠OCP=∠ACO+∠ACP=∠ACB+∠ACD=∠BCD=×180°=90°,
∴OC⊥CP.
2
