13.1.2 课时1 线段垂直平分线的性质和判定 分层作业(含答案) 2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 13.1.2 课时1 线段垂直平分线的性质和判定 分层作业(含答案) 2023-2024学年数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 139.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-16 15:38:03 | ||
图片预览

文档简介
13.1.2 课时1 线段垂直平分线的性质和判定
【练基础】
必备知识1 线段垂直平分线的性质
1.如图,在△ABC中,DE垂直平分AC,若BC=6,AD=4,则BD等于 ( )
A.1.5 B.2 C.2.5 D.3
2.【2022·沧州月考】如图,在四边形ABCD中,AC⊥BD,垂足为E,且BE=DE,下列结论不一定成立的是 ( )
A.AB=AD B.AC=BD
C.CA平分∠BCD D.△BEC≌△DEC
3.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,则AB,AC,CE的长度关系为 ( )
A.AB>AC=CE B.AB=AC>CE
C.AB>AC>CE D.AB=AC=CE
4.如图,直线l是线段AB的垂直平分线,C点在直线l外,且与A点在直线l的同一侧,P是直线l上的任意一点,连接AP,BC,CP,则BC与AP+PC的大小关系是 ( )
A.> B.< C.≥ D.≤
5.如图,DE是△ABC的边AB的垂直平分线,分别交AB,BC于点D,E,AE平分∠BAC,若∠B=34°,则∠C的度数为 .
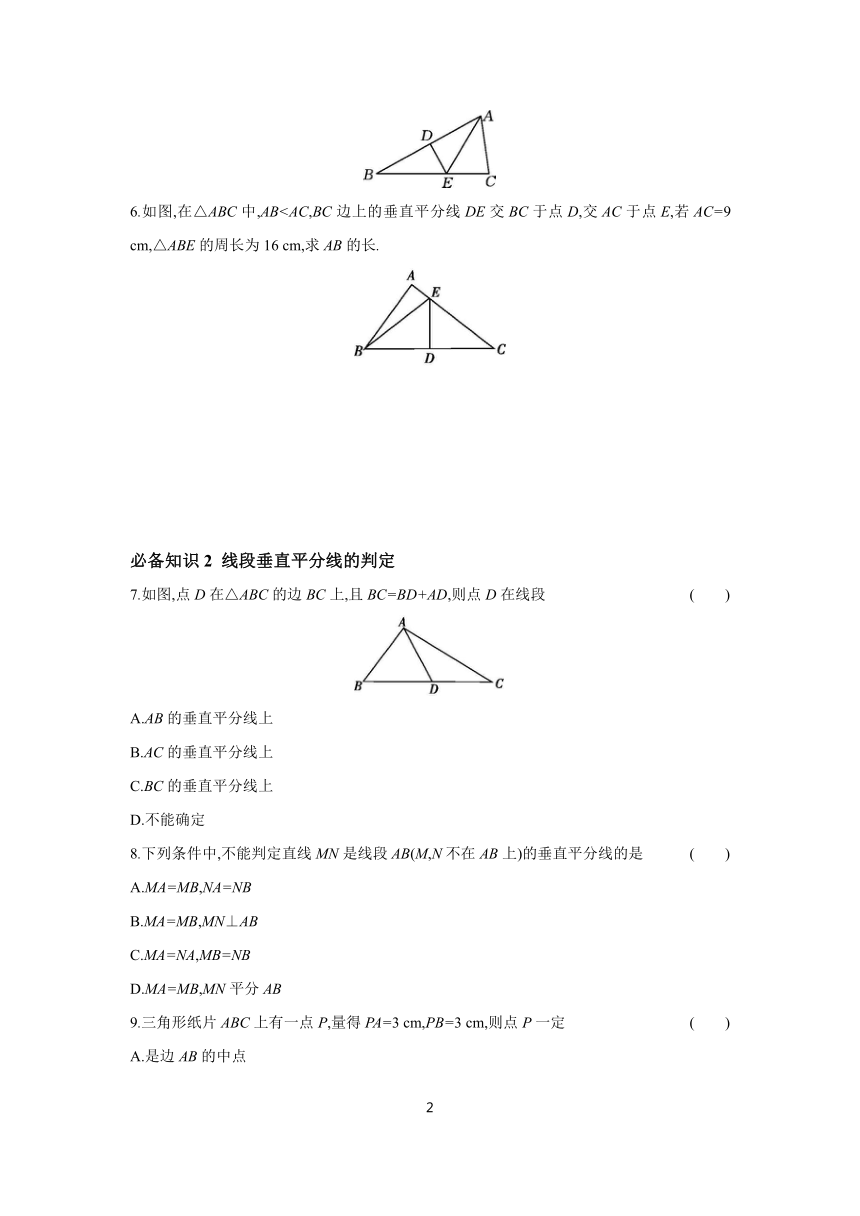
6.如图,在△ABC中,AB必备知识2 线段垂直平分线的判定
7.如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在线段 ( )
A.AB的垂直平分线上
B.AC的垂直平分线上
C.BC的垂直平分线上
D.不能确定
8.下列条件中,不能判定直线MN是线段AB(M,N不在AB上)的垂直平分线的是 ( )
A.MA=MB,NA=NB
B.MA=MB,MN⊥AB
C.MA=NA,MB=NB
D.MA=MB,MN平分AB
9.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定 ( )
A.是边AB的中点
B.在边AB的中线上
C.在边AB的高上
D.在边AB的垂直平分线上
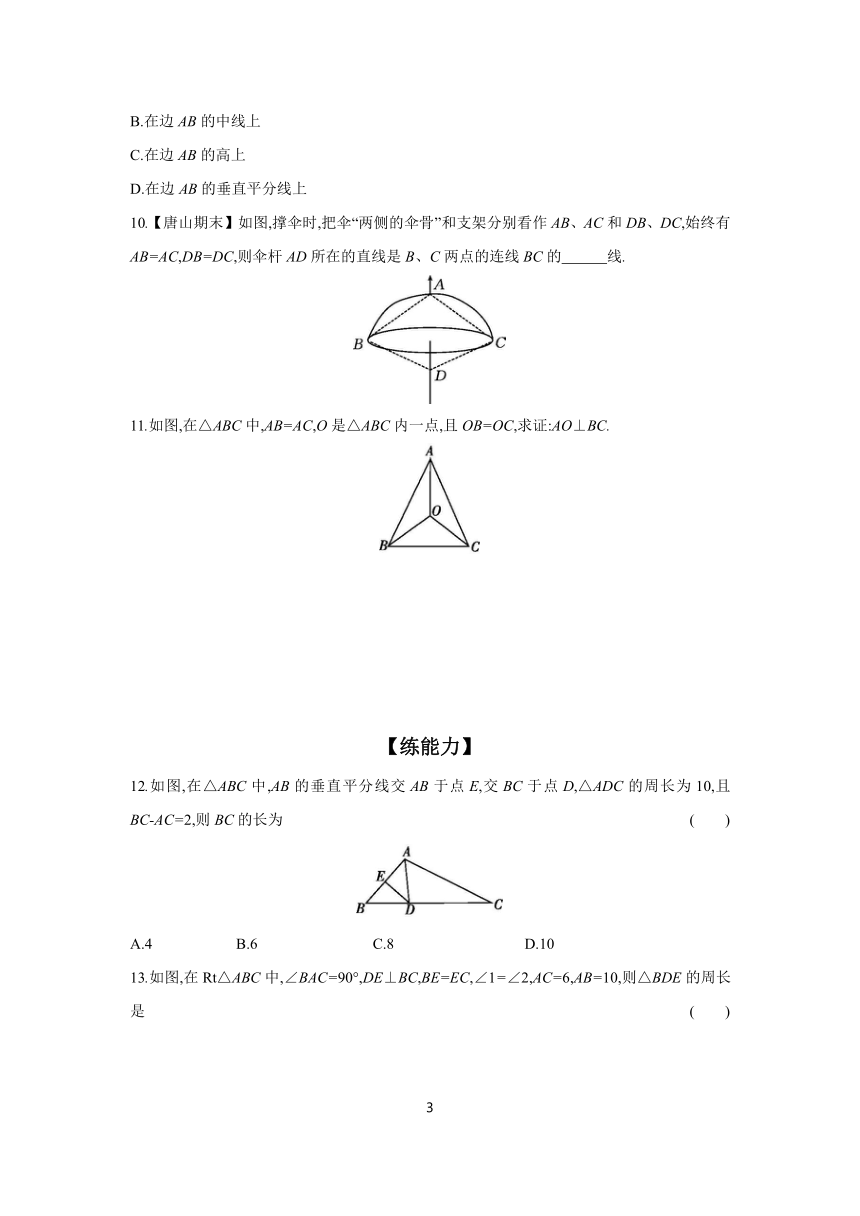
10.【唐山期末】如图,撑伞时,把伞“两侧的伞骨”和支架分别看作AB、AC和DB、DC,始终有AB=AC,DB=DC,则伞杆AD所在的直线是B、C两点的连线BC的 线.
11.如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,求证:AO⊥BC.
【练能力】
12.如图,在△ABC中,AB的垂直平分线交AB于点E,交BC于点D,△ADC的周长为10,且BC-AC=2,则BC的长为 ( )
A.4 B.6 C.8 D.10
13.如图,在Rt△ABC中,∠BAC=90°,DE⊥BC,BE=EC,∠1=∠2,AC=6,AB=10,则△BDE的周长是 ( )
A.15 B.16 C.17 D.18
14.如图,在△ABC中,O是BC,AC的垂直平分线的交点,OB=5 cm,AB=8 cm,则△AOB的周长是 cm.
15.【2022·河北期中】如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,AC的垂直平分线分别交AC,BC于点F,G.
(1)设△AEG的周长为X,当X=12时,求BC的长.
(2)若∠BAC=125°,求∠EAG的度数.
【练素养】
16.如图,BD是△ABC的角平分线.
(1)如图1,DE⊥AB于点E,DF⊥BC于点F,连接EF,求证:BD所在直线是EF的垂直平分线.
(2)如图2,当有一点G从点D向点B运动时,GE⊥AB于点E,GF⊥BC于点F,此时(1)中的结论是否成立 请证明.
(3)如图3,当点G沿BD方向从点D沿BD的延长线运动时,GE⊥AB于点E,GF⊥BC(或其延长线)于点F,此时(1)中的结论是否成立 不需证明.
参考答案
练基础
1.B 2.B 3.D 4.D
5.78°
6.【解析】∵ED是线段BC的垂直平分线,
∴BE=CE,∴BE+AE=CE+AE=AC=9 cm.
∵△ABE的周长为16 cm,
∴AB=16-(BE+AE)=16-9=7 cm.
7.B 8.C 9.D
10.垂直平分
11.【解析】证明:∵AB=AC,
∴点A在BC的垂直平分线上.
∵OB=OC,
∴点O在BC的垂直平分线上,
∴AO垂直平分BC,
∴AO⊥BC.
练能力
12.B 13.B
14.18
15.【解析】(1)∵DE是AB的垂直平分线,GF是AC的垂直平分线,∴EB=EA,GA=GC.
∵BC=BE+EG+GC,∴BC=AE+EG+AG=X=12.
(2)∵∠BAC=125°,∴∠B+∠C=180°-∠BAC=180°-125°=55°.
∵EA=EB,DE=DE,∴Rt△ADE≌Rt△BDE(HL),∴∠BAE=∠B.∵AG=CG,GF=GF,∴Rt△AGF≌Rt△CGF(HL),∴∠GAC=∠C,∴∠EAG=∠BAC-∠BAE-∠GAC=∠BAC-(∠B+∠C)=125°-55°=70°.
练素养
16.【解析】(1)证明:∵BD平分∠ABC,DE⊥AB,DF⊥BC,∴DE=DF,∴点D在EF的垂直平分线上.
在Rt△BDE和Rt△BDF中,∵DE=DF,BD=BD,∴Rt△BDE≌Rt△BDF,∴BE=BF,∴点B在EF的垂直平分线上,∴BD所在直线是EF的垂直平分线.
(2)成立.证明如下:
同(1)可证GE=GF,BE=BF,∴点G,B在EF的垂直平分线上,∴BG所在直线是EF的垂直平分线,即BD所在直线是EF的垂直平分线.
(3)成立.
2
【练基础】
必备知识1 线段垂直平分线的性质
1.如图,在△ABC中,DE垂直平分AC,若BC=6,AD=4,则BD等于 ( )
A.1.5 B.2 C.2.5 D.3
2.【2022·沧州月考】如图,在四边形ABCD中,AC⊥BD,垂足为E,且BE=DE,下列结论不一定成立的是 ( )
A.AB=AD B.AC=BD
C.CA平分∠BCD D.△BEC≌△DEC
3.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,则AB,AC,CE的长度关系为 ( )
A.AB>AC=CE B.AB=AC>CE
C.AB>AC>CE D.AB=AC=CE
4.如图,直线l是线段AB的垂直平分线,C点在直线l外,且与A点在直线l的同一侧,P是直线l上的任意一点,连接AP,BC,CP,则BC与AP+PC的大小关系是 ( )
A.> B.< C.≥ D.≤
5.如图,DE是△ABC的边AB的垂直平分线,分别交AB,BC于点D,E,AE平分∠BAC,若∠B=34°,则∠C的度数为 .
6.如图,在△ABC中,AB
7.如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在线段 ( )
A.AB的垂直平分线上
B.AC的垂直平分线上
C.BC的垂直平分线上
D.不能确定
8.下列条件中,不能判定直线MN是线段AB(M,N不在AB上)的垂直平分线的是 ( )
A.MA=MB,NA=NB
B.MA=MB,MN⊥AB
C.MA=NA,MB=NB
D.MA=MB,MN平分AB
9.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定 ( )
A.是边AB的中点
B.在边AB的中线上
C.在边AB的高上
D.在边AB的垂直平分线上
10.【唐山期末】如图,撑伞时,把伞“两侧的伞骨”和支架分别看作AB、AC和DB、DC,始终有AB=AC,DB=DC,则伞杆AD所在的直线是B、C两点的连线BC的 线.
11.如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,求证:AO⊥BC.
【练能力】
12.如图,在△ABC中,AB的垂直平分线交AB于点E,交BC于点D,△ADC的周长为10,且BC-AC=2,则BC的长为 ( )
A.4 B.6 C.8 D.10
13.如图,在Rt△ABC中,∠BAC=90°,DE⊥BC,BE=EC,∠1=∠2,AC=6,AB=10,则△BDE的周长是 ( )
A.15 B.16 C.17 D.18
14.如图,在△ABC中,O是BC,AC的垂直平分线的交点,OB=5 cm,AB=8 cm,则△AOB的周长是 cm.
15.【2022·河北期中】如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,AC的垂直平分线分别交AC,BC于点F,G.
(1)设△AEG的周长为X,当X=12时,求BC的长.
(2)若∠BAC=125°,求∠EAG的度数.
【练素养】
16.如图,BD是△ABC的角平分线.
(1)如图1,DE⊥AB于点E,DF⊥BC于点F,连接EF,求证:BD所在直线是EF的垂直平分线.
(2)如图2,当有一点G从点D向点B运动时,GE⊥AB于点E,GF⊥BC于点F,此时(1)中的结论是否成立 请证明.
(3)如图3,当点G沿BD方向从点D沿BD的延长线运动时,GE⊥AB于点E,GF⊥BC(或其延长线)于点F,此时(1)中的结论是否成立 不需证明.
参考答案
练基础
1.B 2.B 3.D 4.D
5.78°
6.【解析】∵ED是线段BC的垂直平分线,
∴BE=CE,∴BE+AE=CE+AE=AC=9 cm.
∵△ABE的周长为16 cm,
∴AB=16-(BE+AE)=16-9=7 cm.
7.B 8.C 9.D
10.垂直平分
11.【解析】证明:∵AB=AC,
∴点A在BC的垂直平分线上.
∵OB=OC,
∴点O在BC的垂直平分线上,
∴AO垂直平分BC,
∴AO⊥BC.
练能力
12.B 13.B
14.18
15.【解析】(1)∵DE是AB的垂直平分线,GF是AC的垂直平分线,∴EB=EA,GA=GC.
∵BC=BE+EG+GC,∴BC=AE+EG+AG=X=12.
(2)∵∠BAC=125°,∴∠B+∠C=180°-∠BAC=180°-125°=55°.
∵EA=EB,DE=DE,∴Rt△ADE≌Rt△BDE(HL),∴∠BAE=∠B.∵AG=CG,GF=GF,∴Rt△AGF≌Rt△CGF(HL),∴∠GAC=∠C,∴∠EAG=∠BAC-∠BAE-∠GAC=∠BAC-(∠B+∠C)=125°-55°=70°.
练素养
16.【解析】(1)证明:∵BD平分∠ABC,DE⊥AB,DF⊥BC,∴DE=DF,∴点D在EF的垂直平分线上.
在Rt△BDE和Rt△BDF中,∵DE=DF,BD=BD,∴Rt△BDE≌Rt△BDF,∴BE=BF,∴点B在EF的垂直平分线上,∴BD所在直线是EF的垂直平分线.
(2)成立.证明如下:
同(1)可证GE=GF,BE=BF,∴点G,B在EF的垂直平分线上,∴BG所在直线是EF的垂直平分线,即BD所在直线是EF的垂直平分线.
(3)成立.
2
