13.2 课时2 用坐标表示轴对称 分层作业 (含答案)2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 13.2 课时2 用坐标表示轴对称 分层作业 (含答案)2023-2024学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 313.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 21:57:36 | ||
图片预览


文档简介
13.2 课时2 用坐标表示轴对称
【练基础】
必备知识1 关于坐标轴对称的点的坐标
1.【2022·河北期中】在平面直角坐标系中,点(4,3)关于x轴对称的点的坐标为 ( )
A.(-4,3) B.(-3,4)
C.(4,-3) D.(-4,-3)
2.点A关于y轴的对称点A1坐标是(-2,-1),则点A的坐标是 ( )
A.(-1,-2) B.(2,1)
C.(-2,1) D.(2,-1)
3.在平面直角坐标系中,若点M在第三象限且到x轴的距离为3,到y轴的距离为2,则点M关于x轴对称点N的坐标为 ( )
A.(3,-2) B.(-2,3)
C.(-3,2) D.(-2,-3)
4.已知点P(1-a,a+2)关于y轴的对称点在第二象限,则a的取值范围是 .
5.已知两点的坐标分别是(-2,3)和(2,3),给出下列说法:①两点关于x轴对称;②两点关于y轴对称;③两点之间的距离为4.其中正确的是 .(填序号)
必备知识2 关于坐标轴对称的图形的画法
6.把△ABC各顶点的横坐标都乘以-1,纵坐标都不变,所得图形是下列答案中的 ( )
A B C D
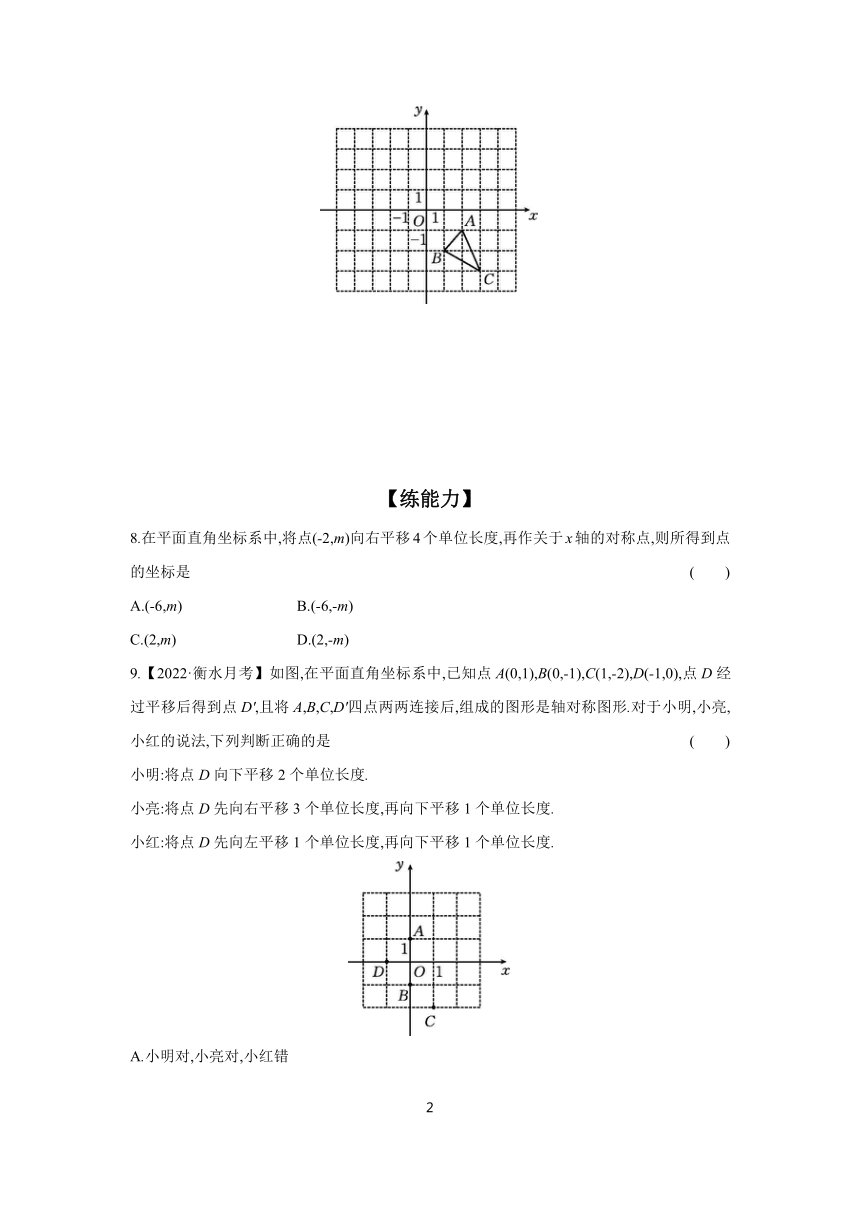
7.【2022·河北期中】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别是A(2,-1),B(1,-2),C(3,-3).
(1)请画出与△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)若点P(m,n)在△ABC的内部,当△ABC沿x轴翻折后,点P对应点P'的坐标是 .
(3)求△ABC的面积.
【练能力】
8.在平面直角坐标系中,将点(-2,m)向右平移4个单位长度,再作关于x轴的对称点,则所得到点的坐标是 ( )
A.(-6,m) B.(-6,-m)
C.(2,m) D.(2,-m)
9.【2022·衡水月考】如图,在平面直角坐标系中,已知点A(0,1),B(0,-1),C(1,-2),D(-1,0),点D经过平移后得到点D',且将A,B,C,D'四点两两连接后,组成的图形是轴对称图形.对于小明,小亮,小红的说法,下列判断正确的是 ( )
小明:将点D向下平移2个单位长度.
小亮:将点D先向右平移3个单位长度,再向下平移1个单位长度.
小红:将点D先向左平移1个单位长度,再向下平移1个单位长度.
A.小明对,小亮对,小红错
B.小明错,小亮对,小红错
C.小明对,小红对,小亮错
D.三个人都对
10.嘉嘉、淇淇两名同学下棋,嘉嘉执圆子,淇淇执方子,如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示,嘉嘉将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,嘉嘉放的位置是 ( )
A.(-2,1)
B.(-1,1)
C.(-1,0)
D.(-1,2)
11.【河北期末】已知点M(a-1,5)和点N(2,b-1)关于y轴对称,则a+b的值为 .
12.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(a,b),则经过第2023次变换后所得的点A坐标是 .
13.已知,在10×10网格中建立下图所示的平面直角坐标系,△ABC是格点三角形(三角形的顶点是网格线的交点).
(1)画出△ABC关于y轴对称的△A1B1C1.
(2)画出△A1B1C1向下平移5个单位长度得到的△A2B2C2.
(3)若点B的坐标为(4,2),请写出点B经过两次图形变换的对应点B2的坐标.
【练素养】
14.如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标.
(2)如果点P的坐标是(-a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.
2
参考答案
练基础
1.C 2.D 3.B
4.-25.②③
6.A
7.【解析】(1)如图所示,△A1B1C1即为所求,
点A1的坐标为(2,1).
(2)(m,-n).
(3)△ABC的面积:2×2-×1×1-×1×2-×1×2=.
练能力
8.D 9.C 10.B
11.5
12.(-a,b)
13.【解析】(1)如图,△A1B1C1即所求.
(2)如图,△A2B2C2即所求.
(3)点B2的坐标为(-4,-3).
练素养
14.【解析】(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2).
(2)如图1,当0∵P与P1关于y轴对称,P(-a,0),∴P1(a,0).又∵P1与P2关于l:直线x=3对称,设P2(x,0),可得=3,即x=6-a,
∴P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.
如图2,当a>3时,
∵P与P1关于y轴对称,P(-a,0),∴P1(a,0).又∵P1与P2关于l:直线x=3对称,设P2(x,0),可得=3,即x=6-a,∴P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.
2
【练基础】
必备知识1 关于坐标轴对称的点的坐标
1.【2022·河北期中】在平面直角坐标系中,点(4,3)关于x轴对称的点的坐标为 ( )
A.(-4,3) B.(-3,4)
C.(4,-3) D.(-4,-3)
2.点A关于y轴的对称点A1坐标是(-2,-1),则点A的坐标是 ( )
A.(-1,-2) B.(2,1)
C.(-2,1) D.(2,-1)
3.在平面直角坐标系中,若点M在第三象限且到x轴的距离为3,到y轴的距离为2,则点M关于x轴对称点N的坐标为 ( )
A.(3,-2) B.(-2,3)
C.(-3,2) D.(-2,-3)
4.已知点P(1-a,a+2)关于y轴的对称点在第二象限,则a的取值范围是 .
5.已知两点的坐标分别是(-2,3)和(2,3),给出下列说法:①两点关于x轴对称;②两点关于y轴对称;③两点之间的距离为4.其中正确的是 .(填序号)
必备知识2 关于坐标轴对称的图形的画法
6.把△ABC各顶点的横坐标都乘以-1,纵坐标都不变,所得图形是下列答案中的 ( )
A B C D
7.【2022·河北期中】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别是A(2,-1),B(1,-2),C(3,-3).
(1)请画出与△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)若点P(m,n)在△ABC的内部,当△ABC沿x轴翻折后,点P对应点P'的坐标是 .
(3)求△ABC的面积.
【练能力】
8.在平面直角坐标系中,将点(-2,m)向右平移4个单位长度,再作关于x轴的对称点,则所得到点的坐标是 ( )
A.(-6,m) B.(-6,-m)
C.(2,m) D.(2,-m)
9.【2022·衡水月考】如图,在平面直角坐标系中,已知点A(0,1),B(0,-1),C(1,-2),D(-1,0),点D经过平移后得到点D',且将A,B,C,D'四点两两连接后,组成的图形是轴对称图形.对于小明,小亮,小红的说法,下列判断正确的是 ( )
小明:将点D向下平移2个单位长度.
小亮:将点D先向右平移3个单位长度,再向下平移1个单位长度.
小红:将点D先向左平移1个单位长度,再向下平移1个单位长度.
A.小明对,小亮对,小红错
B.小明错,小亮对,小红错
C.小明对,小红对,小亮错
D.三个人都对
10.嘉嘉、淇淇两名同学下棋,嘉嘉执圆子,淇淇执方子,如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示,嘉嘉将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,嘉嘉放的位置是 ( )
A.(-2,1)
B.(-1,1)
C.(-1,0)
D.(-1,2)
11.【河北期末】已知点M(a-1,5)和点N(2,b-1)关于y轴对称,则a+b的值为 .
12.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(a,b),则经过第2023次变换后所得的点A坐标是 .
13.已知,在10×10网格中建立下图所示的平面直角坐标系,△ABC是格点三角形(三角形的顶点是网格线的交点).
(1)画出△ABC关于y轴对称的△A1B1C1.
(2)画出△A1B1C1向下平移5个单位长度得到的△A2B2C2.
(3)若点B的坐标为(4,2),请写出点B经过两次图形变换的对应点B2的坐标.
【练素养】
14.如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标.
(2)如果点P的坐标是(-a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.
2
参考答案
练基础
1.C 2.D 3.B
4.-2
6.A
7.【解析】(1)如图所示,△A1B1C1即为所求,
点A1的坐标为(2,1).
(2)(m,-n).
(3)△ABC的面积:2×2-×1×1-×1×2-×1×2=.
练能力
8.D 9.C 10.B
11.5
12.(-a,b)
13.【解析】(1)如图,△A1B1C1即所求.
(2)如图,△A2B2C2即所求.
(3)点B2的坐标为(-4,-3).
练素养
14.【解析】(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2).
(2)如图1,当0
∴P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.
如图2,当a>3时,
∵P与P1关于y轴对称,P(-a,0),∴P1(a,0).又∵P1与P2关于l:直线x=3对称,设P2(x,0),可得=3,即x=6-a,∴P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.
2
