13.3.1 课时1 等腰三角形的性质 分层作业 (含答案)2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 13.3.1 课时1 等腰三角形的性质 分层作业 (含答案)2023-2024学年数学人教版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 141.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 21:57:20 | ||
图片预览


文档简介
13.3.1 课时1 等腰三角形的性质
【练基础】
必备知识1 等边对等角
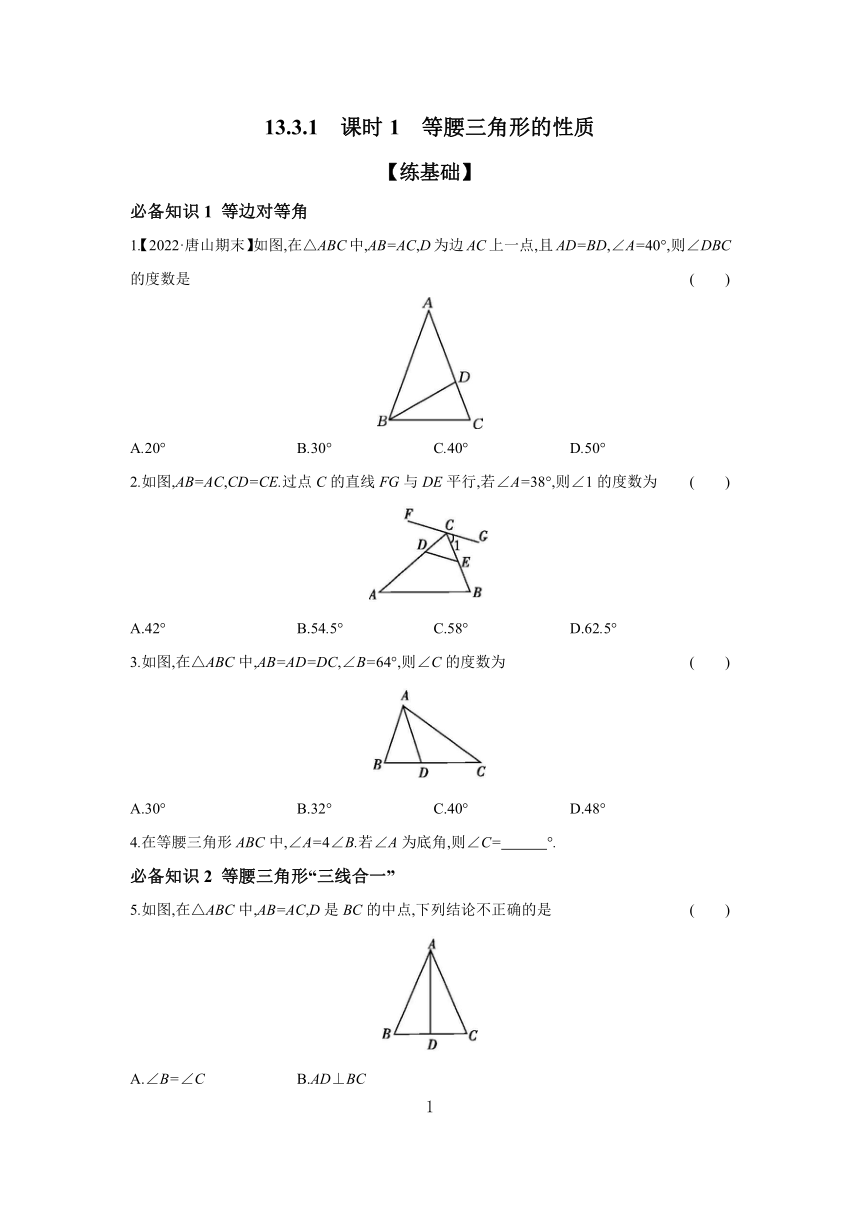
1.【2022·唐山期末】如图,在△ABC中,AB=AC,D为边AC上一点,且AD=BD,∠A=40°,则∠DBC的度数是 ( )
A.20° B.30° C.40° D.50°
2.如图,AB=AC,CD=CE.过点C的直线FG与DE平行,若∠A=38°,则∠1的度数为 ( )
A.42° B.54.5° C.58° D.62.5°
3.如图,在△ABC中,AB=AD=DC,∠B=64°,则∠C的度数为 ( )
A.30° B.32° C.40° D.48°
4.在等腰三角形ABC中,∠A=4∠B.若∠A为底角,则∠C= °.
必备知识2 等腰三角形“三线合一”
5.如图,在△ABC中,AB=AC,D是BC的中点,下列结论不正确的是 ( )
A.∠B=∠C B.AD⊥BC
C.AD平分∠BAC D.AB=2BD
6.如图,BE⊥AC于点D,且AB=BC,BD=ED,若∠ABC=54°,则∠E的大小为 ( )
A.27° B.36° C.40° D.54°
7.如图,在△ABC中,AB=AC.AD是BC边上的中线,点E在边AB上,且BD=BE.若∠BAC=100°,则∠ADE的大小为 .
【练能力】
8.在等腰△ABC中,∠A=70°,则∠C的度数不可能是 ( )
A.40° B.55° C.65° D.70°
9.如图,在△ABC中,AB=AC,以点B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则下列结论不一定成立的是 ( )
A.BC=BD
B.∠BDC=∠ABC
C.∠A=∠CBD
D.AD=BD
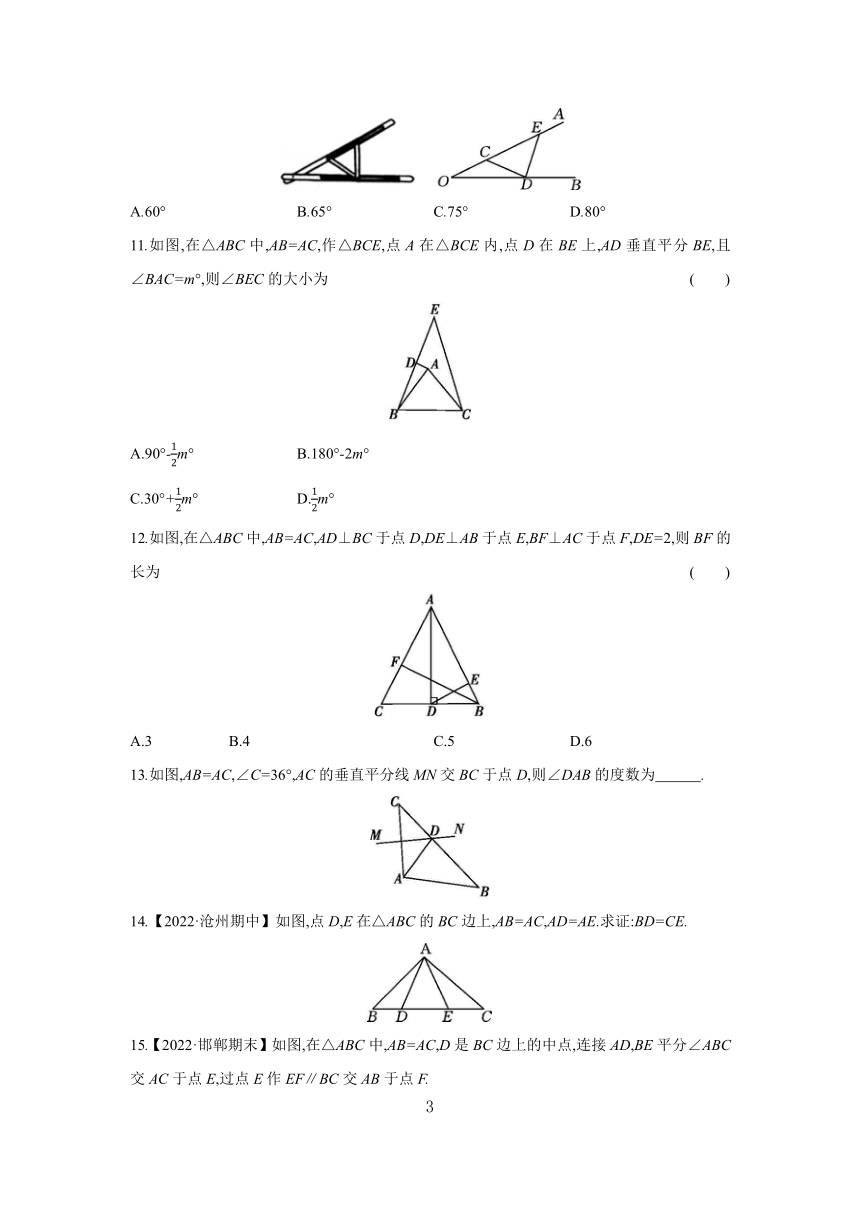
10.【河北期末】“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是 ( )
A.60° B.65° C.75° D.80°
11.如图,在△ABC中,AB=AC,作△BCE,点A在△BCE内,点D在BE上,AD垂直平分BE,且∠BAC=m°,则∠BEC的大小为 ( )
A.90°-m° B.180°-2m°
C.30°+m° D.m°
12.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为 ( )
A.3 B.4 C.5 D.6
13.如图,AB=AC,∠C=36°,AC的垂直平分线MN交BC于点D,则∠DAB的度数为 .
14.【2022·沧州期中】如图,点D,E在△ABC的BC边上,AB=AC,AD=AE.求证:BD=CE.
15.【2022·邯郸期末】如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数.
(2)求证:∠FBE=∠FEB.
【练素养】
16.在△ABC中,D,E是BC边上的两点,且BA=BD,CA=CE,连接AD,AE.
(1)如图1,若∠B=40°,∠C=60°,求∠DAE的度数.
(2)如图2,若∠BAC=α(0°<α<180°),求证:∠DAE=90°-α.
(3)若∠DAE=45°,则∠BAC的度数为 .
参考答案
练基础
1.B 2.B 3.B
4.80
5.D 6.A
7.20°
练能力
8.C 9.D 10.D 11.D 12.B
13.72°
14.【解析】证明:如图,过点A作AP⊥BC于点P.
∵AB=AC,AP⊥BC,∴BP=PC.
∵AD=AE,AP⊥BC,∴DP=PE,
∴BP-DP=PC-PE,∴BD=CE.
15.【解析】(1)∵AB=AC,∴∠C=∠ABC.
∵∠C=36°,∴∠ABC=36°.
∵AB=AC,BD=CD,∴AD⊥BC,∴∠ADB=90°,
∴∠BAD=90°-36°=54°.
(2)证明:∵BE平分∠ABC,∴∠ABE=∠CBE.
∵EF∥BC,∴∠FEB=∠CBE,∴∠FBE=∠FEB.
练素养
16.【解析】(1)∵BA=BD,∠B=40°,
∴∠BAD=∠BDA==70°.
∵CA=CE,∠C=60°,
∴∠AEC=∠EAC=60°.
∵∠DAE+∠AED+∠ADE=180°,
∴∠EAD=50°.
(2)证明:∵BA=BD,CA=CE,∴∠BAD=∠BDA=,∠AEC=∠EAC=.
∵∠BAD+∠CAE=∠BAC+∠DAE,
∴∠DAE=∠BAD+∠CAE-∠BAC=180°-(∠B+∠C)-∠BAC=180°-(180°-∠BAC)-∠BAC=90°-∠BAC=90°-α.
(3)90°.
提示:由(2)可知,∠DAE=90°-∠BAC,
∴∠BAC=180°-2∠DAE=180°-2×45°=90°.故答案为90°.
2
【练基础】
必备知识1 等边对等角
1.【2022·唐山期末】如图,在△ABC中,AB=AC,D为边AC上一点,且AD=BD,∠A=40°,则∠DBC的度数是 ( )
A.20° B.30° C.40° D.50°
2.如图,AB=AC,CD=CE.过点C的直线FG与DE平行,若∠A=38°,则∠1的度数为 ( )
A.42° B.54.5° C.58° D.62.5°
3.如图,在△ABC中,AB=AD=DC,∠B=64°,则∠C的度数为 ( )
A.30° B.32° C.40° D.48°
4.在等腰三角形ABC中,∠A=4∠B.若∠A为底角,则∠C= °.
必备知识2 等腰三角形“三线合一”
5.如图,在△ABC中,AB=AC,D是BC的中点,下列结论不正确的是 ( )
A.∠B=∠C B.AD⊥BC
C.AD平分∠BAC D.AB=2BD
6.如图,BE⊥AC于点D,且AB=BC,BD=ED,若∠ABC=54°,则∠E的大小为 ( )
A.27° B.36° C.40° D.54°
7.如图,在△ABC中,AB=AC.AD是BC边上的中线,点E在边AB上,且BD=BE.若∠BAC=100°,则∠ADE的大小为 .
【练能力】
8.在等腰△ABC中,∠A=70°,则∠C的度数不可能是 ( )
A.40° B.55° C.65° D.70°
9.如图,在△ABC中,AB=AC,以点B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则下列结论不一定成立的是 ( )
A.BC=BD
B.∠BDC=∠ABC
C.∠A=∠CBD
D.AD=BD
10.【河北期末】“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是 ( )
A.60° B.65° C.75° D.80°
11.如图,在△ABC中,AB=AC,作△BCE,点A在△BCE内,点D在BE上,AD垂直平分BE,且∠BAC=m°,则∠BEC的大小为 ( )
A.90°-m° B.180°-2m°
C.30°+m° D.m°
12.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为 ( )
A.3 B.4 C.5 D.6
13.如图,AB=AC,∠C=36°,AC的垂直平分线MN交BC于点D,则∠DAB的度数为 .
14.【2022·沧州期中】如图,点D,E在△ABC的BC边上,AB=AC,AD=AE.求证:BD=CE.
15.【2022·邯郸期末】如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数.
(2)求证:∠FBE=∠FEB.
【练素养】
16.在△ABC中,D,E是BC边上的两点,且BA=BD,CA=CE,连接AD,AE.
(1)如图1,若∠B=40°,∠C=60°,求∠DAE的度数.
(2)如图2,若∠BAC=α(0°<α<180°),求证:∠DAE=90°-α.
(3)若∠DAE=45°,则∠BAC的度数为 .
参考答案
练基础
1.B 2.B 3.B
4.80
5.D 6.A
7.20°
练能力
8.C 9.D 10.D 11.D 12.B
13.72°
14.【解析】证明:如图,过点A作AP⊥BC于点P.
∵AB=AC,AP⊥BC,∴BP=PC.
∵AD=AE,AP⊥BC,∴DP=PE,
∴BP-DP=PC-PE,∴BD=CE.
15.【解析】(1)∵AB=AC,∴∠C=∠ABC.
∵∠C=36°,∴∠ABC=36°.
∵AB=AC,BD=CD,∴AD⊥BC,∴∠ADB=90°,
∴∠BAD=90°-36°=54°.
(2)证明:∵BE平分∠ABC,∴∠ABE=∠CBE.
∵EF∥BC,∴∠FEB=∠CBE,∴∠FBE=∠FEB.
练素养
16.【解析】(1)∵BA=BD,∠B=40°,
∴∠BAD=∠BDA==70°.
∵CA=CE,∠C=60°,
∴∠AEC=∠EAC=60°.
∵∠DAE+∠AED+∠ADE=180°,
∴∠EAD=50°.
(2)证明:∵BA=BD,CA=CE,∴∠BAD=∠BDA=,∠AEC=∠EAC=.
∵∠BAD+∠CAE=∠BAC+∠DAE,
∴∠DAE=∠BAD+∠CAE-∠BAC=180°-(∠B+∠C)-∠BAC=180°-(180°-∠BAC)-∠BAC=90°-∠BAC=90°-α.
(3)90°.
提示:由(2)可知,∠DAE=90°-∠BAC,
∴∠BAC=180°-2∠DAE=180°-2×45°=90°.故答案为90°.
2
