13.3.1 课时2 等腰三角形的判定 分层作业 (含答案)2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 13.3.1 课时2 等腰三角形的判定 分层作业 (含答案)2023-2024学年数学人教版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 131.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 21:58:07 | ||
图片预览


文档简介
13.3.1 课时2 等腰三角形的判定
【练基础】
必备知识1 等角对等边
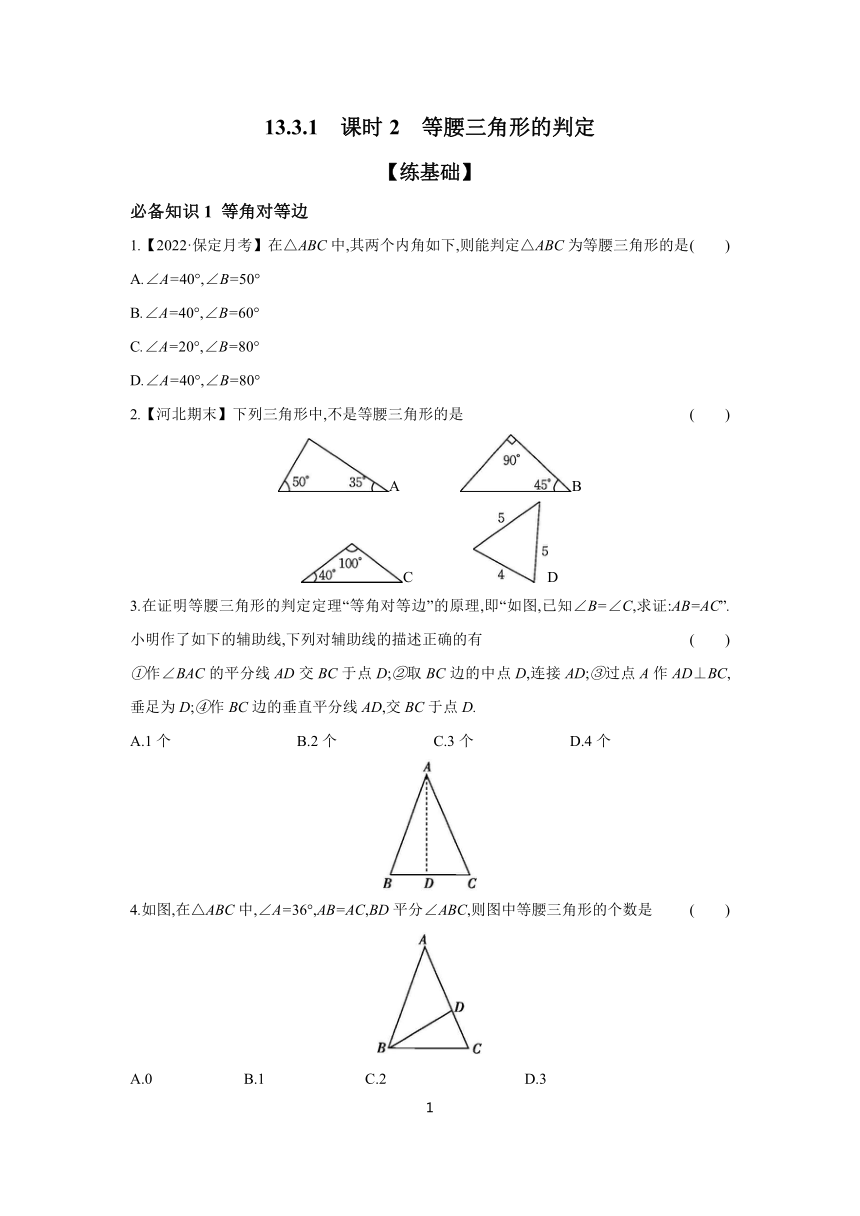
1.【2022·保定月考】在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是 ( )
A.∠A=40°,∠B=50°
B.∠A=40°,∠B=60°
C.∠A=20°,∠B=80°
D.∠A=40°,∠B=80°
2.【河北期末】下列三角形中,不是等腰三角形的是 ( )
A B
C D
3.在证明等腰三角形的判定定理“等角对等边”的原理,即“如图,已知∠B=∠C,求证:AB=AC”.小明作了如下的辅助线,下列对辅助线的描述正确的有 ( )
①作∠BAC的平分线AD交BC于点D;②取BC边的中点D,连接AD;③过点A作AD⊥BC,垂足为D;④作BC边的垂直平分线AD,交BC于点D.
A.1个 B.2个 C.3个 D.4个
4.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是 ( )
A.0 B.1 C.2 D.3
5.【2022·石家庄月考】如图,∠AOB=40°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为 .
必备知识2 等腰三角形的性质与判定的综合运用
6.在△ABC中,AD⊥BC,D为BC的中点,以下结论:①△ABD≌△ACD,②AB=AC,③∠B=∠C,④AD是△ABC的角平分线.正确的有 ( )
A.1个 B.2个 C.3个 D.4个
7.如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠B=39°,求∠CAD的度数.
(2)若点E在边AC上,EF∥AB交AD的延长线于点F.求证:AE=FE.
【练能力】
8.下列条件中,不能判定△ABC是等腰三角形的是 ( )
A.a=3,b=3,c=4
B.a∶b∶c=2∶3∶4
C.∠B=50°,∠C=80°
D.∠A∶∠B∶∠C=1∶1∶2
9.如图,已知每个小方格的边长为1,A,B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC是以AB为腰的等腰三角形,这样的格点C有 ( )
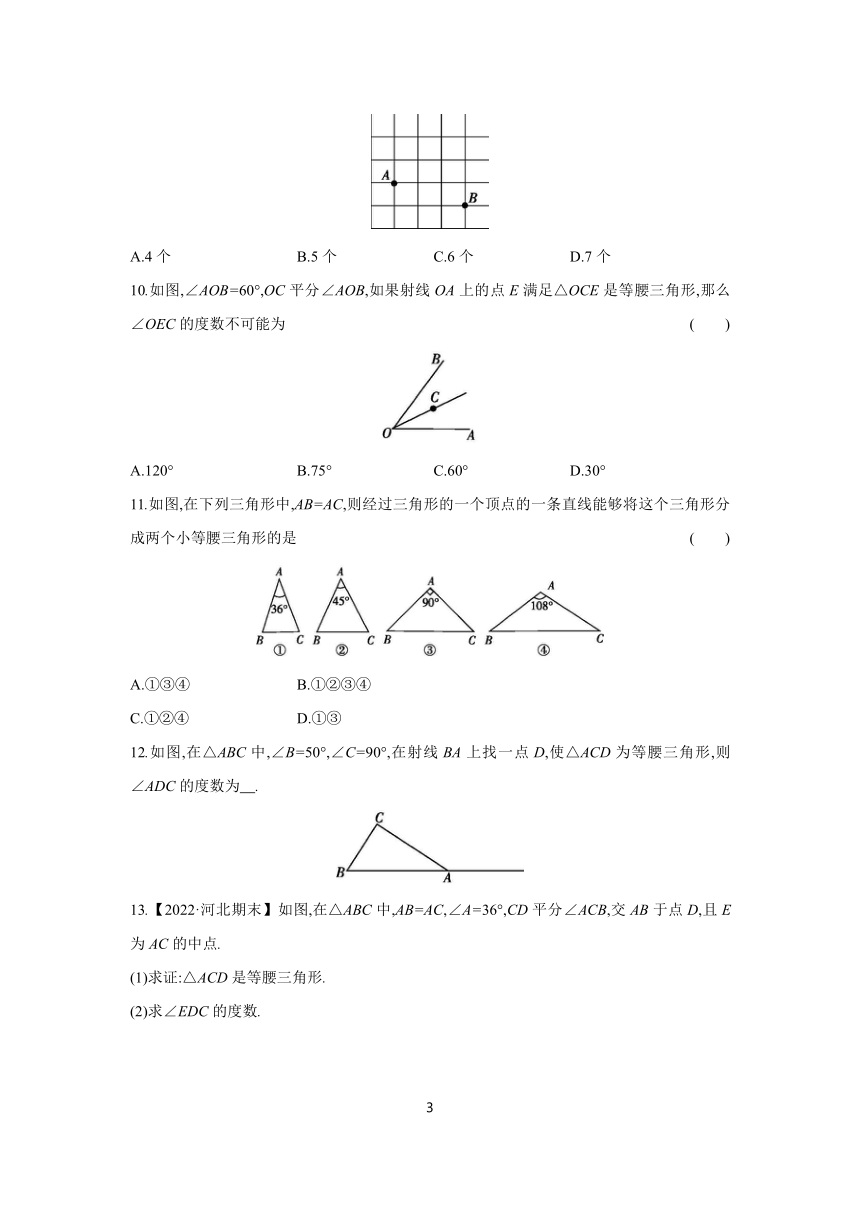
A.4个 B.5个 C.6个 D.7个
10.如图,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数不可能为 ( )
A.120° B.75° C.60° D.30°
11.如图,在下列三角形中,AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是 ( )
A.①③④ B.①②③④
C.①②④ D.①③
12.如图,在△ABC中,∠B=50°,∠C=90°,在射线BA上找一点D,使△ACD为等腰三角形,则∠ADC的度数为 .
13.【2022·河北期末】如图,在△ABC中,AB=AC,∠A=36°,CD平分∠ACB,交AB于点D,且E为AC的中点.
(1)求证:△ACD是等腰三角形.
(2)求∠EDC的度数.
14.如图,在△ABC中,∠ABC=∠ACB,点D,E分别在AB,AC上,DE∥BC,BE,CD相交于点F.
(1)求证:DC=EB.
(2)在不添加任何辅助线的情况下,请直接写出图中所有的等腰三角形.
【练素养】
15.如图,在△ABC中,AB=AC,M,N分别是AB,AC边上的点,并且MN∥BC.
(1)△AMN是否是等腰三角形 说明理由.
(2)P是MN上的一点,并且BP平分∠ABC,CP平分∠ACB.
①求证:△BPM是等腰三角形.
②若△ABC的周长为a,BC=b(a>2b),求△AMN的周长.(用含a,b的式子表示)
参考答案
练基础
1.C 2.A 3.B 4.D
5.140°或80°或20°
6.D
7.【解析】(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°.
又∵∠B=39°,
∴∠BAD=∠CAD=90°-39°=51°.
(2)证明:∵AB=AC,AD⊥BC于点D,∴∠BAD=∠CAD.∵EF∥AB,∴∠BAD=∠F,∴∠F=∠CAD,∴AE=FE.
练能力
8.B 9.C 10.C 11.A
12.70°或100°或20°
13.【解析】(1)证明:∵AB=AC,∠A=36°,
∴∠ACB=∠B=(180°-∠A)=72°.
∵CD平分∠ACB,
∴∠ACD=∠DCB=36°.
又∵∠A=36°,
∴CD=AD,即△ACD是等腰三角形.
(2)∵E是AC的中点,∴AE=EC.
又∵CD=AD,
∴∠DEC=90°,
∴∠EDC=90°-∠ACD=90°-36°=54°.
14.【解析】(1)证明:∵∠ABC=∠ACB,∴AB=AC.
∵DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,∴AD=AE,∴AB-AD=AC-AE,即BD=CE.
在△DBC和△ECB中,
∴△DBC≌△ECB(SAS),∴DC=EB.
(2)图中所有的等腰三角形为△ABC,△ADE,△DEF,△BCF.
练素养
15.【解析】(1)△AMN是等腰三角形,
理由:∵AB=AC,∴∠ABC=∠ACB.
∵MN∥BC,∴∠AMN=∠ABC,∠ANM=∠ACB,
∴∠AMN=∠ANM,∴AM=AN,∴△AMN是等腰三角形.
(2)①证明:∵BP平分∠ABC,∴∠PBM=∠PBC.
∵MN∥BC,∴∠MPB=∠PBC,∴∠PBM=∠MPB,
∴MB=MP,∴△BPM是等腰三角形.
②由①知MB=MP,同理可得NC=NP,
∴△AMN的周长=AM+MP+NP+AN=AM+MB+NC+AN=AB+AC.
∵△ABC的周长为a,BC=b,
∴AB+AC+b=a,
∴AB+AC=a-b,∴△AMN的周长=a-b.
2
【练基础】
必备知识1 等角对等边
1.【2022·保定月考】在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是 ( )
A.∠A=40°,∠B=50°
B.∠A=40°,∠B=60°
C.∠A=20°,∠B=80°
D.∠A=40°,∠B=80°
2.【河北期末】下列三角形中,不是等腰三角形的是 ( )
A B
C D
3.在证明等腰三角形的判定定理“等角对等边”的原理,即“如图,已知∠B=∠C,求证:AB=AC”.小明作了如下的辅助线,下列对辅助线的描述正确的有 ( )
①作∠BAC的平分线AD交BC于点D;②取BC边的中点D,连接AD;③过点A作AD⊥BC,垂足为D;④作BC边的垂直平分线AD,交BC于点D.
A.1个 B.2个 C.3个 D.4个
4.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是 ( )
A.0 B.1 C.2 D.3
5.【2022·石家庄月考】如图,∠AOB=40°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为 .
必备知识2 等腰三角形的性质与判定的综合运用
6.在△ABC中,AD⊥BC,D为BC的中点,以下结论:①△ABD≌△ACD,②AB=AC,③∠B=∠C,④AD是△ABC的角平分线.正确的有 ( )
A.1个 B.2个 C.3个 D.4个
7.如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠B=39°,求∠CAD的度数.
(2)若点E在边AC上,EF∥AB交AD的延长线于点F.求证:AE=FE.
【练能力】
8.下列条件中,不能判定△ABC是等腰三角形的是 ( )
A.a=3,b=3,c=4
B.a∶b∶c=2∶3∶4
C.∠B=50°,∠C=80°
D.∠A∶∠B∶∠C=1∶1∶2
9.如图,已知每个小方格的边长为1,A,B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC是以AB为腰的等腰三角形,这样的格点C有 ( )
A.4个 B.5个 C.6个 D.7个
10.如图,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数不可能为 ( )
A.120° B.75° C.60° D.30°
11.如图,在下列三角形中,AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是 ( )
A.①③④ B.①②③④
C.①②④ D.①③
12.如图,在△ABC中,∠B=50°,∠C=90°,在射线BA上找一点D,使△ACD为等腰三角形,则∠ADC的度数为 .
13.【2022·河北期末】如图,在△ABC中,AB=AC,∠A=36°,CD平分∠ACB,交AB于点D,且E为AC的中点.
(1)求证:△ACD是等腰三角形.
(2)求∠EDC的度数.
14.如图,在△ABC中,∠ABC=∠ACB,点D,E分别在AB,AC上,DE∥BC,BE,CD相交于点F.
(1)求证:DC=EB.
(2)在不添加任何辅助线的情况下,请直接写出图中所有的等腰三角形.
【练素养】
15.如图,在△ABC中,AB=AC,M,N分别是AB,AC边上的点,并且MN∥BC.
(1)△AMN是否是等腰三角形 说明理由.
(2)P是MN上的一点,并且BP平分∠ABC,CP平分∠ACB.
①求证:△BPM是等腰三角形.
②若△ABC的周长为a,BC=b(a>2b),求△AMN的周长.(用含a,b的式子表示)
参考答案
练基础
1.C 2.A 3.B 4.D
5.140°或80°或20°
6.D
7.【解析】(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°.
又∵∠B=39°,
∴∠BAD=∠CAD=90°-39°=51°.
(2)证明:∵AB=AC,AD⊥BC于点D,∴∠BAD=∠CAD.∵EF∥AB,∴∠BAD=∠F,∴∠F=∠CAD,∴AE=FE.
练能力
8.B 9.C 10.C 11.A
12.70°或100°或20°
13.【解析】(1)证明:∵AB=AC,∠A=36°,
∴∠ACB=∠B=(180°-∠A)=72°.
∵CD平分∠ACB,
∴∠ACD=∠DCB=36°.
又∵∠A=36°,
∴CD=AD,即△ACD是等腰三角形.
(2)∵E是AC的中点,∴AE=EC.
又∵CD=AD,
∴∠DEC=90°,
∴∠EDC=90°-∠ACD=90°-36°=54°.
14.【解析】(1)证明:∵∠ABC=∠ACB,∴AB=AC.
∵DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,∴AD=AE,∴AB-AD=AC-AE,即BD=CE.
在△DBC和△ECB中,
∴△DBC≌△ECB(SAS),∴DC=EB.
(2)图中所有的等腰三角形为△ABC,△ADE,△DEF,△BCF.
练素养
15.【解析】(1)△AMN是等腰三角形,
理由:∵AB=AC,∴∠ABC=∠ACB.
∵MN∥BC,∴∠AMN=∠ABC,∠ANM=∠ACB,
∴∠AMN=∠ANM,∴AM=AN,∴△AMN是等腰三角形.
(2)①证明:∵BP平分∠ABC,∴∠PBM=∠PBC.
∵MN∥BC,∴∠MPB=∠PBC,∴∠PBM=∠MPB,
∴MB=MP,∴△BPM是等腰三角形.
②由①知MB=MP,同理可得NC=NP,
∴△AMN的周长=AM+MP+NP+AN=AM+MB+NC+AN=AB+AC.
∵△ABC的周长为a,BC=b,
∴AB+AC+b=a,
∴AB+AC=a-b,∴△AMN的周长=a-b.
2
