13.3.2 课时1 等边三角形的性质与判定 分层作业 (含答案)2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 13.3.2 课时1 等边三角形的性质与判定 分层作业 (含答案)2023-2024学年数学人教版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 168.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 21:58:27 | ||
图片预览

文档简介
13.3.2 课时1 等边三角形的性质与判定
【练基础】
必备知识1 等边三角形的性质
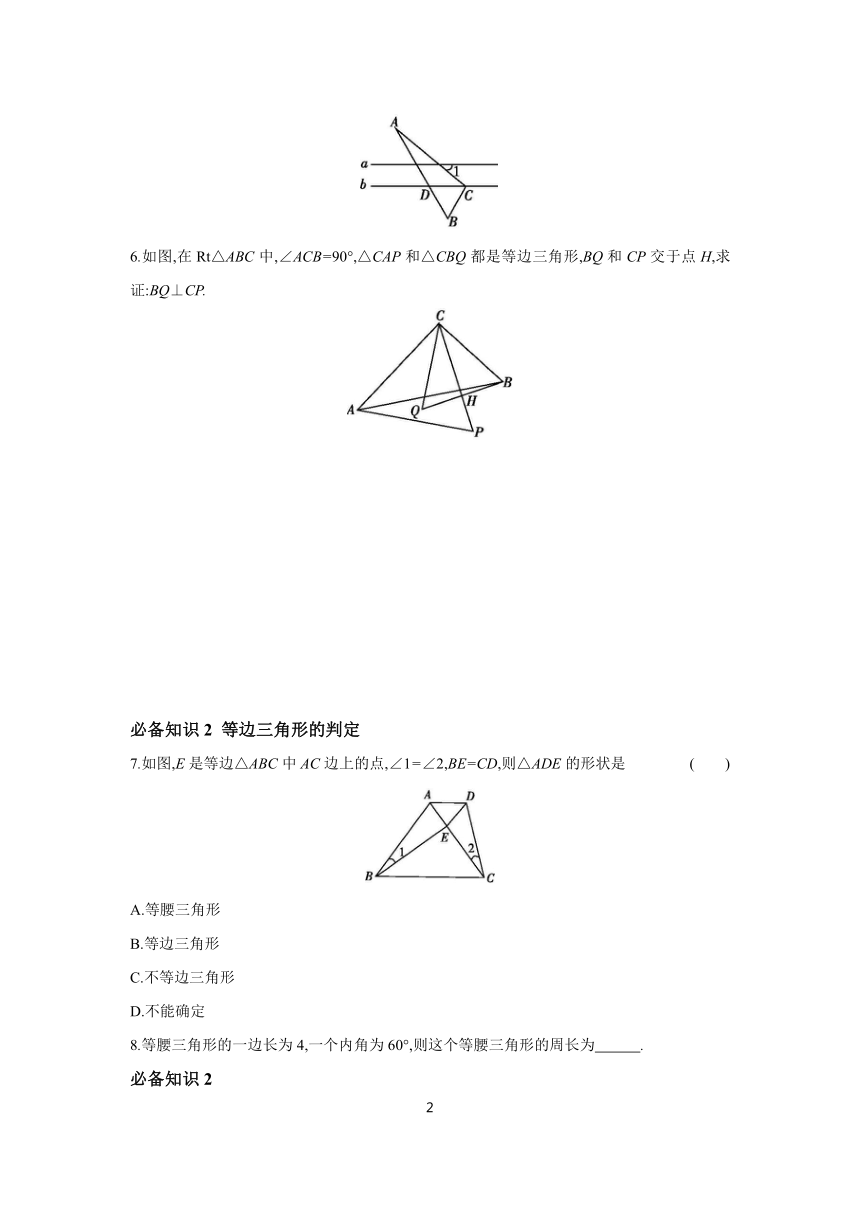
1.【2022·张家口月考】如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于 ( )
A.18° B.25° C.30° D.15°
2.如图,△ABC是等边三角形,BC=BD,∠BAD=20°,则∠BCD的度数为 ( )
A.50° B.55° C.60° D.65°
3.如图,过等边△ABC的顶点A作射线,若∠1=20°,则∠2的度数是 ( )
A.100° B.80°
C.60° D.40°
4.若等边△ABC的边长如图所示,则y的值为 .
5.如图,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=24°,则∠1的度数为 .
6.如图,在Rt△ABC中,∠ACB=90°,△CAP和△CBQ都是等边三角形,BQ和CP交于点H,求证:BQ⊥CP.
必备知识2 等边三角形的判定
7.如图,E是等边△ABC中AC边上的点,∠1=∠2,BE=CD,则△ADE的形状是 ( )
A.等腰三角形
B.等边三角形
C.不等边三角形
D.不能确定
8.等腰三角形的一边长为4,一个内角为60°,则这个等腰三角形的周长为 .
必备知识2
【练能力】
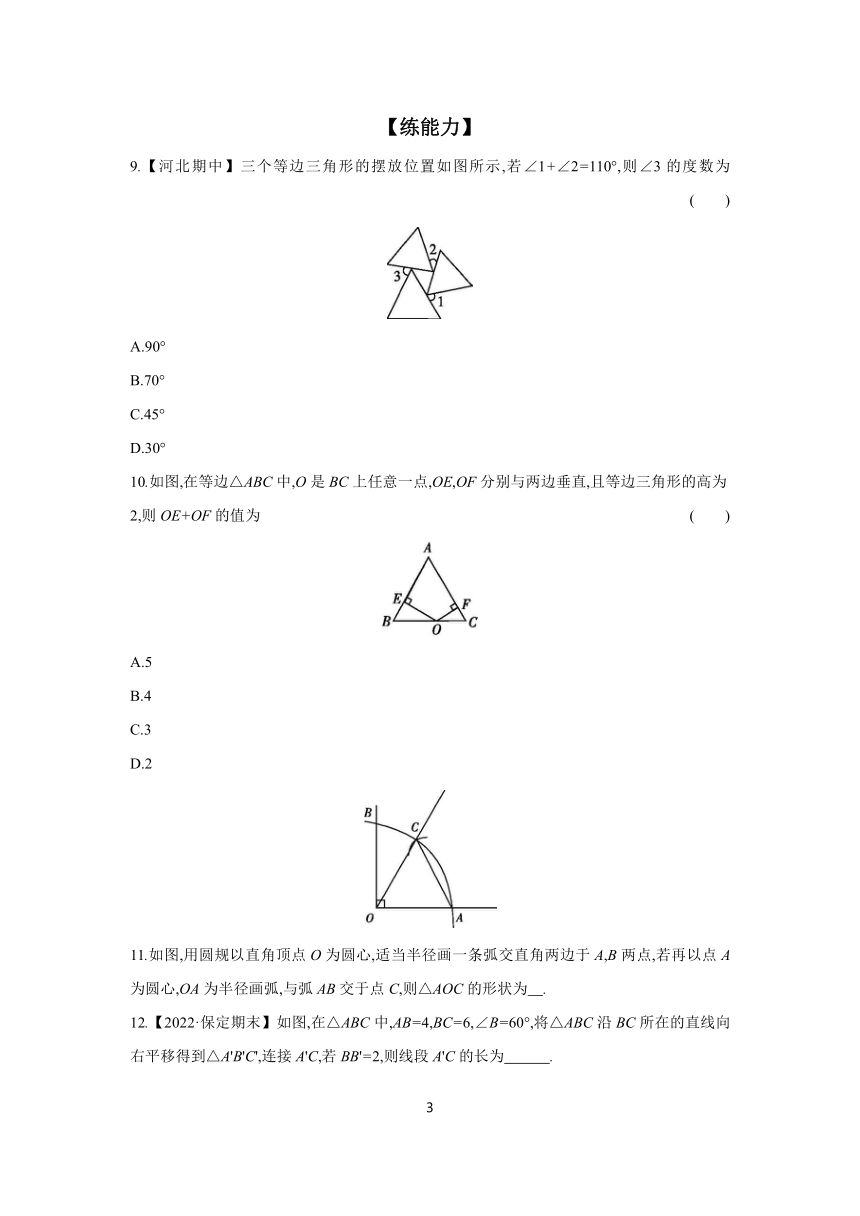
9.【河北期中】三个等边三角形的摆放位置如图所示,若∠1+∠2=110°,则∠3的度数为 ( )
A.90°
B.70°
C.45°
D.30°
10.如图,在等边△ABC中,O是BC上任意一点,OE,OF分别与两边垂直,且等边三角形的高为2,则OE+OF的值为 ( )
A.5
B.4
C.3
D.2
11.如图,用圆规以直角顶点O为圆心,适当半径画一条弧交直角两边于A,B两点,若再以点A为圆心,OA为半径画弧,与弧AB交于点C,则△AOC的形状为 .
12.【2022·保定期末】如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿BC所在的直线向右平移得到△A'B'C',连接A'C,若BB'=2,则线段A'C的长为 .
13.在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线.
(1)如图1,若AD=BD,求∠A的度数.
(2)如图2,在(1)的条件下,作DE⊥AB于点E,连接EC.求证:△EBC是等边三角形.
【练素养】
14.在△ABC中,AB=AC,在△ABC的外部作等边三角形△ACD,E为AC的中点,连接DE并延长交BC于点F,连接BD.
(1)如图1,若∠BAC=100°,求∠BDF的度数.
(2)如图2,∠ACB的平分线交AB于点M,交EF于点N,连接BN.
①补全图2.
②若BN=DN,求证:MB=MN.
参考答案
练基础
1.D 2.A 3.A
4.3.5
5.36°
6.【解析】证明:∵△CAP和△CBQ都是等边三角形,
∴∠ACP=∠CBQ=60°.
∵∠ACB=90°,
∴∠BCP=∠ACB-∠ACP=30°.
在△BCH中,∠BHC=180°-∠BCH-∠CBH=180°-30°-60°=90°,∴BQ⊥CP.
7.B
8.12
练能力
9.B 10.D
11.等边三角形
12.4
13.【解析】(1)∵AD=BD,∴∠A=∠DBA.
∵∠DBA=∠DBC,∴∠A=∠DBA=∠DBC.
∵∠ACB=90°,∴∠A+∠DBA+∠DBC=90°,
∴∠A=30°.
(2)证明:∵AD=BD,DE⊥AB,
∴AE=BE,∴CE=BE.
∵∠A=30°,∴∠EBC=60°,
∴△EBC是等边三角形.
练素养
14.【解析】(1)在等边△ACD中,∠CAD=∠ADC=60°,AD=AC.
∵E为AC的中点,
∴∠ADE=∠EDC=30°.
∵AB=AC,∴AD=AB.
∵∠BAD=∠BAC+∠CAD=160°,∴∠ADB=∠ABD=10°,
∴∠BDF=∠ADF-∠ADB=20°.
(2)①补全图形如图所示.
②证明:如图,连接AN.
∵CM平分∠ACB,∴设∠ACM=∠BCM=α.
∵AB=AC,
∴∠ABC=∠ACB=2α.
在等边△ACD中,
∵E为AC的中点,∴DN⊥AC,∴NA=NC,
∴∠NAC=∠NCA=α,∴∠DAN=60°+α.
在△ABN和△ADN中,
∴△ABN≌△ADN(SSS),
∴∠ABN=∠ADN=30°,∠BAN=∠DAN=60°+α,∴∠BAC=60°+2α.
在△ABC中,∠BAC+∠ACB+∠ABC=180°,
∴60°+2α+2α+2α=180°,∴α=20°,
∴∠NBC=∠ABC-∠ABN=10°,
∴∠MNB=∠NBC+∠NCB=30°,
∴∠MNB=∠MBN,∴MB=MN.
2
【练基础】
必备知识1 等边三角形的性质
1.【2022·张家口月考】如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于 ( )
A.18° B.25° C.30° D.15°
2.如图,△ABC是等边三角形,BC=BD,∠BAD=20°,则∠BCD的度数为 ( )
A.50° B.55° C.60° D.65°
3.如图,过等边△ABC的顶点A作射线,若∠1=20°,则∠2的度数是 ( )
A.100° B.80°
C.60° D.40°
4.若等边△ABC的边长如图所示,则y的值为 .
5.如图,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=24°,则∠1的度数为 .
6.如图,在Rt△ABC中,∠ACB=90°,△CAP和△CBQ都是等边三角形,BQ和CP交于点H,求证:BQ⊥CP.
必备知识2 等边三角形的判定
7.如图,E是等边△ABC中AC边上的点,∠1=∠2,BE=CD,则△ADE的形状是 ( )
A.等腰三角形
B.等边三角形
C.不等边三角形
D.不能确定
8.等腰三角形的一边长为4,一个内角为60°,则这个等腰三角形的周长为 .
必备知识2
【练能力】
9.【河北期中】三个等边三角形的摆放位置如图所示,若∠1+∠2=110°,则∠3的度数为 ( )
A.90°
B.70°
C.45°
D.30°
10.如图,在等边△ABC中,O是BC上任意一点,OE,OF分别与两边垂直,且等边三角形的高为2,则OE+OF的值为 ( )
A.5
B.4
C.3
D.2
11.如图,用圆规以直角顶点O为圆心,适当半径画一条弧交直角两边于A,B两点,若再以点A为圆心,OA为半径画弧,与弧AB交于点C,则△AOC的形状为 .
12.【2022·保定期末】如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿BC所在的直线向右平移得到△A'B'C',连接A'C,若BB'=2,则线段A'C的长为 .
13.在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线.
(1)如图1,若AD=BD,求∠A的度数.
(2)如图2,在(1)的条件下,作DE⊥AB于点E,连接EC.求证:△EBC是等边三角形.
【练素养】
14.在△ABC中,AB=AC,在△ABC的外部作等边三角形△ACD,E为AC的中点,连接DE并延长交BC于点F,连接BD.
(1)如图1,若∠BAC=100°,求∠BDF的度数.
(2)如图2,∠ACB的平分线交AB于点M,交EF于点N,连接BN.
①补全图2.
②若BN=DN,求证:MB=MN.
参考答案
练基础
1.D 2.A 3.A
4.3.5
5.36°
6.【解析】证明:∵△CAP和△CBQ都是等边三角形,
∴∠ACP=∠CBQ=60°.
∵∠ACB=90°,
∴∠BCP=∠ACB-∠ACP=30°.
在△BCH中,∠BHC=180°-∠BCH-∠CBH=180°-30°-60°=90°,∴BQ⊥CP.
7.B
8.12
练能力
9.B 10.D
11.等边三角形
12.4
13.【解析】(1)∵AD=BD,∴∠A=∠DBA.
∵∠DBA=∠DBC,∴∠A=∠DBA=∠DBC.
∵∠ACB=90°,∴∠A+∠DBA+∠DBC=90°,
∴∠A=30°.
(2)证明:∵AD=BD,DE⊥AB,
∴AE=BE,∴CE=BE.
∵∠A=30°,∴∠EBC=60°,
∴△EBC是等边三角形.
练素养
14.【解析】(1)在等边△ACD中,∠CAD=∠ADC=60°,AD=AC.
∵E为AC的中点,
∴∠ADE=∠EDC=30°.
∵AB=AC,∴AD=AB.
∵∠BAD=∠BAC+∠CAD=160°,∴∠ADB=∠ABD=10°,
∴∠BDF=∠ADF-∠ADB=20°.
(2)①补全图形如图所示.
②证明:如图,连接AN.
∵CM平分∠ACB,∴设∠ACM=∠BCM=α.
∵AB=AC,
∴∠ABC=∠ACB=2α.
在等边△ACD中,
∵E为AC的中点,∴DN⊥AC,∴NA=NC,
∴∠NAC=∠NCA=α,∴∠DAN=60°+α.
在△ABN和△ADN中,
∴△ABN≌△ADN(SSS),
∴∠ABN=∠ADN=30°,∠BAN=∠DAN=60°+α,∴∠BAC=60°+2α.
在△ABC中,∠BAC+∠ACB+∠ABC=180°,
∴60°+2α+2α+2α=180°,∴α=20°,
∴∠NBC=∠ABC-∠ABN=10°,
∴∠MNB=∠NBC+∠NCB=30°,
∴∠MNB=∠MBN,∴MB=MN.
2
