13.4 课题学习 最短路径问题 分层作业 (含答案)2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 13.4 课题学习 最短路径问题 分层作业 (含答案)2023-2024学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 207.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 21:59:02 | ||
图片预览

文档简介
13.4 课题学习 最短路径问题
【练基础】
必备知识 最短路径问题
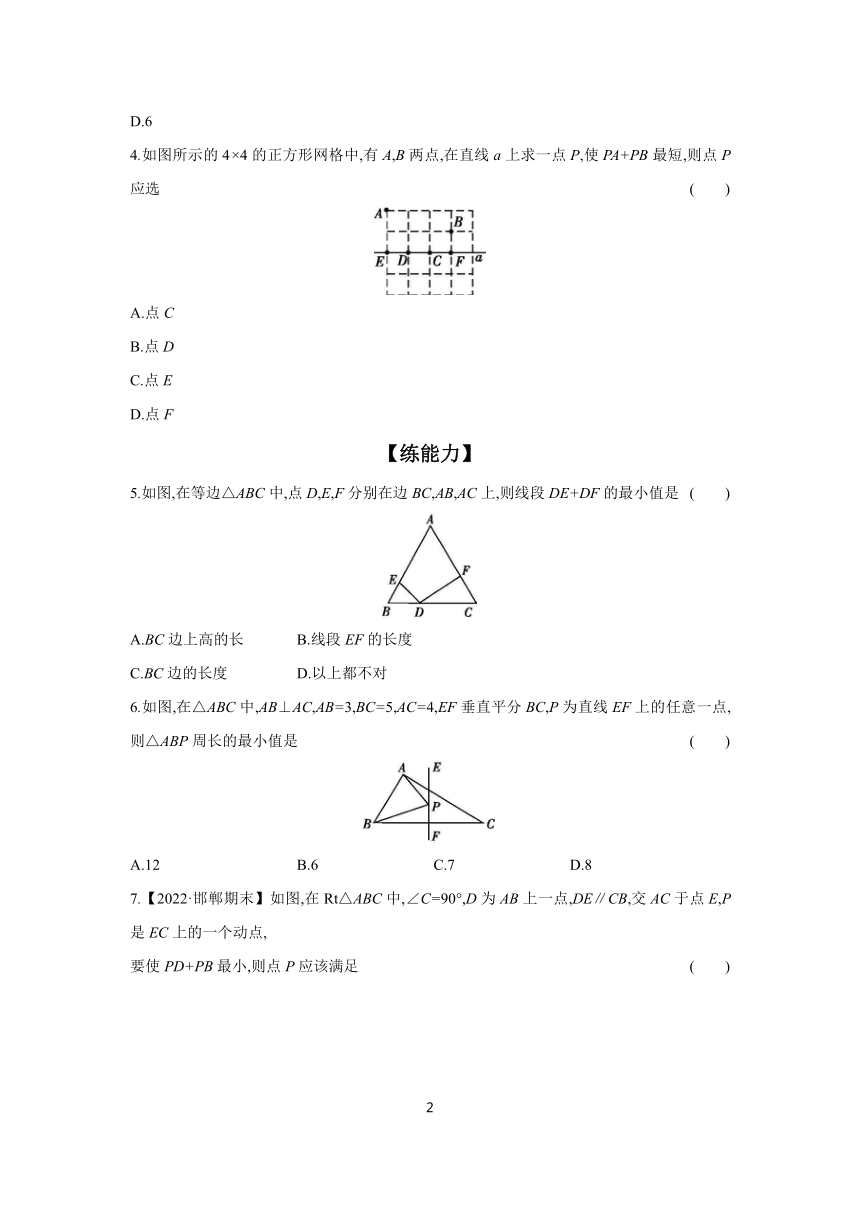
1.【2022·张家口月考】如图,A、B是两个居民小区,快递公司准备在公路l上选取点P处建一个服务中心,使PA+PB最短.下面四种选址方案符合要求的是 ( )
A B
C D
2.如图,已知∠O,P为其内一定点,分别在∠O的两边上找点A,B,使△PAB周长最小的是 ( )
A B C D
3.如图,在△ABC中,AB=4,AC=3,BC=5,EF是BC的垂直平分线,P是直线EF上的任意一点,则PA+PC的最小值是 ( )
A.3
B.4
C.5
D.6
4.如图所示的4×4的正方形网格中,有A,B两点,在直线a上求一点P,使PA+PB最短,则点P应选 ( )
A.点C
B.点D
C.点E
D.点F
【练能力】
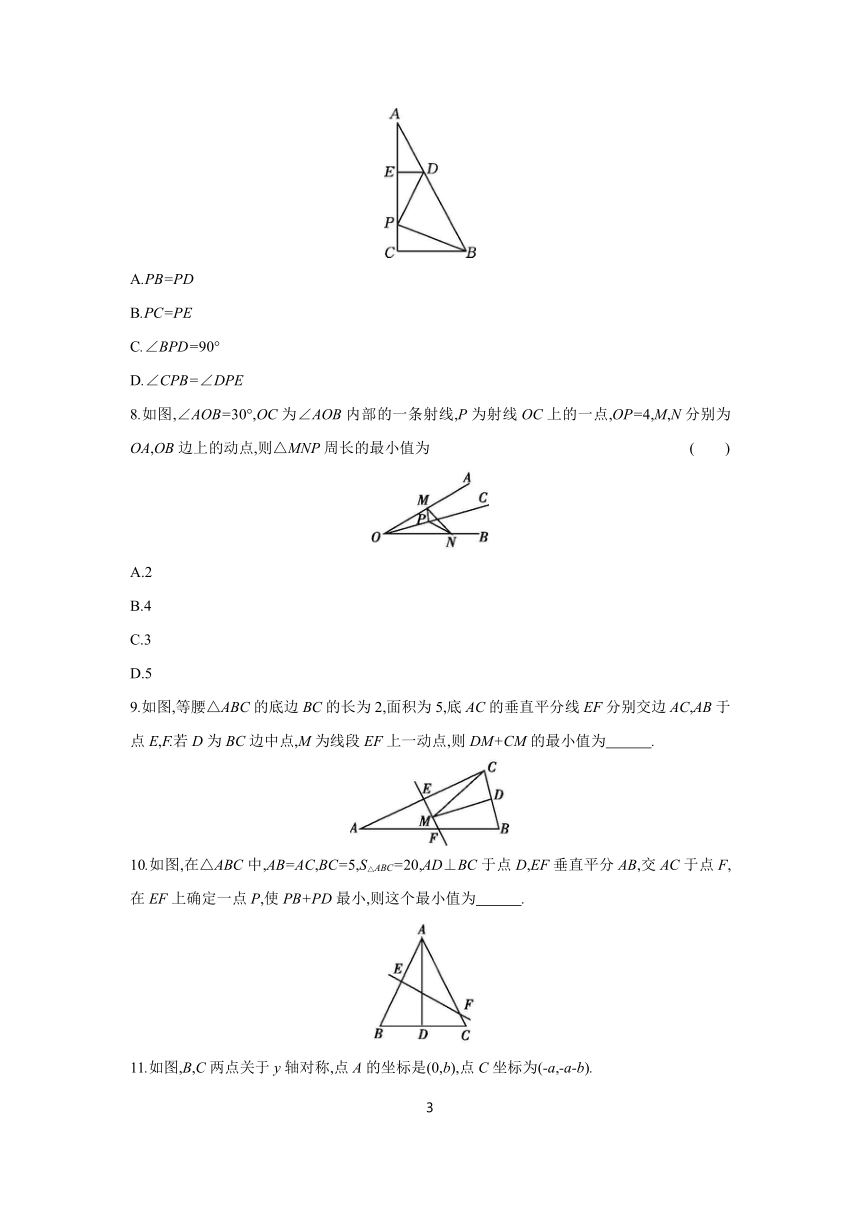
5.如图,在等边△ABC中,点D,E,F分别在边BC,AB,AC上,则线段DE+DF的最小值是 ( )
A.BC边上高的长 B.线段EF的长度
C.BC边的长度 D.以上都不对
6.如图,在△ABC中,AB⊥AC,AB=3,BC=5,AC=4,EF垂直平分BC,P为直线EF上的任意一点,则△ABP周长的最小值是 ( )
A.12 B.6 C.7 D.8
7.【2022·邯郸期末】如图,在Rt△ABC中,∠C=90°,D为AB上一点,DE∥CB,交AC于点E,P是EC上的一个动点,
要使PD+PB最小,则点P应该满足 ( )
A.PB=PD
B.PC=PE
C.∠BPD=90°
D.∠CPB=∠DPE
8.如图,∠AOB=30°,OC为∠AOB内部的一条射线,P为射线OC上的一点,OP=4,M,N分别为OA,OB边上的动点,则△MNP周长的最小值为 ( )
A.2
B.4
C.3
D.5
9.如图,等腰△ABC的底边BC的长为2,面积为5,底AC的垂直平分线EF分别交边AC,AB于点E,F.若D为BC边中点,M为线段EF上一动点,则DM+CM的最小值为 .
10.如图,在△ABC中,AB=AC,BC=5,S△ABC=20,AD⊥BC于点D,EF垂直平分AB,交AC于点F,在EF上确定一点P,使PB+PD最小,则这个最小值为 .
11.如图,B,C两点关于y轴对称,点A的坐标是(0,b),点C坐标为(-a,-a-b).
(1)直接写出点B的坐标: .
(2)用尺规作图,在x轴上作出点P,使得AP+PB的值最小.
(3)∠OAP的度数为 .
【练素养】
12.如图,某大学建立分校,校本部与分校隔着两条平行的小河,l1∥l2表示小河甲,l3∥l4表示小河乙,A为校本部大门,B为分校大门,为方便人员来往,要在两条小河上各建一座桥,桥面垂直于河岸.请你说明两桥应建在何处可使A,B两点间来往的路程最短
13.如图1,点P在∠AOB内,M,N分别是点P关于AO,BO的对称点,MN分别交OA,OB于点E,F.
(1)猜想△MON是哪种类型的三角形,并说明理由.
(2)猜想△PEF的周长与MN的长有什么关系,并说明理由.
(3)如图2,若∠AOB=30°,点P在∠AOB内,OP=a cm,M,N分别是点P关于AO,BO的对称点,E,F分别是射线OA,OB上的一点,连接PE,PF和EF.求△PEF周长的最小值.(用含a的式子表示)
2
参考答案
练基础
1.A 2.D 3.B 4.A
练能力
5.A 6.C 7.D 8.B
9.5
10.8
11.【解析】(1)(a,-a-b).
(2)如图,点P即所求.
(3)45°.
提示:过B作BD⊥y轴于点D,D(0,-a-b),则BD=-a,OD=-a-b,由(2)知A与A'关于x轴对称,∴A'O=AO=b,∴A'D=BD.在Rt△A'DB中,∠A'DB=90°,A'D=BD,∴∠BA'D=∠B=45°.∵点A与点A'关于x轴对称,∴∠OAP=∠DA'P=45°.
练素养
12.【解析】如图,
把点A向下平移河甲的宽度后得到点A',把点B向上平移河乙的宽度后得到点B',连接A'B'交l2于点D,交l3于点E,作CD⊥l1于点C,EF⊥l4于点F,连接AC,BF.则在CD,EF处建桥就是使得点A到点B总路程最短的桥的位置.
13.【解析】(1)△MON是等腰三角形.
理由:如图1,连接OP.
∵M,N分别是点P关于AO,BO的对称点,
∴OM=OP,ON=OP,
∴OM=ON,即△MON是等腰三角形.
(2)△PEF的周长等于MN的长.
理由:∵M,N分别是点P关于AO,BO的对称点,
∴ME=PE,NF=PF,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长.
(3)如图2,连接MN.
∵∠AOB=30°,
∴∠MON=2∠AOB=60°,
∴△MON为等边三角形,
∴MN=OM=ON=OP=a.
由(2)可知,当点E,F恰好在MN上时,△PEF的周长最小,此时,C△PEF=MN.
∴△PEF的周长最小值为a cm.
图1 图2
2
【练基础】
必备知识 最短路径问题
1.【2022·张家口月考】如图,A、B是两个居民小区,快递公司准备在公路l上选取点P处建一个服务中心,使PA+PB最短.下面四种选址方案符合要求的是 ( )
A B
C D
2.如图,已知∠O,P为其内一定点,分别在∠O的两边上找点A,B,使△PAB周长最小的是 ( )
A B C D
3.如图,在△ABC中,AB=4,AC=3,BC=5,EF是BC的垂直平分线,P是直线EF上的任意一点,则PA+PC的最小值是 ( )
A.3
B.4
C.5
D.6
4.如图所示的4×4的正方形网格中,有A,B两点,在直线a上求一点P,使PA+PB最短,则点P应选 ( )
A.点C
B.点D
C.点E
D.点F
【练能力】
5.如图,在等边△ABC中,点D,E,F分别在边BC,AB,AC上,则线段DE+DF的最小值是 ( )
A.BC边上高的长 B.线段EF的长度
C.BC边的长度 D.以上都不对
6.如图,在△ABC中,AB⊥AC,AB=3,BC=5,AC=4,EF垂直平分BC,P为直线EF上的任意一点,则△ABP周长的最小值是 ( )
A.12 B.6 C.7 D.8
7.【2022·邯郸期末】如图,在Rt△ABC中,∠C=90°,D为AB上一点,DE∥CB,交AC于点E,P是EC上的一个动点,
要使PD+PB最小,则点P应该满足 ( )
A.PB=PD
B.PC=PE
C.∠BPD=90°
D.∠CPB=∠DPE
8.如图,∠AOB=30°,OC为∠AOB内部的一条射线,P为射线OC上的一点,OP=4,M,N分别为OA,OB边上的动点,则△MNP周长的最小值为 ( )
A.2
B.4
C.3
D.5
9.如图,等腰△ABC的底边BC的长为2,面积为5,底AC的垂直平分线EF分别交边AC,AB于点E,F.若D为BC边中点,M为线段EF上一动点,则DM+CM的最小值为 .
10.如图,在△ABC中,AB=AC,BC=5,S△ABC=20,AD⊥BC于点D,EF垂直平分AB,交AC于点F,在EF上确定一点P,使PB+PD最小,则这个最小值为 .
11.如图,B,C两点关于y轴对称,点A的坐标是(0,b),点C坐标为(-a,-a-b).
(1)直接写出点B的坐标: .
(2)用尺规作图,在x轴上作出点P,使得AP+PB的值最小.
(3)∠OAP的度数为 .
【练素养】
12.如图,某大学建立分校,校本部与分校隔着两条平行的小河,l1∥l2表示小河甲,l3∥l4表示小河乙,A为校本部大门,B为分校大门,为方便人员来往,要在两条小河上各建一座桥,桥面垂直于河岸.请你说明两桥应建在何处可使A,B两点间来往的路程最短
13.如图1,点P在∠AOB内,M,N分别是点P关于AO,BO的对称点,MN分别交OA,OB于点E,F.
(1)猜想△MON是哪种类型的三角形,并说明理由.
(2)猜想△PEF的周长与MN的长有什么关系,并说明理由.
(3)如图2,若∠AOB=30°,点P在∠AOB内,OP=a cm,M,N分别是点P关于AO,BO的对称点,E,F分别是射线OA,OB上的一点,连接PE,PF和EF.求△PEF周长的最小值.(用含a的式子表示)
2
参考答案
练基础
1.A 2.D 3.B 4.A
练能力
5.A 6.C 7.D 8.B
9.5
10.8
11.【解析】(1)(a,-a-b).
(2)如图,点P即所求.
(3)45°.
提示:过B作BD⊥y轴于点D,D(0,-a-b),则BD=-a,OD=-a-b,由(2)知A与A'关于x轴对称,∴A'O=AO=b,∴A'D=BD.在Rt△A'DB中,∠A'DB=90°,A'D=BD,∴∠BA'D=∠B=45°.∵点A与点A'关于x轴对称,∴∠OAP=∠DA'P=45°.
练素养
12.【解析】如图,
把点A向下平移河甲的宽度后得到点A',把点B向上平移河乙的宽度后得到点B',连接A'B'交l2于点D,交l3于点E,作CD⊥l1于点C,EF⊥l4于点F,连接AC,BF.则在CD,EF处建桥就是使得点A到点B总路程最短的桥的位置.
13.【解析】(1)△MON是等腰三角形.
理由:如图1,连接OP.
∵M,N分别是点P关于AO,BO的对称点,
∴OM=OP,ON=OP,
∴OM=ON,即△MON是等腰三角形.
(2)△PEF的周长等于MN的长.
理由:∵M,N分别是点P关于AO,BO的对称点,
∴ME=PE,NF=PF,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长.
(3)如图2,连接MN.
∵∠AOB=30°,
∴∠MON=2∠AOB=60°,
∴△MON为等边三角形,
∴MN=OM=ON=OP=a.
由(2)可知,当点E,F恰好在MN上时,△PEF的周长最小,此时,C△PEF=MN.
∴△PEF的周长最小值为a cm.
图1 图2
2
