2023-2024学年数学人教版八年级上册第十二章 全等三角形 分层作业 (含答案)
文档属性
| 名称 | 2023-2024学年数学人教版八年级上册第十二章 全等三角形 分层作业 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 246.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 22:57:50 | ||
图片预览




文档简介
第十二章 全等三角形 自我评估
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列四组图形中,是全等图形的一组是 ( )
A B C D
2.如图,这是两个全等三角形,图中的字母表示三角形的边长,则∠1等于 ( )
A.66°
B.60°
C.56°
D.54°
3.如图,公园里有一座假山,要测假山两端A,B的距离,先在平地上取一个可直接到达A和B的点C,分别延长AC,BC到点D,E,使CD=CA,CE=CB,连接DE.这样就可利用三角形全等,通过量出DE的长得到假山两端A,B的距离.其中说明两个三角形全等的依据是 ( )
A.SSS B.ASA C.AAS D.SAS
4.如图,OB是∠AOC的平分线,D,E,F分别是射线OA、射线OB、射线OC上的点,连接ED,EF.若添加一个条件使△DOE≌△FOE,则这个条件可以为 ( )
A.∠ODE=∠OFE
B.∠ODE=∠BEF
C.OE=OF
D.OD=OE
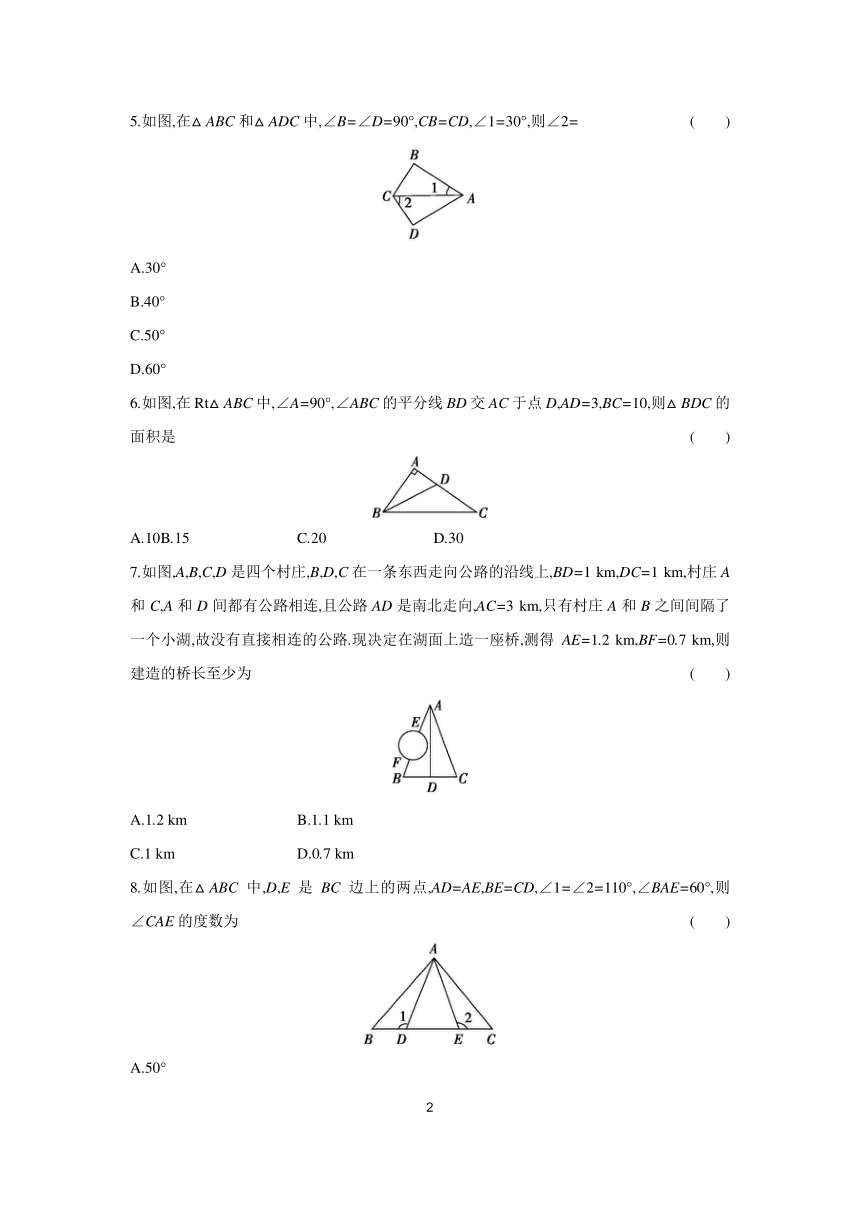
5.如图,在△ABC和△ADC中,∠B=∠D=90°,CB=CD,∠1=30°,则∠2= ( )
A.30°
B.40°
C.50°
D.60°
6.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 ( )
A.10 B.15 C.20 D.30
7.如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1 km,DC=1 km,村庄A和C,A和D间都有公路相连,且公路AD是南北走向,AC=3 km,只有村庄A和B之间间隔了一个小湖,故没有直接相连的公路.现决定在湖面上造一座桥,测得AE=1.2 km,BF=0.7 km,则建造的桥长至少为 ( )
A.1.2 km B.1.1 km
C.1 km D.0.7 km
8.如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE的度数为 ( )
A.50°
B.60°
C.40°
D.20°
9.如图,在网格纸中,每个小正方形的边长1,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有 ( )
A.1个
B.2个
C.3个
D.4个
10.如图,这是三条两两相交的公路,某石化公司拟建立一个加油站,计划使得该加油站到三条公路的距离相等,则加油站的可选位置有 ( )
A.1个
B.2个
C.3个
D.4个
二、填空题(本大题共5小题,每小题3分,共15分)
11.如图,在△ABC中,∠A∶∠ABC∶∠ACB=3∶5∶10,△MNC≌△BAC,则∠BCN的度数为 .
12.如图,在△ABC中,∠B=42°,AD⊥BC于点D,E是BD上一点,EF⊥AB于点F,若ED=EF,则∠AEC的度数为 °.
13.如图,在Rt△ABC中,∠ACB=90°,BC=4 cm,CD⊥AB,在AC上取一点E,使EC=4 cm,过点E作EF⊥AC交CD的延长线于点F.若AE=1 cm,则EF= cm.
14.如图,把长短确定的两根木棍AB,AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定,木棍AC绕A转动,得到△ABD,这个实验说明 .
15.如图,在△ABC中,∠ABC=∠C,D,E分别是AC,BC上的点,连接AE,BD交于点F,∠BFE=∠BAC,2∠AEB=∠BAC.若BD平分∠ABC,BE=m,AF=n,则△BEF的面积= .(用含m,n的式子表示)
三、解答题(本大题共7小题,共55分)
16.(6分)在一次数学课上,李老师在黑板上画出图(如图所示),并写出三个等式:
①AB=DC,②AC=DB,③∠BAD=∠CDA,要求同学从这三个等式中选出两个作为条件推出∠B=∠C,请你试着完成李老师提出的要求,并说明理由.
已知: (写一种情况即可),求证:∠B=∠C.
17.(6分)如图,BE,AD是△ABC的高且相交于点P,Q是BE延长线上的一点.
(1)求证:∠1=∠2.
(2)若AP=BC,AC=BQ.
①嘉嘉说:∠3和∠4一定相等.
②淇淇说:线段CP与CQ一定相等.
请你对嘉嘉的说法直接给出对错;对淇淇的说法加以说理判断.
18.(7分)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
(1)求证:△BDE≌△CDF.
(2)当AD⊥BC,AE=1,CF=2时,求AC的长.
19.(8分)如图,小刚站在河边的点A处,在河的对面(小刚的正北方向)B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树C处,接着再向前走了30步到达D处,然后他左转90°直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他共走了140步.
(1)根据题意,画出示意图.
(2)如果小刚走的一步大约50厘米,估计小刚在点A处时他与电线塔的距离,并说明理由.
20.(8分)如图,在五边形ABCDE中,∠B=∠E=90°,BC=DE,连接AC,AD,AD=AC.
(1)求证:△ABC≌△AED.
(2)若AC∥DE,∠ACD=65°,求∠BAE的度数.
21.(9分)如图,在四边形ABCD中,∠DAB和∠DCB互补,CD=CB,CE⊥AB于点E.
(1)求证:AC平分∠DAB.
(2)试猜想AB,AD,AE的数量关系,并证明你的猜想.
22.(11分)在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图,当点D在BC延长线上移动时,若∠BAC=25°,求∠DCE的度数.
(2)设∠BAC=α,∠DCE=β.
①当点D在BC延长线上移动时,α与β之间有什么数量关系 请直接写出你的结论.
②当点D在直线BC上(不与B,C两点重合)移动时,α与β之间有什么数量关系 请直接写出你的结论.
参考答案
1.D 2.A 3.D 4.A 5.D 6.B 7.B 8.D 9.C
10.C
11.20°
12.66
13.5
14.有两边和其中一边的对角分别相等的两个三角形不一定全等
15.mn
16.【解析】解法1:已知:①②,
证明:在△ABD和△DCA中,
∴△ABD≌△DCA(SSS),
∴∠B=∠C.
解法2:已知:①③.
证明:在△ABD和△DCA中,
∴△ABD≌△DCA(SAS),
∴∠B=∠C.
17.【解析】(1)证明:∵BE,AD是△ABC的高,∴∠BEC=∠ADC=90°,
∴∠1+∠BCE=90°,∠2+∠ACD=90°,∴∠1=∠2.
(2)嘉嘉的说法错误,淇淇的说法正确.
理由如下:由(1)得∠1=∠2,
在△APC和△BCQ中,
∴△APC≌△BCQ(SAS),∴CP=QC.
18.【解析】(1)(证法不唯一)证明:∵CF∥AB,
∴∠B=∠FCD,∠BED=∠F.
∵AD是BC边上的中线,
∴BD=CD.
在△BDE与△CDF中,
∴△BDE≌△CDF(AAS).
(2)∵△BDE≌△CDF,
∴BE=CF=2,
∴AB=AE+BE=1+2=3.
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在△ABD与△ACD中,
∴△ABD≌△ACD(SAS),
∴AC=AB=3.
19.【解析】(1)所画示意图如下:
(2)在△ABC和△DEC中,
∴△ABC≌△DEC(ASA),
∴AB=DE.
又∵小刚共走了140步,其中AD走了60步,
∴走完DE用了80步,
∴小刚走的一步大约50厘米,
∴DE=80×0.5=40(米).
答:小刚在点A处时他与电线塔的距离为40米.
20.【解析】(1)证明:∵∠B=∠E=90°,
∴△ABC和△AED都是直角三角形.
在Rt△ABC和Rt△AED中,
∴Rt△ABC≌Rt△AED(HL).
(2)过点A作AP⊥CD于点P.(图略)
∵AC=AD,AP=AP,
∴Rt△ADP≌Rt△ACP(HL),
∴∠ACD=∠ADC=65°,
∴∠DAC=180°-65°×2=50°.
∵AC∥DE,∴∠E+∠EAC=180°.
∵∠E=90°,∴∠EAC=90°.
∵Rt△ABC≌Rt△AED,
∴∠BAC=∠DAE=90°-∠DAC=90°-50°=40°,
∴∠BAE=∠EAC+∠BAC=130°.
21.【解析】(1)证明:如图,过点C作CF⊥AD交AD的延长线于点F.
∵∠DAB和∠DCB互补,∴∠ADC+∠B=180°.
∵∠ADC+∠FDC=180°,∴∠B=∠FDC.
∵CE⊥AB,CF⊥AD,∴∠CEB=∠F=90°.
在△CFD和△CEB中,
∴△CFD≌△CEB(AAS),∴CF=CE.
∵CE⊥AB,CF⊥AD,∴AC平分∠DAB.
(2)猜想:AB+AD=2AE.
证明:由(1)知△CFD≌△CEB,
∴CF=CE,DF=BE.
∵∠AEC=∠F=90°,AC=AC,
∴Rt△AEC≌Rt△AFC(HL),
∴AE=AF.
∵AB=AE+BE,AD=AF-DF=AE-BE,
∴AB+AD=2AE.
22.【解析】(1)∵∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE.
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,
∴∠BAC=∠DCE.
∵∠BAC=25°,
∴∠DCE=25°.
(2)①当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β.
②如图1,当点D在线段BC上时,α+β=180°;如图2,当点D在BC延长线或反向延长线上时,α=β.
2
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列四组图形中,是全等图形的一组是 ( )
A B C D
2.如图,这是两个全等三角形,图中的字母表示三角形的边长,则∠1等于 ( )
A.66°
B.60°
C.56°
D.54°
3.如图,公园里有一座假山,要测假山两端A,B的距离,先在平地上取一个可直接到达A和B的点C,分别延长AC,BC到点D,E,使CD=CA,CE=CB,连接DE.这样就可利用三角形全等,通过量出DE的长得到假山两端A,B的距离.其中说明两个三角形全等的依据是 ( )
A.SSS B.ASA C.AAS D.SAS
4.如图,OB是∠AOC的平分线,D,E,F分别是射线OA、射线OB、射线OC上的点,连接ED,EF.若添加一个条件使△DOE≌△FOE,则这个条件可以为 ( )
A.∠ODE=∠OFE
B.∠ODE=∠BEF
C.OE=OF
D.OD=OE
5.如图,在△ABC和△ADC中,∠B=∠D=90°,CB=CD,∠1=30°,则∠2= ( )
A.30°
B.40°
C.50°
D.60°
6.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 ( )
A.10 B.15 C.20 D.30
7.如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1 km,DC=1 km,村庄A和C,A和D间都有公路相连,且公路AD是南北走向,AC=3 km,只有村庄A和B之间间隔了一个小湖,故没有直接相连的公路.现决定在湖面上造一座桥,测得AE=1.2 km,BF=0.7 km,则建造的桥长至少为 ( )
A.1.2 km B.1.1 km
C.1 km D.0.7 km
8.如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE的度数为 ( )
A.50°
B.60°
C.40°
D.20°
9.如图,在网格纸中,每个小正方形的边长1,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有 ( )
A.1个
B.2个
C.3个
D.4个
10.如图,这是三条两两相交的公路,某石化公司拟建立一个加油站,计划使得该加油站到三条公路的距离相等,则加油站的可选位置有 ( )
A.1个
B.2个
C.3个
D.4个
二、填空题(本大题共5小题,每小题3分,共15分)
11.如图,在△ABC中,∠A∶∠ABC∶∠ACB=3∶5∶10,△MNC≌△BAC,则∠BCN的度数为 .
12.如图,在△ABC中,∠B=42°,AD⊥BC于点D,E是BD上一点,EF⊥AB于点F,若ED=EF,则∠AEC的度数为 °.
13.如图,在Rt△ABC中,∠ACB=90°,BC=4 cm,CD⊥AB,在AC上取一点E,使EC=4 cm,过点E作EF⊥AC交CD的延长线于点F.若AE=1 cm,则EF= cm.
14.如图,把长短确定的两根木棍AB,AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定,木棍AC绕A转动,得到△ABD,这个实验说明 .
15.如图,在△ABC中,∠ABC=∠C,D,E分别是AC,BC上的点,连接AE,BD交于点F,∠BFE=∠BAC,2∠AEB=∠BAC.若BD平分∠ABC,BE=m,AF=n,则△BEF的面积= .(用含m,n的式子表示)
三、解答题(本大题共7小题,共55分)
16.(6分)在一次数学课上,李老师在黑板上画出图(如图所示),并写出三个等式:
①AB=DC,②AC=DB,③∠BAD=∠CDA,要求同学从这三个等式中选出两个作为条件推出∠B=∠C,请你试着完成李老师提出的要求,并说明理由.
已知: (写一种情况即可),求证:∠B=∠C.
17.(6分)如图,BE,AD是△ABC的高且相交于点P,Q是BE延长线上的一点.
(1)求证:∠1=∠2.
(2)若AP=BC,AC=BQ.
①嘉嘉说:∠3和∠4一定相等.
②淇淇说:线段CP与CQ一定相等.
请你对嘉嘉的说法直接给出对错;对淇淇的说法加以说理判断.
18.(7分)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
(1)求证:△BDE≌△CDF.
(2)当AD⊥BC,AE=1,CF=2时,求AC的长.
19.(8分)如图,小刚站在河边的点A处,在河的对面(小刚的正北方向)B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树C处,接着再向前走了30步到达D处,然后他左转90°直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他共走了140步.
(1)根据题意,画出示意图.
(2)如果小刚走的一步大约50厘米,估计小刚在点A处时他与电线塔的距离,并说明理由.
20.(8分)如图,在五边形ABCDE中,∠B=∠E=90°,BC=DE,连接AC,AD,AD=AC.
(1)求证:△ABC≌△AED.
(2)若AC∥DE,∠ACD=65°,求∠BAE的度数.
21.(9分)如图,在四边形ABCD中,∠DAB和∠DCB互补,CD=CB,CE⊥AB于点E.
(1)求证:AC平分∠DAB.
(2)试猜想AB,AD,AE的数量关系,并证明你的猜想.
22.(11分)在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图,当点D在BC延长线上移动时,若∠BAC=25°,求∠DCE的度数.
(2)设∠BAC=α,∠DCE=β.
①当点D在BC延长线上移动时,α与β之间有什么数量关系 请直接写出你的结论.
②当点D在直线BC上(不与B,C两点重合)移动时,α与β之间有什么数量关系 请直接写出你的结论.
参考答案
1.D 2.A 3.D 4.A 5.D 6.B 7.B 8.D 9.C
10.C
11.20°
12.66
13.5
14.有两边和其中一边的对角分别相等的两个三角形不一定全等
15.mn
16.【解析】解法1:已知:①②,
证明:在△ABD和△DCA中,
∴△ABD≌△DCA(SSS),
∴∠B=∠C.
解法2:已知:①③.
证明:在△ABD和△DCA中,
∴△ABD≌△DCA(SAS),
∴∠B=∠C.
17.【解析】(1)证明:∵BE,AD是△ABC的高,∴∠BEC=∠ADC=90°,
∴∠1+∠BCE=90°,∠2+∠ACD=90°,∴∠1=∠2.
(2)嘉嘉的说法错误,淇淇的说法正确.
理由如下:由(1)得∠1=∠2,
在△APC和△BCQ中,
∴△APC≌△BCQ(SAS),∴CP=QC.
18.【解析】(1)(证法不唯一)证明:∵CF∥AB,
∴∠B=∠FCD,∠BED=∠F.
∵AD是BC边上的中线,
∴BD=CD.
在△BDE与△CDF中,
∴△BDE≌△CDF(AAS).
(2)∵△BDE≌△CDF,
∴BE=CF=2,
∴AB=AE+BE=1+2=3.
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在△ABD与△ACD中,
∴△ABD≌△ACD(SAS),
∴AC=AB=3.
19.【解析】(1)所画示意图如下:
(2)在△ABC和△DEC中,
∴△ABC≌△DEC(ASA),
∴AB=DE.
又∵小刚共走了140步,其中AD走了60步,
∴走完DE用了80步,
∴小刚走的一步大约50厘米,
∴DE=80×0.5=40(米).
答:小刚在点A处时他与电线塔的距离为40米.
20.【解析】(1)证明:∵∠B=∠E=90°,
∴△ABC和△AED都是直角三角形.
在Rt△ABC和Rt△AED中,
∴Rt△ABC≌Rt△AED(HL).
(2)过点A作AP⊥CD于点P.(图略)
∵AC=AD,AP=AP,
∴Rt△ADP≌Rt△ACP(HL),
∴∠ACD=∠ADC=65°,
∴∠DAC=180°-65°×2=50°.
∵AC∥DE,∴∠E+∠EAC=180°.
∵∠E=90°,∴∠EAC=90°.
∵Rt△ABC≌Rt△AED,
∴∠BAC=∠DAE=90°-∠DAC=90°-50°=40°,
∴∠BAE=∠EAC+∠BAC=130°.
21.【解析】(1)证明:如图,过点C作CF⊥AD交AD的延长线于点F.
∵∠DAB和∠DCB互补,∴∠ADC+∠B=180°.
∵∠ADC+∠FDC=180°,∴∠B=∠FDC.
∵CE⊥AB,CF⊥AD,∴∠CEB=∠F=90°.
在△CFD和△CEB中,
∴△CFD≌△CEB(AAS),∴CF=CE.
∵CE⊥AB,CF⊥AD,∴AC平分∠DAB.
(2)猜想:AB+AD=2AE.
证明:由(1)知△CFD≌△CEB,
∴CF=CE,DF=BE.
∵∠AEC=∠F=90°,AC=AC,
∴Rt△AEC≌Rt△AFC(HL),
∴AE=AF.
∵AB=AE+BE,AD=AF-DF=AE-BE,
∴AB+AD=2AE.
22.【解析】(1)∵∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE.
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,
∴∠BAC=∠DCE.
∵∠BAC=25°,
∴∠DCE=25°.
(2)①当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β.
②如图1,当点D在线段BC上时,α+β=180°;如图2,当点D在BC延长线或反向延长线上时,α=β.
2
