第十三章 轴对称 分层作业 (含答案)2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 第十三章 轴对称 分层作业 (含答案)2023-2024学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 343.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 21:55:47 | ||
图片预览


文档简介
第十三章 轴对称 自我评估
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.数学是一门重要的自然学科,同时也是一门精美的学科,数学之美有多种形式,比如数学图案,下列图形是以科学家名字命名的,其中是轴对称图形的有 ( )
A.赵爽弦图 B.斐波那契螺旋线
C.笛卡尔心形线 D.费马螺线曲线
2.等腰三角形一边的长为4 cm,周长是18 cm,则底边的长是 ( )
A.4 cm B.10 cm
C.7或10 cm D.4或10 cm
3.如图,在△ABC中,分别以A和B为圆心,相同的长大于AB为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知△CDE的面积比△CDB的面积小5,则△ADE的面积为 ( )
A.5 B.4 C.3 D.2
第3题图 第4题图
4.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论不正确的是 ( )
A.AD⊥BC B.EF=FD
C.BE=BD D.AE=AC
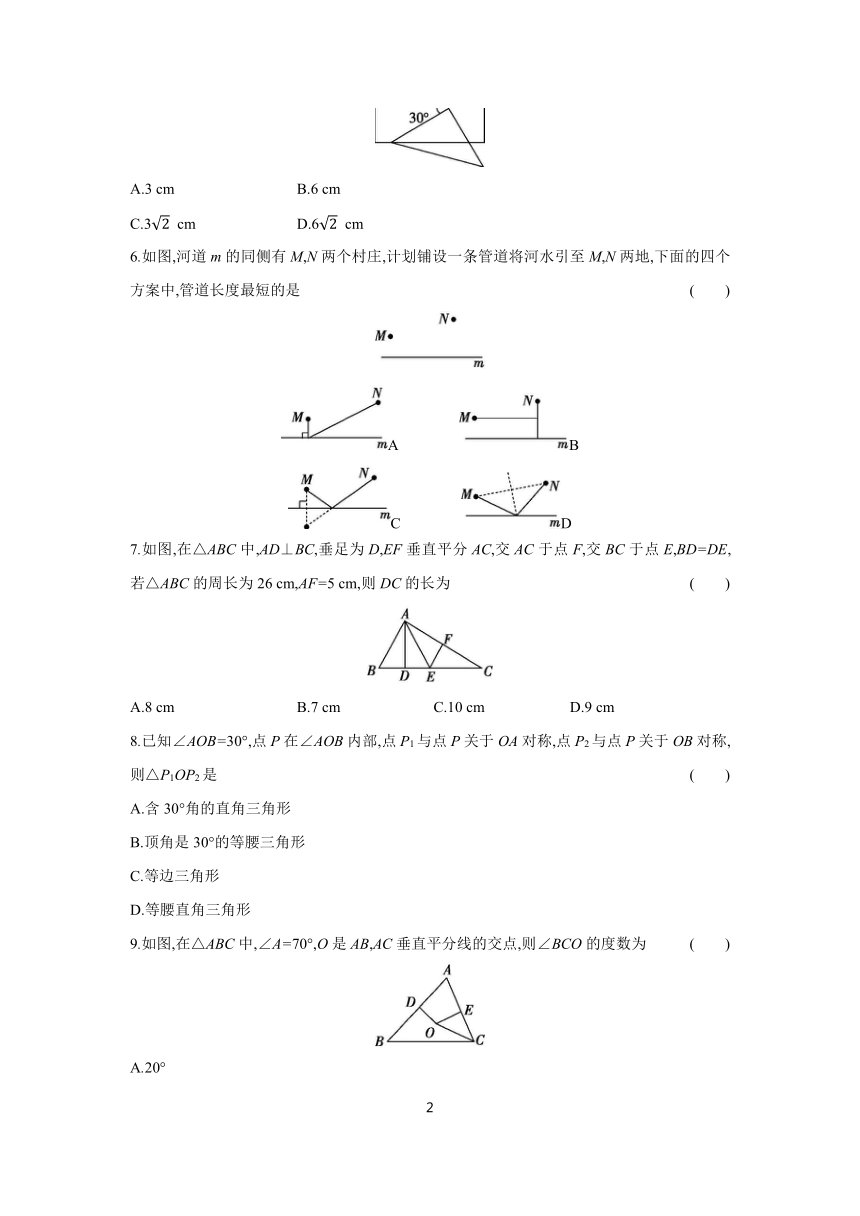
5.如图,将一个有45°角的直角三角板的直角顶点放在一张宽为3 cm的纸带边上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则三角板的直角边的长为 ( )
A.3 cm B.6 cm
C.3 cm D.6 cm
6.如图,河道m的同侧有M,N两个村庄,计划铺设一条管道将河水引至M,N两地,下面的四个方案中,管道长度最短的是 ( )
A B
C D
7.如图,在△ABC中,AD⊥BC,垂足为D,EF垂直平分AC,交AC于点F,交BC于点E,BD=DE,若△ABC的周长为26 cm,AF=5 cm,则DC的长为 ( )
A.8 cm B.7 cm C.10 cm D.9 cm
8.已知∠AOB=30°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,则△P1OP2是 ( )
A.含30°角的直角三角形
B.顶角是30°的等腰三角形
C.等边三角形
D.等腰直角三角形
9.如图,在△ABC中,∠A=70°,O是AB,AC垂直平分线的交点,则∠BCO的度数为 ( )
A.20°
B.30°
C.25°
D.35°
10.如图,一钢架BAC中,∠A=x°,焊上等长的钢条P1P2,P2P3,P3P4,P4P5,…来加固钢架,且P1A=P1P2,对于下列结论,判断正确的是 ( )
结论Ⅰ:若∠P3P2P4=75°,则x=25;
结论Ⅱ:若这样的钢条在钢架上至多能焊上6根,那么x的取值范围是≤x<15.
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对
C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
二、填空题(本大题共5小题,每小题3分,共15分)
11.已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2024的值为 .
12.如图,等腰三角形ABC底边BC的长为4 cm,面积是12 cm2,D为BC边上的中点,腰AB的垂直平分线EF交AD于点M,交AC于点F,则BM+DM的值为 cm.
13.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE为度数为 .
14.如图,有一轮船由东向西航行,在A处测得西偏北15°有一灯塔P.继续航行20海里后到B处,又测得灯塔P在西偏北30°.如果轮船航向不变,则灯塔与船之间的最近距离是 海里.
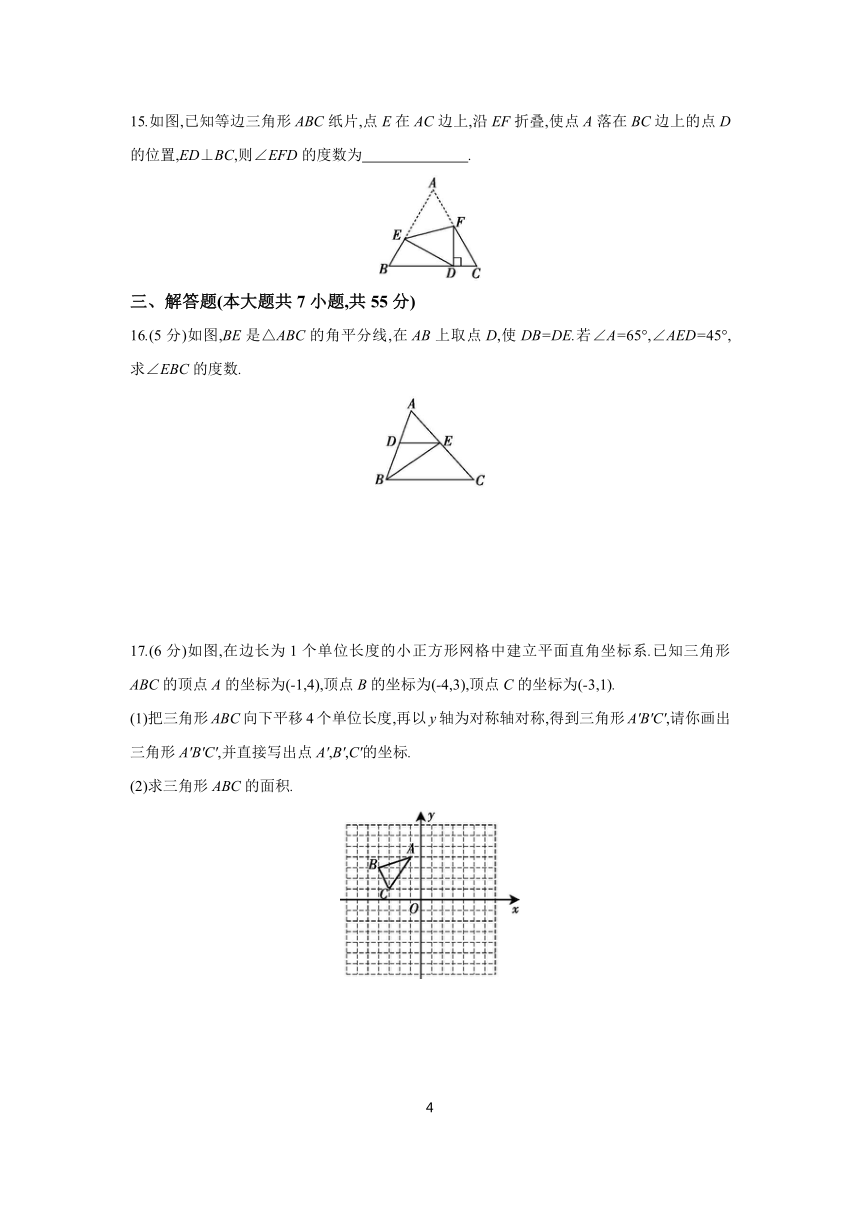
15.如图,已知等边三角形ABC纸片,点E在AC边上,沿EF折叠,使点A落在BC边上的点D的位置,ED⊥BC,则∠EFD的度数为 .
三、解答题(本大题共7小题,共55分)
16.(5分)如图,BE是△ABC的角平分线,在AB上取点D,使DB=DE.若∠A=65°,∠AED=45°,求∠EBC的度数.
17.(6分)如图,在边长为1个单位长度的小正方形网格中建立平面直角坐标系.已知三角形ABC的顶点A的坐标为(-1,4),顶点B的坐标为(-4,3),顶点C的坐标为(-3,1).
(1)把三角形ABC向下平移4个单位长度,再以y轴为对称轴对称,得到三角形A'B'C',请你画出三角形A'B'C',并直接写出点A',B',C'的坐标.
(2)求三角形ABC的面积.
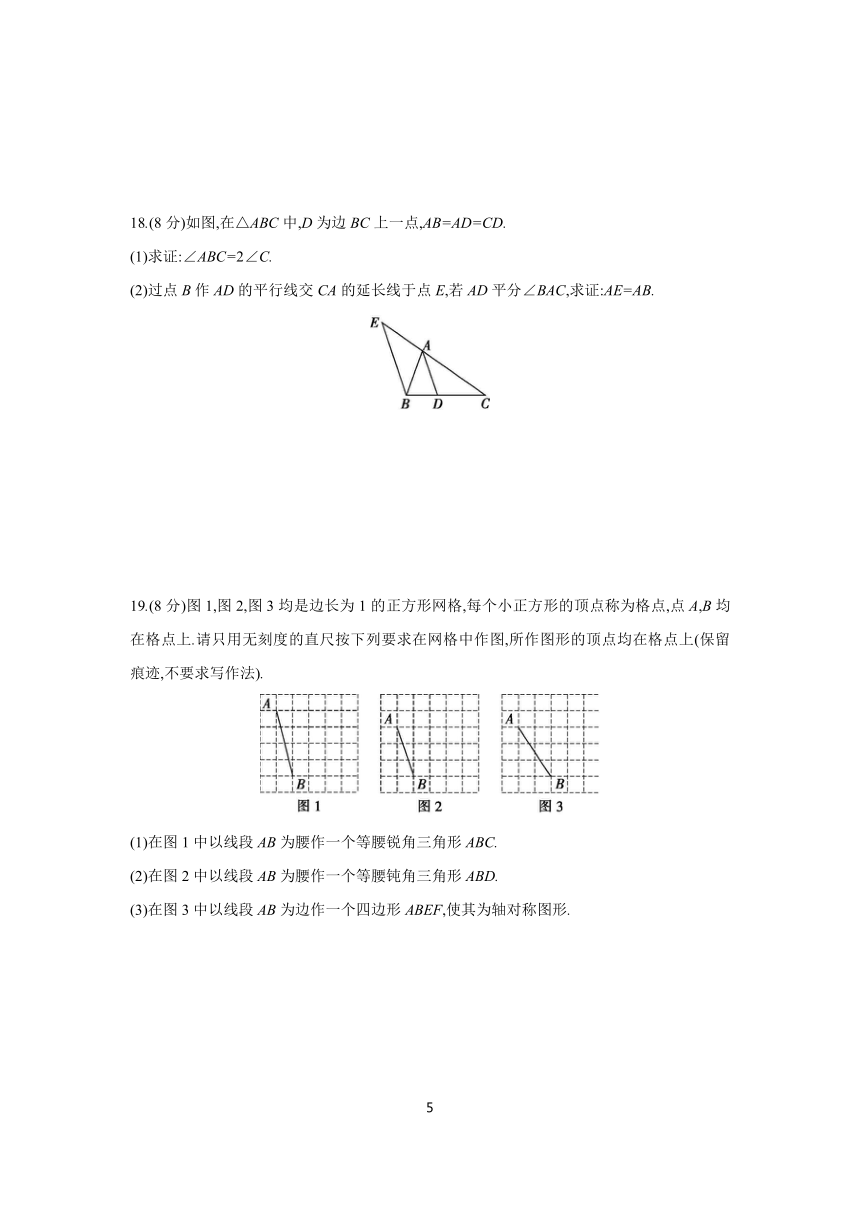
18.(8分)如图,在△ABC中,D为边BC上一点,AB=AD=CD.
(1)求证:∠ABC=2∠C.
(2)过点B作AD的平行线交CA的延长线于点E,若AD平分∠BAC,求证:AE=AB.
19.(8分)图1,图2,图3均是边长为1的正方形网格,每个小正方形的顶点称为格点,点A,B均在格点上.请只用无刻度的直尺按下列要求在网格中作图,所作图形的顶点均在格点上(保留痕迹,不要求写作法).
(1)在图1中以线段AB为腰作一个等腰锐角三角形ABC.
(2)在图2中以线段AB为腰作一个等腰钝角三角形ABD.
(3)在图3中以线段AB为边作一个四边形ABEF,使其为轴对称图形.
20.(8分)如图,在△ABC中,∠ABC=45°,P为边BC上一点,BC=3BP,且∠PAB=15°,点C关于直线PA的对称点为点D,连接BD,AH为△APC的PC边上的高.
(1)求∠BPD的大小.
(2)判断直线BD,AH是否平行 并说明理由.
21.(9分)如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C'的位置上.
(1)折叠后,DC的对应线段是 ,CF的对应线段是 .
(2)若∠1=50°,求∠2,∠3的度数.
(3)若AE=6,求CF的长度.
22.(11分)如图,在等边△ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形.
(2)若∠PAC=20°,求∠AEB的度数.
(3)连接CE,写出AE,BE,CE之间的数量关系,并证明你的结论.
参考答案
1.C 2.A 3.A 4.D 5.B 6.C 7.A 8.C 9.A
10.A
11.1
12.6
13.115°
14.10
15.45°
16.【解析】∵BE是△ABC的角平分线,∴∠DBE=∠CBE.
∵DB=DE,∴∠DBE=∠DEB,∴∠DEB=∠CBE,
∴DE∥BC,∴∠C=∠AED=45°.
在△ABC中,∠A+∠ABC+∠C=180°,
∴∠ABC=180°-∠A-∠C=180°-65°-45°=70°.
∵BE是△ABC的角平分线,
∴∠DBE=∠EBC=∠ABC=35°.
17.【解析】(1)如图,三角形A'B'C'为所求.
A'(1,0),B'(4,-1),C'(3,-3).
(2)三角形ABC的面积=3×3-×3×1-×2×1-×2×3=3.5.
18.【解析】证明:(1)∵AB=AD,∴∠ABC=∠ADB.
∵AD=CD,∴∠DAC=∠C.
∵∠ADB=∠DAC+∠C=2∠C,
∴∠ABC=2∠C.
(2)∵AD平分∠BAC,∴∠DAB=∠CAD.
∵BE∥AD,∴∠DAB=∠ABE,∠E=∠CAD,
∴∠ABE=∠E,∴AE=AB.
19.【解析】(1)如图1,等腰锐角三角形ABC即为所求(画法不唯一).
(2)如图2,等腰钝角三角形ABD即为所求.
(3)如图3,四边形ABEF即为所求.
20.【解析】(1)∵∠PAB=15°,∠ABC=45°,
∴∠APC=15°+45°=60°.
∵点C关于直线PA的对称点为点D,
∴PD=PC,AD=AC,
∴△ADP≌△ACP(SSS),∴∠APC=∠APD=60°,
∴∠BPD=180°-120°=60°.
(2)直线BD,AH平行.
理由:∵BC=3BP,∴BP=PC=PD,
如图,取PD中点E,连接BE,则△BEP为等边三角形,△BDE为等腰三角形,
∴∠BEP=60°,∴∠BDE=∠BEP=30°,
∴∠DBP=90°,即BD⊥BC.
又∵△APC的PC边上的高为AH,
∴AH⊥BC,∴BD∥AH.
21.【解析】(1)BC';C'F.
(2)∠2=50°,∠3=80°.
(3)在长方形ABCD中,根据折叠得BC'=DC,CF=C'F,∠C'=∠C,∠EBC'=∠D=90°,
∴∠ABC=∠EBC',∴∠ABE=∠C'BF.
又∵AB=DC=BC',∠A=∠C',
∴△ABE≌△C'BF(ASA),
∴C'F=AE,∴CF=C'F=AE=6.
22.【解析】(1)如图1所示.
(2)在等边△ABC中,AC=AB,∠BAC=60°,由对称可知:AC=AD,∠PAC=∠PAD,∴AB=AD,∴∠ABD=∠D.
∵∠PAC=20°,∴∠PAD=20°,∴∠BAD=∠BAC+∠PAC+∠PAD=100°,∴∠D=(180°-∠BAD)=40°,∴∠AEB=∠D+∠PAD=60°.
(3)CE+AE=BE.
证明:如图2,在BE上取点M使ME=AE,在等边△ABC中,AC=AB,∠BAC=60°,由对称可知:AC=AD,∠EAC=∠EAD,设∠EAC=∠DAE=x.∵AD=AC=AB,∴∠D=(180°-∠BAC-2x)=60°-x,∴∠AEB=∠D+∠CAE=60-x+x=60°,∴△AME为等边三角形.在△AEC和△AMB中,∴△AEC≌△AMB(SAS),
∴CE=BM,∴CE+AE=BE.
2
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.数学是一门重要的自然学科,同时也是一门精美的学科,数学之美有多种形式,比如数学图案,下列图形是以科学家名字命名的,其中是轴对称图形的有 ( )
A.赵爽弦图 B.斐波那契螺旋线
C.笛卡尔心形线 D.费马螺线曲线
2.等腰三角形一边的长为4 cm,周长是18 cm,则底边的长是 ( )
A.4 cm B.10 cm
C.7或10 cm D.4或10 cm
3.如图,在△ABC中,分别以A和B为圆心,相同的长大于AB为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知△CDE的面积比△CDB的面积小5,则△ADE的面积为 ( )
A.5 B.4 C.3 D.2
第3题图 第4题图
4.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论不正确的是 ( )
A.AD⊥BC B.EF=FD
C.BE=BD D.AE=AC
5.如图,将一个有45°角的直角三角板的直角顶点放在一张宽为3 cm的纸带边上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则三角板的直角边的长为 ( )
A.3 cm B.6 cm
C.3 cm D.6 cm
6.如图,河道m的同侧有M,N两个村庄,计划铺设一条管道将河水引至M,N两地,下面的四个方案中,管道长度最短的是 ( )
A B
C D
7.如图,在△ABC中,AD⊥BC,垂足为D,EF垂直平分AC,交AC于点F,交BC于点E,BD=DE,若△ABC的周长为26 cm,AF=5 cm,则DC的长为 ( )
A.8 cm B.7 cm C.10 cm D.9 cm
8.已知∠AOB=30°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,则△P1OP2是 ( )
A.含30°角的直角三角形
B.顶角是30°的等腰三角形
C.等边三角形
D.等腰直角三角形
9.如图,在△ABC中,∠A=70°,O是AB,AC垂直平分线的交点,则∠BCO的度数为 ( )
A.20°
B.30°
C.25°
D.35°
10.如图,一钢架BAC中,∠A=x°,焊上等长的钢条P1P2,P2P3,P3P4,P4P5,…来加固钢架,且P1A=P1P2,对于下列结论,判断正确的是 ( )
结论Ⅰ:若∠P3P2P4=75°,则x=25;
结论Ⅱ:若这样的钢条在钢架上至多能焊上6根,那么x的取值范围是≤x<15.
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对
C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
二、填空题(本大题共5小题,每小题3分,共15分)
11.已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2024的值为 .
12.如图,等腰三角形ABC底边BC的长为4 cm,面积是12 cm2,D为BC边上的中点,腰AB的垂直平分线EF交AD于点M,交AC于点F,则BM+DM的值为 cm.
13.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE为度数为 .
14.如图,有一轮船由东向西航行,在A处测得西偏北15°有一灯塔P.继续航行20海里后到B处,又测得灯塔P在西偏北30°.如果轮船航向不变,则灯塔与船之间的最近距离是 海里.
15.如图,已知等边三角形ABC纸片,点E在AC边上,沿EF折叠,使点A落在BC边上的点D的位置,ED⊥BC,则∠EFD的度数为 .
三、解答题(本大题共7小题,共55分)
16.(5分)如图,BE是△ABC的角平分线,在AB上取点D,使DB=DE.若∠A=65°,∠AED=45°,求∠EBC的度数.
17.(6分)如图,在边长为1个单位长度的小正方形网格中建立平面直角坐标系.已知三角形ABC的顶点A的坐标为(-1,4),顶点B的坐标为(-4,3),顶点C的坐标为(-3,1).
(1)把三角形ABC向下平移4个单位长度,再以y轴为对称轴对称,得到三角形A'B'C',请你画出三角形A'B'C',并直接写出点A',B',C'的坐标.
(2)求三角形ABC的面积.
18.(8分)如图,在△ABC中,D为边BC上一点,AB=AD=CD.
(1)求证:∠ABC=2∠C.
(2)过点B作AD的平行线交CA的延长线于点E,若AD平分∠BAC,求证:AE=AB.
19.(8分)图1,图2,图3均是边长为1的正方形网格,每个小正方形的顶点称为格点,点A,B均在格点上.请只用无刻度的直尺按下列要求在网格中作图,所作图形的顶点均在格点上(保留痕迹,不要求写作法).
(1)在图1中以线段AB为腰作一个等腰锐角三角形ABC.
(2)在图2中以线段AB为腰作一个等腰钝角三角形ABD.
(3)在图3中以线段AB为边作一个四边形ABEF,使其为轴对称图形.
20.(8分)如图,在△ABC中,∠ABC=45°,P为边BC上一点,BC=3BP,且∠PAB=15°,点C关于直线PA的对称点为点D,连接BD,AH为△APC的PC边上的高.
(1)求∠BPD的大小.
(2)判断直线BD,AH是否平行 并说明理由.
21.(9分)如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C'的位置上.
(1)折叠后,DC的对应线段是 ,CF的对应线段是 .
(2)若∠1=50°,求∠2,∠3的度数.
(3)若AE=6,求CF的长度.
22.(11分)如图,在等边△ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形.
(2)若∠PAC=20°,求∠AEB的度数.
(3)连接CE,写出AE,BE,CE之间的数量关系,并证明你的结论.
参考答案
1.C 2.A 3.A 4.D 5.B 6.C 7.A 8.C 9.A
10.A
11.1
12.6
13.115°
14.10
15.45°
16.【解析】∵BE是△ABC的角平分线,∴∠DBE=∠CBE.
∵DB=DE,∴∠DBE=∠DEB,∴∠DEB=∠CBE,
∴DE∥BC,∴∠C=∠AED=45°.
在△ABC中,∠A+∠ABC+∠C=180°,
∴∠ABC=180°-∠A-∠C=180°-65°-45°=70°.
∵BE是△ABC的角平分线,
∴∠DBE=∠EBC=∠ABC=35°.
17.【解析】(1)如图,三角形A'B'C'为所求.
A'(1,0),B'(4,-1),C'(3,-3).
(2)三角形ABC的面积=3×3-×3×1-×2×1-×2×3=3.5.
18.【解析】证明:(1)∵AB=AD,∴∠ABC=∠ADB.
∵AD=CD,∴∠DAC=∠C.
∵∠ADB=∠DAC+∠C=2∠C,
∴∠ABC=2∠C.
(2)∵AD平分∠BAC,∴∠DAB=∠CAD.
∵BE∥AD,∴∠DAB=∠ABE,∠E=∠CAD,
∴∠ABE=∠E,∴AE=AB.
19.【解析】(1)如图1,等腰锐角三角形ABC即为所求(画法不唯一).
(2)如图2,等腰钝角三角形ABD即为所求.
(3)如图3,四边形ABEF即为所求.
20.【解析】(1)∵∠PAB=15°,∠ABC=45°,
∴∠APC=15°+45°=60°.
∵点C关于直线PA的对称点为点D,
∴PD=PC,AD=AC,
∴△ADP≌△ACP(SSS),∴∠APC=∠APD=60°,
∴∠BPD=180°-120°=60°.
(2)直线BD,AH平行.
理由:∵BC=3BP,∴BP=PC=PD,
如图,取PD中点E,连接BE,则△BEP为等边三角形,△BDE为等腰三角形,
∴∠BEP=60°,∴∠BDE=∠BEP=30°,
∴∠DBP=90°,即BD⊥BC.
又∵△APC的PC边上的高为AH,
∴AH⊥BC,∴BD∥AH.
21.【解析】(1)BC';C'F.
(2)∠2=50°,∠3=80°.
(3)在长方形ABCD中,根据折叠得BC'=DC,CF=C'F,∠C'=∠C,∠EBC'=∠D=90°,
∴∠ABC=∠EBC',∴∠ABE=∠C'BF.
又∵AB=DC=BC',∠A=∠C',
∴△ABE≌△C'BF(ASA),
∴C'F=AE,∴CF=C'F=AE=6.
22.【解析】(1)如图1所示.
(2)在等边△ABC中,AC=AB,∠BAC=60°,由对称可知:AC=AD,∠PAC=∠PAD,∴AB=AD,∴∠ABD=∠D.
∵∠PAC=20°,∴∠PAD=20°,∴∠BAD=∠BAC+∠PAC+∠PAD=100°,∴∠D=(180°-∠BAD)=40°,∴∠AEB=∠D+∠PAD=60°.
(3)CE+AE=BE.
证明:如图2,在BE上取点M使ME=AE,在等边△ABC中,AC=AB,∠BAC=60°,由对称可知:AC=AD,∠EAC=∠EAD,设∠EAC=∠DAE=x.∵AD=AC=AB,∴∠D=(180°-∠BAC-2x)=60°-x,∴∠AEB=∠D+∠CAE=60-x+x=60°,∴△AME为等边三角形.在△AEC和△AMB中,∴△AEC≌△AMB(SAS),
∴CE=BM,∴CE+AE=BE.
2
