第十四章 整式的乘法与因式分解 分层作业(含答案) 2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 第十四章 整式的乘法与因式分解 分层作业(含答案) 2023-2024学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 125.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 23:00:09 | ||
图片预览



文档简介
第十四章 整式的乘法与因式分解 自我评估
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.若a·2×23=28,则a等于 ( )
A.4 B.8 C.16 D.32
2.下列运算中的结果为a3的是 ( )
A.a+a2 B.a6+a2 C.a·a2 D.(-a)3
3.墨迹覆盖了等式“a3■a3=a6(a≠0)”中的运算符号,则覆盖的是 ( )
A.+ B.- C.× D.÷
4.若3n+3n+3n=36,则n= ( )
A.2 B.3 C.4 D.5
5.下列计算正确的是 ( )
A.2a+3a=5a2
B.(a2)3=a5
C.(a+1)2=a2+1
D.(a+2)(a-2)=a2-4
6.下列各式分解因式正确的是 ( )
A.x2+6xy+9y2=(x+3y)2
B.2x2-4xy+9y2=(2x-3y)2
C.2x2-8y2=2(x+4y)(x-4y)
D.x(x-y)+y(y-x)=(x-y)(x+y)
7.算式(5×3n)(5×3n)可以写成 ( )
A.5×32n B.25×32n C.5×92n D.25×92n
8.一位密码编译爱好者,在他的密码手册中有这样一条信息:a-b,x-1,3,x2+1,a,x+1分别对应下列六个字:国,爱,我,数,学,祖,现将3a(x2-1)-3b(x2-1)因式分解,结果呈现的密码信息可能是 ( )
A.爱数学 B.我爱数学
C.爱祖国 D.我爱祖国
9.一个长方体的长、宽、高分别是3x-4、2x-1和x,则它的体积是 ( )
A.6x3-5x2+4x B.6x3-11x2+4x
C.6x3-4x2 D.6x3-4x2+x+4
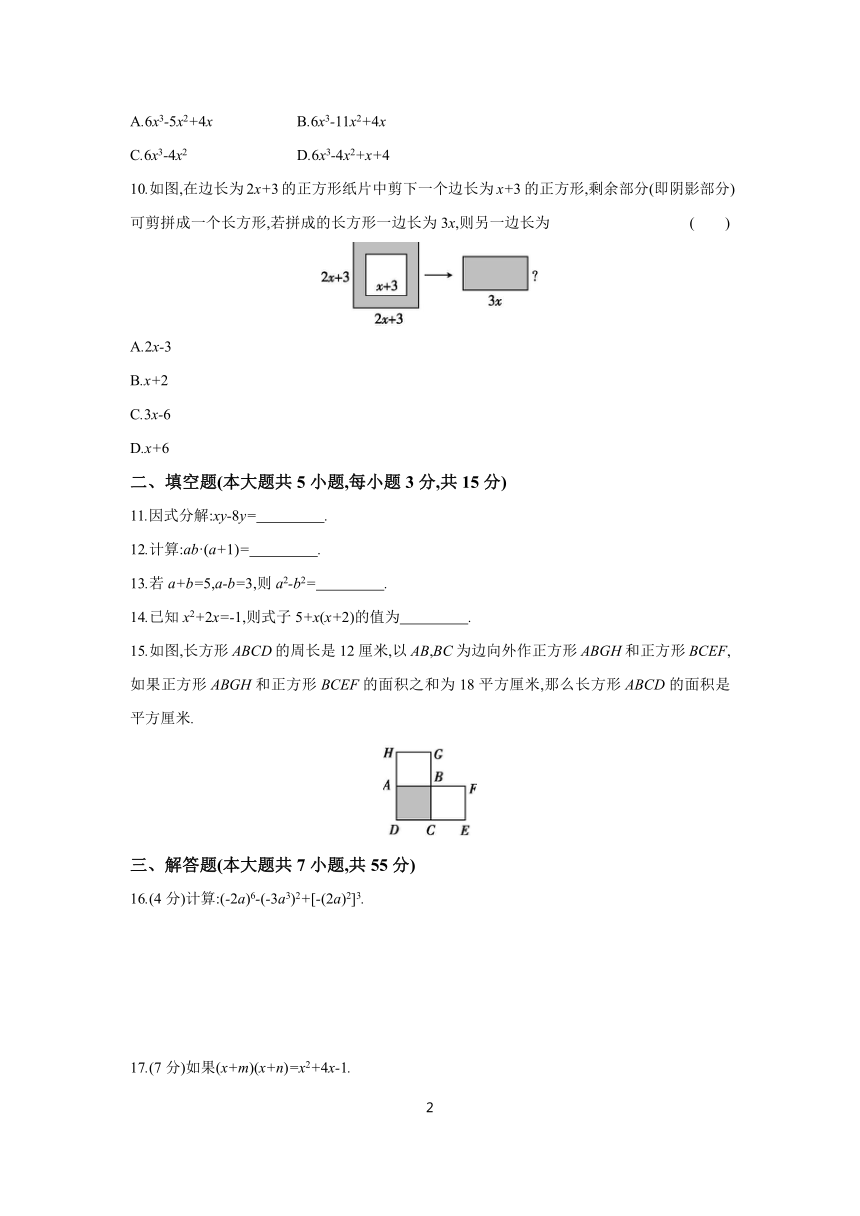
10.如图,在边长为2x+3的正方形纸片中剪下一个边长为x+3的正方形,剩余部分(即阴影部分)可剪拼成一个长方形,若拼成的长方形一边长为3x,则另一边长为 ( )
A.2x-3
B.x+2
C.3x-6
D.x+6
二、填空题(本大题共5小题,每小题3分,共15分)
11.因式分解:xy-8y= .
12.计算:ab·(a+1)= .
13.若a+b=5,a-b=3,则a2-b2= .
14.已知x2+2x=-1,则式子5+x(x+2)的值为 .
15.如图,长方形ABCD的周长是12厘米,以AB,BC为边向外作正方形ABGH和正方形BCEF,如果正方形ABGH和正方形BCEF的面积之和为18平方厘米,那么长方形ABCD的面积是 平方厘米.
三、解答题(本大题共7小题,共55分)
16.(4分)计算:(-2a)6-(-3a3)2+[-(2a)2]3.
17.(7分)如果(x+m)(x+n)=x2+4x-1.
(1)填空:m+n= ,mn= .
(2)根据(1)的结果,求下列式子的值:
①m2+5mn+n2;
②(m-n)2.
18.(7分)若x+y=2,且(x+3)(y+3)=12.
(1)求xy的值.
(2)求x2+3xy+y2的值.
19.(8分)小亮在课余时间写了三个算式:32-12=8×1,52-32=8×2,72-52=8×3,通过认真观察,发现任意两个连续奇数的平方差是8的倍数.
(1)92-72的结果是8的几倍
(2)设两个连续奇数为2n+1,2n-1(其中n为正整数),试证明它们的平方差是8的倍数.
(3)直接写出两个连续偶数的平方差是几的倍数.
20.(8分)从边长为a的正方形中减掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 .
(2)运用你从(1)写出的等式,完成下列各题:
①已知:a-b=3,a2-b2=21,求a+b的值;
②计算:1-×1-×1-×…×1-×1-.
21.(9分)“杨辉三角”揭示了(a+b)n(n为非负数)展开式的各项系数的规律.在欧洲,这个表叫做帕斯卡三角形,帕斯卡是在1654年发现这一规律的,比杨辉要迟393年,比贾宪迟600年.请仔细观察“杨辉三角”中每个数字与上一行的左右两个数字之和的关系.
根据上述规律,完成下列各题:
(1)将(a+b)5展开后,各项的系数和为 .
(2)将(a+b)n展开后,各项的系数和为 .
(3)(a+b)6= .
22.(12分)如图,有足够多的边长为a的小正方形(A类),宽为a、长为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图1中的三类图形可以拼出一些长方形来解释某些等式.
(1)用图1中的若干个图形(三类图形都要用到)拼成一个正方形,使其面积为(a+b)2,画出图形,并根据图形回答(a+b)2= .
(2)图2是由图1中的三类图形拼出的一个长方形,根据图2可以得到并解释等式: .
(3)用图1中的若干个图形(三类图形都要用到)拼成一个长方形,使其面积为a2+4ab+3b2,写出你的拼法,并根据你画的图形分解因式:a2+4ab+3b2.
参考答案
1.C 2.C 3.C 4.D 5.D 6.A 7.B 8.D 9.B
10.B
11.y(x-8)
12.a2b+ab
13.15
14.4
15.9
16.【解析】原式=(-2)6·a6-(-3)2·(a3)2+(-1)3·(2a)6
=64a6-9a6-64a6
=-9a6.
17.【解析】(1)4;-1.
提示:∵(x+m)(x+n)=x2+(m+n)x+mn=x2+4x-1,
∴m+n=4,mn=-1.
(2)①m2+5mn+n2=(m+n)2+3mn=42+3×(-1)=16-3=13.
②(m-n)2=(m+n)2-4mn=42-4×(-1)=16+4=20.
18.【解析】(1)∵(x+3)(y+3)=12,
∴xy+3x+3y+9=12,
则xy+3(x+y)=3.
将x+y=2代入得xy+6=3,
则xy=-3.
(2)当xy=-3,x+y=2时,
原式=(x+y)2+xy
=22+(-3)
=4-3
=1.
19.【解析】(1)92-72=81-49=32,32是8的4倍.
(2)(2n+1)2-(2n-1)2=(2n+1-2n+1)(2n+1+2n-1)=2×4n=8n,
故两个连续奇数的平方差是8的倍数.
82-62=64-36=28,
(3)两个连续偶数的平方差是4的倍数.
20.【解析】(1)a2-b2=(a+b)(a-b).
提示:图1阴影部分的面积为a2-b2,图2阴影部分的面积为(a+b)(a-b),二者相等,从而能验证的等式为a2-b2=(a+b)(a-b).
(2)①∵a-b=3,a2-b2=21,a2-b2=(a+b)(a-b),
∴21=(a+b)×3,
∴a+b=7.
②1-×1-×1-×…×1-×1-
=1-×1+×1-×1+×1-×1+…1-×1+×1-×1+
=××××××…××××
=×
=.
21.【解析】(1)32.(2)2n.
(3)a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6.
22.【解析】(1)如图1所示.
(a+b)(a+b)=(a+b)2=a2+2ab+b2,
即(a+b)2=a2+2ab+b2.
故答案为a2+2ab+b2.
(2)由题图2可知,长方形的面积为(a+2b)(2a+b),还可以写成2a2+5ab+2b2,
∴(a+2b)(2a+b)=2a2+5ab+2b2.
故答案为(a+2b)(2a+b)=2a2+5ab+2b2.
(3)如图2所示,
长方形的长为a+3b,宽为a+b,面积为(a+3b)(a+b)=a2+4ab+3b2,
即a2+4ab+3b2=(a+3b)(a+b).
2
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.若a·2×23=28,则a等于 ( )
A.4 B.8 C.16 D.32
2.下列运算中的结果为a3的是 ( )
A.a+a2 B.a6+a2 C.a·a2 D.(-a)3
3.墨迹覆盖了等式“a3■a3=a6(a≠0)”中的运算符号,则覆盖的是 ( )
A.+ B.- C.× D.÷
4.若3n+3n+3n=36,则n= ( )
A.2 B.3 C.4 D.5
5.下列计算正确的是 ( )
A.2a+3a=5a2
B.(a2)3=a5
C.(a+1)2=a2+1
D.(a+2)(a-2)=a2-4
6.下列各式分解因式正确的是 ( )
A.x2+6xy+9y2=(x+3y)2
B.2x2-4xy+9y2=(2x-3y)2
C.2x2-8y2=2(x+4y)(x-4y)
D.x(x-y)+y(y-x)=(x-y)(x+y)
7.算式(5×3n)(5×3n)可以写成 ( )
A.5×32n B.25×32n C.5×92n D.25×92n
8.一位密码编译爱好者,在他的密码手册中有这样一条信息:a-b,x-1,3,x2+1,a,x+1分别对应下列六个字:国,爱,我,数,学,祖,现将3a(x2-1)-3b(x2-1)因式分解,结果呈现的密码信息可能是 ( )
A.爱数学 B.我爱数学
C.爱祖国 D.我爱祖国
9.一个长方体的长、宽、高分别是3x-4、2x-1和x,则它的体积是 ( )
A.6x3-5x2+4x B.6x3-11x2+4x
C.6x3-4x2 D.6x3-4x2+x+4
10.如图,在边长为2x+3的正方形纸片中剪下一个边长为x+3的正方形,剩余部分(即阴影部分)可剪拼成一个长方形,若拼成的长方形一边长为3x,则另一边长为 ( )
A.2x-3
B.x+2
C.3x-6
D.x+6
二、填空题(本大题共5小题,每小题3分,共15分)
11.因式分解:xy-8y= .
12.计算:ab·(a+1)= .
13.若a+b=5,a-b=3,则a2-b2= .
14.已知x2+2x=-1,则式子5+x(x+2)的值为 .
15.如图,长方形ABCD的周长是12厘米,以AB,BC为边向外作正方形ABGH和正方形BCEF,如果正方形ABGH和正方形BCEF的面积之和为18平方厘米,那么长方形ABCD的面积是 平方厘米.
三、解答题(本大题共7小题,共55分)
16.(4分)计算:(-2a)6-(-3a3)2+[-(2a)2]3.
17.(7分)如果(x+m)(x+n)=x2+4x-1.
(1)填空:m+n= ,mn= .
(2)根据(1)的结果,求下列式子的值:
①m2+5mn+n2;
②(m-n)2.
18.(7分)若x+y=2,且(x+3)(y+3)=12.
(1)求xy的值.
(2)求x2+3xy+y2的值.
19.(8分)小亮在课余时间写了三个算式:32-12=8×1,52-32=8×2,72-52=8×3,通过认真观察,发现任意两个连续奇数的平方差是8的倍数.
(1)92-72的结果是8的几倍
(2)设两个连续奇数为2n+1,2n-1(其中n为正整数),试证明它们的平方差是8的倍数.
(3)直接写出两个连续偶数的平方差是几的倍数.
20.(8分)从边长为a的正方形中减掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 .
(2)运用你从(1)写出的等式,完成下列各题:
①已知:a-b=3,a2-b2=21,求a+b的值;
②计算:1-×1-×1-×…×1-×1-.
21.(9分)“杨辉三角”揭示了(a+b)n(n为非负数)展开式的各项系数的规律.在欧洲,这个表叫做帕斯卡三角形,帕斯卡是在1654年发现这一规律的,比杨辉要迟393年,比贾宪迟600年.请仔细观察“杨辉三角”中每个数字与上一行的左右两个数字之和的关系.
根据上述规律,完成下列各题:
(1)将(a+b)5展开后,各项的系数和为 .
(2)将(a+b)n展开后,各项的系数和为 .
(3)(a+b)6= .
22.(12分)如图,有足够多的边长为a的小正方形(A类),宽为a、长为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图1中的三类图形可以拼出一些长方形来解释某些等式.
(1)用图1中的若干个图形(三类图形都要用到)拼成一个正方形,使其面积为(a+b)2,画出图形,并根据图形回答(a+b)2= .
(2)图2是由图1中的三类图形拼出的一个长方形,根据图2可以得到并解释等式: .
(3)用图1中的若干个图形(三类图形都要用到)拼成一个长方形,使其面积为a2+4ab+3b2,写出你的拼法,并根据你画的图形分解因式:a2+4ab+3b2.
参考答案
1.C 2.C 3.C 4.D 5.D 6.A 7.B 8.D 9.B
10.B
11.y(x-8)
12.a2b+ab
13.15
14.4
15.9
16.【解析】原式=(-2)6·a6-(-3)2·(a3)2+(-1)3·(2a)6
=64a6-9a6-64a6
=-9a6.
17.【解析】(1)4;-1.
提示:∵(x+m)(x+n)=x2+(m+n)x+mn=x2+4x-1,
∴m+n=4,mn=-1.
(2)①m2+5mn+n2=(m+n)2+3mn=42+3×(-1)=16-3=13.
②(m-n)2=(m+n)2-4mn=42-4×(-1)=16+4=20.
18.【解析】(1)∵(x+3)(y+3)=12,
∴xy+3x+3y+9=12,
则xy+3(x+y)=3.
将x+y=2代入得xy+6=3,
则xy=-3.
(2)当xy=-3,x+y=2时,
原式=(x+y)2+xy
=22+(-3)
=4-3
=1.
19.【解析】(1)92-72=81-49=32,32是8的4倍.
(2)(2n+1)2-(2n-1)2=(2n+1-2n+1)(2n+1+2n-1)=2×4n=8n,
故两个连续奇数的平方差是8的倍数.
82-62=64-36=28,
(3)两个连续偶数的平方差是4的倍数.
20.【解析】(1)a2-b2=(a+b)(a-b).
提示:图1阴影部分的面积为a2-b2,图2阴影部分的面积为(a+b)(a-b),二者相等,从而能验证的等式为a2-b2=(a+b)(a-b).
(2)①∵a-b=3,a2-b2=21,a2-b2=(a+b)(a-b),
∴21=(a+b)×3,
∴a+b=7.
②1-×1-×1-×…×1-×1-
=1-×1+×1-×1+×1-×1+…1-×1+×1-×1+
=××××××…××××
=×
=.
21.【解析】(1)32.(2)2n.
(3)a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6.
22.【解析】(1)如图1所示.
(a+b)(a+b)=(a+b)2=a2+2ab+b2,
即(a+b)2=a2+2ab+b2.
故答案为a2+2ab+b2.
(2)由题图2可知,长方形的面积为(a+2b)(2a+b),还可以写成2a2+5ab+2b2,
∴(a+2b)(2a+b)=2a2+5ab+2b2.
故答案为(a+2b)(2a+b)=2a2+5ab+2b2.
(3)如图2所示,
长方形的长为a+3b,宽为a+b,面积为(a+3b)(a+b)=a2+4ab+3b2,
即a2+4ab+3b2=(a+3b)(a+b).
2
