第十一章 三角形 分层作业 (含答案)2023-2024学年数学人教版八年级上册
文档属性
| 名称 | 第十一章 三角形 分层作业 (含答案)2023-2024学年数学人教版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 203.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 00:00:00 | ||
图片预览



文档简介
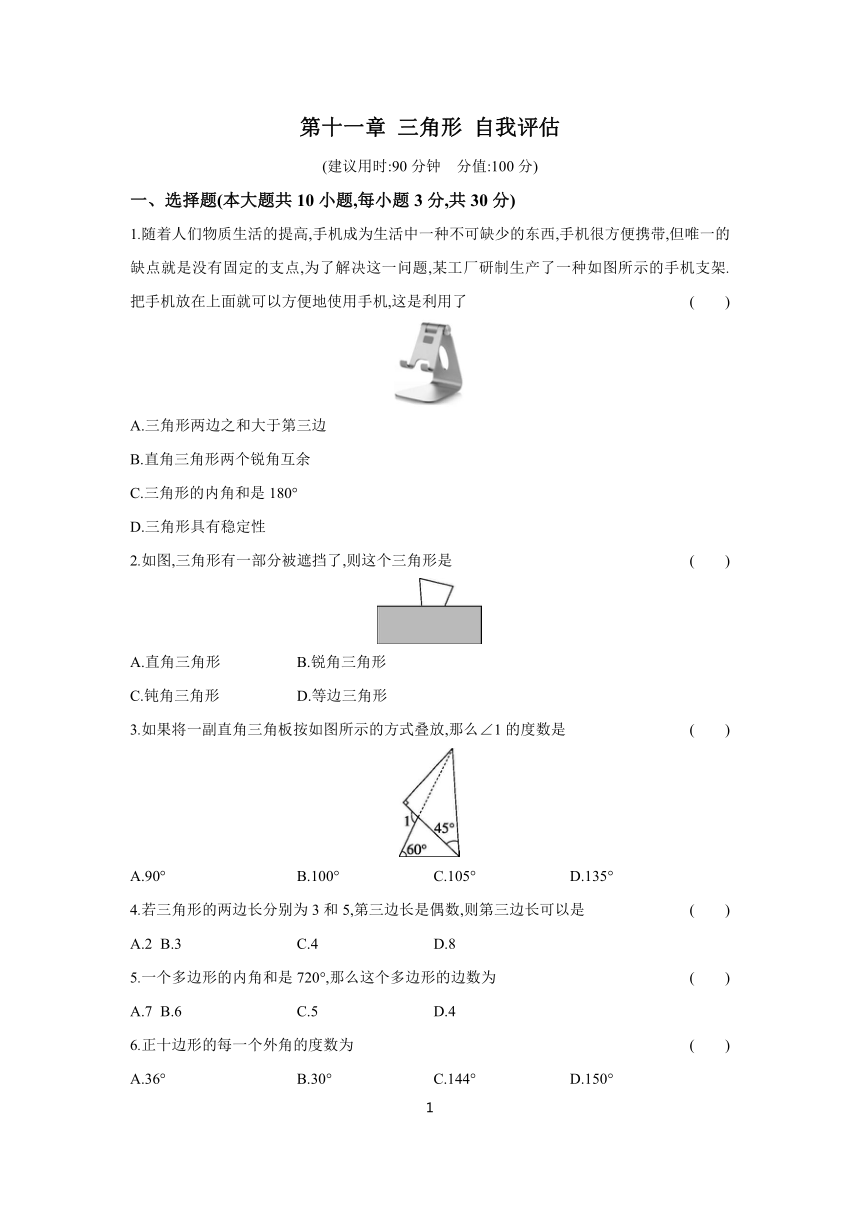
第十一章 三角形 自我评估
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.随着人们物质生活的提高,手机成为生活中一种不可缺少的东西,手机很方便携带,但唯一的缺点就是没有固定的支点,为了解决这一问题,某工厂研制生产了一种如图所示的手机支架.把手机放在上面就可以方便地使用手机,这是利用了 ( )
A.三角形两边之和大于第三边
B.直角三角形两个锐角互余
C.三角形的内角和是180°
D.三角形具有稳定性
2.如图,三角形有一部分被遮挡了,则这个三角形是 ( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
3.如果将一副直角三角板按如图所示的方式叠放,那么∠1的度数是 ( )
A.90° B.100° C.105° D.135°
4.若三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是 ( )
A.2 B.3 C.4 D.8
5.一个多边形的内角和是720°,那么这个多边形的边数为 ( )
A.7 B.6 C.5 D.4
6.正十边形的每一个外角的度数为 ( )
A.36° B.30° C.144° D.150°
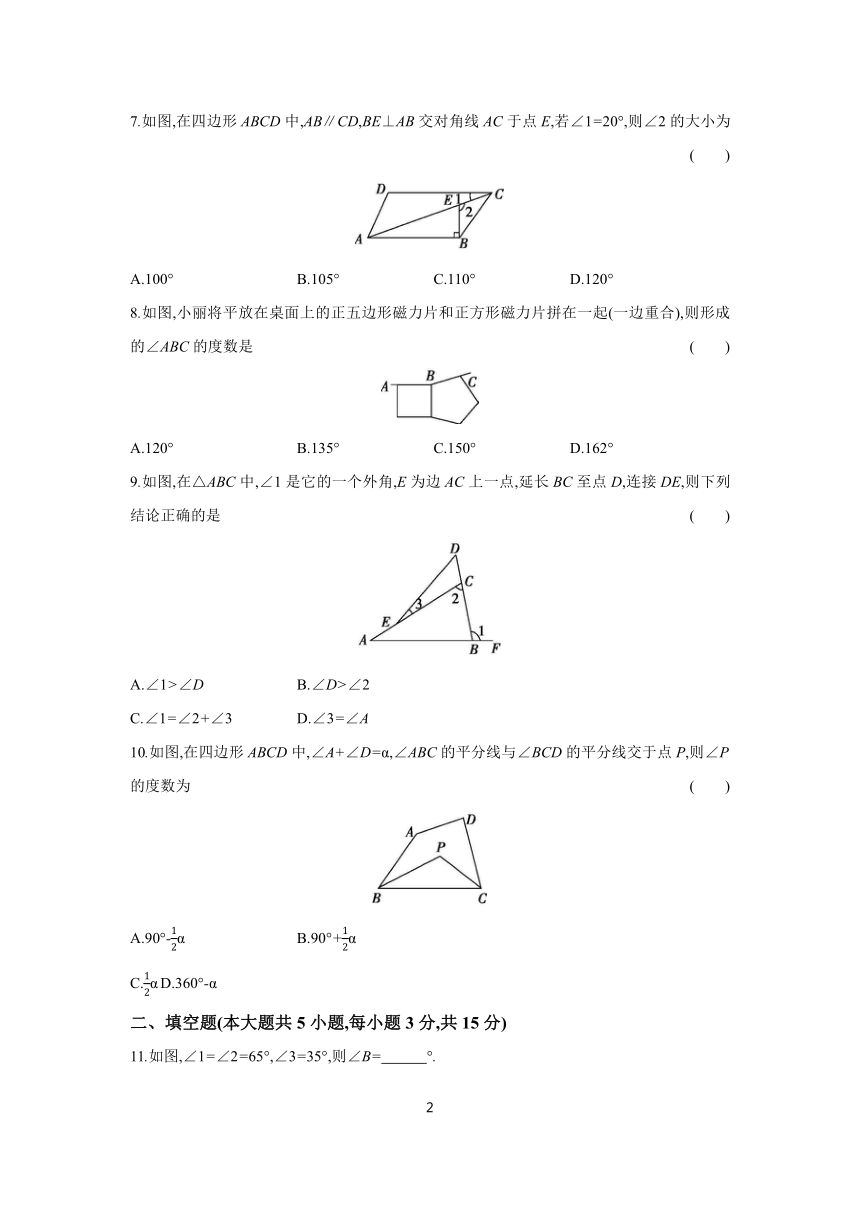
7.如图,在四边形ABCD中,AB∥CD,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的大小为 ( )
A.100° B.105° C.110° D.120°
8.如图,小丽将平放在桌面上的正五边形磁力片和正方形磁力片拼在一起(一边重合),则形成的∠ABC的度数是 ( )
A.120° B.135° C.150° D.162°
9.如图,在△ABC中,∠1是它的一个外角,E为边AC上一点,延长BC至点D,连接DE,则下列结论正确的是 ( )
A.∠1>∠D B.∠D>∠2
C.∠1=∠2+∠3 D.∠3=∠A
10.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P的度数为 ( )
A.90°-α B.90°+α
C.α D.360°-α
二、填空题(本大题共5小题,每小题3分,共15分)
11.如图,∠1=∠2=65°,∠3=35°,则∠B= °.
12.如图,点A的坐标为(3,2),点B的坐标为(5,0),则△ABO的面积是 .
13.如图,BD是△ABC的中线,E是BD的中点,若S△ABE+S△BCD=6,则△ABC的面积是 .
14.如图,在四边形ABCD中,∠DAB的平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=260°,则∠P= °.
15.如图,∠O=30°,任意裁剪的直角三角形纸板两条直角边所在直线与∠O的两边分别交于D,E两点.
请从A,B两题中任选一题作答,我选择 题.
A.如图1,若直角顶点C在∠O内部,则∠ADO+∠OEB= .
B.如图2,如果直角顶点C在∠O外部,则∠ADO+∠OEB= .
三、解答题(本大题共7小题,共55分)
16.(5分)如图,求x和y的值.
17.(6分)如图,AD是△ABC的中线.
(1)作出△ACD的边CD上的高.
(2)若△ACD的面积为6,且边CD上的高为3,求BC的长.
18.(6分)如图,点A在点B的北偏东40°方向,点C在点B的北偏东75°方向,点A在点C的北偏西50°方向,
(1)求证:△ABC是直角三角形.
(2)求∠ACB的度数.
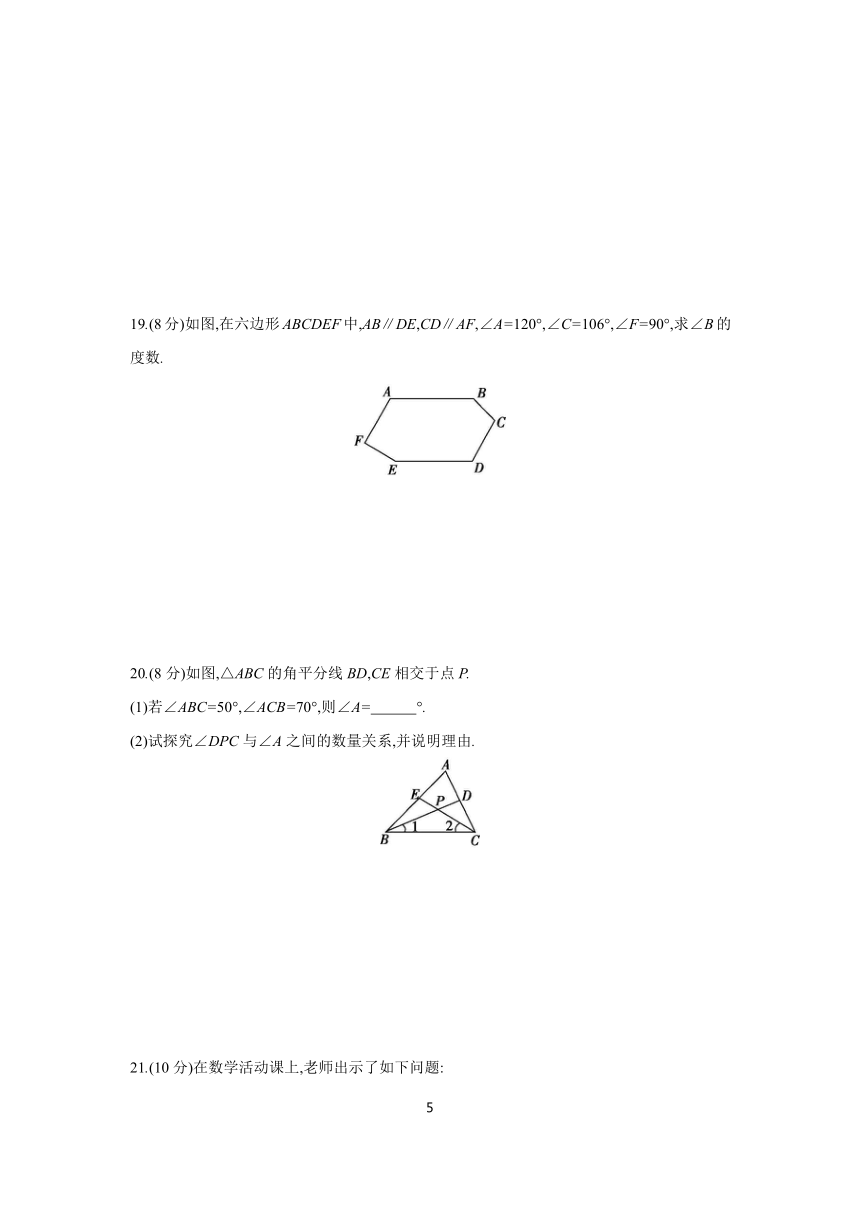
19.(8分)如图,在六边形ABCDEF中,AB∥DE,CD∥AF,∠A=120°,∠C=106°,∠F=90°,求∠B的度数.
20.(8分)如图,△ABC的角平分线BD,CE相交于点P.
(1)若∠ABC=50°,∠ACB=70°,则∠A= °.
(2)试探究∠DPC与∠A之间的数量关系,并说明理由.
21.(10分)在数学活动课上,老师出示了如下问题:
如图1,已知直线AB∥CD,将三角形纸片EFG的顶点E放到直线AB上,点F落在直线AB与CD所夹区域的内部,FG与CD交于点H,试探究∠EFH,∠BEF,∠DHF之间的数量关系.“兴趣小组”有如下探究思路:
过点F作FT∥AB.∵AB∥CD,∴FT∥CD,
∴∠BEF=∠TFE,…
数学思考
(1)请你根据“兴趣小组”的探究思路,直接写出∠EFH,∠BEF,∠DHF之间的数量关系: .
问题解决
(2)“智慧小组”把老师提出的问题作了如下变式:将三角形纸片EFG按图2所示的方式放置,使得点F落在直线AB的上方,FG与AB,CD分别交于点M,H.试探究∠EFH,∠BEF,∠DHF之间的数量关系.
请你类比“兴趣小组”的探究思路,解决“智慧小组”提出的问题.
结论运用
(3)如图3,直线AB∥CD,∠PND=75°,∠EPF=35°,∠PQM=95°.请你运用问题(1),(2)中得到的结论,求∠QMC的度数.
22.(12分)已知∠MON=40°,OE平分∠MON,A,B,C分别是射线OM,OE,ON上的动点(A,B,C不与点O重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则
①∠ABO的度数是 .
②当∠BAD=∠ABD时,x= ;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角 若存在,求出x的值;若不存在,说明理由.
参考答案
1.D 2.B 3.C 4.C 5.B 6.A 7.C 8.D 9.A
10.C
11.30
12.5
13.8
14.40
15.A.120°
B.120°
16.【解析】由三角形的外角性质可知,x+70=x+x+10,
解得x=60,
因此y=180-(60+70)=50.
17.【解析】(1)如图,AE为边CD上的高.
(2)由×3CD=6,得CD=4.
∵AD是△ABC的中线,
∴BC=2CD=8.
18.【解析】(1)证明:如图,过点A作AD∥BE.
∵点A在点B的北偏东40°方向,点A在点C的北偏西50°方向,
∴∠DAB=∠ABE=40°,∠CAD=∠ACF=50°,
∴∠BAC=∠BAD+∠CAD=40°+50°=90°,
∴△ABC是直角三角形.
(2)∠ABC=∠EBC-∠ABE=75°-40°=35°.
∵△ABC是直角三角形,
∴∠ACB=90°-∠ABC=90°-35°=55°.
19.【解析】如图,延长AF,DE交于点G.
∵AB∥DE,
∴∠G=180°-∠A=180°-120°=60°.
∵CD∥AF,
∴∠D=180°-∠G=180°-60°=120°.
在五边形ABCDG中,∠A+∠B+∠C+∠D+∠G=(5-2)×180°=540°,
∴∠B=540°-120°-106°-120°-60°=134°.
20.【解析】(1)60.
提示:在△ABC中,∠ABC+∠ACB+∠A=180°,
∴∠A=180°-∠ABC-∠ACB=180°-50°-70°=60°.
(2)∠DPC=90°-∠A.理由如下:
∵∠ABC,∠ACB的平分线相交于点P,
∴∠1=∠ABC,∠2=∠ACB,
∴∠BPC=180°-∠1-∠2=180°-∠ABC-∠ACB=180°-(∠ABC+∠ACB).
又∵∠ABC+∠ACB=180°-∠A,
∴∠BPC=180°-(180°-∠A)=90°+∠A,
∴∠DPC=180°-∠BPC=90°-∠A.
21.【解析】(1)∠EFH=∠BEF+∠DHF.
(2)∵AB∥CD,
∴∠FMB=∠DHF.
∵∠FMB=∠EFH+∠BEF,
∴∠DHF=∠EFH+∠BEF.
(3)由(2)可知,∠PND=∠BEP+∠EPF.
∵∠PND=75°,∠EPF=35°,
∴∠PEF=∠PND-∠EPF=75°-35°=40°,
∴∠AEQ=∠PEF=40°.
由(1)可知,∠PQM=∠AEQ+∠QMC,
∵∠PQM=95°,∴∠QMC=∠PQM-∠AEQ=95°-40°=55°.
22.【解析】(1)①20°.②120;60.
(2)①当点D在线段OB上时,若∠BAD=∠ABD,则x=20.若∠BAD=∠BDA,则x=35.若∠ADB=∠ABD,则x=50.
②当点D在射线BE上时,因为∠ABE=110°,且三角形的内角和为180°,
所以只有∠BAD=∠BDA,此时x=125.
综上可知,存在这样的x的值,使得△ADB中有两个相等的角,且x=20或35或50或125.
2
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.随着人们物质生活的提高,手机成为生活中一种不可缺少的东西,手机很方便携带,但唯一的缺点就是没有固定的支点,为了解决这一问题,某工厂研制生产了一种如图所示的手机支架.把手机放在上面就可以方便地使用手机,这是利用了 ( )
A.三角形两边之和大于第三边
B.直角三角形两个锐角互余
C.三角形的内角和是180°
D.三角形具有稳定性
2.如图,三角形有一部分被遮挡了,则这个三角形是 ( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
3.如果将一副直角三角板按如图所示的方式叠放,那么∠1的度数是 ( )
A.90° B.100° C.105° D.135°
4.若三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是 ( )
A.2 B.3 C.4 D.8
5.一个多边形的内角和是720°,那么这个多边形的边数为 ( )
A.7 B.6 C.5 D.4
6.正十边形的每一个外角的度数为 ( )
A.36° B.30° C.144° D.150°
7.如图,在四边形ABCD中,AB∥CD,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的大小为 ( )
A.100° B.105° C.110° D.120°
8.如图,小丽将平放在桌面上的正五边形磁力片和正方形磁力片拼在一起(一边重合),则形成的∠ABC的度数是 ( )
A.120° B.135° C.150° D.162°
9.如图,在△ABC中,∠1是它的一个外角,E为边AC上一点,延长BC至点D,连接DE,则下列结论正确的是 ( )
A.∠1>∠D B.∠D>∠2
C.∠1=∠2+∠3 D.∠3=∠A
10.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P的度数为 ( )
A.90°-α B.90°+α
C.α D.360°-α
二、填空题(本大题共5小题,每小题3分,共15分)
11.如图,∠1=∠2=65°,∠3=35°,则∠B= °.
12.如图,点A的坐标为(3,2),点B的坐标为(5,0),则△ABO的面积是 .
13.如图,BD是△ABC的中线,E是BD的中点,若S△ABE+S△BCD=6,则△ABC的面积是 .
14.如图,在四边形ABCD中,∠DAB的平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=260°,则∠P= °.
15.如图,∠O=30°,任意裁剪的直角三角形纸板两条直角边所在直线与∠O的两边分别交于D,E两点.
请从A,B两题中任选一题作答,我选择 题.
A.如图1,若直角顶点C在∠O内部,则∠ADO+∠OEB= .
B.如图2,如果直角顶点C在∠O外部,则∠ADO+∠OEB= .
三、解答题(本大题共7小题,共55分)
16.(5分)如图,求x和y的值.
17.(6分)如图,AD是△ABC的中线.
(1)作出△ACD的边CD上的高.
(2)若△ACD的面积为6,且边CD上的高为3,求BC的长.
18.(6分)如图,点A在点B的北偏东40°方向,点C在点B的北偏东75°方向,点A在点C的北偏西50°方向,
(1)求证:△ABC是直角三角形.
(2)求∠ACB的度数.
19.(8分)如图,在六边形ABCDEF中,AB∥DE,CD∥AF,∠A=120°,∠C=106°,∠F=90°,求∠B的度数.
20.(8分)如图,△ABC的角平分线BD,CE相交于点P.
(1)若∠ABC=50°,∠ACB=70°,则∠A= °.
(2)试探究∠DPC与∠A之间的数量关系,并说明理由.
21.(10分)在数学活动课上,老师出示了如下问题:
如图1,已知直线AB∥CD,将三角形纸片EFG的顶点E放到直线AB上,点F落在直线AB与CD所夹区域的内部,FG与CD交于点H,试探究∠EFH,∠BEF,∠DHF之间的数量关系.“兴趣小组”有如下探究思路:
过点F作FT∥AB.∵AB∥CD,∴FT∥CD,
∴∠BEF=∠TFE,…
数学思考
(1)请你根据“兴趣小组”的探究思路,直接写出∠EFH,∠BEF,∠DHF之间的数量关系: .
问题解决
(2)“智慧小组”把老师提出的问题作了如下变式:将三角形纸片EFG按图2所示的方式放置,使得点F落在直线AB的上方,FG与AB,CD分别交于点M,H.试探究∠EFH,∠BEF,∠DHF之间的数量关系.
请你类比“兴趣小组”的探究思路,解决“智慧小组”提出的问题.
结论运用
(3)如图3,直线AB∥CD,∠PND=75°,∠EPF=35°,∠PQM=95°.请你运用问题(1),(2)中得到的结论,求∠QMC的度数.
22.(12分)已知∠MON=40°,OE平分∠MON,A,B,C分别是射线OM,OE,ON上的动点(A,B,C不与点O重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则
①∠ABO的度数是 .
②当∠BAD=∠ABD时,x= ;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角 若存在,求出x的值;若不存在,说明理由.
参考答案
1.D 2.B 3.C 4.C 5.B 6.A 7.C 8.D 9.A
10.C
11.30
12.5
13.8
14.40
15.A.120°
B.120°
16.【解析】由三角形的外角性质可知,x+70=x+x+10,
解得x=60,
因此y=180-(60+70)=50.
17.【解析】(1)如图,AE为边CD上的高.
(2)由×3CD=6,得CD=4.
∵AD是△ABC的中线,
∴BC=2CD=8.
18.【解析】(1)证明:如图,过点A作AD∥BE.
∵点A在点B的北偏东40°方向,点A在点C的北偏西50°方向,
∴∠DAB=∠ABE=40°,∠CAD=∠ACF=50°,
∴∠BAC=∠BAD+∠CAD=40°+50°=90°,
∴△ABC是直角三角形.
(2)∠ABC=∠EBC-∠ABE=75°-40°=35°.
∵△ABC是直角三角形,
∴∠ACB=90°-∠ABC=90°-35°=55°.
19.【解析】如图,延长AF,DE交于点G.
∵AB∥DE,
∴∠G=180°-∠A=180°-120°=60°.
∵CD∥AF,
∴∠D=180°-∠G=180°-60°=120°.
在五边形ABCDG中,∠A+∠B+∠C+∠D+∠G=(5-2)×180°=540°,
∴∠B=540°-120°-106°-120°-60°=134°.
20.【解析】(1)60.
提示:在△ABC中,∠ABC+∠ACB+∠A=180°,
∴∠A=180°-∠ABC-∠ACB=180°-50°-70°=60°.
(2)∠DPC=90°-∠A.理由如下:
∵∠ABC,∠ACB的平分线相交于点P,
∴∠1=∠ABC,∠2=∠ACB,
∴∠BPC=180°-∠1-∠2=180°-∠ABC-∠ACB=180°-(∠ABC+∠ACB).
又∵∠ABC+∠ACB=180°-∠A,
∴∠BPC=180°-(180°-∠A)=90°+∠A,
∴∠DPC=180°-∠BPC=90°-∠A.
21.【解析】(1)∠EFH=∠BEF+∠DHF.
(2)∵AB∥CD,
∴∠FMB=∠DHF.
∵∠FMB=∠EFH+∠BEF,
∴∠DHF=∠EFH+∠BEF.
(3)由(2)可知,∠PND=∠BEP+∠EPF.
∵∠PND=75°,∠EPF=35°,
∴∠PEF=∠PND-∠EPF=75°-35°=40°,
∴∠AEQ=∠PEF=40°.
由(1)可知,∠PQM=∠AEQ+∠QMC,
∵∠PQM=95°,∴∠QMC=∠PQM-∠AEQ=95°-40°=55°.
22.【解析】(1)①20°.②120;60.
(2)①当点D在线段OB上时,若∠BAD=∠ABD,则x=20.若∠BAD=∠BDA,则x=35.若∠ADB=∠ABD,则x=50.
②当点D在射线BE上时,因为∠ABE=110°,且三角形的内角和为180°,
所以只有∠BAD=∠BDA,此时x=125.
综上可知,存在这样的x的值,使得△ADB中有两个相等的角,且x=20或35或50或125.
2
