人教版七年级下册 第5章 相交线与平行线 单元测试卷 (含解析)
文档属性
| 名称 | 人教版七年级下册 第5章 相交线与平行线 单元测试卷 (含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 388.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 00:00:00 | ||
图片预览




文档简介
人教版七年级下册 第5章 相交线与平行线 单元测试卷
一.选择题(共12小题,满分36分,每小题3分)
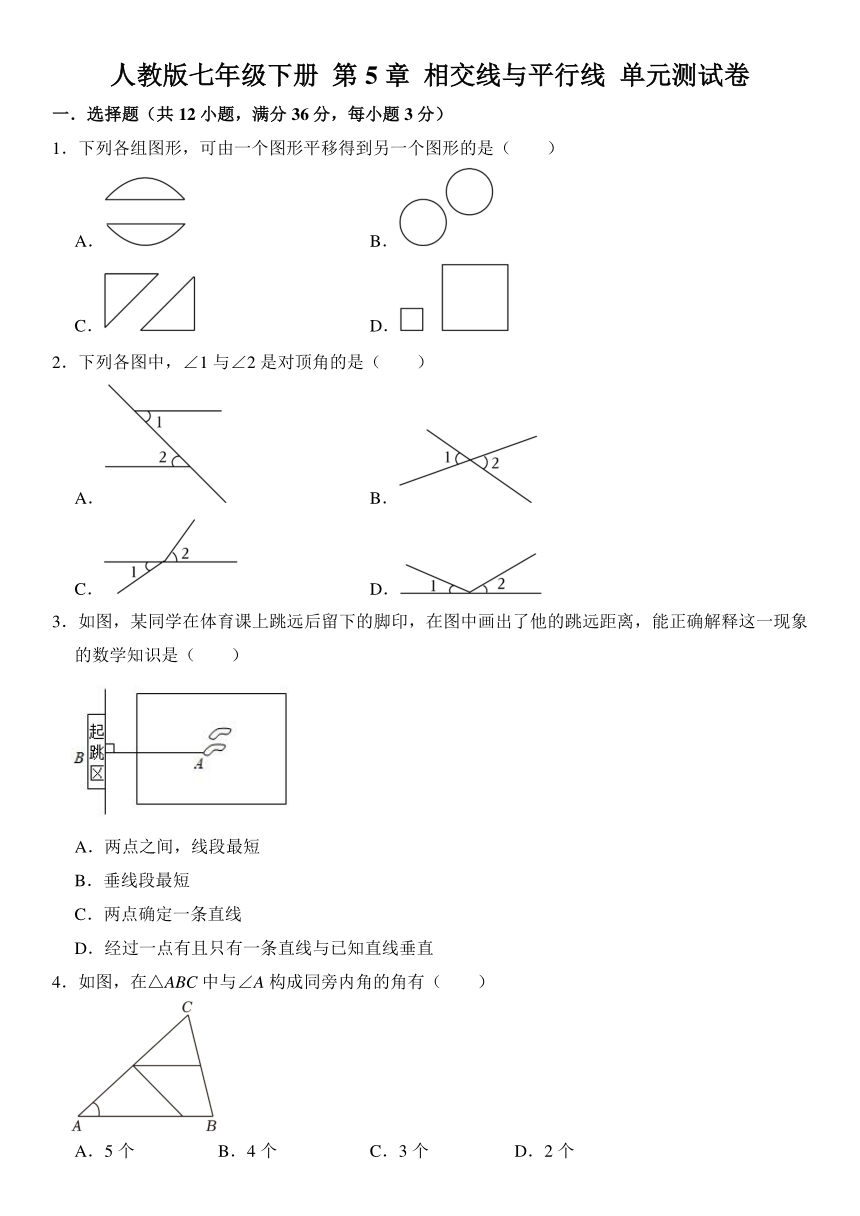
1.下列各组图形,可由一个图形平移得到另一个图形的是( )
A. B.
C. D.
2.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
3.如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.经过一点有且只有一条直线与已知直线垂直
4.如图,在△ABC中与∠A构成同旁内角的角有( )
A.5个 B.4个 C.3个 D.2个
5.下列命题中,是假命题的是( )
A.两点之间,线段最短 B.同旁内角互补
C.等角的补角相等 D.垂线段最短
6.下列说法正确的是( )
A.经过已知一点有且只有一条直线与已知直线平行
B.两个相等的角是对顶角
C.互补的两个角一定是邻补角
D.直线外一点与直线上各点连接的所有线段中,垂线段最短
7.如图所示,直线AB,CD相交于点O,OE⊥OF,OF平分∠BOD,∠BOF:∠BOC=1:4,则∠BOE的度数为( )
A.45° B.55° C.60° D.65°
8.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠D=∠DCE D.∠D+∠ACD=180°
9.如图,直线AB,CD被直线CE所截,AB∥CD,∠1=140°,则∠C的度数为( )
A.30° B.40° C.50° D.60°
10.观察下列图形,并阅读图形下面的相关文字,如图所示:两条直线相交,最多有一个交点,三条直线相交,最多有三个交点,四条直线相交,最多有6个交点,像这样,10条直线相交,最多交点的个数是( )
A.40个 B.45个 C.50个 D.55个
11.如图,△ABC平移到△DEF的位置,则下列说法:①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C到点F的方向;④平移距离为线段BD的长.其中说法正确的有( )
A.①② B.①③ C.①④ D.②④
12.如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P,点F为焦点.若∠1=x°,∠2=y°,则∠3 的度数为( )
A.(x﹣y)° B.(180﹣x﹣y)°
C.(180﹣x+y)° D.(x+y﹣90)°
二.填空题(共6小题,满分18分,每小题3分)
13.如图,直线a,b相交于点O.如果∠1+∠2=60°,那么∠3的度数为 .
14.将命题“同角的余角相等”,改写成“如果…,那么…”的形式 .
15.在同一平面内,如果直线a⊥b,直线b⊥c,则a与c的位置关系是 .
16.如图,AB∥CD,BC∥DE,∠B=72°,则∠D= 度.
17.如图所示,某商场重新装修后,准备在门前台阶上铺设地毯,已知这种地毯的批发价为每平方米40元,其台阶的尺寸如图所示,则购买地毯至少需要 元.
18.将一副三角板中的两块直角三角尺按如图方式放置(其中∠ABC=45°,∠D=60°),固定三角尺ABC,将三角尺BDE以每秒30°的速度绕点B按逆时针方向旋转180°停止.在这个过程中,当运动时间为 秒时,三角尺BDE的一边与三角尺ABC的某一边平行(不共线).
三.解答题(共6小题,满分46分)
19.(6分)已知:如图,∠ABD=∠D,BD平分∠ABC.求证:AD∥BC.
20.(7分)如图,直线AB,CD相交于点O,OM⊥AB于点O.
(1)若∠1=∠2,求∠NOD的度数;
(2)若∠BOC=4∠1,求∠AOC,∠MOD的度数.
21.(8分)如图,直线AB∥CD,∠1=70°,∠D=110°,求∠B的度数.
阅读下面的解答过程,并填空(理由或数学式).
解:∵AB∥CD(已知),
∴∠1=(① )(② ).
又∵∠1=70°,∠D=110°(已知),
∴∠1+∠D=180°(等式的性质).
∴∠C+∠D=180°(③ ).
∴(④ )∥(⑤ )(⑥ ).
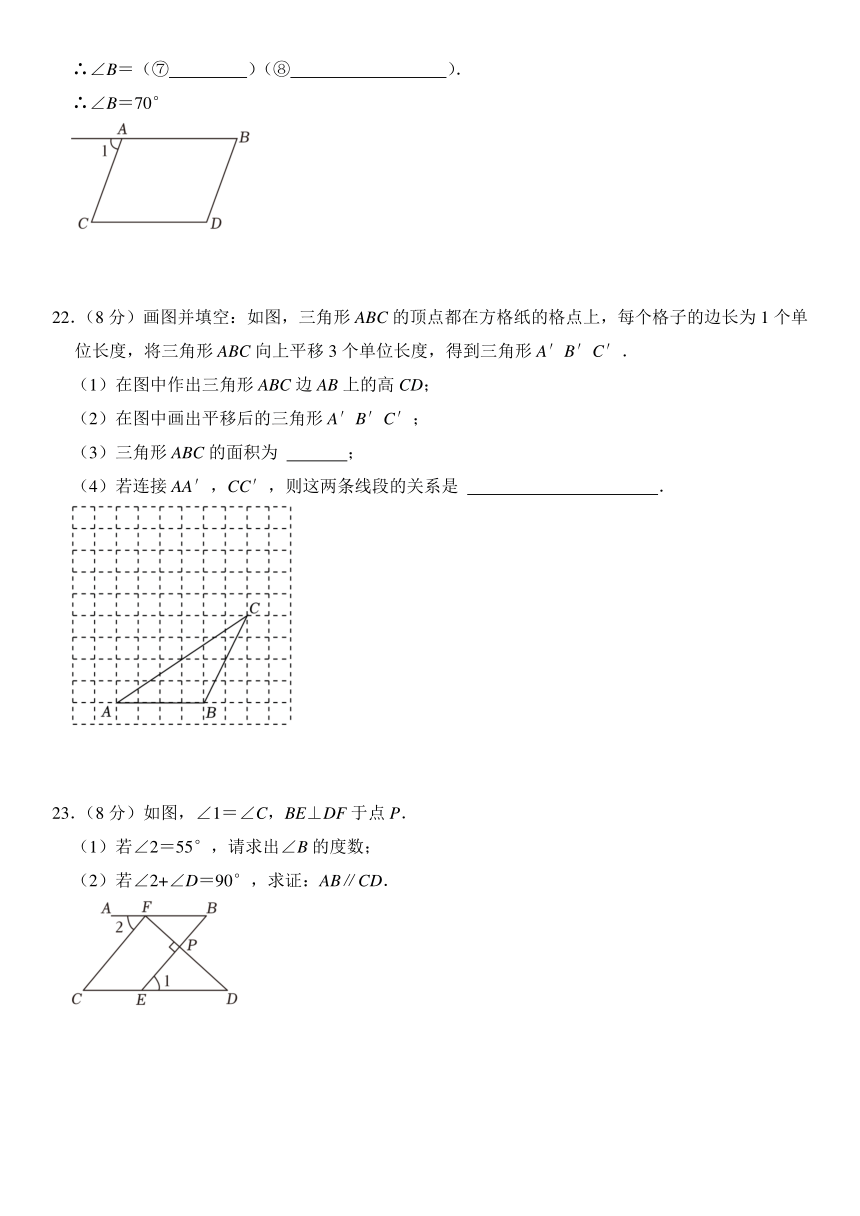
∴∠B=(⑦ )(⑧ ).
∴∠B=70°
22.(8分)画图并填空:如图,三角形ABC的顶点都在方格纸的格点上,每个格子的边长为1个单位长度,将三角形ABC向上平移3个单位长度,得到三角形A′B′C′.
(1)在图中作出三角形ABC边AB上的高CD;
(2)在图中画出平移后的三角形A′B′C′;
(3)三角形ABC的面积为 ;
(4)若连接AA′,CC′,则这两条线段的关系是 .
23.(8分)如图,∠1=∠C,BE⊥DF于点P.
(1)若∠2=55°,请求出∠B的度数;
(2)若∠2+∠D=90°,求证:AB∥CD.
24.(9分)已知,如图AB∥CD,AF平分∠EAB,DF平分∠EDC.
(1)如图1,探究∠F与∠E的数量关系并证明.
(2)如图2,在(1)的条件下,过A作AH∥ED交DC于点H,AD平分∠EAH,∠DAG:∠FDE=2:7,求∠BAH的度数.
参考答案
一.选择题(共12小题,满分36分,每小题3分)
1.解:A、图形由轴对称所得到,不属于平移,故本选项不符合题意;
B、图形平移前后的形状和大小没有变化,只是位置发生变化,符合平移性质,故本选项符合题意;
C、图形由旋转所得到,不属于平移,故本选项不符合题意;
D、图形大小不一,大小发生变化,不符合平移性质,故本选项不符合题意.
故选:B.
2.解:由对顶角的定义可知,选项B中的∠1与∠2是对顶角,
故选:B.
3.解:如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是垂线段最短.
故选:B.
4.解:在△ABC中与∠A构成同旁内角的角有∠ADE,∠ADF,∠AED,∠C,∠B,共5个.
故选:A.
5.解:A、两点之间,线段最短,是真命题;
B、两直线平行,同旁内角互补,原命题是假命题;
C、等角的补角相等,是真命题;
D、垂线段最短,是真命题;
故选:B.
6.解:A、应为在同一平面内,经过直线外一点有且只有一条直线与已知直线平行,故本选项错误;
B、对顶角相等,但相等的两个角不一定是对顶角,故本选项错误;
C、邻补角互补,但互补的两个角不一定是邻补角,故本选项错误;
D、直线外一点与直线上各点连接的所有线段中,垂线段最短,故本选项正确.
故选:D.
7.解:∵∠BOF:∠BOC=1:4,
∴设∠BOF=x°,则∠BOC=4x°,
∵OF平分∠BOD,
∴∠BOF=∠DOF=x°,
∵∠BOC+∠BOF+∠DOF=180°,
∴4x+x+x=180,
解得:x=30,
∴∠BOF=30°,
∵OE⊥OF,
∴∠EOF=90°,
∴∠BOE=∠EOF﹣∠BOF=60°,
故选:C.
8.解:A.根据内错角相等,两直线平行即可证得AB∥CD;
B.根据内错角相等,两直线平行即可证得BD∥AC,不能证AB∥CD;
C.根据内错角相等,两直线平行即可证得BD∥AC,不能证AB∥CD;
D.根据同旁内角互补,两直线平行,即可证得BD∥AC,不能证AB∥CD.
故选:A.
9.解:∵∠1=140°,
∴∠AEC=180°﹣140°=40°,
∵AB∥CD,
∴∠C=∠AEC=40°.
故选:B.
10.解:2条直线相交,最多有1个交点,即0+1=1(个),
3条直线相交,最多有3个交点,即1+2=3(个),
4条直线相交,最多有6个交点,即1+2+3=6(个),
5条直线相交,最多有10个交点,即1+2+3+4=10(个),
…
10条直线相交,最多有45个交点,即1+2+3+4+5+6+7+8+9=45(个),
故选:B.
11.解:由平移的性质可知,
①AB∥DE,AD=CF=BE,因此正确;
②由平移的性质可知,∠ACB=∠DFE,因此②不正确;
③平移的方向是点C到点F的方向或点A到点D的方向或点B到点E的方向,因此正确;
④平移距离为线段BE或线段AD或线段CF的长,因此④不正确;
综上所述,正确的结论有:①③,
故选:B.
12.解:由题意可知AB∥OF.
∴∠1+∠OFB=180°.
∵∠1=x°.
∴∠OFB=180°﹣x°.
∵∠2=∠POF.
∴∠3=∠POF+∠OFB=(180﹣x+y)°.
故选:C.
二.填空题
13.解:∵∠1+∠2=60°,∠1=∠2(对顶角相等),
∴∠1=∠2=30°,
∵∠1与∠3互为邻补角,
∴∠3=180°﹣∠1=180°﹣30°=150°.
故答案为:150.
14.解:命题“同角的余角相等”,可以改写成:如果两个角是同一个角的余角,那么这两个角相等.
故答案为如果两个角是同一个角的余角,那么这两个角相等.
15.解:如图,
∵a⊥b,
∴∠1=90°,
∵b⊥c,
∴∠2=90°,
∴∠1=∠2,
∴a∥c,
故答案为:a∥c.
16.解:∵AB∥CD,∠B=72°,
∴∠C=∠B=72°,
∵BC∥DE,
∴∠D=180°﹣∠C=180°﹣72°=108°.
故答案为:108.
17.解:利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为1.6米,0.8米,
∴地毯的长度为1.6+0.8=2.4(米),地毯的面积为2.4×2=4.8(平方米),
∴购买地毯至少需要4.8×40=192(元).
故答案为:192.
18.解:当DE∥AB时,如图1,
此时∠ABE=∠E=30°,
∴∠CBE=15°,
t=15°÷30°=0.5;
当BD∥AC时,如图2,
此时∠DBC=45°,
t=45°÷30°=1.5;
当DE∥AC时,如图3,
此时,∠EBC=60°+45°=105°,
t=105°÷30°=3.5;
当BE∥AC时,如图4,
此时∠EBC=90°+45°=135°,
∴t=135°÷30°=4.5;
当DE∥BC时,如图5,
此时∠EBC=90°+60°=150°,
t=150°÷30°=5,
故答案为:0.5或1.5或3.5或4.5或5.
三.解答题
19.证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠ABD=∠D,
∴∠CBD=∠D,
∴AD∥BC.
20.解:(1)∵OM⊥AB,
∴∠AOM=90°,
∴∠AOC+∠1=90°,
∵∠1=∠2,
∴∠AOC+∠2=90°,即∠NOC=90°,
∴∠NOD=180°﹣∠NOC=90°.
∴∠NOD的度数为90°;
(2)∵OM⊥AB,
∴∠BOM=90°,
∵∠BOC=4∠1,
∴∠BOM+∠1=4∠1,即90°+∠1=4∠1,
解得∠1=30°,
∴∠AOC=90°﹣30°=60°,∠MOD=180°﹣∠1=150°.
∴∠AOC的度数为60°,∠MOD的度数为150°.
21.解:∵AB∥CD(已知),
∴∠1=∠C(两直线平行,内错角相等).
又∵∠1=70°,∠D=110°(已知),
∴∠1+∠D=180°(等式的性质).
∴∠C+∠D=180° (等量代换),
∴AC∥BD(同旁内角互补,两直线平行),
∴∠B=∠1(两直线平行,同位角相等),
∴∠B=70°,
故答案为:∠C;两直线平行,内错角相等;等量代换;AC;BD;同旁内角互补,两直线平行;∠1;两直线平行,同位角相等.
22.解:(1)如图,线段CD即为所求;
(2)如图,△A′B′C′即为所求;
(3)S△ABC=AB CD=×4×4=8,
故答案为:8;
(4)AA′=CC′,AA′∥CC′,
故答案为:AA′=CC′,AA′∥CC′.
23.(1)解:∵∠1=∠C(已知),
∴BE∥CF(同位角相等,两直线平行),
∴∠B=∠2=55°(两直线平行,同位角相等);
(2)证明:∵BE⊥DF(已知),
∴∠DPE=90°(垂直定义),
∵BE∥CF(已证),
∴∠CFD=∠DPE=90°(两直线平行,同位角相等),
∴∠2+∠BFD=180﹣∠CFD=90°(平角定义),
∵∠2+∠D=90°(已知),
∴∠BFD=∠D(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
24.(1)2∠AFD+∠AED=360°,
证明:如图,过点E作EM∥AB,过点F作FN∥AB,
∵FN∥AB,
∴∠NFA=∠BAF,
∵AF平分∠EAB,
∴∠EAB=2∠BAF,
∴∠EAB=2∠NAF,
∵FN∥AB,AB∥CD,
∴FN∥CD,
∴∠NFD=∠FDC,
∵DF平分∠EDC,
∴∠EDC=2∠FDC,
∴∠EDC=2∠NFD,
∴∠BAE+∠EDC=2(∠NFA+∠NFD)=2∠AFD,
∵AB∥CD,
∴EM∥CD,
∵EM∥AB,
∴∠BAE+∠AEM=180°,
∵EM∥CD,
∴∠DEM+∠EDC=180°,
∴(∠BAE+∠AEM)+(∠DEM+∠EDC)=360°,
即∠BAE+∠AED+∠EDC=360°,
∴∠AED=360°﹣(∠EAB+∠EDC)=360°﹣2∠AFD,
2∠AFD+∠AED=360°;
(2)解:∵∠DAG:∠FDE=2:7,
∴设∠DAG=2α,∠FDE=∠FDG=7α,
∴∠EDH=2∠FDG=14α,
∵∠GAD=∠GAE﹣∠DAE=∠BAE﹣∠EAH=∠BAH,
∴∠BAH=4α,
∵AB∥CD,
∴∠AHD=∠BAH=4α,
∵AH∥ED,
∴∠AHD+∠EDH=180°,
∴4α+14α=180°,
解得:α=10°,
∴∠BAH=4α=40°.
一.选择题(共12小题,满分36分,每小题3分)
1.下列各组图形,可由一个图形平移得到另一个图形的是( )
A. B.
C. D.
2.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
3.如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.经过一点有且只有一条直线与已知直线垂直
4.如图,在△ABC中与∠A构成同旁内角的角有( )
A.5个 B.4个 C.3个 D.2个
5.下列命题中,是假命题的是( )
A.两点之间,线段最短 B.同旁内角互补
C.等角的补角相等 D.垂线段最短
6.下列说法正确的是( )
A.经过已知一点有且只有一条直线与已知直线平行
B.两个相等的角是对顶角
C.互补的两个角一定是邻补角
D.直线外一点与直线上各点连接的所有线段中,垂线段最短
7.如图所示,直线AB,CD相交于点O,OE⊥OF,OF平分∠BOD,∠BOF:∠BOC=1:4,则∠BOE的度数为( )
A.45° B.55° C.60° D.65°
8.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠D=∠DCE D.∠D+∠ACD=180°
9.如图,直线AB,CD被直线CE所截,AB∥CD,∠1=140°,则∠C的度数为( )
A.30° B.40° C.50° D.60°
10.观察下列图形,并阅读图形下面的相关文字,如图所示:两条直线相交,最多有一个交点,三条直线相交,最多有三个交点,四条直线相交,最多有6个交点,像这样,10条直线相交,最多交点的个数是( )
A.40个 B.45个 C.50个 D.55个
11.如图,△ABC平移到△DEF的位置,则下列说法:①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C到点F的方向;④平移距离为线段BD的长.其中说法正确的有( )
A.①② B.①③ C.①④ D.②④
12.如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P,点F为焦点.若∠1=x°,∠2=y°,则∠3 的度数为( )
A.(x﹣y)° B.(180﹣x﹣y)°
C.(180﹣x+y)° D.(x+y﹣90)°
二.填空题(共6小题,满分18分,每小题3分)
13.如图,直线a,b相交于点O.如果∠1+∠2=60°,那么∠3的度数为 .
14.将命题“同角的余角相等”,改写成“如果…,那么…”的形式 .
15.在同一平面内,如果直线a⊥b,直线b⊥c,则a与c的位置关系是 .
16.如图,AB∥CD,BC∥DE,∠B=72°,则∠D= 度.
17.如图所示,某商场重新装修后,准备在门前台阶上铺设地毯,已知这种地毯的批发价为每平方米40元,其台阶的尺寸如图所示,则购买地毯至少需要 元.
18.将一副三角板中的两块直角三角尺按如图方式放置(其中∠ABC=45°,∠D=60°),固定三角尺ABC,将三角尺BDE以每秒30°的速度绕点B按逆时针方向旋转180°停止.在这个过程中,当运动时间为 秒时,三角尺BDE的一边与三角尺ABC的某一边平行(不共线).
三.解答题(共6小题,满分46分)
19.(6分)已知:如图,∠ABD=∠D,BD平分∠ABC.求证:AD∥BC.
20.(7分)如图,直线AB,CD相交于点O,OM⊥AB于点O.
(1)若∠1=∠2,求∠NOD的度数;
(2)若∠BOC=4∠1,求∠AOC,∠MOD的度数.
21.(8分)如图,直线AB∥CD,∠1=70°,∠D=110°,求∠B的度数.
阅读下面的解答过程,并填空(理由或数学式).
解:∵AB∥CD(已知),
∴∠1=(① )(② ).
又∵∠1=70°,∠D=110°(已知),
∴∠1+∠D=180°(等式的性质).
∴∠C+∠D=180°(③ ).
∴(④ )∥(⑤ )(⑥ ).
∴∠B=(⑦ )(⑧ ).
∴∠B=70°
22.(8分)画图并填空:如图,三角形ABC的顶点都在方格纸的格点上,每个格子的边长为1个单位长度,将三角形ABC向上平移3个单位长度,得到三角形A′B′C′.
(1)在图中作出三角形ABC边AB上的高CD;
(2)在图中画出平移后的三角形A′B′C′;
(3)三角形ABC的面积为 ;
(4)若连接AA′,CC′,则这两条线段的关系是 .
23.(8分)如图,∠1=∠C,BE⊥DF于点P.
(1)若∠2=55°,请求出∠B的度数;
(2)若∠2+∠D=90°,求证:AB∥CD.
24.(9分)已知,如图AB∥CD,AF平分∠EAB,DF平分∠EDC.
(1)如图1,探究∠F与∠E的数量关系并证明.
(2)如图2,在(1)的条件下,过A作AH∥ED交DC于点H,AD平分∠EAH,∠DAG:∠FDE=2:7,求∠BAH的度数.
参考答案
一.选择题(共12小题,满分36分,每小题3分)
1.解:A、图形由轴对称所得到,不属于平移,故本选项不符合题意;
B、图形平移前后的形状和大小没有变化,只是位置发生变化,符合平移性质,故本选项符合题意;
C、图形由旋转所得到,不属于平移,故本选项不符合题意;
D、图形大小不一,大小发生变化,不符合平移性质,故本选项不符合题意.
故选:B.
2.解:由对顶角的定义可知,选项B中的∠1与∠2是对顶角,
故选:B.
3.解:如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是垂线段最短.
故选:B.
4.解:在△ABC中与∠A构成同旁内角的角有∠ADE,∠ADF,∠AED,∠C,∠B,共5个.
故选:A.
5.解:A、两点之间,线段最短,是真命题;
B、两直线平行,同旁内角互补,原命题是假命题;
C、等角的补角相等,是真命题;
D、垂线段最短,是真命题;
故选:B.
6.解:A、应为在同一平面内,经过直线外一点有且只有一条直线与已知直线平行,故本选项错误;
B、对顶角相等,但相等的两个角不一定是对顶角,故本选项错误;
C、邻补角互补,但互补的两个角不一定是邻补角,故本选项错误;
D、直线外一点与直线上各点连接的所有线段中,垂线段最短,故本选项正确.
故选:D.
7.解:∵∠BOF:∠BOC=1:4,
∴设∠BOF=x°,则∠BOC=4x°,
∵OF平分∠BOD,
∴∠BOF=∠DOF=x°,
∵∠BOC+∠BOF+∠DOF=180°,
∴4x+x+x=180,
解得:x=30,
∴∠BOF=30°,
∵OE⊥OF,
∴∠EOF=90°,
∴∠BOE=∠EOF﹣∠BOF=60°,
故选:C.
8.解:A.根据内错角相等,两直线平行即可证得AB∥CD;
B.根据内错角相等,两直线平行即可证得BD∥AC,不能证AB∥CD;
C.根据内错角相等,两直线平行即可证得BD∥AC,不能证AB∥CD;
D.根据同旁内角互补,两直线平行,即可证得BD∥AC,不能证AB∥CD.
故选:A.
9.解:∵∠1=140°,
∴∠AEC=180°﹣140°=40°,
∵AB∥CD,
∴∠C=∠AEC=40°.
故选:B.
10.解:2条直线相交,最多有1个交点,即0+1=1(个),
3条直线相交,最多有3个交点,即1+2=3(个),
4条直线相交,最多有6个交点,即1+2+3=6(个),
5条直线相交,最多有10个交点,即1+2+3+4=10(个),
…
10条直线相交,最多有45个交点,即1+2+3+4+5+6+7+8+9=45(个),
故选:B.
11.解:由平移的性质可知,
①AB∥DE,AD=CF=BE,因此正确;
②由平移的性质可知,∠ACB=∠DFE,因此②不正确;
③平移的方向是点C到点F的方向或点A到点D的方向或点B到点E的方向,因此正确;
④平移距离为线段BE或线段AD或线段CF的长,因此④不正确;
综上所述,正确的结论有:①③,
故选:B.
12.解:由题意可知AB∥OF.
∴∠1+∠OFB=180°.
∵∠1=x°.
∴∠OFB=180°﹣x°.
∵∠2=∠POF.
∴∠3=∠POF+∠OFB=(180﹣x+y)°.
故选:C.
二.填空题
13.解:∵∠1+∠2=60°,∠1=∠2(对顶角相等),
∴∠1=∠2=30°,
∵∠1与∠3互为邻补角,
∴∠3=180°﹣∠1=180°﹣30°=150°.
故答案为:150.
14.解:命题“同角的余角相等”,可以改写成:如果两个角是同一个角的余角,那么这两个角相等.
故答案为如果两个角是同一个角的余角,那么这两个角相等.
15.解:如图,
∵a⊥b,
∴∠1=90°,
∵b⊥c,
∴∠2=90°,
∴∠1=∠2,
∴a∥c,
故答案为:a∥c.
16.解:∵AB∥CD,∠B=72°,
∴∠C=∠B=72°,
∵BC∥DE,
∴∠D=180°﹣∠C=180°﹣72°=108°.
故答案为:108.
17.解:利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为1.6米,0.8米,
∴地毯的长度为1.6+0.8=2.4(米),地毯的面积为2.4×2=4.8(平方米),
∴购买地毯至少需要4.8×40=192(元).
故答案为:192.
18.解:当DE∥AB时,如图1,
此时∠ABE=∠E=30°,
∴∠CBE=15°,
t=15°÷30°=0.5;
当BD∥AC时,如图2,
此时∠DBC=45°,
t=45°÷30°=1.5;
当DE∥AC时,如图3,
此时,∠EBC=60°+45°=105°,
t=105°÷30°=3.5;
当BE∥AC时,如图4,
此时∠EBC=90°+45°=135°,
∴t=135°÷30°=4.5;
当DE∥BC时,如图5,
此时∠EBC=90°+60°=150°,
t=150°÷30°=5,
故答案为:0.5或1.5或3.5或4.5或5.
三.解答题
19.证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠ABD=∠D,
∴∠CBD=∠D,
∴AD∥BC.
20.解:(1)∵OM⊥AB,
∴∠AOM=90°,
∴∠AOC+∠1=90°,
∵∠1=∠2,
∴∠AOC+∠2=90°,即∠NOC=90°,
∴∠NOD=180°﹣∠NOC=90°.
∴∠NOD的度数为90°;
(2)∵OM⊥AB,
∴∠BOM=90°,
∵∠BOC=4∠1,
∴∠BOM+∠1=4∠1,即90°+∠1=4∠1,
解得∠1=30°,
∴∠AOC=90°﹣30°=60°,∠MOD=180°﹣∠1=150°.
∴∠AOC的度数为60°,∠MOD的度数为150°.
21.解:∵AB∥CD(已知),
∴∠1=∠C(两直线平行,内错角相等).
又∵∠1=70°,∠D=110°(已知),
∴∠1+∠D=180°(等式的性质).
∴∠C+∠D=180° (等量代换),
∴AC∥BD(同旁内角互补,两直线平行),
∴∠B=∠1(两直线平行,同位角相等),
∴∠B=70°,
故答案为:∠C;两直线平行,内错角相等;等量代换;AC;BD;同旁内角互补,两直线平行;∠1;两直线平行,同位角相等.
22.解:(1)如图,线段CD即为所求;
(2)如图,△A′B′C′即为所求;
(3)S△ABC=AB CD=×4×4=8,
故答案为:8;
(4)AA′=CC′,AA′∥CC′,
故答案为:AA′=CC′,AA′∥CC′.
23.(1)解:∵∠1=∠C(已知),
∴BE∥CF(同位角相等,两直线平行),
∴∠B=∠2=55°(两直线平行,同位角相等);
(2)证明:∵BE⊥DF(已知),
∴∠DPE=90°(垂直定义),
∵BE∥CF(已证),
∴∠CFD=∠DPE=90°(两直线平行,同位角相等),
∴∠2+∠BFD=180﹣∠CFD=90°(平角定义),
∵∠2+∠D=90°(已知),
∴∠BFD=∠D(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
24.(1)2∠AFD+∠AED=360°,
证明:如图,过点E作EM∥AB,过点F作FN∥AB,
∵FN∥AB,
∴∠NFA=∠BAF,
∵AF平分∠EAB,
∴∠EAB=2∠BAF,
∴∠EAB=2∠NAF,
∵FN∥AB,AB∥CD,
∴FN∥CD,
∴∠NFD=∠FDC,
∵DF平分∠EDC,
∴∠EDC=2∠FDC,
∴∠EDC=2∠NFD,
∴∠BAE+∠EDC=2(∠NFA+∠NFD)=2∠AFD,
∵AB∥CD,
∴EM∥CD,
∵EM∥AB,
∴∠BAE+∠AEM=180°,
∵EM∥CD,
∴∠DEM+∠EDC=180°,
∴(∠BAE+∠AEM)+(∠DEM+∠EDC)=360°,
即∠BAE+∠AED+∠EDC=360°,
∴∠AED=360°﹣(∠EAB+∠EDC)=360°﹣2∠AFD,
2∠AFD+∠AED=360°;
(2)解:∵∠DAG:∠FDE=2:7,
∴设∠DAG=2α,∠FDE=∠FDG=7α,
∴∠EDH=2∠FDG=14α,
∵∠GAD=∠GAE﹣∠DAE=∠BAE﹣∠EAH=∠BAH,
∴∠BAH=4α,
∵AB∥CD,
∴∠AHD=∠BAH=4α,
∵AH∥ED,
∴∠AHD+∠EDH=180°,
∴4α+14α=180°,
解得:α=10°,
∴∠BAH=4α=40°.
