17.1 勾股定理 培优练习(无答案)人教版八年级数学下册
文档属性
| 名称 | 17.1 勾股定理 培优练习(无答案)人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 219.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 00:00:00 | ||
图片预览

文档简介
17.1 勾股定理
一、选择题。
1.在Rt△ABC中,∠B=90°,AB=5,BC=4,则AC的长是( )
A.3 B.4 C.3或 D.
2.正方形的对角线长为,则其周长为( )
A.8 B. C. D.16
3.在△ABC中,AB=AC,AD是BC边上的高,若AB=5cm,BC=6cm,则AD的长是( )
A.3cm B.4cm C.5cm D.6cm
4.如图,阴影部分是两个正方形,其他三个是一个正方形和两个直角三角形( )
A.8 B.25 C.49 D.64
5.赵爽弦图由四个全等的直角三角形所组成,形成一个大正方形,中间是一个小正方形(如图所示),小浔绘制了一幅赵爽弦图,她将EG延长交CD于点I.记小正方形EFGH的面积为S1,大正方形ABCD的面积为S2,若DI=2,CI=1,S2=5S1,则GI的值是( )
A. B. C. D.
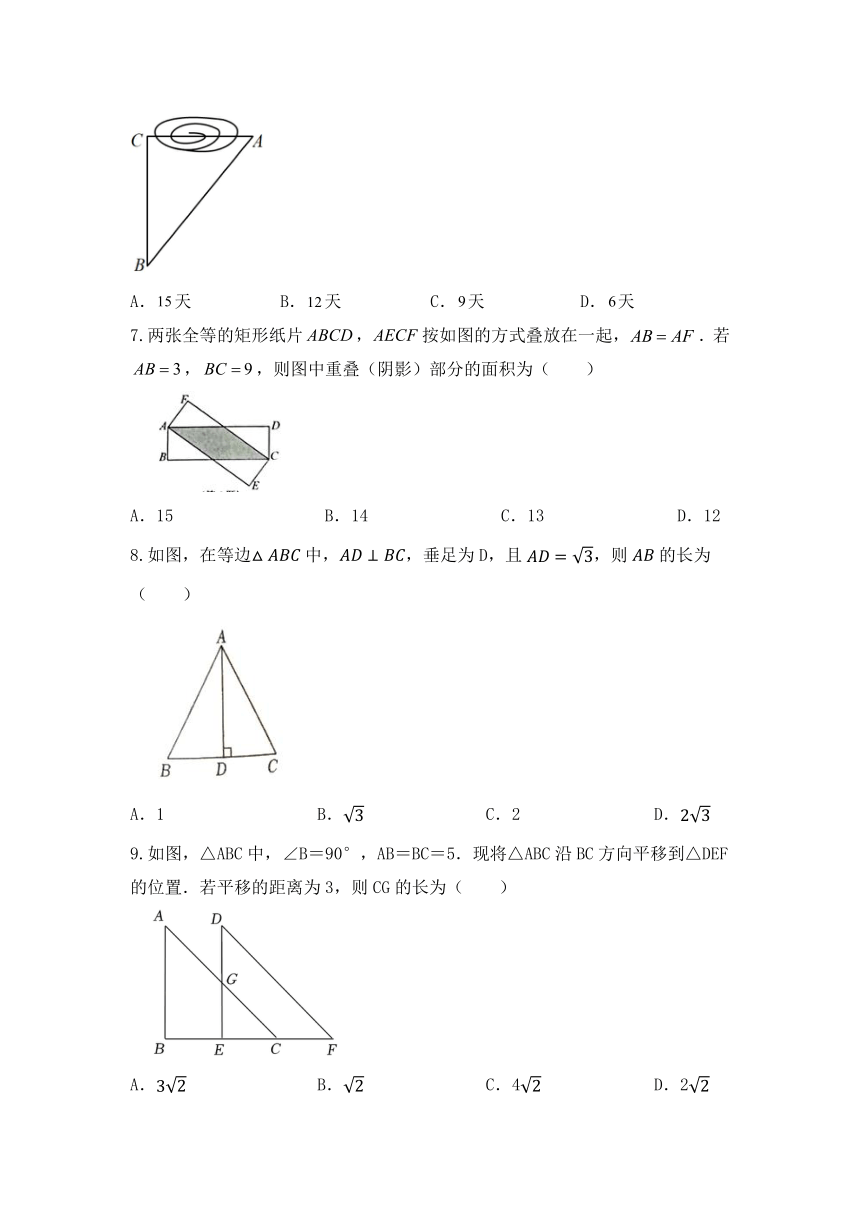
6.如图,为修铁路需凿通隧道,测得,,,若每天凿,则把隧道凿通需要( )
A.天 B.天 C.天 D.天
7.两张全等的矩形纸片,按如图的方式叠放在一起,.若,,则图中重叠(阴影)部分的面积为( )
A.15 B.14 C.13 D.12
8.如图,在等边中,,垂足为D,且,则的长为( )
A.1 B. C.2 D.
9.如图,△ABC中,∠B=90°,AB=BC=5.现将△ABC沿BC方向平移到△DEF的位置.若平移的距离为3,则CG的长为( )
A. B. C.4 D.2
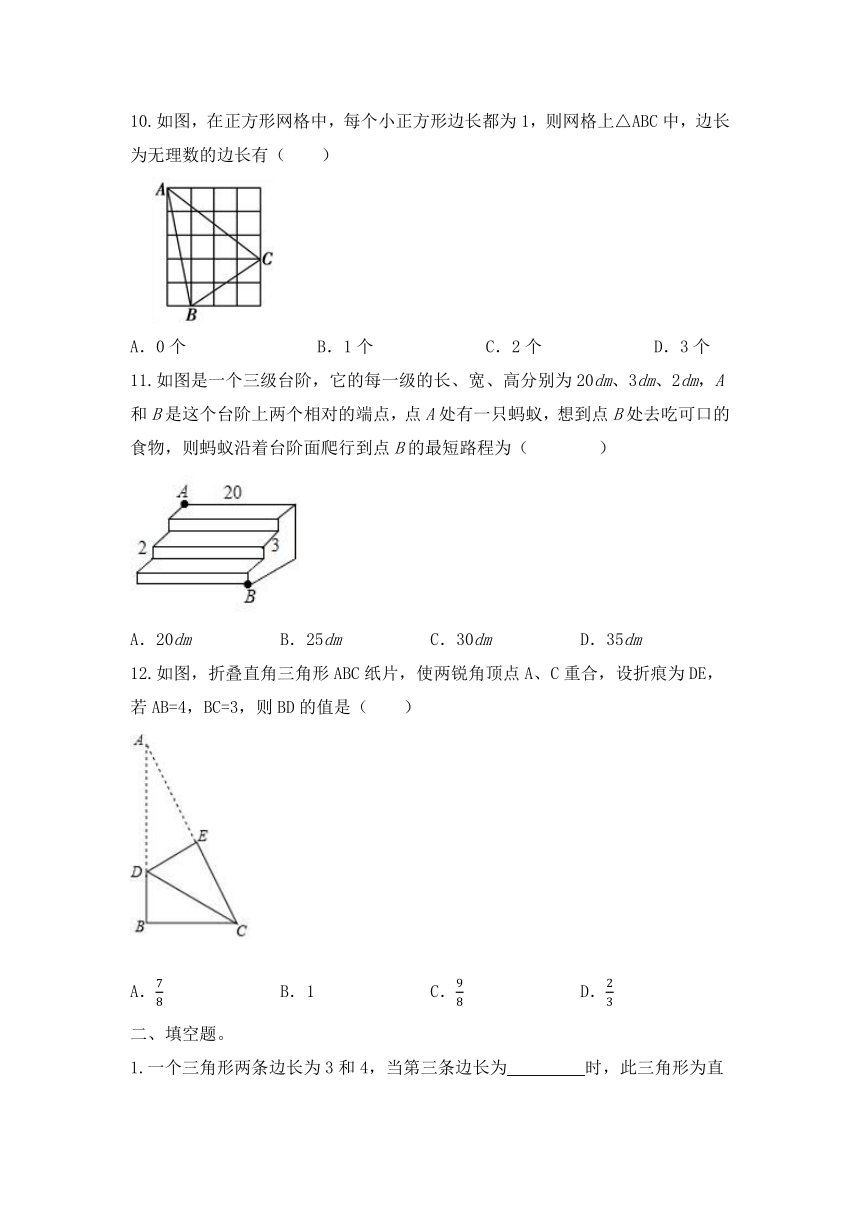
10.如图,在正方形网格中,每个小正方形边长都为1,则网格上△ABC中,边长为无理数的边长有( )
A.0个 B.1个 C.2个 D.3个
11.如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )
A.20dm B.25dm C.30dm D.35dm
12.如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE,若AB=4,BC=3,则BD的值是( )
A. B.1 C. D.
二、填空题。
1.一个三角形两条边长为3和4,当第三条边长为 时,此三角形为直角三角形.
2.已知,在中,,,,则的面积为 __.
3.如图, 在平面直角坐标系中点A的坐标为,点B为x轴上的动点,若为等腰三角形,则B点的位置有 种.
4.如图.中,,,,,则 , .
5.如图,△ABC中,AB=AC,DE平分∠ADC,EF⊥AB交AD于G,BC=6,则BF= .
6.如图,一根长16cm的牙刷置于底面直径为6cm、高8cm的圆柱形水杯中,牙刷露在杯子外面的长度为hcm,则h的取值范围是 .
三、解答题。
1.如图,一高层住宅发生火灾,消防车立即赶到距大厦12米(的长)处,升起云梯到火灾窗口,云梯长20米,云梯底部距地面3米(的长),问:发生火灾的住户窗口距离地面有多高(的长)?
2.如图和都是等腰直角三角形,,,顶点在的斜边上,求证:.
3.如图,在中,,,.求的长以及的面积.
4.如图,点O是位于东西海岸线的一个港口,A,B两艘客轮从港口O同时出发,A客轮沿北偏东75°航行,航速是每小时18海里,B客轮沿北偏西15°方向航行,航速是每小时24海里,请计算3小时之后两客轮之间的距离.
5.如图,.
(1)尺规作图:作的垂直平分线交于点D,交于点E(不写作法,保留作图痕迹);
(2)在(1)的基础上,连接,求的长.
6.如图,在Rt△ABC中,∠C=90°,AC=6cm,动点P从点B出发,设运动时间为t秒.
(1)求BC的长;
(2)在点P的运动过程中,是否存在某个时刻t,使得点P到边AB的距离与点P到点C的距离相等?若存在;若不存在,请说明理由.
一、选择题。
1.在Rt△ABC中,∠B=90°,AB=5,BC=4,则AC的长是( )
A.3 B.4 C.3或 D.
2.正方形的对角线长为,则其周长为( )
A.8 B. C. D.16
3.在△ABC中,AB=AC,AD是BC边上的高,若AB=5cm,BC=6cm,则AD的长是( )
A.3cm B.4cm C.5cm D.6cm
4.如图,阴影部分是两个正方形,其他三个是一个正方形和两个直角三角形( )
A.8 B.25 C.49 D.64
5.赵爽弦图由四个全等的直角三角形所组成,形成一个大正方形,中间是一个小正方形(如图所示),小浔绘制了一幅赵爽弦图,她将EG延长交CD于点I.记小正方形EFGH的面积为S1,大正方形ABCD的面积为S2,若DI=2,CI=1,S2=5S1,则GI的值是( )
A. B. C. D.
6.如图,为修铁路需凿通隧道,测得,,,若每天凿,则把隧道凿通需要( )
A.天 B.天 C.天 D.天
7.两张全等的矩形纸片,按如图的方式叠放在一起,.若,,则图中重叠(阴影)部分的面积为( )
A.15 B.14 C.13 D.12
8.如图,在等边中,,垂足为D,且,则的长为( )
A.1 B. C.2 D.
9.如图,△ABC中,∠B=90°,AB=BC=5.现将△ABC沿BC方向平移到△DEF的位置.若平移的距离为3,则CG的长为( )
A. B. C.4 D.2
10.如图,在正方形网格中,每个小正方形边长都为1,则网格上△ABC中,边长为无理数的边长有( )
A.0个 B.1个 C.2个 D.3个
11.如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )
A.20dm B.25dm C.30dm D.35dm
12.如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE,若AB=4,BC=3,则BD的值是( )
A. B.1 C. D.
二、填空题。
1.一个三角形两条边长为3和4,当第三条边长为 时,此三角形为直角三角形.
2.已知,在中,,,,则的面积为 __.
3.如图, 在平面直角坐标系中点A的坐标为,点B为x轴上的动点,若为等腰三角形,则B点的位置有 种.
4.如图.中,,,,,则 , .
5.如图,△ABC中,AB=AC,DE平分∠ADC,EF⊥AB交AD于G,BC=6,则BF= .
6.如图,一根长16cm的牙刷置于底面直径为6cm、高8cm的圆柱形水杯中,牙刷露在杯子外面的长度为hcm,则h的取值范围是 .
三、解答题。
1.如图,一高层住宅发生火灾,消防车立即赶到距大厦12米(的长)处,升起云梯到火灾窗口,云梯长20米,云梯底部距地面3米(的长),问:发生火灾的住户窗口距离地面有多高(的长)?
2.如图和都是等腰直角三角形,,,顶点在的斜边上,求证:.
3.如图,在中,,,.求的长以及的面积.
4.如图,点O是位于东西海岸线的一个港口,A,B两艘客轮从港口O同时出发,A客轮沿北偏东75°航行,航速是每小时18海里,B客轮沿北偏西15°方向航行,航速是每小时24海里,请计算3小时之后两客轮之间的距离.
5.如图,.
(1)尺规作图:作的垂直平分线交于点D,交于点E(不写作法,保留作图痕迹);
(2)在(1)的基础上,连接,求的长.
6.如图,在Rt△ABC中,∠C=90°,AC=6cm,动点P从点B出发,设运动时间为t秒.
(1)求BC的长;
(2)在点P的运动过程中,是否存在某个时刻t,使得点P到边AB的距离与点P到点C的距离相等?若存在;若不存在,请说明理由.
