第四章 专题 杆、线和弹簧受力分析 导学案 高一上学期物理人教版(2019)必修第一册
文档属性
| 名称 | 第四章 专题 杆、线和弹簧受力分析 导学案 高一上学期物理人教版(2019)必修第一册 | 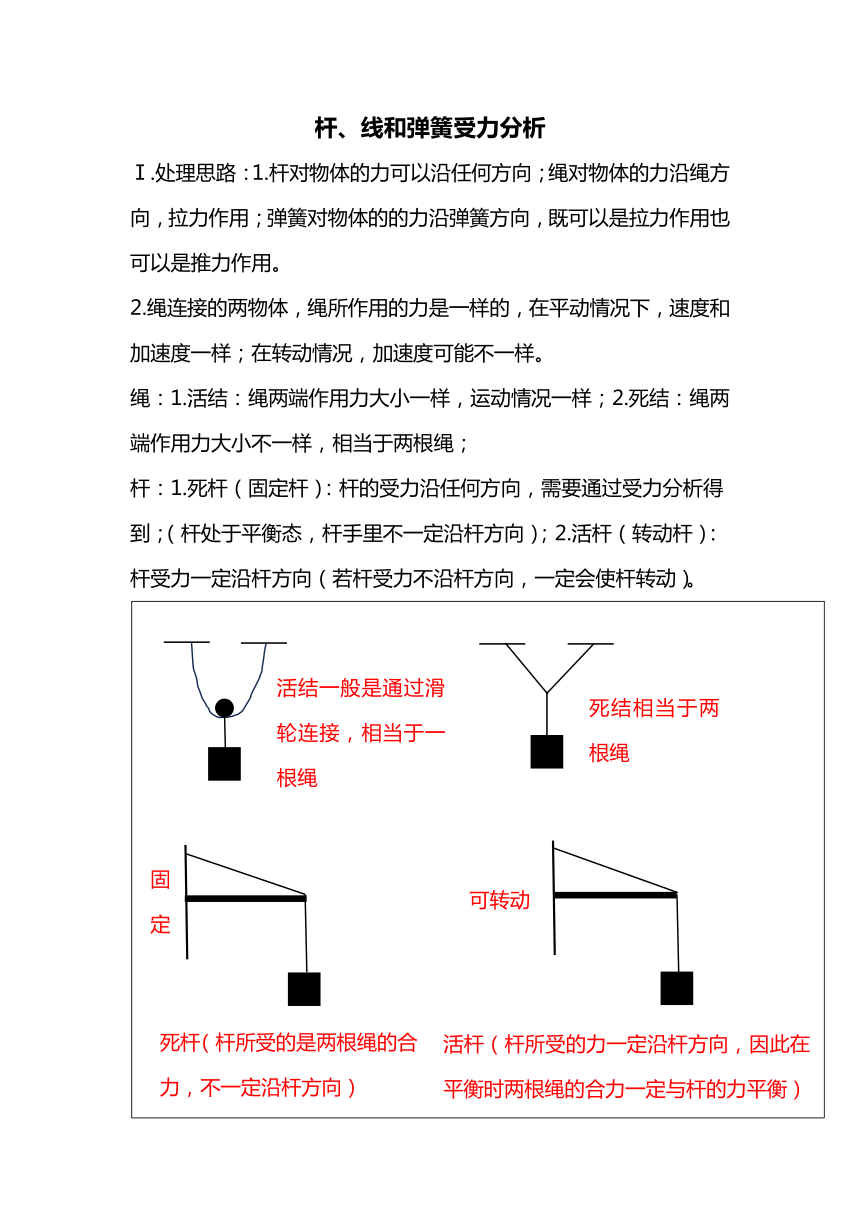 | |
| 格式 | docx | ||
| 文件大小 | 175.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-16 13:24:22 | ||
图片预览


文档简介
杆、线和弹簧受力分析
Ⅰ.处理思路:1.杆对物体的力可以沿任何方向;绳对物体的力沿绳方向,拉力作用;弹簧对物体的的力沿弹簧方向,既可以是拉力作用也可以是推力作用。
2.绳连接的两物体,绳所作用的力是一样的,在平动情况下,速度和加速度一样;在转动情况,加速度可能不一样。
绳:1.活结:绳两端作用力大小一样,运动情况一样;2.死结:绳两端作用力大小不一样,相当于两根绳;
杆:1.死杆(固定杆):杆的受力沿任何方向,需要通过受力分析得到;(杆处于平衡态,杆手里不一定沿杆方向);2.活杆(转动杆):杆受力一定沿杆方向(若杆受力不沿杆方向,一定会使杆转动)。
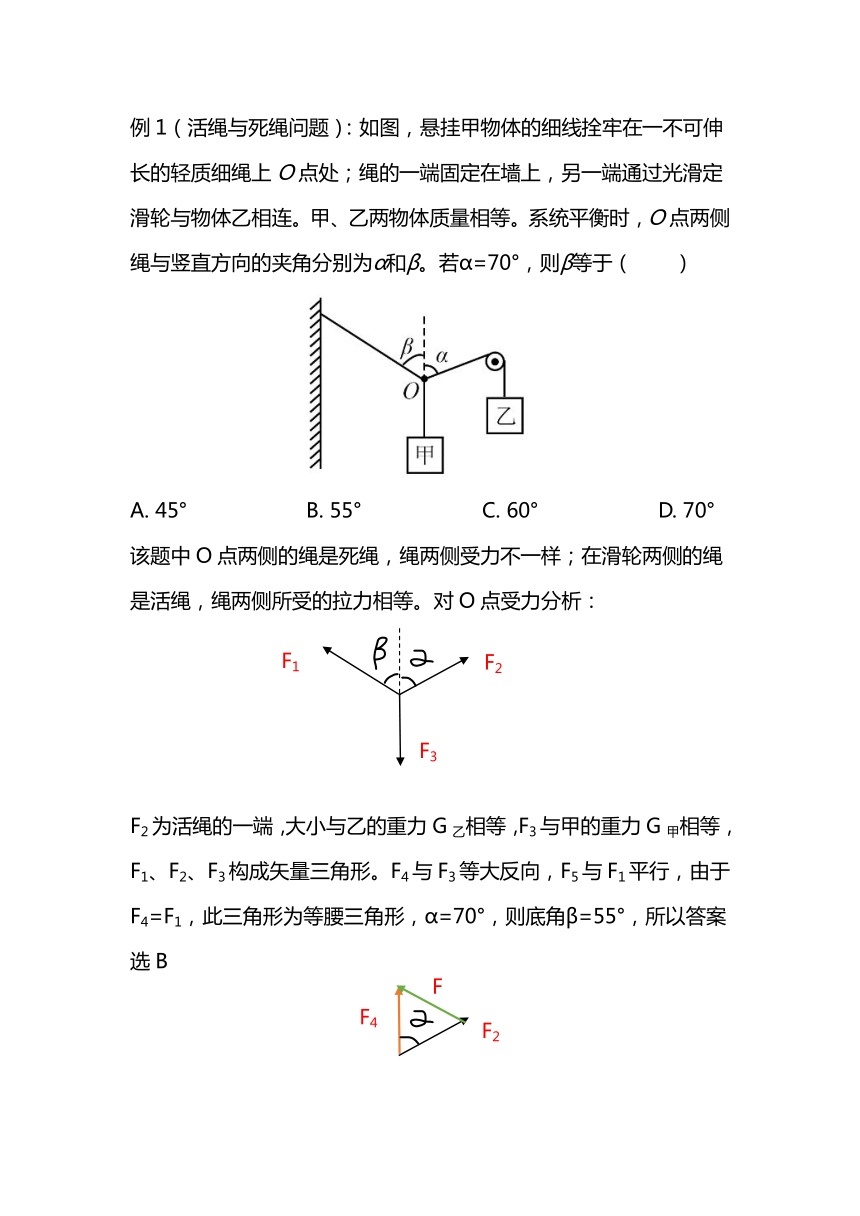
例1(活绳与死绳问题):如图,悬挂甲物体的细线拴牢在一不可伸长的轻质细绳上O点处;绳的一端固定在墙上,另一端通过光滑定滑轮与物体乙相连。甲、乙两物体质量相等。系统平衡时,O点两侧绳与竖直方向的夹角分别为α和β。若α=70°,则β等于( )
A. 45° B. 55° C. 60° D. 70°
该题中O点两侧的绳是死绳,绳两侧受力不一样;在滑轮两侧的绳是活绳,绳两侧所受的拉力相等。对O点受力分析:
F2为活绳的一端,大小与乙的重力G乙相等,F3与甲的重力G甲相等,F1、F2、F3构成矢量三角形。F4与F3等大反向,F5与F1平行,由于F4=F1,此三角形为等腰三角形,α=70°,则底角β=55°,所以答案选B
例2(弹簧受力问题):如图所示,质量分别为m1、m2的两个物体通过轻弹簧连接,在力F的作用下一起沿水平方向做匀速直线运动(m1在地面,m2在空中),力F与水平方向成θ角。则m1所受支持力和摩檫力f正确的是()
A.N=m1g+m2g-Fsinθ B. N=m1g+m2g-Fcosθ
C.f=Fcosθ D.f=Fsinθ
弹簧对m1是推力作用,对m2是拉力作用。把m1 和m2看成整体,受力分析:
G总=(m1+ m2)g 正交分解法:
竖直方向:G总=N+Fsinθ 水平方向:Fcosθ=f 因此答案为AC
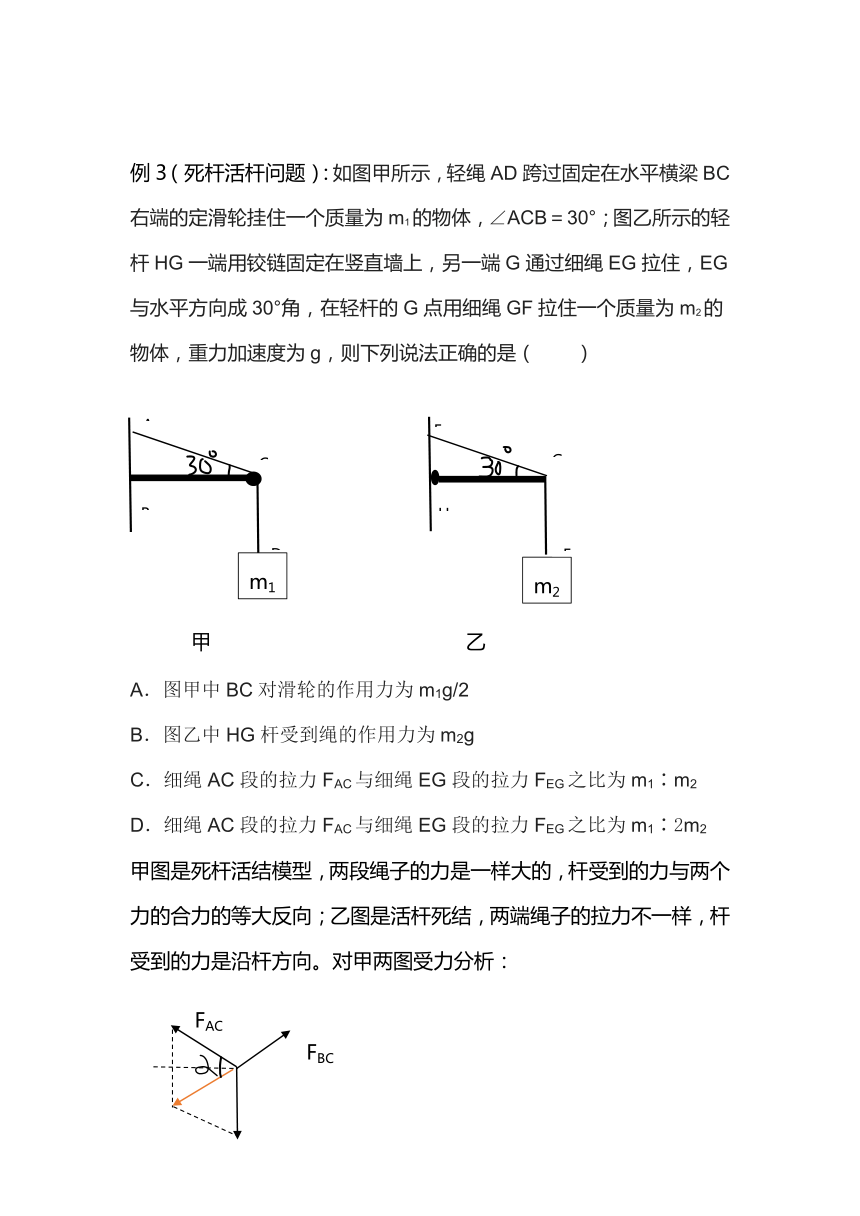
例3(死杆活杆问题):如图甲所示,轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为m1的物体,∠ACB=30°;图乙所示的轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向成30°角,在轻杆的G点用细绳GF拉住一个质量为m2的物体,重力加速度为g,则下列说法正确的是( )
A.图甲中BC对滑轮的作用力为m1g/2
B.图乙中HG杆受到绳的作用力为m2g
C.细绳AC段的拉力FAC与细绳EG段的拉力FEG之比为m1∶m2
D.细绳AC段的拉力FAC与细绳EG段的拉力FEG之比为m1∶2m2
甲图是死杆活结模型,两段绳子的力是一样大的,杆受到的力与两个力的合力的等大反向;乙图是活杆死结,两端绳子的拉力不一样,杆受到的力是沿杆方向。对甲两图受力分析:
甲图死杆活结,FAB=FCD=m1g,F合为FAB和FCD的合力,FBC与F合等大反向。图中α=60°,所以FBC=m1g=FAC=FCD
对乙图受力分析:
乙图活杆死结,杆的力为FHG沿杆方向,FGF =m2g,F合为FEG和FGF的合力,FHG与F合等大反向。图中γ=30°,所以FEG= 2FGF=2 m2g,
FHG= m2g。FAC:FEG=m1:2m2,选D。
课后练习:
1.如图所示,一轻质横杆O端用铰链固定于墙上,A端用轻绳拉紧使OA杆保持水平。若在A端挂一重物G,在把重物的悬点从A向O缓慢移动的过程中,下列判断中正确的是()
A.墙对杆的作用力一直变大
B.墙对杆的作用力先变小后变大
C.墙对杆的作用力先变大后变小
D.墙对杆的作用力的最小值为Gcosθ
2. 如图所示,轻质不可伸长的晾衣绳两端分别固定在竖直杆M、N上的a、b两点,悬挂衣服的衣架钩是光滑的,挂于绳上处于静止状态。如果只人为改变一个条件,当衣架静止时,下列说法正确的是( )
A.绳的右端上移到,绳子拉力不变
B.将杆N向右移一些,绳子拉力变大
C.绳的两端高度差越小,绳子拉力越小
D.若换挂质量更大的衣服,则衣架悬挂点右移
Ⅱ.处理思路:1.弹簧在受力瞬间,力不会发生突变,因为弹簧形变需要时间;杆、绳在受力时,力会发生突变,因为杆和绳的形变量较小,形变不需要时间,可以认为是瞬间产生的。
2.轻质物体质量不计(m=0),根据牛顿第二定律F=ma,F为0时,轻质物体始终处于平衡态。
例1(轻质物体):如图所示,一弹簧秤放在光滑水平面上,外壳质量为m。弹簧及挂钩质量不计,施以水平F1、F2使其沿F1方向产生加速度a,则弹簧秤的示数()
A.F1 B.F2 C. D.ma
解析:挂钩与弹簧相连,轻挂钩和轻弹簧质量不计,由F合=ma,m=0,F合=0,F1=F弹,故弹簧两端的受力都是F1,选B。
例2(绳弹簧瞬间突变问题):如图所示,A、B、C三球质量均为m,用轻绳及轻弹簧悬挂处于平衡状态。现剪断悬挂在天花板的轻绳。求剪短轻绳瞬间小球C的加速度及连接A、B球绳的张力。
解析:剪断轻绳瞬间,A、B之间的轻绳会瞬间发生形变,B、C之间的弹簧不会发生形变。对A、B整体受力分析,A、B受到弹簧的弹力和两球的重力:
F弹=mg,对于A、B合力是F合=mg+mg+mg=3mg,aA=aB=,对B单独受力分析:
mg+ F弹- FT=m aB得FT=0.5mg。
由于F弹在剪断瞬间力的大小不变,与重力相等,aC=0
课后练习:
1.如图所示,质量分别为m、2m的小球A、B,由轻质弹簧相连后再用细线悬挂在正在竖直向上做匀减速运动的电梯内,细线承受的拉力为F,此时突然剪断细线,在绳断瞬间,弹簧的弹力大小为
小球A的加速度大小为
2.某青年的质量是某少年质量的2倍,该青年能施加的最大拉力是该少年能施加的最大拉力的2倍。设想该青年和少年在太空中拔河,他们最初静止与空中,然后分别抓紧轻绳子的两端尽力对拉。那么,对拉时青年和少年的加速度大小之比为多少?
Ⅰ.处理思路:1.杆对物体的力可以沿任何方向;绳对物体的力沿绳方向,拉力作用;弹簧对物体的的力沿弹簧方向,既可以是拉力作用也可以是推力作用。
2.绳连接的两物体,绳所作用的力是一样的,在平动情况下,速度和加速度一样;在转动情况,加速度可能不一样。
绳:1.活结:绳两端作用力大小一样,运动情况一样;2.死结:绳两端作用力大小不一样,相当于两根绳;
杆:1.死杆(固定杆):杆的受力沿任何方向,需要通过受力分析得到;(杆处于平衡态,杆手里不一定沿杆方向);2.活杆(转动杆):杆受力一定沿杆方向(若杆受力不沿杆方向,一定会使杆转动)。
例1(活绳与死绳问题):如图,悬挂甲物体的细线拴牢在一不可伸长的轻质细绳上O点处;绳的一端固定在墙上,另一端通过光滑定滑轮与物体乙相连。甲、乙两物体质量相等。系统平衡时,O点两侧绳与竖直方向的夹角分别为α和β。若α=70°,则β等于( )
A. 45° B. 55° C. 60° D. 70°
该题中O点两侧的绳是死绳,绳两侧受力不一样;在滑轮两侧的绳是活绳,绳两侧所受的拉力相等。对O点受力分析:
F2为活绳的一端,大小与乙的重力G乙相等,F3与甲的重力G甲相等,F1、F2、F3构成矢量三角形。F4与F3等大反向,F5与F1平行,由于F4=F1,此三角形为等腰三角形,α=70°,则底角β=55°,所以答案选B
例2(弹簧受力问题):如图所示,质量分别为m1、m2的两个物体通过轻弹簧连接,在力F的作用下一起沿水平方向做匀速直线运动(m1在地面,m2在空中),力F与水平方向成θ角。则m1所受支持力和摩檫力f正确的是()
A.N=m1g+m2g-Fsinθ B. N=m1g+m2g-Fcosθ
C.f=Fcosθ D.f=Fsinθ
弹簧对m1是推力作用,对m2是拉力作用。把m1 和m2看成整体,受力分析:
G总=(m1+ m2)g 正交分解法:
竖直方向:G总=N+Fsinθ 水平方向:Fcosθ=f 因此答案为AC
例3(死杆活杆问题):如图甲所示,轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为m1的物体,∠ACB=30°;图乙所示的轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向成30°角,在轻杆的G点用细绳GF拉住一个质量为m2的物体,重力加速度为g,则下列说法正确的是( )
A.图甲中BC对滑轮的作用力为m1g/2
B.图乙中HG杆受到绳的作用力为m2g
C.细绳AC段的拉力FAC与细绳EG段的拉力FEG之比为m1∶m2
D.细绳AC段的拉力FAC与细绳EG段的拉力FEG之比为m1∶2m2
甲图是死杆活结模型,两段绳子的力是一样大的,杆受到的力与两个力的合力的等大反向;乙图是活杆死结,两端绳子的拉力不一样,杆受到的力是沿杆方向。对甲两图受力分析:
甲图死杆活结,FAB=FCD=m1g,F合为FAB和FCD的合力,FBC与F合等大反向。图中α=60°,所以FBC=m1g=FAC=FCD
对乙图受力分析:
乙图活杆死结,杆的力为FHG沿杆方向,FGF =m2g,F合为FEG和FGF的合力,FHG与F合等大反向。图中γ=30°,所以FEG= 2FGF=2 m2g,
FHG= m2g。FAC:FEG=m1:2m2,选D。
课后练习:
1.如图所示,一轻质横杆O端用铰链固定于墙上,A端用轻绳拉紧使OA杆保持水平。若在A端挂一重物G,在把重物的悬点从A向O缓慢移动的过程中,下列判断中正确的是()
A.墙对杆的作用力一直变大
B.墙对杆的作用力先变小后变大
C.墙对杆的作用力先变大后变小
D.墙对杆的作用力的最小值为Gcosθ
2. 如图所示,轻质不可伸长的晾衣绳两端分别固定在竖直杆M、N上的a、b两点,悬挂衣服的衣架钩是光滑的,挂于绳上处于静止状态。如果只人为改变一个条件,当衣架静止时,下列说法正确的是( )
A.绳的右端上移到,绳子拉力不变
B.将杆N向右移一些,绳子拉力变大
C.绳的两端高度差越小,绳子拉力越小
D.若换挂质量更大的衣服,则衣架悬挂点右移
Ⅱ.处理思路:1.弹簧在受力瞬间,力不会发生突变,因为弹簧形变需要时间;杆、绳在受力时,力会发生突变,因为杆和绳的形变量较小,形变不需要时间,可以认为是瞬间产生的。
2.轻质物体质量不计(m=0),根据牛顿第二定律F=ma,F为0时,轻质物体始终处于平衡态。
例1(轻质物体):如图所示,一弹簧秤放在光滑水平面上,外壳质量为m。弹簧及挂钩质量不计,施以水平F1、F2使其沿F1方向产生加速度a,则弹簧秤的示数()
A.F1 B.F2 C. D.ma
解析:挂钩与弹簧相连,轻挂钩和轻弹簧质量不计,由F合=ma,m=0,F合=0,F1=F弹,故弹簧两端的受力都是F1,选B。
例2(绳弹簧瞬间突变问题):如图所示,A、B、C三球质量均为m,用轻绳及轻弹簧悬挂处于平衡状态。现剪断悬挂在天花板的轻绳。求剪短轻绳瞬间小球C的加速度及连接A、B球绳的张力。
解析:剪断轻绳瞬间,A、B之间的轻绳会瞬间发生形变,B、C之间的弹簧不会发生形变。对A、B整体受力分析,A、B受到弹簧的弹力和两球的重力:
F弹=mg,对于A、B合力是F合=mg+mg+mg=3mg,aA=aB=,对B单独受力分析:
mg+ F弹- FT=m aB得FT=0.5mg。
由于F弹在剪断瞬间力的大小不变,与重力相等,aC=0
课后练习:
1.如图所示,质量分别为m、2m的小球A、B,由轻质弹簧相连后再用细线悬挂在正在竖直向上做匀减速运动的电梯内,细线承受的拉力为F,此时突然剪断细线,在绳断瞬间,弹簧的弹力大小为
小球A的加速度大小为
2.某青年的质量是某少年质量的2倍,该青年能施加的最大拉力是该少年能施加的最大拉力的2倍。设想该青年和少年在太空中拔河,他们最初静止与空中,然后分别抓紧轻绳子的两端尽力对拉。那么,对拉时青年和少年的加速度大小之比为多少?
