平面与平面平行的判定(浙江省台州市)
文档属性
| 名称 | 平面与平面平行的判定(浙江省台州市) |  | |
| 格式 | rar | ||
| 文件大小 | 192.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-06 14:45:00 | ||
图片预览


文档简介
课件17张PPT。2.2.2平面与平面平行的判定1.直线与平面平行的判定定理是什么?复习引入:2. 空间中两个平面具有怎样的位置关系呢?相交或平行
体现的数学思想是什么?
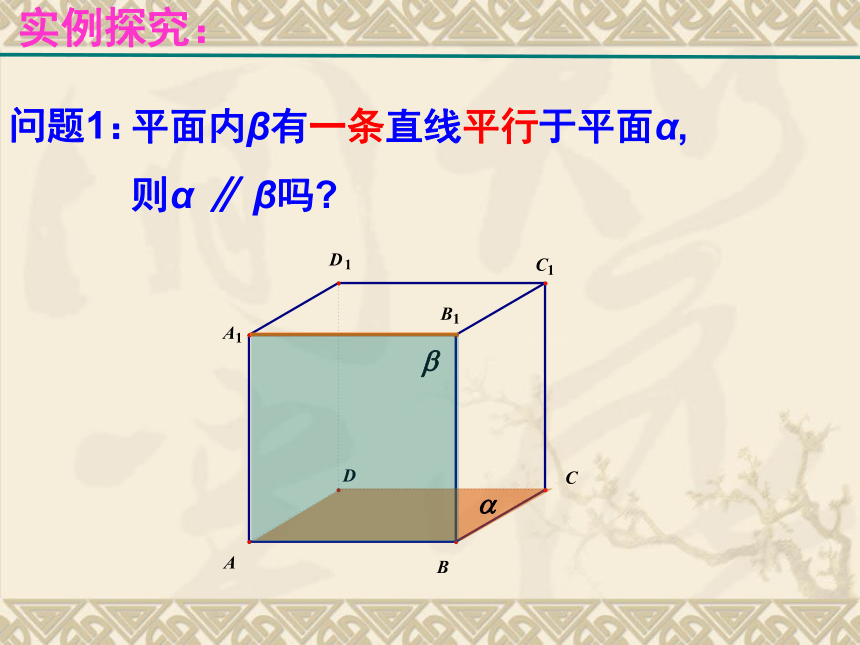
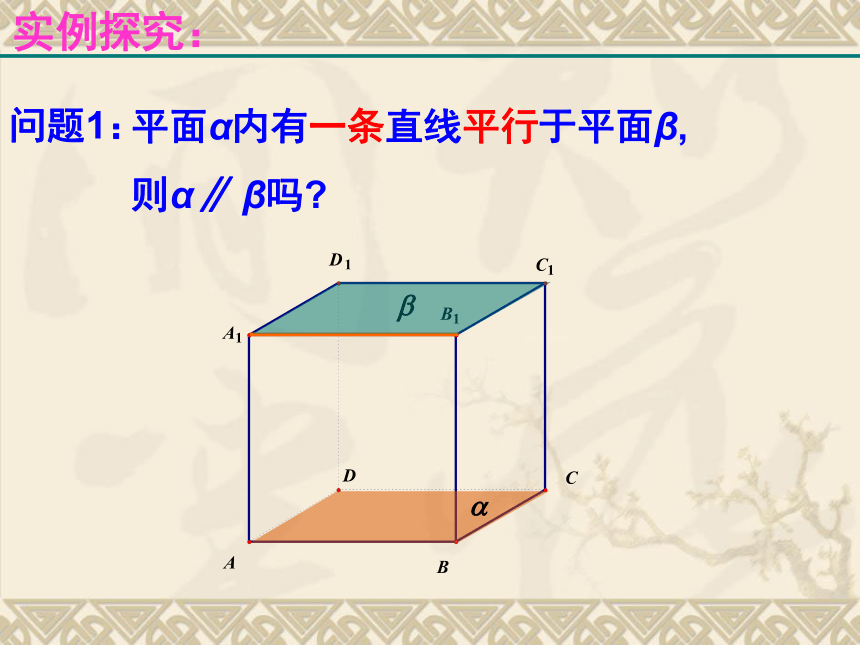
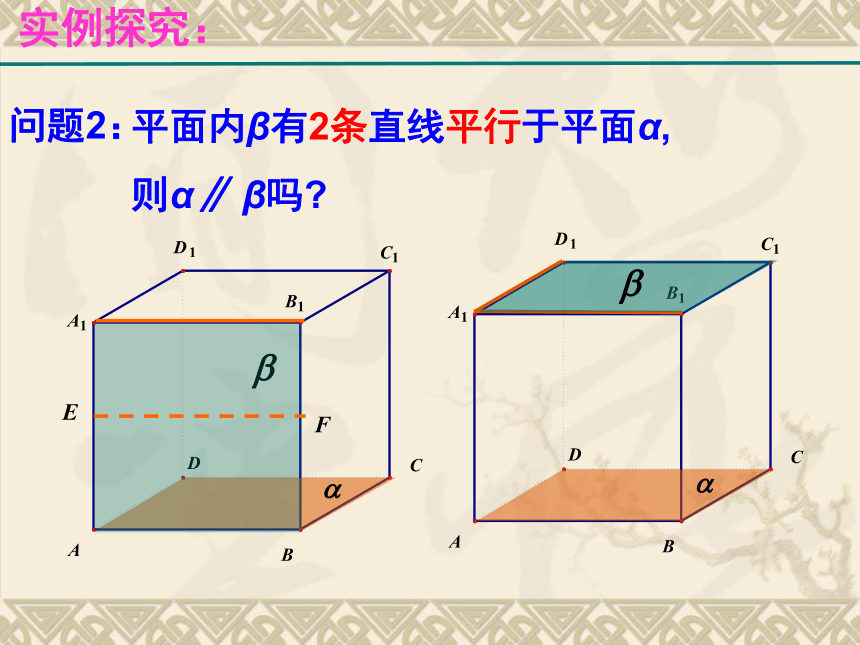
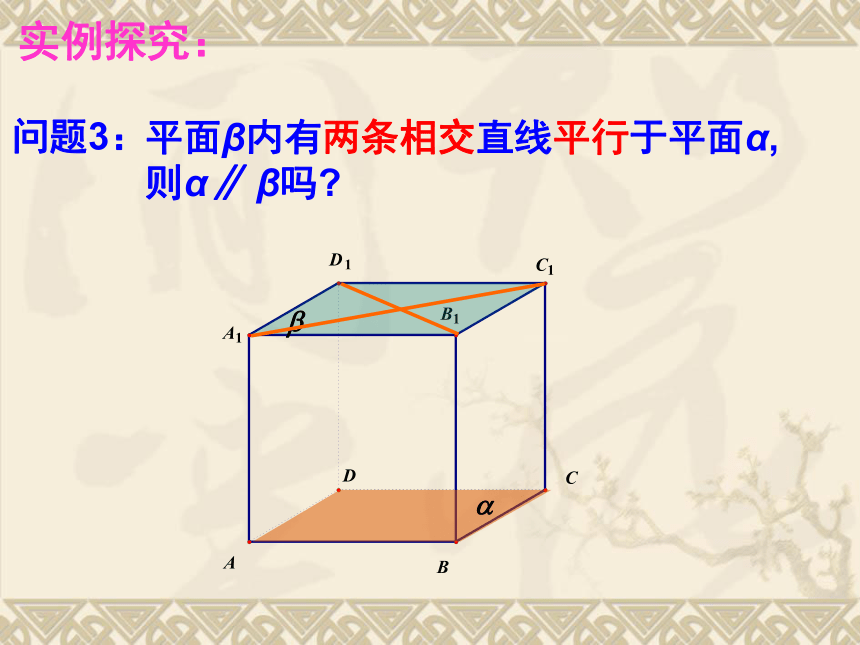
观察并实践:(1)三角板或者课本的一边所在直线与桌面平行,这个三角板或者课本所在平面与桌面平行吗?(2)三角板的两条边所在直线分别与桌面平行,三角板所在平面与桌面平行吗?(3)课本的两条边所在直线分别与桌面平行,课本所在平面与桌面平行吗?从实践(1)(2)(3)中你可以得到什么结论?实例探究:实例探究:实例探究:实例探究: 定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.平面与平面平行判定定理抽象概括: (1)定义法:证明平面与平面无公共点; (2)判定定理: 怎样判定平面与平面平行?方法提炼:例1:平面?与平面?平行的条件可以是( )A. ?内有无穷多条直线都与?平行.B. 直线a//? , a // ?,且直线a不在?内,也不在?内.C. 直线a ì ? ,b ì ?,且a // ? ,b// ?D. ?内的任何直线与?平行.典型例题:D例2: 已知正方体ABCD-A1B1C1D1,求证:平面AB1D1//平面C1BD.典型例题 变式:已知正方体ABCD-A1B1C1D1,M、N、E、F分别是棱A1B1,A1D1,B1C1 ,C1D1的中点。求证:平面AMN//平面EFDB.例2、已知正方体ABCD-A1B1C1D1,
求证:平面AB1D1∥平面C1BD.分析:四边形ABC1D1为平行四边形.,即AD1∥BC1
同理四边形DBB1D1为平行四边形.即D1B1∥DB
变式:已知正方体ABCD-A1B1C1D1,M、N、E、F分别是棱A1B1,A1D1,B1C1 ,C1D1的中点。求证:平面AMN//平面EFDB.证明:∵M、N、 F 、 E分别为棱B1A1、A1D1、D1C1、C1B1的中点.NM 平面DBEF∴NEBA为平行四边形,∴AN∥BE,又∵AN∩NM=N∴平面AMN//平面EFDB又∵BE 平面DBEF如图,在正方体ABCD—A1B1C1D1中,E、F、G分别是棱BC、C1D1、 B1C1的中点。
求证(1)平面EFG//平面BDD1B1.
(2)EF//平面BDD1B1.试一试:2.应用判定定理判定面面平行时应注意:
两条相交直线小结:1.平面与平面平行的判定:3.应用判定定理判定面面平行的关键是找平行线方法一:三角形的中位线定理;方法二:平行四边形的平行关系。 线线平行 1 、想一想2、判断 面面平行 线面平行? 如果一个平面内有两条相交直线
分别平行于另一个平面内的两条相交
直线,那么这两个平面平行课外延伸:2、归纳平面与平面平行的判定定理推论 ?作业:A:小结
B:P62 A7
P52 B1(1)做模型,画直观图
(2)写过程,分“找”和“求”两步
体现的数学思想是什么?
观察并实践:(1)三角板或者课本的一边所在直线与桌面平行,这个三角板或者课本所在平面与桌面平行吗?(2)三角板的两条边所在直线分别与桌面平行,三角板所在平面与桌面平行吗?(3)课本的两条边所在直线分别与桌面平行,课本所在平面与桌面平行吗?从实践(1)(2)(3)中你可以得到什么结论?实例探究:实例探究:实例探究:实例探究: 定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.平面与平面平行判定定理抽象概括: (1)定义法:证明平面与平面无公共点; (2)判定定理: 怎样判定平面与平面平行?方法提炼:例1:平面?与平面?平行的条件可以是( )A. ?内有无穷多条直线都与?平行.B. 直线a//? , a // ?,且直线a不在?内,也不在?内.C. 直线a ì ? ,b ì ?,且a // ? ,b// ?D. ?内的任何直线与?平行.典型例题:D例2: 已知正方体ABCD-A1B1C1D1,求证:平面AB1D1//平面C1BD.典型例题 变式:已知正方体ABCD-A1B1C1D1,M、N、E、F分别是棱A1B1,A1D1,B1C1 ,C1D1的中点。求证:平面AMN//平面EFDB.例2、已知正方体ABCD-A1B1C1D1,
求证:平面AB1D1∥平面C1BD.分析:四边形ABC1D1为平行四边形.,即AD1∥BC1
同理四边形DBB1D1为平行四边形.即D1B1∥DB
变式:已知正方体ABCD-A1B1C1D1,M、N、E、F分别是棱A1B1,A1D1,B1C1 ,C1D1的中点。求证:平面AMN//平面EFDB.证明:∵M、N、 F 、 E分别为棱B1A1、A1D1、D1C1、C1B1的中点.NM 平面DBEF∴NEBA为平行四边形,∴AN∥BE,又∵AN∩NM=N∴平面AMN//平面EFDB又∵BE 平面DBEF如图,在正方体ABCD—A1B1C1D1中,E、F、G分别是棱BC、C1D1、 B1C1的中点。
求证(1)平面EFG//平面BDD1B1.
(2)EF//平面BDD1B1.试一试:2.应用判定定理判定面面平行时应注意:
两条相交直线小结:1.平面与平面平行的判定:3.应用判定定理判定面面平行的关键是找平行线方法一:三角形的中位线定理;方法二:平行四边形的平行关系。 线线平行 1 、想一想2、判断 面面平行 线面平行? 如果一个平面内有两条相交直线
分别平行于另一个平面内的两条相交
直线,那么这两个平面平行课外延伸:2、归纳平面与平面平行的判定定理推论 ?作业:A:小结
B:P62 A7
P52 B1(1)做模型,画直观图
(2)写过程,分“找”和“求”两步
