第一章 机械运动 核心专题1 速度的相关计算 学案 (含答案)2023-2024学年物理人教版八年级上册
文档属性
| 名称 | 第一章 机械运动 核心专题1 速度的相关计算 学案 (含答案)2023-2024学年物理人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 158.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-16 12:27:29 | ||
图片预览


文档简介
核心专题1 速度的相关计算
素养目标
1.训练常见的速度计算类型,总结计算题的解题技巧。
2.速度公式及其变形式的灵活运用。
◎重点:速度计算题的解题技巧。
【专题突破】
1.匀速直线运动速度的计算
例1 做匀速直线运动的物体,在8 s内通过了40 m的路程,则该物体在第4 s内的速度为 ( )
A.10 m/s B.5 m/s
C.2.5 m/s D.无法确定
思路导引 匀速直线运动是指物体沿着直线且快慢不变的运动,即在匀速直线运动中物体在任意时刻的速度都相等。v==5 m/s,所以第4 s内的速度也为5 m/s。
【答案】B
对点自测
1.做匀速直线运动的物体,在任意相等时间内通过的路程 (选填“相等”或“不相等”),若匀速运动的甲、乙两车在相同时间内经过的路程之比是2∶1,则速度之比是 。
【答案】1.相等 2∶1
2.平均速度的计算
例2 物体在做直线运动的过程中,如果速度大小随时间发生变化,则称为变速直线运动。若某物体沿直线以12 m/s的速度运动,通过了全程的,又以同方向16 m/s的速度通过了剩余的全部路程,则它全程的平均速度为 ( )
A.14.4 m/s B.15.4 m/s
C.14.33 m/s D.14.66 m/s
思路导引 根据题意先求出所对应路程的运动时间,然后由速度公式求出物体全程的平均速度。
【答案】A
对点自测
2.一个物体做直线运动,它在前2 s内的平均速度为6 m/s,后4 s内的平均速度为3 m/s,那么物体在6 s内的平均速度是 ( )
A.3 m/s B.4 m/s
C.4.5 m/s D.5 m/s
【答案】2.B
3.过桥类问题的计算
例3 周末,同学们排队步行去参加义务劳动,经过一座桥时,小红忽然想知道他们过桥的平均速度是多大,于是她通过测量知道了以下数据:队伍的长度为50 m,桥长为100 m,队伍过桥用了1 min。那么他们过桥的平均速度应为 ( )
A.2.5 m/s B.0.83 m/s
C.3.3 m/s D.1.67 m/s
思路导引 根据平均速度的计算方法,要求过桥的平均速度,就应知道该过程的总路程和总时间。总时间题中已给出,而队伍过桥时,要从队伍中的第一个人上桥到队伍中的最后一个人离桥为止,这个过程队伍通过的路程为队伍的长度加上桥的长度。
【答案】A
对点自测
3.一列火车的长度为240 m,以15 m/s的速度匀速通过长360 m的大桥。火车完全通过桥行驶的路程为 m,火车完全通过桥经历的时间为 s。
【答案】3.600 40
4.有关交通标志牌的计算
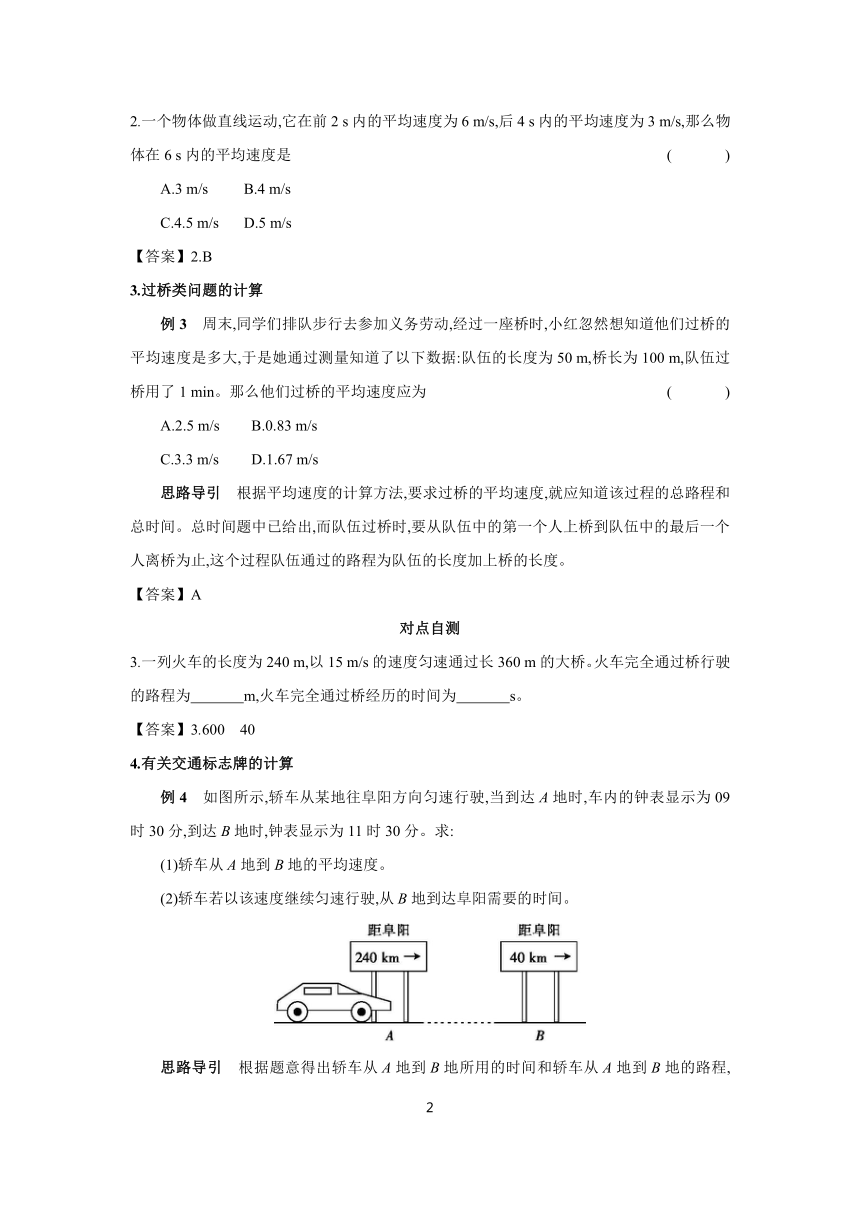
例4 如图所示,轿车从某地往阜阳方向匀速行驶,当到达A地时,车内的钟表显示为09时30分,到达B地时,钟表显示为11时30分。求:
(1)轿车从A地到B地的平均速度。
(2)轿车若以该速度继续匀速行驶,从B地到达阜阳需要的时间。
思路导引 根据题意得出轿车从A地到B地所用的时间和轿车从A地到B地的路程,利用v=求出轿车从A地到B地的速度;由图可知轿车从B地到阜阳的路程,轿车若以该速度继续匀速行驶,根据t=求出从B地到达阜阳需要的时间。
【答案】解:(1)轿车从A地到B地所用的时间t=11时30分-09时30分=2 h,由图知,轿车从A地到B地的路程s=240 km-40 km=200 km,则轿车从A地到B地的平均速度v===100 km/h。
(2)轿车从B地到阜阳的路程s'=40 km,轿车若以该速度继续匀速行驶,从B地到达阜阳需要的时间t'===0.4 h。
对点自测
4.章明同学和爸爸从县城驾车去小布镇游玩,车的速度表如图甲所示,他也看见路边一个交通标志牌,如图乙所示,问:
(1)该车的速度是多少
(2)该车以速度表上的速度行驶,从交通标志牌处到小布镇需要的时间为多少min
(3)该车在不违反交通规则的情况下,以最快的速度行驶,到达小布镇可以节约的时间为多少min
【答案】4.解:(1)由速度表可知,该车的速度为60 km/h。
(2)以速度表上的速度行驶,从标志牌上到小布镇需要的时间:t=== 0.15 h=9 min
(3)以最大速度行驶,从标志牌处到小布镇的时间:
t'===0.1125 h=6.75 min
可节约时间:Δt=t-t'=9 min-6.75 min=2.25 min
5.与图像有关的计算
例5 沿同一条直线向同一方向运动的物体A、B,运动时相对同一参考点O的距离s随时间t变化的图像如图所示。求:
(1)当t=5 s时,物体A和B的运动速度;
(2)当t=4 s时,物体A、B之间的距离。
思路导引 如s-t图像所示,分别在物体A、B的运动速度直线上选取适当的点,由公式v=计算物体A、B的运动速度;当t=4 s时,分别求得物体B相对参考点O的距离和物体A相对参考点O的距离。它们之间的差即物体A、B之间的距离。
【答案】解:(1)物体B的运动速度:
vB===1 m/s
物体A的运动速度:
vA===5 m/s
(2)当t=4 s时,物体B的运动路程为sB'=vBt=1 m/s×4 s=4 m;所以物体B相对参考点O的距离为4 m+5 m=9 m。物体A的运动路程为sA'=vAt'=5 m/s×(4 s-3 s)=5 m;所以物体A相对参考点O的距离为5 m,则物体A、B之间的距离为4 m。
对点自测
5.周末,小雨从家中到东湖公园锻炼,其中一半路程步行,一半路程骑自行车,路程与时间的图像如图所示。问:
(1)小雨从家中到东湖公园全程的平均速度是多少
(2)小雨步行的速度是多少
(3)若全程都用步行,要用多少时间
·方法突破·
计算题五步规范解题
(1)写“解:”;(2)用相应的符号列出已知条件(需要换算单位的换算好单位);(3)写出计算公式(或由原始公式得出需要的变形公式);(4)代入数据;(5)得出计算结果(注意一定要带单位)。
【答案】5.解:(1)由图知,全程的距离为s=1800 m,全程的时间t=20 min=1200 s,
全程的平均速度:
v===1.5 m/s
(2)前半程路程为s1=900 m,时间为t1=5 min=300 s,
前半程的速度:
v1===3 m/s
后半程的时间t2=20 min-5 min=15 min=900 s,
路程为s2=1800 m-900 m=900 m,
后半程的速度:
v2===1 m/s
因为3 m/s>1 m/s,所以骑车为前半程,步行为后半程,步行的速度为1 m/s。
(3)全程都用步行需要的时间:
t'===1800 s=30 min
解题指导
1.解答速度计算题的注意事项
速度的计算简单而基础,利用v=和变形公式s=vt、t=解题时,要注意下面几个问题:
(1)公式中的三个物理量必须是对于同一物体的同一个运动过程而言(同一题中不同物体、不同的运动过程要用下标区分,以免混淆),并且应统一物理量的单位。
(2)平均速度是指某段时间内物体运动的路程与它所用时间的比值,不是速度的平均值,这里运动的路程要和时间对应,不能“张冠李戴”。
(3)交通标志牌、列车(汽车等)时刻表、速度计等行程问题是提供解题条件的常见手段,解题时要明确各标志的含义,找到对解题有用的信息。
2.速度图像分析
(1)对s-t图像的理解:
如图所示,从图像可获取的信息有:①s与t成正比,即甲、乙做匀速运动;②甲图线的斜率大于乙的斜率,即甲的速度大于乙的速度;③相同的时间内,甲通过的路程大于乙通过的路程。
(2)对v-t图像的理解:
如图所示,从图像可获取的信息:①甲、乙图像中随着时间的推移,速度一直未发生变化,即可得出甲、乙做的都是匀速运动;②纵坐标中甲的图像居上,说明甲的速度大于乙的速度。
2
素养目标
1.训练常见的速度计算类型,总结计算题的解题技巧。
2.速度公式及其变形式的灵活运用。
◎重点:速度计算题的解题技巧。
【专题突破】
1.匀速直线运动速度的计算
例1 做匀速直线运动的物体,在8 s内通过了40 m的路程,则该物体在第4 s内的速度为 ( )
A.10 m/s B.5 m/s
C.2.5 m/s D.无法确定
思路导引 匀速直线运动是指物体沿着直线且快慢不变的运动,即在匀速直线运动中物体在任意时刻的速度都相等。v==5 m/s,所以第4 s内的速度也为5 m/s。
【答案】B
对点自测
1.做匀速直线运动的物体,在任意相等时间内通过的路程 (选填“相等”或“不相等”),若匀速运动的甲、乙两车在相同时间内经过的路程之比是2∶1,则速度之比是 。
【答案】1.相等 2∶1
2.平均速度的计算
例2 物体在做直线运动的过程中,如果速度大小随时间发生变化,则称为变速直线运动。若某物体沿直线以12 m/s的速度运动,通过了全程的,又以同方向16 m/s的速度通过了剩余的全部路程,则它全程的平均速度为 ( )
A.14.4 m/s B.15.4 m/s
C.14.33 m/s D.14.66 m/s
思路导引 根据题意先求出所对应路程的运动时间,然后由速度公式求出物体全程的平均速度。
【答案】A
对点自测
2.一个物体做直线运动,它在前2 s内的平均速度为6 m/s,后4 s内的平均速度为3 m/s,那么物体在6 s内的平均速度是 ( )
A.3 m/s B.4 m/s
C.4.5 m/s D.5 m/s
【答案】2.B
3.过桥类问题的计算
例3 周末,同学们排队步行去参加义务劳动,经过一座桥时,小红忽然想知道他们过桥的平均速度是多大,于是她通过测量知道了以下数据:队伍的长度为50 m,桥长为100 m,队伍过桥用了1 min。那么他们过桥的平均速度应为 ( )
A.2.5 m/s B.0.83 m/s
C.3.3 m/s D.1.67 m/s
思路导引 根据平均速度的计算方法,要求过桥的平均速度,就应知道该过程的总路程和总时间。总时间题中已给出,而队伍过桥时,要从队伍中的第一个人上桥到队伍中的最后一个人离桥为止,这个过程队伍通过的路程为队伍的长度加上桥的长度。
【答案】A
对点自测
3.一列火车的长度为240 m,以15 m/s的速度匀速通过长360 m的大桥。火车完全通过桥行驶的路程为 m,火车完全通过桥经历的时间为 s。
【答案】3.600 40
4.有关交通标志牌的计算
例4 如图所示,轿车从某地往阜阳方向匀速行驶,当到达A地时,车内的钟表显示为09时30分,到达B地时,钟表显示为11时30分。求:
(1)轿车从A地到B地的平均速度。
(2)轿车若以该速度继续匀速行驶,从B地到达阜阳需要的时间。
思路导引 根据题意得出轿车从A地到B地所用的时间和轿车从A地到B地的路程,利用v=求出轿车从A地到B地的速度;由图可知轿车从B地到阜阳的路程,轿车若以该速度继续匀速行驶,根据t=求出从B地到达阜阳需要的时间。
【答案】解:(1)轿车从A地到B地所用的时间t=11时30分-09时30分=2 h,由图知,轿车从A地到B地的路程s=240 km-40 km=200 km,则轿车从A地到B地的平均速度v===100 km/h。
(2)轿车从B地到阜阳的路程s'=40 km,轿车若以该速度继续匀速行驶,从B地到达阜阳需要的时间t'===0.4 h。
对点自测
4.章明同学和爸爸从县城驾车去小布镇游玩,车的速度表如图甲所示,他也看见路边一个交通标志牌,如图乙所示,问:
(1)该车的速度是多少
(2)该车以速度表上的速度行驶,从交通标志牌处到小布镇需要的时间为多少min
(3)该车在不违反交通规则的情况下,以最快的速度行驶,到达小布镇可以节约的时间为多少min
【答案】4.解:(1)由速度表可知,该车的速度为60 km/h。
(2)以速度表上的速度行驶,从标志牌上到小布镇需要的时间:t=== 0.15 h=9 min
(3)以最大速度行驶,从标志牌处到小布镇的时间:
t'===0.1125 h=6.75 min
可节约时间:Δt=t-t'=9 min-6.75 min=2.25 min
5.与图像有关的计算
例5 沿同一条直线向同一方向运动的物体A、B,运动时相对同一参考点O的距离s随时间t变化的图像如图所示。求:
(1)当t=5 s时,物体A和B的运动速度;
(2)当t=4 s时,物体A、B之间的距离。
思路导引 如s-t图像所示,分别在物体A、B的运动速度直线上选取适当的点,由公式v=计算物体A、B的运动速度;当t=4 s时,分别求得物体B相对参考点O的距离和物体A相对参考点O的距离。它们之间的差即物体A、B之间的距离。
【答案】解:(1)物体B的运动速度:
vB===1 m/s
物体A的运动速度:
vA===5 m/s
(2)当t=4 s时,物体B的运动路程为sB'=vBt=1 m/s×4 s=4 m;所以物体B相对参考点O的距离为4 m+5 m=9 m。物体A的运动路程为sA'=vAt'=5 m/s×(4 s-3 s)=5 m;所以物体A相对参考点O的距离为5 m,则物体A、B之间的距离为4 m。
对点自测
5.周末,小雨从家中到东湖公园锻炼,其中一半路程步行,一半路程骑自行车,路程与时间的图像如图所示。问:
(1)小雨从家中到东湖公园全程的平均速度是多少
(2)小雨步行的速度是多少
(3)若全程都用步行,要用多少时间
·方法突破·
计算题五步规范解题
(1)写“解:”;(2)用相应的符号列出已知条件(需要换算单位的换算好单位);(3)写出计算公式(或由原始公式得出需要的变形公式);(4)代入数据;(5)得出计算结果(注意一定要带单位)。
【答案】5.解:(1)由图知,全程的距离为s=1800 m,全程的时间t=20 min=1200 s,
全程的平均速度:
v===1.5 m/s
(2)前半程路程为s1=900 m,时间为t1=5 min=300 s,
前半程的速度:
v1===3 m/s
后半程的时间t2=20 min-5 min=15 min=900 s,
路程为s2=1800 m-900 m=900 m,
后半程的速度:
v2===1 m/s
因为3 m/s>1 m/s,所以骑车为前半程,步行为后半程,步行的速度为1 m/s。
(3)全程都用步行需要的时间:
t'===1800 s=30 min
解题指导
1.解答速度计算题的注意事项
速度的计算简单而基础,利用v=和变形公式s=vt、t=解题时,要注意下面几个问题:
(1)公式中的三个物理量必须是对于同一物体的同一个运动过程而言(同一题中不同物体、不同的运动过程要用下标区分,以免混淆),并且应统一物理量的单位。
(2)平均速度是指某段时间内物体运动的路程与它所用时间的比值,不是速度的平均值,这里运动的路程要和时间对应,不能“张冠李戴”。
(3)交通标志牌、列车(汽车等)时刻表、速度计等行程问题是提供解题条件的常见手段,解题时要明确各标志的含义,找到对解题有用的信息。
2.速度图像分析
(1)对s-t图像的理解:
如图所示,从图像可获取的信息有:①s与t成正比,即甲、乙做匀速运动;②甲图线的斜率大于乙的斜率,即甲的速度大于乙的速度;③相同的时间内,甲通过的路程大于乙通过的路程。
(2)对v-t图像的理解:
如图所示,从图像可获取的信息:①甲、乙图像中随着时间的推移,速度一直未发生变化,即可得出甲、乙做的都是匀速运动;②纵坐标中甲的图像居上,说明甲的速度大于乙的速度。
2
同课章节目录
- 科学之旅
- 第一章 机械运动
- 第1节 长度和时间的测量
- 第2节 运动的描述
- 第3节 运动的快慢
- 第4节 测量平均速度
- 第二章 声现象
- 第1节 声音的产生和传播
- 第2节 声音的特性
- 第3节 声的利用
- 第4节 噪声的危害和控制
- 第三章 物态变化
- 第1节 温度
- 第2节 熔化和凝固
- 第3节 汽化和液化
- 第4节 升华和凝华
- 第四章 光现象
- 第1节 光的直线传播
- 第2节 光的反射
- 第3节 平面镜成像
- 第4节 光的折射
- 第5节 光的色散
- 第五章 透镜及其应用
- 第1节 透镜
- 第2节 生活中的透镜
- 第3节 凸透镜成像的规律
- 第4节 眼睛和眼镜
- 第5节 显微镜和望远镜
- 第六章 质量和密度
- 第1节 质量
- 第2节 密度
- 第3节 测量物质的密度
- 第4节 密度与社会生活
