江苏省海门中学2023-2024学年高二下学期3月阶段练习数学试卷(含答案)
文档属性
| 名称 | 江苏省海门中学2023-2024学年高二下学期3月阶段练习数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 16:55:57 | ||
图片预览




文档简介
2023—2024学年度第二学期高二年级3月份阶段练习
数 学 试 题
一、单项选择题(本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.对于空间任一点和不共线的三点,,,有,则是,,,四点共面的
A.必要不充分条件 B.充分不必要条件 C.充要条件 D.既不充分又不必要条件
2.已知向量,向量在向量上的投影向量为
A. B. C. D.
3.中国古代中的“礼、乐、射、御、书、数”合称“六艺”。“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,指数学。某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“乐”和“书”两门课程相邻排课,则“六艺”课程讲座不同的排课顺序共有
A.240种 B.36种 C.120种 D.360种
4.“仁义礼智信”为儒家“五常”由孔子提出“仁、义、礼”,孟子延伸为“仁、义、礼、智”,董仲舒扩充为“仁、义、礼、智、信”。将“仁义礼智信”排成一排,其中“仁、义、礼”保持顺序不变的概率为
A. B. C. D.
5.在正四棱锥中,,与平面所成角为,则点到平面的距离为
A. B. C. D.
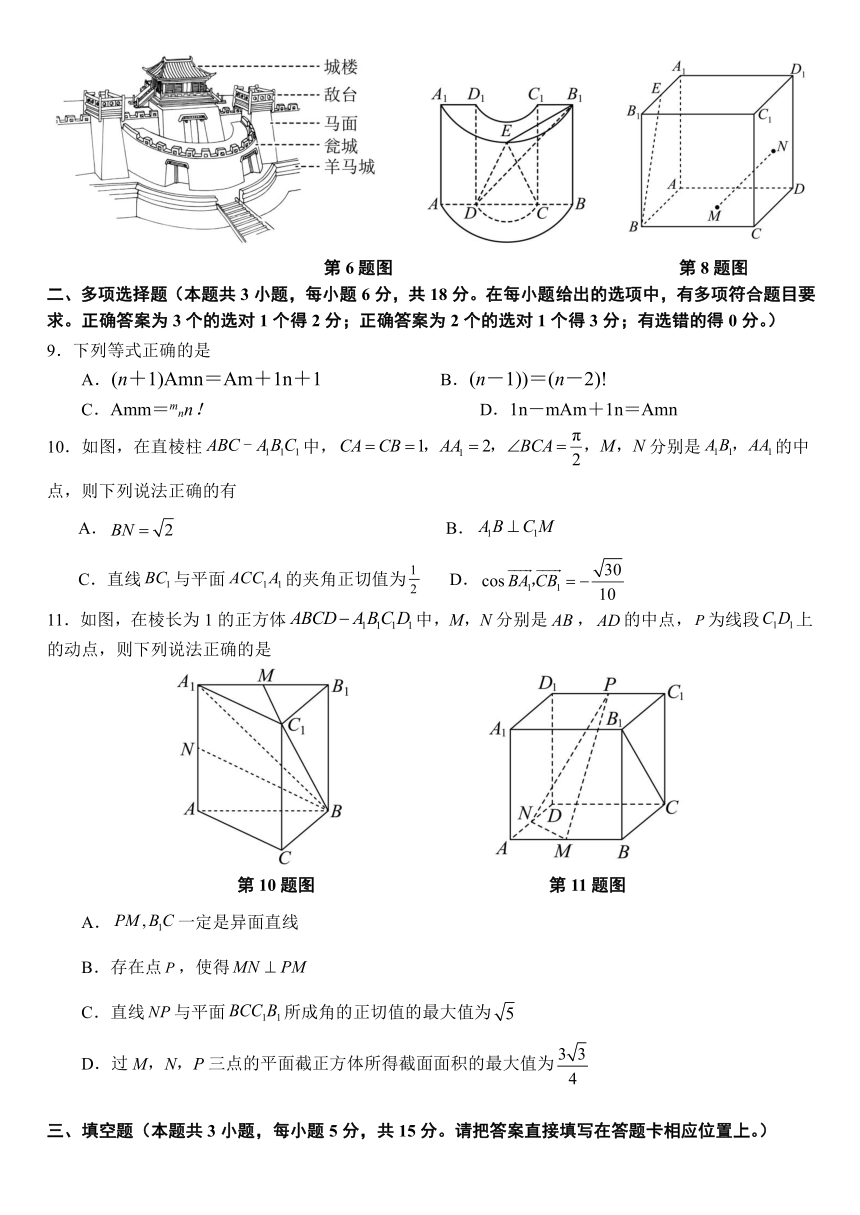
6.古代城池中的“瓮城”,又叫“曲池”,是加装在城门前面或里面的又一层门,若敌人攻入瓮城中,可形成“瓮中捉鳖”之势。如下图的“曲池”是上。下底面均为半圆形的柱体,若垂直于半圆柱下底面半圆所在平面,,,,为弧的中点,则直线与平面所成角的正弦值为
A. B. C. D.
7.2024年3月初,某运动队的7名队员合影留念,计划站成一横排,但甲不站最左端,乙不站最右端,丙不站正中间。则理论上他们的排法有
A.3864种 B.3216种 C.3144种 D.2952种
8.如图,在棱长为2的正方体中,为棱的中点,分别是底面与侧面的中心,为该正方体表面上的一个动点,且满足,记点的轨迹所在的平面为,则过四点的球面被平面截得的圆的周长是
A. B. C. D.
第6题图 第8题图
二、多项选择题(本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。正确答案为3个的选对1个得2分;正确答案为2个的选对1个得3分;有选错的得0分。)
9.下列等式正确的是
A.(n+1)Amn=Am+1n+1 B.n-1)=(n-2)!
C.Amm=mnn! D.1n-mAm+1n=Amn
10.如图,在直棱柱中,分别是的中点,则下列说法正确的有
A. B.
C.直线与平面的夹角正切值为 D.
11.如图,在棱长为1的正方体中,M,N分别是,的中点,为线段上的动点,则下列说法正确的是
第10题图 第11题图
A.一定是异面直线
B.存在点,使得
C.直线与平面所成角的正切值的最大值为
D.过M,N,P三点的平面截正方体所得截面面积的最大值为
三、填空题(本题共3小题,每小题5分,共15分。请把答案直接填写在答题卡相应位置上。)
12.已知三棱锥的体积为是空间中一点,,则三棱锥的体积是 .
13.中国古建筑闻名于世,源远流长.如图1所示的五脊殿是中国传统建筑中的一种屋顶形式,该屋顶的结构示意图可近似地看作如图2所示的五面体.现装修工人准备用四种不同形状的风铃装饰五脊殿的六个顶点,要求E,F处用同一种形状的风铃,其它每条棱的两个顶点挂不同形状的风铃,则不同的装饰方案共有 种。
14.在正方体中,,点平面,点F是线段的中点,若,则当的面积取得最小值时, .
四、解答题(本题共5小题,共77分。请在答题卡指定区域内作答。解答时应写出文字说明、证明过程或演算步骤。)
15.(本小题满分13分)已知向量,,
(1)求的值; (2)求; (3)求的最小值.
16.(本小题满分15分)用0,1,2,3,4这五个数字组成无重复数字的自然数.
(1)在组成的三位数中,求所有偶数的个数;
(2)在组成的三位数中,若十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301,423等都是“凹数”,试求“凹数”的个数;
(3)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数.
17.(本小题满分15分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)求证:BE⊥DC;
(2)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
18. (本小题满分17分)如图,是半球的直径,是底面半圆弧上的两个三等分点,是半球面上一点,且.
(1)证明:平面:
(2)若点在底面圆内的射影恰在上,求直线与平面所成角的正弦值.
19.(本小题满分17分)有个元素,将其中相同的元素归成一类,共有k类,这k类元素中每类分别中个,,将这个元素全部取出的排列叫做个不尽相异元素的全排列.
(1)求上述个不尽相异的元素的全排列数.
(2)由结论(1),回答“1个球队与10个球队各比赛1次,共有10场比赛,问五胜三负二平的可能情形有多少种?”
2023—2024学年度第二学期高二年级第一次联考
数 学 试 题 答 案
一、单项选择题。(本题共8小题,每小题5分,共40分。)
1.B 2.A 3.A 4.D 5.B 6.D 7.B 8.B
二、多项选择题。(本题共3小题,每小题6分,共18分。)
9.ABD 10.BC 11.AD
三、填空题。(本题共3小题,每小题5分,共15分。)
12. 10 13.72 14.
四、解答题。(本题共5小题,共77分。)
15.(1)因为,,所以,又因为,
所以.
(2)因为,,所以.
(3)因为,,所以,
所以,
当时,取得最小值,则最小值为.
16.(1)将组成的三位数中所有偶数分为两类:
①若个位数为0,则共有A24=12(个)符合题意的三位数;
②若个位数为2或4,则共有2×3×3=18(个)符合题意的三位数.
故共有12+18=30(个)符合题意的三位数.
(2)将这些“凹数”分为三类:
①若十位上的数字为0,则共有A24=12(个)符合题意的“凹数”;
②若十位上的数字为1,则共有A23=6(个)符合题意的“凹数”;
③若十位上的数字为2,则共有A22=2(个)符合题意的“凹数”.
故共有12+6+2=20(个)符合题意的“凹数”.
(3)将符合题意的五位数分为三类:
①若两个奇数数字在万位和百位上,则共有A22A33=12(个)符合题意的五位数;
②若两个奇数数字在千位和十位上,则共有A22A12A22=8(个)符合题意的五位数;
③若两个奇数数字在百位和个位上,则共有A22A12A22=8(个)符合题意的五位数.
故共有12+8+8=28(个)符合题意的五位数.
17.(1)证明 依题意,以点A为坐标原点建立空间直角坐标系(如图),可得A(0,0,0),
B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2).由E为棱PC的中点,得E(1,1,1),
所以=(0,1,1),=(2,0,0),故·=0,所以BE⊥DC.
(2)解 =(1,2,0),=(-2,-2,2),=(2,2,0),=(1,0,0).
由点F在棱PC上,设=λ(0≤λ≤1),
故=+=+λ=(1-2λ,2-2λ,2λ).由BF⊥AC,得·=0,
则2(1-2λ)+2(2-2λ)=0,解得λ=34,即=\a\vs4\al\co1(-\f(1132).设n1=(x,y,z)为平面FAB的法向量,
则n1·\o(AB→)BF→))=0即x=0,1132)z=0.不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量.
易知向量n2=(0,1,0)为平面ABP的一个法向量,则cos〈n1,n2〉=n1·n2|n1|·|n2|=-3\r(10)×1=-10)10.
由图可知,二面角F-AB-P为锐角,所以二面角F-AB-P的余弦值为10)10.
18.(1)连接,因为是底面半圆弧上的两个三等分点,所以有,又因为,所以都为正三角形,所以,四边形是菱形,记与的交点为,为和的中点,因为,所以三角形为正三角形,所以,所以,因为是半球面上一点,是半球的直径,所以,因为,平面,所以平面.
因为点在底面圆内的射影恰在上,由(1)知为的中点,为正三角形,所以,所以底面,因为四边形是菱形,所以,即两两互相垂直,以点为坐标原点,,,分别为,,轴,建立空间直角坐标系,如图所示, 则,
所以,,,设平面的一个法向量为
,则,所以,取,则,设直线与平面的所成角为,所以,故直线与平面所成角的正弦值为.
19.(1)假定个不尽相异元素的所有排列数有种,在每种排列中,如果把相同的元素,
当成不相同的元素,则个元素的所有排列数可增加为种;
另一方面,个不同的元素的全排列有种,∴即.
即得个不尽相异元素的全排列数.
(2)将比赛结果的胜、负、平看作三种元素,按题意,10场比赛的结果是五胜三负二平,
即是一个不尽相异元素的全排列,由(1)知,共有种可能情况.
2023—2024学年度第二学期高二年级3月份阶段练习
数 学 试 题 解 析
1.解:若,则,即,
由共面定理可知向量,,共面,所以,,,四点共面;反之,若,,,四点共面,当与四个点中的一个比如点重合时,,可取任意值,不一定有,所以是,,,四点共面的充分不必要条件.
2.解:因为向量,所以,
所以向量在向量上的投影向量为:
3.“乐”和“书”两门课程相邻排课,则“六艺”课程讲座不同的排课顺序共有排法.
4.选将“仁、义、礼”放好保持顺序不变,将“智”插空放入有4种方法,将“信”插空放入有5种方法,共有20种方法,将“仁义礼智信”排成一排共有种方法,因此将“仁义礼智信”排成一排,其中“仁、义、礼”保持顺序不变的概率为.
5.依题意,设,则平面,因为平面,所以为与平面所成角,即,因为,所以,则,以点为原点,建立空间直角坐标系如图,则,所以,
设平面的一个法向量为,则,
令,则,故,所以点到平面的距离为.
6.在半圆柱下底面半圆所在平面内过作直线的垂线,由于垂直于半圆柱下底面半圆所在平面,则以点为原点,建立如图所示的空间直角坐标系,于是,,又为的中点,则,,,,设平面的法向量,则,令,得,设直线与平面所成角为,则
,直线与平面所成角的正弦值为.
7.根据题意,分3种情况讨论:①、甲在右端,若乙在中间,则丙有5个位置可选,再将剩余的4个人全排列,安排在其余的4个位置,有种情况;甲在右端,若乙不在中间,则乙还有5个位置可选,此时丙还有4个位置可选,再将剩余的4个人全排列,安排在其余的4个位置, 有种情况;两种情况合并,共有种情况;②、若甲在中间,分丙在右端与丙不在右端两种,情况同①. 共有种情况;③、若甲不在中间也不在右端,先排甲,有4种方法,再排乙,乙若在中间,则丙有5种排法;乙若不在中间,则乙有4种排法,此时丙有4种排法;最后,将剩余的4个人全排列,安排在其余的4个位置,共有种情况;综上,则共有种不同的站法.
第5题解析图 第6题解析图 第8题解析图
8.取面对角线中点,连接,,,,分别在上,且,以为原点,的方向分别为轴,轴,轴正方向,建立如图所示的空间直角坐标系,
,,,, ,,,,,,,,,三棱锥中, 为直角三角形,所以,因此点即为三棱锥的外接球球心,球半径长为,,,,,,共面,
,,, ,平面,,平面,平面,点的轨迹为矩形的四边,如图所示,,为平面的法向量,则球心到平面的距离为,球面被平面截得的圆的半径,圆的周长为.
9.对于A,(n+1)Amn=(n+1)·n-m!)=n+1!,n-m!)=n+1!,[n+1-m+1]!)=Am+1n+1,正确;
对于B,n-1)=n-1n-2×…×3×2×1,nn-1)=(n-2)!正确;
对于C,Amm≠mnn!,错误;对于D,1n-mAm+1n=1n-m·n-m-1!)=n-m!)=Amn,正确.
10.对于A:因为,所以,则,A错误;对于B:因为,为线段中点,所以,又面面,面面,面,所以面,又面,所以,B正确;对于C:因为面,所以面,
所以为直线与平面的夹角,又,C正确;
对于D:
,又,
所以,D错误.
第11题解析图① 第11题解析图② 第12题解析图
11.以为坐标原点建立如图所示空间直角坐标系:
则,设,则点坐标为;
对A:设平面的法向量为,,
则,即,取,解得,故;
又,,考虑到,则,故,故一定是异面直线,A正确;对B:,,若,则,即,解得,又,故不存在这样的点,使得,B错误;对C: ,取平面的法向量,
则,设直线与平面的夹角为
则,则,
,又,故,即直线与平面所成角的正切值的最大值为,C错误;对D:在正方体中,过的截面为六边形且六边形为正六边形时面积最大.
此时过的截面经过对称中心,设截面交于中点,也为中点,
所以为的中点时,过三点的平面截正方体所得截面面积最大,
取的中点为,连接,如上所示:
故此时截面为正六边形,其面积,故D正确.
12.因为,则,
即,即,所以,因为,由空间向量基本定理可知,在平面内存在一点,使得成立,即,所以,即,则,又三棱锥的体积为15,则.
13.①使用3种形状风铃,只能同,同,同.此时共有:种挂法,
②使用4种形状风铃,此时有两种情况;1)同,不同:直接将4种风铃挂到四个点上,全排列有:种,2)不同,同:此时与1)相同,共有种。共24+24+24=72种.
14.以点D为坐标原点,以所在直线为轴,建立空间直角坐标系,
则,设,则,
因为,故,即,由于平面,平面,故,所以的面积为,
而,
故,当时,取最小值,即S最小,
此时,则,故,即
数 学 试 题
一、单项选择题(本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.对于空间任一点和不共线的三点,,,有,则是,,,四点共面的
A.必要不充分条件 B.充分不必要条件 C.充要条件 D.既不充分又不必要条件
2.已知向量,向量在向量上的投影向量为
A. B. C. D.
3.中国古代中的“礼、乐、射、御、书、数”合称“六艺”。“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,指数学。某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“乐”和“书”两门课程相邻排课,则“六艺”课程讲座不同的排课顺序共有
A.240种 B.36种 C.120种 D.360种
4.“仁义礼智信”为儒家“五常”由孔子提出“仁、义、礼”,孟子延伸为“仁、义、礼、智”,董仲舒扩充为“仁、义、礼、智、信”。将“仁义礼智信”排成一排,其中“仁、义、礼”保持顺序不变的概率为
A. B. C. D.
5.在正四棱锥中,,与平面所成角为,则点到平面的距离为
A. B. C. D.
6.古代城池中的“瓮城”,又叫“曲池”,是加装在城门前面或里面的又一层门,若敌人攻入瓮城中,可形成“瓮中捉鳖”之势。如下图的“曲池”是上。下底面均为半圆形的柱体,若垂直于半圆柱下底面半圆所在平面,,,,为弧的中点,则直线与平面所成角的正弦值为
A. B. C. D.
7.2024年3月初,某运动队的7名队员合影留念,计划站成一横排,但甲不站最左端,乙不站最右端,丙不站正中间。则理论上他们的排法有
A.3864种 B.3216种 C.3144种 D.2952种
8.如图,在棱长为2的正方体中,为棱的中点,分别是底面与侧面的中心,为该正方体表面上的一个动点,且满足,记点的轨迹所在的平面为,则过四点的球面被平面截得的圆的周长是
A. B. C. D.
第6题图 第8题图
二、多项选择题(本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。正确答案为3个的选对1个得2分;正确答案为2个的选对1个得3分;有选错的得0分。)
9.下列等式正确的是
A.(n+1)Amn=Am+1n+1 B.n-1)=(n-2)!
C.Amm=mnn! D.1n-mAm+1n=Amn
10.如图,在直棱柱中,分别是的中点,则下列说法正确的有
A. B.
C.直线与平面的夹角正切值为 D.
11.如图,在棱长为1的正方体中,M,N分别是,的中点,为线段上的动点,则下列说法正确的是
第10题图 第11题图
A.一定是异面直线
B.存在点,使得
C.直线与平面所成角的正切值的最大值为
D.过M,N,P三点的平面截正方体所得截面面积的最大值为
三、填空题(本题共3小题,每小题5分,共15分。请把答案直接填写在答题卡相应位置上。)
12.已知三棱锥的体积为是空间中一点,,则三棱锥的体积是 .
13.中国古建筑闻名于世,源远流长.如图1所示的五脊殿是中国传统建筑中的一种屋顶形式,该屋顶的结构示意图可近似地看作如图2所示的五面体.现装修工人准备用四种不同形状的风铃装饰五脊殿的六个顶点,要求E,F处用同一种形状的风铃,其它每条棱的两个顶点挂不同形状的风铃,则不同的装饰方案共有 种。
14.在正方体中,,点平面,点F是线段的中点,若,则当的面积取得最小值时, .
四、解答题(本题共5小题,共77分。请在答题卡指定区域内作答。解答时应写出文字说明、证明过程或演算步骤。)
15.(本小题满分13分)已知向量,,
(1)求的值; (2)求; (3)求的最小值.
16.(本小题满分15分)用0,1,2,3,4这五个数字组成无重复数字的自然数.
(1)在组成的三位数中,求所有偶数的个数;
(2)在组成的三位数中,若十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301,423等都是“凹数”,试求“凹数”的个数;
(3)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数.
17.(本小题满分15分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)求证:BE⊥DC;
(2)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
18. (本小题满分17分)如图,是半球的直径,是底面半圆弧上的两个三等分点,是半球面上一点,且.
(1)证明:平面:
(2)若点在底面圆内的射影恰在上,求直线与平面所成角的正弦值.
19.(本小题满分17分)有个元素,将其中相同的元素归成一类,共有k类,这k类元素中每类分别中个,,将这个元素全部取出的排列叫做个不尽相异元素的全排列.
(1)求上述个不尽相异的元素的全排列数.
(2)由结论(1),回答“1个球队与10个球队各比赛1次,共有10场比赛,问五胜三负二平的可能情形有多少种?”
2023—2024学年度第二学期高二年级第一次联考
数 学 试 题 答 案
一、单项选择题。(本题共8小题,每小题5分,共40分。)
1.B 2.A 3.A 4.D 5.B 6.D 7.B 8.B
二、多项选择题。(本题共3小题,每小题6分,共18分。)
9.ABD 10.BC 11.AD
三、填空题。(本题共3小题,每小题5分,共15分。)
12. 10 13.72 14.
四、解答题。(本题共5小题,共77分。)
15.(1)因为,,所以,又因为,
所以.
(2)因为,,所以.
(3)因为,,所以,
所以,
当时,取得最小值,则最小值为.
16.(1)将组成的三位数中所有偶数分为两类:
①若个位数为0,则共有A24=12(个)符合题意的三位数;
②若个位数为2或4,则共有2×3×3=18(个)符合题意的三位数.
故共有12+18=30(个)符合题意的三位数.
(2)将这些“凹数”分为三类:
①若十位上的数字为0,则共有A24=12(个)符合题意的“凹数”;
②若十位上的数字为1,则共有A23=6(个)符合题意的“凹数”;
③若十位上的数字为2,则共有A22=2(个)符合题意的“凹数”.
故共有12+6+2=20(个)符合题意的“凹数”.
(3)将符合题意的五位数分为三类:
①若两个奇数数字在万位和百位上,则共有A22A33=12(个)符合题意的五位数;
②若两个奇数数字在千位和十位上,则共有A22A12A22=8(个)符合题意的五位数;
③若两个奇数数字在百位和个位上,则共有A22A12A22=8(个)符合题意的五位数.
故共有12+8+8=28(个)符合题意的五位数.
17.(1)证明 依题意,以点A为坐标原点建立空间直角坐标系(如图),可得A(0,0,0),
B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2).由E为棱PC的中点,得E(1,1,1),
所以=(0,1,1),=(2,0,0),故·=0,所以BE⊥DC.
(2)解 =(1,2,0),=(-2,-2,2),=(2,2,0),=(1,0,0).
由点F在棱PC上,设=λ(0≤λ≤1),
故=+=+λ=(1-2λ,2-2λ,2λ).由BF⊥AC,得·=0,
则2(1-2λ)+2(2-2λ)=0,解得λ=34,即=\a\vs4\al\co1(-\f(1132).设n1=(x,y,z)为平面FAB的法向量,
则n1·\o(AB→)BF→))=0即x=0,1132)z=0.不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量.
易知向量n2=(0,1,0)为平面ABP的一个法向量,则cos〈n1,n2〉=n1·n2|n1|·|n2|=-3\r(10)×1=-10)10.
由图可知,二面角F-AB-P为锐角,所以二面角F-AB-P的余弦值为10)10.
18.(1)连接,因为是底面半圆弧上的两个三等分点,所以有,又因为,所以都为正三角形,所以,四边形是菱形,记与的交点为,为和的中点,因为,所以三角形为正三角形,所以,所以,因为是半球面上一点,是半球的直径,所以,因为,平面,所以平面.
因为点在底面圆内的射影恰在上,由(1)知为的中点,为正三角形,所以,所以底面,因为四边形是菱形,所以,即两两互相垂直,以点为坐标原点,,,分别为,,轴,建立空间直角坐标系,如图所示, 则,
所以,,,设平面的一个法向量为
,则,所以,取,则,设直线与平面的所成角为,所以,故直线与平面所成角的正弦值为.
19.(1)假定个不尽相异元素的所有排列数有种,在每种排列中,如果把相同的元素,
当成不相同的元素,则个元素的所有排列数可增加为种;
另一方面,个不同的元素的全排列有种,∴即.
即得个不尽相异元素的全排列数.
(2)将比赛结果的胜、负、平看作三种元素,按题意,10场比赛的结果是五胜三负二平,
即是一个不尽相异元素的全排列,由(1)知,共有种可能情况.
2023—2024学年度第二学期高二年级3月份阶段练习
数 学 试 题 解 析
1.解:若,则,即,
由共面定理可知向量,,共面,所以,,,四点共面;反之,若,,,四点共面,当与四个点中的一个比如点重合时,,可取任意值,不一定有,所以是,,,四点共面的充分不必要条件.
2.解:因为向量,所以,
所以向量在向量上的投影向量为:
3.“乐”和“书”两门课程相邻排课,则“六艺”课程讲座不同的排课顺序共有排法.
4.选将“仁、义、礼”放好保持顺序不变,将“智”插空放入有4种方法,将“信”插空放入有5种方法,共有20种方法,将“仁义礼智信”排成一排共有种方法,因此将“仁义礼智信”排成一排,其中“仁、义、礼”保持顺序不变的概率为.
5.依题意,设,则平面,因为平面,所以为与平面所成角,即,因为,所以,则,以点为原点,建立空间直角坐标系如图,则,所以,
设平面的一个法向量为,则,
令,则,故,所以点到平面的距离为.
6.在半圆柱下底面半圆所在平面内过作直线的垂线,由于垂直于半圆柱下底面半圆所在平面,则以点为原点,建立如图所示的空间直角坐标系,于是,,又为的中点,则,,,,设平面的法向量,则,令,得,设直线与平面所成角为,则
,直线与平面所成角的正弦值为.
7.根据题意,分3种情况讨论:①、甲在右端,若乙在中间,则丙有5个位置可选,再将剩余的4个人全排列,安排在其余的4个位置,有种情况;甲在右端,若乙不在中间,则乙还有5个位置可选,此时丙还有4个位置可选,再将剩余的4个人全排列,安排在其余的4个位置, 有种情况;两种情况合并,共有种情况;②、若甲在中间,分丙在右端与丙不在右端两种,情况同①. 共有种情况;③、若甲不在中间也不在右端,先排甲,有4种方法,再排乙,乙若在中间,则丙有5种排法;乙若不在中间,则乙有4种排法,此时丙有4种排法;最后,将剩余的4个人全排列,安排在其余的4个位置,共有种情况;综上,则共有种不同的站法.
第5题解析图 第6题解析图 第8题解析图
8.取面对角线中点,连接,,,,分别在上,且,以为原点,的方向分别为轴,轴,轴正方向,建立如图所示的空间直角坐标系,
,,,, ,,,,,,,,,三棱锥中, 为直角三角形,所以,因此点即为三棱锥的外接球球心,球半径长为,,,,,,共面,
,,, ,平面,,平面,平面,点的轨迹为矩形的四边,如图所示,,为平面的法向量,则球心到平面的距离为,球面被平面截得的圆的半径,圆的周长为.
9.对于A,(n+1)Amn=(n+1)·n-m!)=n+1!,n-m!)=n+1!,[n+1-m+1]!)=Am+1n+1,正确;
对于B,n-1)=n-1n-2×…×3×2×1,nn-1)=(n-2)!正确;
对于C,Amm≠mnn!,错误;对于D,1n-mAm+1n=1n-m·n-m-1!)=n-m!)=Amn,正确.
10.对于A:因为,所以,则,A错误;对于B:因为,为线段中点,所以,又面面,面面,面,所以面,又面,所以,B正确;对于C:因为面,所以面,
所以为直线与平面的夹角,又,C正确;
对于D:
,又,
所以,D错误.
第11题解析图① 第11题解析图② 第12题解析图
11.以为坐标原点建立如图所示空间直角坐标系:
则,设,则点坐标为;
对A:设平面的法向量为,,
则,即,取,解得,故;
又,,考虑到,则,故,故一定是异面直线,A正确;对B:,,若,则,即,解得,又,故不存在这样的点,使得,B错误;对C: ,取平面的法向量,
则,设直线与平面的夹角为
则,则,
,又,故,即直线与平面所成角的正切值的最大值为,C错误;对D:在正方体中,过的截面为六边形且六边形为正六边形时面积最大.
此时过的截面经过对称中心,设截面交于中点,也为中点,
所以为的中点时,过三点的平面截正方体所得截面面积最大,
取的中点为,连接,如上所示:
故此时截面为正六边形,其面积,故D正确.
12.因为,则,
即,即,所以,因为,由空间向量基本定理可知,在平面内存在一点,使得成立,即,所以,即,则,又三棱锥的体积为15,则.
13.①使用3种形状风铃,只能同,同,同.此时共有:种挂法,
②使用4种形状风铃,此时有两种情况;1)同,不同:直接将4种风铃挂到四个点上,全排列有:种,2)不同,同:此时与1)相同,共有种。共24+24+24=72种.
14.以点D为坐标原点,以所在直线为轴,建立空间直角坐标系,
则,设,则,
因为,故,即,由于平面,平面,故,所以的面积为,
而,
故,当时,取最小值,即S最小,
此时,则,故,即
同课章节目录
