【多媒体导学案】人教版数学九年级上册第22章第10课时二次函数与一元二次方程(2)(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第22章第10课时二次函数与一元二次方程(2)(教师版) |

|
|
| 格式 | doc | ||
| 文件大小 | 483.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-13 00:00:00 | ||
图片预览




文档简介
二次函数与一元二次方程(2)(教师版)
一、学习目标 1.了解图像法确定一元二次方程近似解的方 ( http: / / www.21cnjy.com )法;2.了解图像法解一元二次不等式的方法;3.体验函数y=ax2与y=bx+c的交点的横坐标是方程ax2=bx+c的解的探索过程,掌握用函数y=ax2和y=bx+c图像交点的方法求方程ax2=bx+c的解.
二、知识回顾 二次函数y=ax2+bx+c与一元二次方程的关系二次函数y=ax2+bx+c与x轴的交点横坐标就是一元二次方程ax2+bx+c=0的解.一元二次方程ax2+bx+c=0的根一元二次方程ax2+bx+c=0根的判别式(b2-4ac)有两个相异的实数根b2-4ac>0有两个相等的实数根b2-4ac=0没有实数根b2-4ac<0
三、新知讲解 1.利用二次函数的图象求一元二次方程的近似 ( http: / / www.21cnjy.com )根利用二次函数的图象求一元二次方程的近似根的一般步骤:(1)画出函数y=ax2+bx+c(a≠0)的图象;(2)确定抛物线与x轴的交点的个数,看交点在哪两个数之间;(3)列表,根据题目实际情况在两个数之间合 ( http: / / www.21cnjy.com )理等分,并用计算器估算每个等分点所对应的函数值y.当x由x1取到x2,对应的y值出现y1>0,y2<0(或 y1<0,y2>0)且符合题目近似值要求时,x1或x2可以看做方程的近似根.2.二次函数与一元二次不等式的关系设抛物线y=ax2+bx+c(a≠0)与x轴有两个交点A(x1,0),B(x2,0)(x1<x2),则当a>0时,不等式ax2+bx+c>0的解集是x<x1或x>x2,不等式ax2+bx+c<0的解集是x1<x<x2.
四.典例探究 扫一扫,有惊喜哦!1.图象法求一元二次方程的近似根【例1】利用二次函数图象求一元二次方程5x2+4x﹣2=0的近似根.总结:利用二次函数的图象求一元二次方程的近似根的一般步骤:(1)画出函数y=ax2+bx+c(a≠0)的图象;(2)确定抛物线与x轴的交点的个数,看交点在哪两个数之间;(3)列表,根据题目实际情 ( http: / / www.21cnjy.com )况在两个数之间合理等分,并用计算器估算每个等分点所对应的函数值y.当x由x1取到x2,对应的y值出现y1>0,y2<0(或 y1<0,y2>0)且符合题目近似值要求时,x1或x2可以看做方程的近似根.练1 利用函数y=x2﹣x﹣3的图象,借助计算器探索方程x2﹣x﹣3=0介于﹣3与﹣2之间的根(精确到0.1)2.图像法解一元二次不等式【例2】(2010 淮北模拟)阅读材料,解答问题.例:用图象法解一元二次不等式:x2﹣2x﹣3>0解:设y=x2﹣2x﹣3,则y是x的二次函数.∵a=1>0,∴抛物线开口向上.又∵当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3.∴由此得抛物线y=x2﹣2x﹣3的大致图象如图所示.观察函数图象可知:当x<﹣1或x>3时,y>0.∴x2﹣2x﹣3>0的解集是:x<﹣1或x>3.(1)观察图象,直接写出一元二次不等式:x2﹣2x﹣3>0的解集是__________;(2)仿照上例,用图象法解一元二次不等式:x2﹣1>0. ( http: / / www.21cnjy.com )总结:设抛物线y=ax2+bx+c(a ( http: / / www.21cnjy.com )≠0)与x轴有两个交点A(x1,0),B(x2,0)(x1<x2),则当a>0时,不等式ax2+bx+c>0的解集是x<x1或x>x2,不等式ax2+bx+c<0的解集是x1<x<x2.练2 画出函数y=﹣2x2+8x﹣6的图象,根据图象回答:(1)方程﹣2x2+8x﹣6=0的解是什么?(2)当x取何值时,y>0?(3)当x取何值时,y<0?3.用一次函数和二次函数图像交点的方法求一元二次方程的解【例3】已知二次函数y=2x2﹣2和一次函数y=5x+1.(1)你能用图象法求出方程2x2﹣2=5x+1的解吗?试试看;(2)请通过解方程的方法验证(1)问的解.总结:画出一次函数和二次函数的图象,观察两图象交点坐标,即可求相应一元二次方程的解.反过来,令二次函数和一次函数的值相等,列出关于x的一元二次方程,该一元二次方程的解即为二次函数与一次函数交点的横坐标.练3 利用函数图象求出一元二次方程 ( http: / / www.21cnjy.com )x2+2=4x的近似根,或在同一平面直角坐标系中画出二次函数y=x2+2和一次函数y=4x的图象,根据两个图象交点的横坐标找出一元二次方程x2+2=4x的近似根,请试一试.
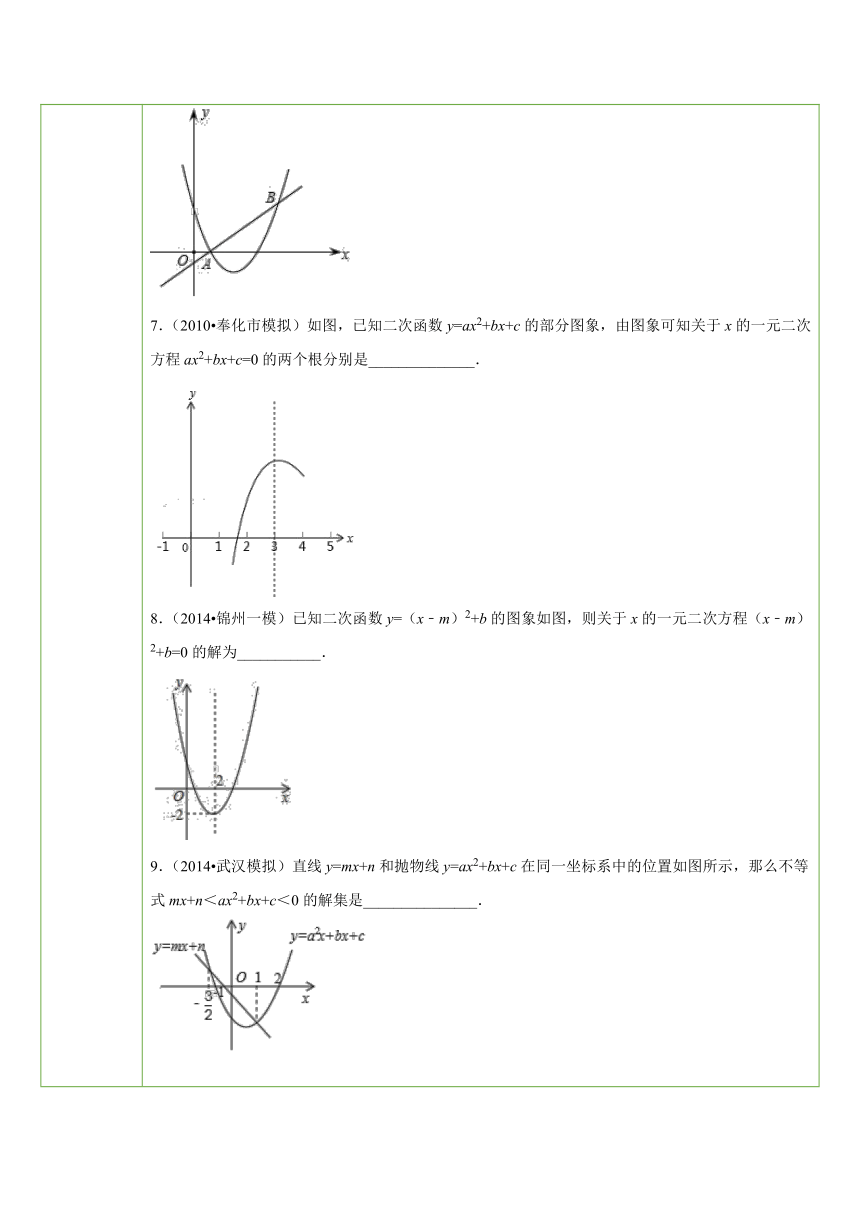
五、课后小测 一、选择题1.根据抛物线y=x2+3x﹣1与x轴的交点的坐标,可以求出下列方程中哪个方程的近似解( )A.x2﹣1=﹣3x B.x2+3x+1=0 C.3x2+x﹣1=0 D.x2﹣3x+1=02.(2014秋 安次区校级期中) ( http: / / www.21cnjy.com )已知:二次函数y=﹣x2﹣2x+m的部分图象如图所示,则关于x的一元二次方程﹣x2﹣2x+m=0的解为( ) ( http: / / www.21cnjy.com )A.1 B.3 C.2 D.03.(2015 泸州)若二次函数y=ax2+ ( http: / / www.21cnjy.com )bx+c(a<0)的图象经过点(2,0),且其对称轴为x=﹣1,则使函数值y>0成立的x的取值范围是( )A.x<﹣4或x>2 B.﹣4≤x≤2 C.x≤﹣4或x≥2 D.﹣4<x<24.(2015 成都模拟)已知二次函数y=x2﹣2x﹣1的图象如图所示,根据图中提供的信息,求使得y≤2成立的x的取值范围是( ) ( http: / / www.21cnjy.com )A.x≤﹣1或x≥3 B.﹣2≤x≤2 C.x≥﹣2 D.﹣1≤x≤35.(2014 尤溪县质检)直线y1=x+1与抛物线y2=﹣x2+3的图象如图,当y1>y2时,x的取值范围为( ) ( http: / / www.21cnjy.com )A.x<﹣2 B.x>1 C.﹣2<x<1 D.x<﹣2或x>1二、填空题6.(2015 大连模拟) ( http: / / www.21cnjy.com )如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2),不等式x2+bx+c>x+m 的解集为__________. ( http: / / www.21cnjy.com )7.(2010 奉化市模 ( http: / / www.21cnjy.com )拟)如图,已知二次函数y=ax2+bx+c的部分图象,由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是______________. ( http: / / www.21cnjy.com )8.(2014 锦州一模)已知二次函数 ( http: / / www.21cnjy.com )y=(x﹣m)2+b的图象如图,则关于x的一元二次方程(x﹣m)2+b=0的解为___________. ( http: / / www.21cnjy.com )9.(2014 武汉模拟)直线y=mx ( http: / / www.21cnjy.com )+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,那么不等式mx+n<ax2+bx+c<0的解集是_______________. ( http: / / www.21cnjy.com )三、解答题10.(2014 佛山)利用二次函数的图象估计一元二次方程x2﹣2x﹣1=0的近似根(精确到0.1).11.(2011 杭州模拟)小明在复习数学知识时,针对“求一元二次方程的解”整理了以下几种方法,请你将有关内容补充完整:例题:求一元二次方程x2﹣x﹣1=0的两个解.(1)解法一:选择合适的一种方法(公式法、配方法、分解因式法).(2)解法二:利用二次函数图象与两坐标轴的交点求解.如图,把方程x2﹣x﹣1=0的解看成是二次函数y=的图象与x轴交点的横坐标即x1,x2就是方程的解.(3)解法三:利用两个函数图象的交点求解①把方程x2﹣x﹣1=0的解看成是二次函数y=的图象与一个一次函数y=的图象交点的横坐标②画出这两个函数的图象,用x1,x2在x轴上标出方程的解. ( http: / / www.21cnjy.com )12.(2014 东西湖区校级模拟)如图,已知抛物线y1=﹣2x2+2与直线y2=2x+2交于A、B两点(1)求A、B两点的坐标.(2)若y1>y2,请直接写出x的取值范围. ( http: / / www.21cnjy.com )
13.一元二次方程x2+7x+9=1的根与二次函数y=x2+7x+9的图象有什么关系?试把方程的根在图象上表示出来.
典例探究答案:
【例1】【解析】根据函数与方程的关系,可得函数图象与x轴的交点的横坐标就是相应的方程的解.
解:方程5x2+4x﹣2=0根是函数y=5x2+4x﹣2与x轴交点的横坐标.
作出二次函数y=5x2+4x﹣2的图象,如图所示,
由图象可知方程有两个根,一个在﹣2和﹣1之间,另一个在0和1之间.
先求﹣2和﹣1之间的根,
当x=﹣1.1时,y=﹣0.35;当x=﹣1.2时,y=0.4;
因此,x=﹣1.15是方程的一个近似根,
同理,x=0.35是方程的另一个近似根.
故一元二次方程5x2+4x﹣2=0的近似根为x=﹣1.15或0.35.
( http: / / www.21cnjy.com )
点评:本题考查了图象法求一元二次方程的近似根,二次函数图象与x轴交点的横坐标是相应的一元二次方程的解.
练1.【解析】根据函数与方程的关系,可得函数图象与x轴的交点的横坐标就是相应的方程的解.
解:方程x2﹣x﹣3=0的根是函数y=x2﹣x﹣3与x轴交点的横坐标.
作出二次函数y=x2﹣x﹣3的图象,如图所示,
由图象可知方程有两个根,一个在﹣3与﹣2之间,另一个在2和3之间.
求﹣3与﹣2之间的根,
当x=﹣2.2时,y=﹣0.14;
当x=﹣2.3时,y=0.105;
因此,x=﹣2.3是方程介于﹣3与﹣2之间的一个近似根.
( http: / / www.21cnjy.com )
点评:本题考查了图象法求一元二次方程的近似根,解答此题的关键是求出对称轴,然后由图象解答,锻炼了学生数形结合的思想方法.
【例2】【解析】(1)由x2﹣2x ( http: / / www.21cnjy.com )﹣3=0得x1=﹣1,x2=3,抛物线y=x2﹣2x﹣3开口向上,y>0时,图象在x轴的上方,此时x<﹣1或x>3;
(2)仿照(1)的方法,画出函数y=x2﹣1的图象,找出图象与x轴的交点坐标,根据图象的开口方向及函数值的符号,确定x的范围.
解:(1)x<﹣1或x>3;
(2)设y=x2﹣1,则y是x的二次函数,
∵a=1>0,
∴抛物线开口向上.
又∵当y=0时,x2﹣1=0,
解得x1=﹣1,x2=1.
∴由此得抛物线y=x2﹣1的大致图象如图所示.
观察函数图象可知:当x<﹣1或x>1时,y>0.
∴x2﹣1>0的解集是:x<﹣1或x>1.
( http: / / www.21cnjy.com )
点评:本题考查了学生的阅读理解能力,知识 ( http: / / www.21cnjy.com )的迁移能力及二次函数与不等式的关系,解答此题的关键是求出图象与x轴的交点,然后由图象找出当y>0时,自变量x的范围.
练2.【解析】利用描点连线的方法画出函数y=﹣2x2+8x﹣6的图象.再根据图象判断函数的增减性.
解:函数y=﹣2x2+8x﹣6的图象如图.由图象可知:
(1)方程﹣2x2+8x﹣6=0的解x1=1,x2=3.
(2)当1<x<3时,y>0.
(3)当x<1或x>3时,y<0.
( http: / / www.21cnjy.com )
点评:本题重点考查了函数图象的画法及解读.
【例3】【解析】(1)根据函数图象的交点坐标是相应方程的解,可得答案;
(2)根据因式分解,可得方程的解.
解:(1)如图在平面直角坐标系内画出y=2x2﹣2和函数y=5x+1的图象,
( http: / / www.21cnjy.com )
图象交点的横坐标是﹣,3
2x2﹣2=5x+1的解是x1=﹣,x2=3;
(2)化简得
2x2﹣5x﹣3=0,
因式分解,得(2x+1)(x﹣3)=0.
解得x1=﹣,x2=3.
点评:本题考查了图象法求一元二次方程的近似根,图象交点的横坐标是方程的解.
练3.【解析】建立平面直角坐标系,根据网格结构作出函数y=x2+2和y=4x的图象,然后找出两函数图象的交点坐标,从而得解.
解:在同一平面直角坐标系中作出函数y=x2+2和y=4x的图象,如图所示:
( http: / / www.21cnjy.com )
由图可知,交点坐标为(0.6,2.4),(3.4,13.6),
所以一元二次方程x2+2=4x的近似根为x1≈0.6,x2≈3.4.
点评:本题考查了图象法求一元二次方程的近似根,主要是利用函数图象的交点坐标求方程的解,读懂题目信息是解题的关键.
课后小测答案:
一、选择题
1.【解析】根据抛物线y=x2+3x﹣1与x轴的交点的横坐标就是方程x2+3x﹣1=0的根来解决此题.
解:∵抛物线y=x2+3x﹣1与x轴的交点的横坐标就是方程x2+3x﹣1=0的根,
∴可以求出方程x2+3x﹣1=0的根,
方程x2﹣1=﹣3x与方程x2+3x﹣1=0等价,
∴可以求出方程x2﹣1=﹣3x的根.
故选A.
点评:据函数y=ax2+bx+c的图象与x轴的交点的横坐标就是方程ax2+bx+c=0的根.
2.【解析】根据二次函数的图象得出抛物线与x轴的交点,进而可得出结论.
解:∵由图可知,抛物线的对称轴为x=﹣1,抛物线与x轴的一个交点为﹣3,
∴另一个交点=2×(﹣1)+3=1,
∴关于x的一元二次方程﹣x2﹣2x+m=0的解为x1=﹣3,x2=1.
故选A.
点评:本题考查的是抛物线与x轴的交点 ( http: / / www.21cnjy.com )问题,熟知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系是解答此题的关键.
3.【解析】由抛物线与x轴的交点及对称轴求出另一个交点坐标,根据抛物线开口向下,根据图象求出使函数值y>0成立的x的取值范围即可.
解:∵二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=﹣1,
∴二次函数的图象与x轴另一个交点为(﹣4,0),
∵a<0,
∴抛物线开口向下,
则使函数值y>0成立的x的取值范围是﹣4<x<2.
故选D.
点评:此题考查了二次函数与不等式(组),求出抛物线与x轴另一个交点坐标是解本题的关键.
4.【解析】根据函数图象写出y=2对应的自变量x的值之间的取值即可.
解:由图可知,使得y≤2成立的x的取值范围是﹣1≤x≤3.
故选D.
点评:本题考查了二次函数与不等式,准确识图是解题的关键.
5.【解析】根据函数图象,写出直线在抛物线上方部分的x的取值范围即可.
解:由图可知,x<﹣2或x>1时,y1>y2.
故选D.
点评:本题考查了二次函数与不等式,此类题目,利用数形结合的思想求解是解题的关键.
二、填空题
6.【解析】根据已知条件和图象找出直线y=x+m和抛物线y=x2+bx+c的交点,即可求出不等式x2+bx+c>x+m 的解集.
解:∵直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2),
∴根据图象可知,不等式x2+bx+c>x+m 的解集为x<1或x>3;
故答案为:x<1或x>3.
点评:主要考查了二次函数与不等式组,解题的关键是根据图象找出直线y=x+m和抛物线y=x2+bx+c的交点,要具备读图的能力.
7.【解析】本题是一道估算题,先测估计出对称轴左侧图象与x轴交点的横坐标,再利用对称轴x=3,可以算出右侧交点横坐标.
解:依题意得二次函数y=ax2+bx+c的部分图象的对称轴为x=3,
而对称轴左侧图象与x轴交点与原点的距离,约为1.6,
∴x1=1.6;
又∵对称轴为x=3,
则=3,
∴x2=2×3﹣1.6=4.4.
点评:解答本题首先需要估计图象估计出一个解,再根据对称性计算出另一个解,估计值的精确程度,直接关系到计算的准确性,必须估计尽量准确.
8.【解析】二次函数y=(x﹣m)2+ ( http: / / www.21cnjy.com )b的顶点坐标为(m,b),由图象得,m=2,b=﹣2,可得二次函数的解析式为y=(x﹣2)2﹣2.再解一元二次方程即可.
解:由图象得,m=2,b=﹣2,
所以二次函数的解析式为y=(x﹣2)2﹣2.
关于x的一元二次方程(x﹣2)2﹣2=0
(x﹣2)2=2
解得:,.
故答案为:,.
点评:本题主要考查了抛物线与x轴的交点问题,本题的关键是得出二次函数的解析式为y=(x﹣2)2﹣2.
9.【解析】从图上可知,mx+n<ax2+bx+c,则有x>1或x<﹣;根据ax2+bx+c<0,可知﹣1<x<2;综上,不等式mx+n<ax2+bx+c<0的解集是1<x<2.
解:因为mx+n<ax2+bx+c<0,由图可知,1<x<2.
点评:此题将图形与不等式相结合,考查了同学们对不等式组的解集的理解和读图能力,有一定的难度,读图时要仔细.
三、解答题
10.【解析】根据函数与方程的关系,可得函数图象与x轴的交点的横坐标就是相应的方程的解.
解:方程x2﹣2x﹣1=0根是函数y=x2﹣2x﹣1与x轴交点的横坐标.
作出二次函数y=x2﹣2x﹣1的图象,如图所示,
由图象可知方程有两个根,一个在﹣1和0之间,另一个在2和3之间.
先求﹣1和0之间的根,
当x=﹣0.4时,y=﹣0.04;当x=﹣0.5时,y=0.25;
因此,x=﹣0.4(或x=﹣0.5)是方程的一个近似根,
同理,x=2.4(或x=2.5)是方程的另一个近似根.
( http: / / www.21cnjy.com )
点评:本题考查了图象法求一元二次方程的近似值,解答此题的关键是求出对称轴,然后由图象解答,锻炼了学生数形结合的思想方法.
11.【解析】(1)用配方法解答一元二次方程;
(2)二次函数方程为y=ax2 ( http: / / www.21cnjy.com )+bx+c与x轴交点的横坐标就是方程x2﹣x﹣1=0的解,所以,只要求出方程x2﹣x﹣1=0的根,就可以求出二次函数方程为y=ax2+bx+c与x轴交点;
(3)由(1)(2)解得x1、x2,再根据题意画出图象.
解:(1)由原方程,得:
,即;
解得x1= ,x2=.
(2)设二次函数方程为y=ax2+bx+c(a,b,c均为实数,且a≠0).
由图象得知,该函数过点(0,﹣1),所以该点满足方程y=ax2+bx+c,
∴把(0,﹣1)代入方程y=ax2+bx+c,得c=﹣1,①
二次函数方程为y=ax2+bx+c与x轴交点的横坐标就是方程x2﹣x﹣1=0的解;
∴x1 x2==﹣1,即c=﹣a;②
x1+x2==1;③
由①②③,得:
;
∴二次函数方程为y=x2﹣x﹣1.
(3)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
点评:本题考查的是二次函数与一元二次方程,在解答过程中,注意二次函数与一元二次方程之间的联系,并从中择取有用信息解题.
12.【解析】(1)联立两函数解析式求解即可;
(2)根据函数图象写出抛物线直线上方部分的x的取值范围即可.
解:(1)联立,
解得: 或,
所以A、B两点的坐标分别是(﹣1,0),(0,2);
(2)由图可知,﹣<x<0时,y1>y2.
点评:本题考查二次函数与不等式,主要利用了联立两函数解析式求交点坐标的方法,利用函数图象求不等式的解集,利用数形结合的思想求解是更简便.
13.【解析】画出二次函数y=x2+7x+9的图象,则一元二次方程x2+7x+9=1的根为图象中y=1时x的值.
解:一元二次方程x2+7x+9=1的根是二次函数y=x2+7x+9图象中y=1时,所对应的x的值;
当y=1时,x2+7x+9=1,
∴作出二次函数y=x2+7x+9的图象如图,由图中可以看出,当y=1时,x≈﹣5.6或﹣1.4,
∴一元二次方程x2+7x+9=1的根为x1≈﹣5.6,x2≈﹣1.4.
( http: / / www.21cnjy.com )
点评:考查二次函数图象与一元二次方程近似跟的关系;关键是得到一元二次方程的图象;难点是判断出一元二次方程的根在图象中的位置.
一、学习目标 1.了解图像法确定一元二次方程近似解的方 ( http: / / www.21cnjy.com )法;2.了解图像法解一元二次不等式的方法;3.体验函数y=ax2与y=bx+c的交点的横坐标是方程ax2=bx+c的解的探索过程,掌握用函数y=ax2和y=bx+c图像交点的方法求方程ax2=bx+c的解.
二、知识回顾 二次函数y=ax2+bx+c与一元二次方程的关系二次函数y=ax2+bx+c与x轴的交点横坐标就是一元二次方程ax2+bx+c=0的解.一元二次方程ax2+bx+c=0的根一元二次方程ax2+bx+c=0根的判别式(b2-4ac)有两个相异的实数根b2-4ac>0有两个相等的实数根b2-4ac=0没有实数根b2-4ac<0
三、新知讲解 1.利用二次函数的图象求一元二次方程的近似 ( http: / / www.21cnjy.com )根利用二次函数的图象求一元二次方程的近似根的一般步骤:(1)画出函数y=ax2+bx+c(a≠0)的图象;(2)确定抛物线与x轴的交点的个数,看交点在哪两个数之间;(3)列表,根据题目实际情况在两个数之间合 ( http: / / www.21cnjy.com )理等分,并用计算器估算每个等分点所对应的函数值y.当x由x1取到x2,对应的y值出现y1>0,y2<0(或 y1<0,y2>0)且符合题目近似值要求时,x1或x2可以看做方程的近似根.2.二次函数与一元二次不等式的关系设抛物线y=ax2+bx+c(a≠0)与x轴有两个交点A(x1,0),B(x2,0)(x1<x2),则当a>0时,不等式ax2+bx+c>0的解集是x<x1或x>x2,不等式ax2+bx+c<0的解集是x1<x<x2.
四.典例探究 扫一扫,有惊喜哦!1.图象法求一元二次方程的近似根【例1】利用二次函数图象求一元二次方程5x2+4x﹣2=0的近似根.总结:利用二次函数的图象求一元二次方程的近似根的一般步骤:(1)画出函数y=ax2+bx+c(a≠0)的图象;(2)确定抛物线与x轴的交点的个数,看交点在哪两个数之间;(3)列表,根据题目实际情 ( http: / / www.21cnjy.com )况在两个数之间合理等分,并用计算器估算每个等分点所对应的函数值y.当x由x1取到x2,对应的y值出现y1>0,y2<0(或 y1<0,y2>0)且符合题目近似值要求时,x1或x2可以看做方程的近似根.练1 利用函数y=x2﹣x﹣3的图象,借助计算器探索方程x2﹣x﹣3=0介于﹣3与﹣2之间的根(精确到0.1)2.图像法解一元二次不等式【例2】(2010 淮北模拟)阅读材料,解答问题.例:用图象法解一元二次不等式:x2﹣2x﹣3>0解:设y=x2﹣2x﹣3,则y是x的二次函数.∵a=1>0,∴抛物线开口向上.又∵当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3.∴由此得抛物线y=x2﹣2x﹣3的大致图象如图所示.观察函数图象可知:当x<﹣1或x>3时,y>0.∴x2﹣2x﹣3>0的解集是:x<﹣1或x>3.(1)观察图象,直接写出一元二次不等式:x2﹣2x﹣3>0的解集是__________;(2)仿照上例,用图象法解一元二次不等式:x2﹣1>0. ( http: / / www.21cnjy.com )总结:设抛物线y=ax2+bx+c(a ( http: / / www.21cnjy.com )≠0)与x轴有两个交点A(x1,0),B(x2,0)(x1<x2),则当a>0时,不等式ax2+bx+c>0的解集是x<x1或x>x2,不等式ax2+bx+c<0的解集是x1<x<x2.练2 画出函数y=﹣2x2+8x﹣6的图象,根据图象回答:(1)方程﹣2x2+8x﹣6=0的解是什么?(2)当x取何值时,y>0?(3)当x取何值时,y<0?3.用一次函数和二次函数图像交点的方法求一元二次方程的解【例3】已知二次函数y=2x2﹣2和一次函数y=5x+1.(1)你能用图象法求出方程2x2﹣2=5x+1的解吗?试试看;(2)请通过解方程的方法验证(1)问的解.总结:画出一次函数和二次函数的图象,观察两图象交点坐标,即可求相应一元二次方程的解.反过来,令二次函数和一次函数的值相等,列出关于x的一元二次方程,该一元二次方程的解即为二次函数与一次函数交点的横坐标.练3 利用函数图象求出一元二次方程 ( http: / / www.21cnjy.com )x2+2=4x的近似根,或在同一平面直角坐标系中画出二次函数y=x2+2和一次函数y=4x的图象,根据两个图象交点的横坐标找出一元二次方程x2+2=4x的近似根,请试一试.
五、课后小测 一、选择题1.根据抛物线y=x2+3x﹣1与x轴的交点的坐标,可以求出下列方程中哪个方程的近似解( )A.x2﹣1=﹣3x B.x2+3x+1=0 C.3x2+x﹣1=0 D.x2﹣3x+1=02.(2014秋 安次区校级期中) ( http: / / www.21cnjy.com )已知:二次函数y=﹣x2﹣2x+m的部分图象如图所示,则关于x的一元二次方程﹣x2﹣2x+m=0的解为( ) ( http: / / www.21cnjy.com )A.1 B.3 C.2 D.03.(2015 泸州)若二次函数y=ax2+ ( http: / / www.21cnjy.com )bx+c(a<0)的图象经过点(2,0),且其对称轴为x=﹣1,则使函数值y>0成立的x的取值范围是( )A.x<﹣4或x>2 B.﹣4≤x≤2 C.x≤﹣4或x≥2 D.﹣4<x<24.(2015 成都模拟)已知二次函数y=x2﹣2x﹣1的图象如图所示,根据图中提供的信息,求使得y≤2成立的x的取值范围是( ) ( http: / / www.21cnjy.com )A.x≤﹣1或x≥3 B.﹣2≤x≤2 C.x≥﹣2 D.﹣1≤x≤35.(2014 尤溪县质检)直线y1=x+1与抛物线y2=﹣x2+3的图象如图,当y1>y2时,x的取值范围为( ) ( http: / / www.21cnjy.com )A.x<﹣2 B.x>1 C.﹣2<x<1 D.x<﹣2或x>1二、填空题6.(2015 大连模拟) ( http: / / www.21cnjy.com )如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2),不等式x2+bx+c>x+m 的解集为__________. ( http: / / www.21cnjy.com )7.(2010 奉化市模 ( http: / / www.21cnjy.com )拟)如图,已知二次函数y=ax2+bx+c的部分图象,由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是______________. ( http: / / www.21cnjy.com )8.(2014 锦州一模)已知二次函数 ( http: / / www.21cnjy.com )y=(x﹣m)2+b的图象如图,则关于x的一元二次方程(x﹣m)2+b=0的解为___________. ( http: / / www.21cnjy.com )9.(2014 武汉模拟)直线y=mx ( http: / / www.21cnjy.com )+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,那么不等式mx+n<ax2+bx+c<0的解集是_______________. ( http: / / www.21cnjy.com )三、解答题10.(2014 佛山)利用二次函数的图象估计一元二次方程x2﹣2x﹣1=0的近似根(精确到0.1).11.(2011 杭州模拟)小明在复习数学知识时,针对“求一元二次方程的解”整理了以下几种方法,请你将有关内容补充完整:例题:求一元二次方程x2﹣x﹣1=0的两个解.(1)解法一:选择合适的一种方法(公式法、配方法、分解因式法).(2)解法二:利用二次函数图象与两坐标轴的交点求解.如图,把方程x2﹣x﹣1=0的解看成是二次函数y=的图象与x轴交点的横坐标即x1,x2就是方程的解.(3)解法三:利用两个函数图象的交点求解①把方程x2﹣x﹣1=0的解看成是二次函数y=的图象与一个一次函数y=的图象交点的横坐标②画出这两个函数的图象,用x1,x2在x轴上标出方程的解. ( http: / / www.21cnjy.com )12.(2014 东西湖区校级模拟)如图,已知抛物线y1=﹣2x2+2与直线y2=2x+2交于A、B两点(1)求A、B两点的坐标.(2)若y1>y2,请直接写出x的取值范围. ( http: / / www.21cnjy.com )
13.一元二次方程x2+7x+9=1的根与二次函数y=x2+7x+9的图象有什么关系?试把方程的根在图象上表示出来.
典例探究答案:
【例1】【解析】根据函数与方程的关系,可得函数图象与x轴的交点的横坐标就是相应的方程的解.
解:方程5x2+4x﹣2=0根是函数y=5x2+4x﹣2与x轴交点的横坐标.
作出二次函数y=5x2+4x﹣2的图象,如图所示,
由图象可知方程有两个根,一个在﹣2和﹣1之间,另一个在0和1之间.
先求﹣2和﹣1之间的根,
当x=﹣1.1时,y=﹣0.35;当x=﹣1.2时,y=0.4;
因此,x=﹣1.15是方程的一个近似根,
同理,x=0.35是方程的另一个近似根.
故一元二次方程5x2+4x﹣2=0的近似根为x=﹣1.15或0.35.
( http: / / www.21cnjy.com )
点评:本题考查了图象法求一元二次方程的近似根,二次函数图象与x轴交点的横坐标是相应的一元二次方程的解.
练1.【解析】根据函数与方程的关系,可得函数图象与x轴的交点的横坐标就是相应的方程的解.
解:方程x2﹣x﹣3=0的根是函数y=x2﹣x﹣3与x轴交点的横坐标.
作出二次函数y=x2﹣x﹣3的图象,如图所示,
由图象可知方程有两个根,一个在﹣3与﹣2之间,另一个在2和3之间.
求﹣3与﹣2之间的根,
当x=﹣2.2时,y=﹣0.14;
当x=﹣2.3时,y=0.105;
因此,x=﹣2.3是方程介于﹣3与﹣2之间的一个近似根.
( http: / / www.21cnjy.com )
点评:本题考查了图象法求一元二次方程的近似根,解答此题的关键是求出对称轴,然后由图象解答,锻炼了学生数形结合的思想方法.
【例2】【解析】(1)由x2﹣2x ( http: / / www.21cnjy.com )﹣3=0得x1=﹣1,x2=3,抛物线y=x2﹣2x﹣3开口向上,y>0时,图象在x轴的上方,此时x<﹣1或x>3;
(2)仿照(1)的方法,画出函数y=x2﹣1的图象,找出图象与x轴的交点坐标,根据图象的开口方向及函数值的符号,确定x的范围.
解:(1)x<﹣1或x>3;
(2)设y=x2﹣1,则y是x的二次函数,
∵a=1>0,
∴抛物线开口向上.
又∵当y=0时,x2﹣1=0,
解得x1=﹣1,x2=1.
∴由此得抛物线y=x2﹣1的大致图象如图所示.
观察函数图象可知:当x<﹣1或x>1时,y>0.
∴x2﹣1>0的解集是:x<﹣1或x>1.
( http: / / www.21cnjy.com )
点评:本题考查了学生的阅读理解能力,知识 ( http: / / www.21cnjy.com )的迁移能力及二次函数与不等式的关系,解答此题的关键是求出图象与x轴的交点,然后由图象找出当y>0时,自变量x的范围.
练2.【解析】利用描点连线的方法画出函数y=﹣2x2+8x﹣6的图象.再根据图象判断函数的增减性.
解:函数y=﹣2x2+8x﹣6的图象如图.由图象可知:
(1)方程﹣2x2+8x﹣6=0的解x1=1,x2=3.
(2)当1<x<3时,y>0.
(3)当x<1或x>3时,y<0.
( http: / / www.21cnjy.com )
点评:本题重点考查了函数图象的画法及解读.
【例3】【解析】(1)根据函数图象的交点坐标是相应方程的解,可得答案;
(2)根据因式分解,可得方程的解.
解:(1)如图在平面直角坐标系内画出y=2x2﹣2和函数y=5x+1的图象,
( http: / / www.21cnjy.com )
图象交点的横坐标是﹣,3
2x2﹣2=5x+1的解是x1=﹣,x2=3;
(2)化简得
2x2﹣5x﹣3=0,
因式分解,得(2x+1)(x﹣3)=0.
解得x1=﹣,x2=3.
点评:本题考查了图象法求一元二次方程的近似根,图象交点的横坐标是方程的解.
练3.【解析】建立平面直角坐标系,根据网格结构作出函数y=x2+2和y=4x的图象,然后找出两函数图象的交点坐标,从而得解.
解:在同一平面直角坐标系中作出函数y=x2+2和y=4x的图象,如图所示:
( http: / / www.21cnjy.com )
由图可知,交点坐标为(0.6,2.4),(3.4,13.6),
所以一元二次方程x2+2=4x的近似根为x1≈0.6,x2≈3.4.
点评:本题考查了图象法求一元二次方程的近似根,主要是利用函数图象的交点坐标求方程的解,读懂题目信息是解题的关键.
课后小测答案:
一、选择题
1.【解析】根据抛物线y=x2+3x﹣1与x轴的交点的横坐标就是方程x2+3x﹣1=0的根来解决此题.
解:∵抛物线y=x2+3x﹣1与x轴的交点的横坐标就是方程x2+3x﹣1=0的根,
∴可以求出方程x2+3x﹣1=0的根,
方程x2﹣1=﹣3x与方程x2+3x﹣1=0等价,
∴可以求出方程x2﹣1=﹣3x的根.
故选A.
点评:据函数y=ax2+bx+c的图象与x轴的交点的横坐标就是方程ax2+bx+c=0的根.
2.【解析】根据二次函数的图象得出抛物线与x轴的交点,进而可得出结论.
解:∵由图可知,抛物线的对称轴为x=﹣1,抛物线与x轴的一个交点为﹣3,
∴另一个交点=2×(﹣1)+3=1,
∴关于x的一元二次方程﹣x2﹣2x+m=0的解为x1=﹣3,x2=1.
故选A.
点评:本题考查的是抛物线与x轴的交点 ( http: / / www.21cnjy.com )问题,熟知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系是解答此题的关键.
3.【解析】由抛物线与x轴的交点及对称轴求出另一个交点坐标,根据抛物线开口向下,根据图象求出使函数值y>0成立的x的取值范围即可.
解:∵二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=﹣1,
∴二次函数的图象与x轴另一个交点为(﹣4,0),
∵a<0,
∴抛物线开口向下,
则使函数值y>0成立的x的取值范围是﹣4<x<2.
故选D.
点评:此题考查了二次函数与不等式(组),求出抛物线与x轴另一个交点坐标是解本题的关键.
4.【解析】根据函数图象写出y=2对应的自变量x的值之间的取值即可.
解:由图可知,使得y≤2成立的x的取值范围是﹣1≤x≤3.
故选D.
点评:本题考查了二次函数与不等式,准确识图是解题的关键.
5.【解析】根据函数图象,写出直线在抛物线上方部分的x的取值范围即可.
解:由图可知,x<﹣2或x>1时,y1>y2.
故选D.
点评:本题考查了二次函数与不等式,此类题目,利用数形结合的思想求解是解题的关键.
二、填空题
6.【解析】根据已知条件和图象找出直线y=x+m和抛物线y=x2+bx+c的交点,即可求出不等式x2+bx+c>x+m 的解集.
解:∵直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2),
∴根据图象可知,不等式x2+bx+c>x+m 的解集为x<1或x>3;
故答案为:x<1或x>3.
点评:主要考查了二次函数与不等式组,解题的关键是根据图象找出直线y=x+m和抛物线y=x2+bx+c的交点,要具备读图的能力.
7.【解析】本题是一道估算题,先测估计出对称轴左侧图象与x轴交点的横坐标,再利用对称轴x=3,可以算出右侧交点横坐标.
解:依题意得二次函数y=ax2+bx+c的部分图象的对称轴为x=3,
而对称轴左侧图象与x轴交点与原点的距离,约为1.6,
∴x1=1.6;
又∵对称轴为x=3,
则=3,
∴x2=2×3﹣1.6=4.4.
点评:解答本题首先需要估计图象估计出一个解,再根据对称性计算出另一个解,估计值的精确程度,直接关系到计算的准确性,必须估计尽量准确.
8.【解析】二次函数y=(x﹣m)2+ ( http: / / www.21cnjy.com )b的顶点坐标为(m,b),由图象得,m=2,b=﹣2,可得二次函数的解析式为y=(x﹣2)2﹣2.再解一元二次方程即可.
解:由图象得,m=2,b=﹣2,
所以二次函数的解析式为y=(x﹣2)2﹣2.
关于x的一元二次方程(x﹣2)2﹣2=0
(x﹣2)2=2
解得:,.
故答案为:,.
点评:本题主要考查了抛物线与x轴的交点问题,本题的关键是得出二次函数的解析式为y=(x﹣2)2﹣2.
9.【解析】从图上可知,mx+n<ax2+bx+c,则有x>1或x<﹣;根据ax2+bx+c<0,可知﹣1<x<2;综上,不等式mx+n<ax2+bx+c<0的解集是1<x<2.
解:因为mx+n<ax2+bx+c<0,由图可知,1<x<2.
点评:此题将图形与不等式相结合,考查了同学们对不等式组的解集的理解和读图能力,有一定的难度,读图时要仔细.
三、解答题
10.【解析】根据函数与方程的关系,可得函数图象与x轴的交点的横坐标就是相应的方程的解.
解:方程x2﹣2x﹣1=0根是函数y=x2﹣2x﹣1与x轴交点的横坐标.
作出二次函数y=x2﹣2x﹣1的图象,如图所示,
由图象可知方程有两个根,一个在﹣1和0之间,另一个在2和3之间.
先求﹣1和0之间的根,
当x=﹣0.4时,y=﹣0.04;当x=﹣0.5时,y=0.25;
因此,x=﹣0.4(或x=﹣0.5)是方程的一个近似根,
同理,x=2.4(或x=2.5)是方程的另一个近似根.
( http: / / www.21cnjy.com )
点评:本题考查了图象法求一元二次方程的近似值,解答此题的关键是求出对称轴,然后由图象解答,锻炼了学生数形结合的思想方法.
11.【解析】(1)用配方法解答一元二次方程;
(2)二次函数方程为y=ax2 ( http: / / www.21cnjy.com )+bx+c与x轴交点的横坐标就是方程x2﹣x﹣1=0的解,所以,只要求出方程x2﹣x﹣1=0的根,就可以求出二次函数方程为y=ax2+bx+c与x轴交点;
(3)由(1)(2)解得x1、x2,再根据题意画出图象.
解:(1)由原方程,得:
,即;
解得x1= ,x2=.
(2)设二次函数方程为y=ax2+bx+c(a,b,c均为实数,且a≠0).
由图象得知,该函数过点(0,﹣1),所以该点满足方程y=ax2+bx+c,
∴把(0,﹣1)代入方程y=ax2+bx+c,得c=﹣1,①
二次函数方程为y=ax2+bx+c与x轴交点的横坐标就是方程x2﹣x﹣1=0的解;
∴x1 x2==﹣1,即c=﹣a;②
x1+x2==1;③
由①②③,得:
;
∴二次函数方程为y=x2﹣x﹣1.
(3)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
点评:本题考查的是二次函数与一元二次方程,在解答过程中,注意二次函数与一元二次方程之间的联系,并从中择取有用信息解题.
12.【解析】(1)联立两函数解析式求解即可;
(2)根据函数图象写出抛物线直线上方部分的x的取值范围即可.
解:(1)联立,
解得: 或,
所以A、B两点的坐标分别是(﹣1,0),(0,2);
(2)由图可知,﹣<x<0时,y1>y2.
点评:本题考查二次函数与不等式,主要利用了联立两函数解析式求交点坐标的方法,利用函数图象求不等式的解集,利用数形结合的思想求解是更简便.
13.【解析】画出二次函数y=x2+7x+9的图象,则一元二次方程x2+7x+9=1的根为图象中y=1时x的值.
解:一元二次方程x2+7x+9=1的根是二次函数y=x2+7x+9图象中y=1时,所对应的x的值;
当y=1时,x2+7x+9=1,
∴作出二次函数y=x2+7x+9的图象如图,由图中可以看出,当y=1时,x≈﹣5.6或﹣1.4,
∴一元二次方程x2+7x+9=1的根为x1≈﹣5.6,x2≈﹣1.4.
( http: / / www.21cnjy.com )
点评:考查二次函数图象与一元二次方程近似跟的关系;关键是得到一元二次方程的图象;难点是判断出一元二次方程的根在图象中的位置.
同课章节目录
