【多媒体导学案】人教版数学九年级上册第22章第3课时二次函数y=ax2+k的图象和性质(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第22章第3课时二次函数y=ax2+k的图象和性质(教师版) |
|
|
| 格式 | zip | ||
| 文件大小 | 879.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-15 00:00:00 | ||
图片预览




文档简介
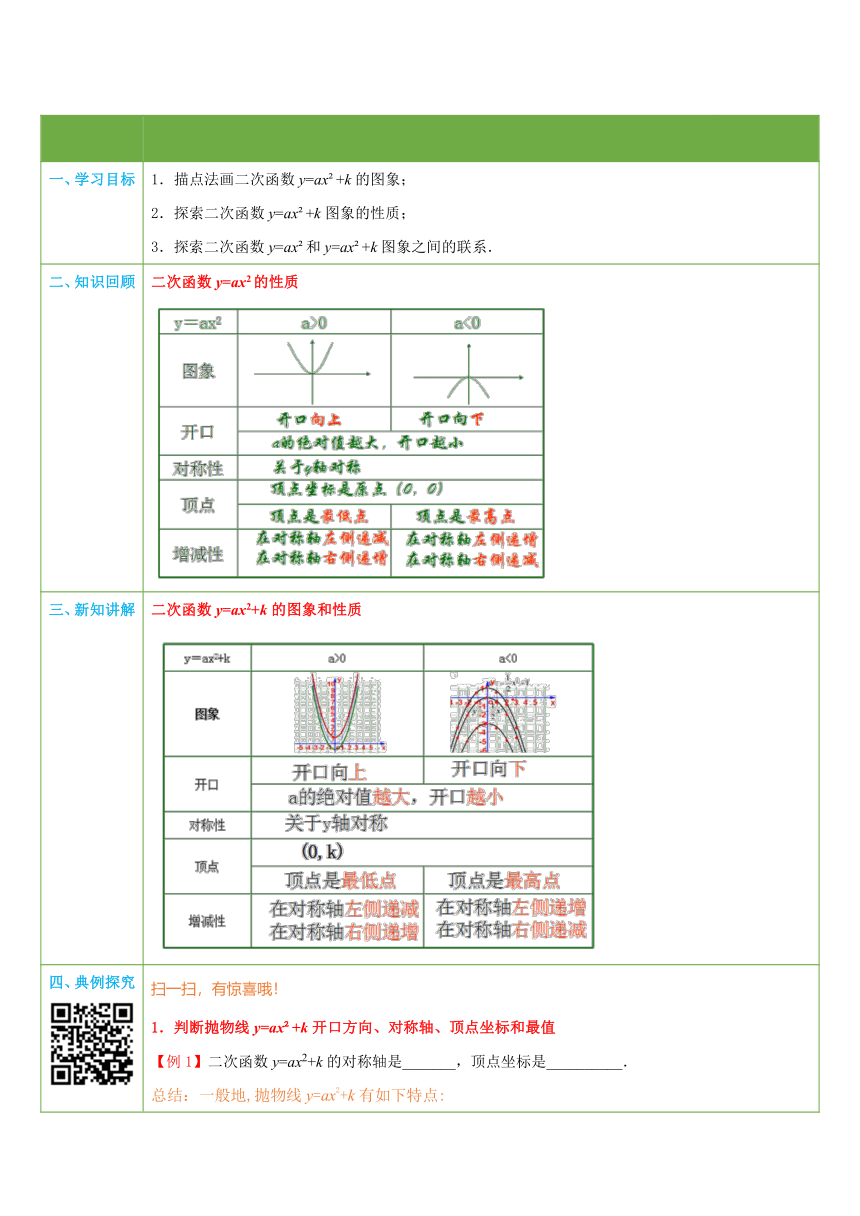
一、学习目标 1.描点法画二次函数y=ax +k的图象;2.探索二次函数y=ax +k图象的性质;3.探索二次函数y=ax 和y=ax +k图象之间的联系.
二、知识回顾 二次函数y=ax2的性质 ( http: / / www.21cnjy.com )
三、新知讲解 二次函数y=ax2+k的图象和性质 ( http: / / www.21cnjy.com )
四、典例探究 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) 扫一扫,有惊喜哦!1.判断抛物线y=ax +k开口方向、对称轴、顶点坐标和最值【例1】二次函数y=ax2+k的对称轴是_______,顶点坐标是__________.总结:一般地,抛物线y=ax2+k有如下特点:(1)当a>0时,开口向上;当a<0时,开口向下;(2)对称轴是y轴;(3)顶点是(0,k).练1抛物线y=﹣2x2+3,对称轴是________,开口向_______.2.抛物线y=ax 和y=ax +k之间的平移规律【例2】(2015 杭州模拟)二次函数y=﹣3x2+1的图象是将()A.抛物线y=﹣3x2向左平移3个单位得到B.抛物线y=﹣3x2向左平移1个单位得到C.抛物线y=3x2向上平移1个单位得到D.抛物线y=﹣3x2向上平移1个单位得到总结:抛物线y=ax2+k可以由抛物线y ( http: / / www.21cnjy.com )=ax2向上或向下平移|k|得到.当k>0时,抛物线y=ax2向上平移|k|个单位得到抛物线y=ax2+k;当k<0时, 抛物线y=ax2向下平移|k|个单位得到抛物线y=ax2+k .练2在平面直角坐标系中,将抛物线y=2x2向下平移2个单位,那么所得抛物线的表达式为()A.y=2x2﹣2 B.y=2x2+2 C.y=2(x﹣2)2 D.y=2(x+2)23.根据y=ax +k图象上两点的坐标求a,k【例3】二次函数y=ax2+k图象与坐标轴交于点(0,2)和(1,0),求该函数的关系式.总结:已知二次函数y=ax2+k图象上两点 ( http: / / www.21cnjy.com )坐标即可求得其解析式.步骤是:把两点坐标代入y=ax2+k,得到关于a、k的方程组,然后解方程组求得a,k,最后把a,k的值代回原解析式即可.练3已知抛物线y=ax2+k经过点(1,-1),且顶点坐标是(0,-2)求a,k的值.
五、课后小测 一、选择题1.(2015 金山区一模)抛物线y=2x2+1的顶点坐标是( )A.(2,1) B.(0,1) C.(1,0) D.(1,2)2.(2015 邛崃市模拟)将y=x2向上平移2个单位后所得的抛物线的解析式为( )A.y=x2+2 B.y=x2﹣2 C.y=(x+2)2 D.y=(x﹣2)23.(2014 余姚市模拟)将抛物线y=x2平移得到抛物线y=x2+3,则下列平移过程正确的是( )A.向上平移3个单位 B.向下平移3个单位C.向左平移3个单位 D.向右平移3个单位4.(2014 河池)已知点(x1,y1),(x2,y2)均在抛物线y=x2﹣1上,下列说法中正确的是( )A.若y1=y2,则x1=x2 B.若x1=﹣x2,则y1=﹣y2C.若0<x1<x2,则y1>y2 D.若x1<x2<0,则y1>y25.(2014秋 崂山区校级期末)二次函数 ( http: / / www.21cnjy.com )y=﹣2x2+1的图象上有两点P1(x1,y1),P2(x2,y2),当0<x1<x2时,则y1,y2的大小关系是( )A.y1>y2 B.y1<y2<0 C.y1>y2>0 D.y1<y26.(2015 山西模拟)已知二次函数y1=﹣3x2,,,它们的图象开口由小到大的顺序是( )A.y1<y2<y3 B.y3<y2<y1 C.y1<y3<y2 D.y2<y3<y1二、填空题7.(2009 普陀区一模)二次函数y=2x2+3图象的顶点坐标是__________.8.(2015 松江区二模)将抛物线y=2x2﹣1向上平移4个单位后,所得抛物线的解析式是_______.9.(2014 杭州模拟) ( http: / / www.21cnjy.com )已知抛物线y=ax2+c(a>0)过A(﹣3,y1)、B(﹣7,y2)、C(4,y3)三点,把y1、y2、y3从小到大的顺序排列为_________________.10.(2015 成都校级模拟)若抛物 ( http: / / www.21cnjy.com )线y=ax2+c与y=2x2的形状相同,开口方向相反,且其顶点坐标是(0,﹣2),则该抛物线的函数表达式是______________.三、解答题11.在同一直角坐标系中画出二次函数y=x2+1与二次函数y=﹣x2﹣1的图形.(1)从抛物线的开口方向、形状、对称轴、顶点等方面说出两个函数图象的相同点与不同点;(2)说出两个函数图象的性质的相同点与不同点.
典例探究答案:
【例1】【解析】利用公式法即可求出二次函数y=ax2+k的对称轴和顶点坐标.
解:∵y=ax2+k,
∴对称轴x=﹣=0,顶点横纵坐标分别是:x=0,y=k,
故答案为:x=0,(0,k).
点评:本题考查了二次函数的性质,牢记其顶点坐标公式是解决二次函数的有关知识的基础.
练1.【解析】由于a=﹣2<0,图象开口向下;由于b=0,对称轴x=﹣=0.
解:因为a=﹣2<0,所以开口向下;
根据对称轴公式x=﹣,可得对称轴x=0.
点评:主要考查了二次函数的性质和求抛物线的顶点坐标、对称轴的方法.
【例2】【解析】根据平移规律判断各选项即可.
解:二次函数y=﹣3x2+1的图象是将抛物线y=﹣3x2向上平移1个单位得到的.
故选D.
点评:主要考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.
练2.【解析】由于原抛物线的顶点坐 ( http: / / www.21cnjy.com )标为(0,0),则将抛物线y=2x2向下平移2个单位所得抛物线的顶点坐标为(0,﹣2),然后根据顶点式写出平移后抛物线的解析式.
解:抛物线y=2x2向下平移2个单位,所得抛物线的表达式为y=2x2﹣2.
故选A.
点评:本题考查了二次函数与几何变换 ( http: / / www.21cnjy.com ):由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.
【例3】【解析】把点(0,2)和(1,0)直接代入y=ax2+k得到关于a、k的方程组,然后解方程组即可.
解:根据题意得,解得,
所以二次函数解析式为y=﹣2x2+2.
点评:本题考查了待定系数法求二次函数的解析式 ( http: / / www.21cnjy.com ):在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.
练3.【解析】根据顶点坐标确定出k值,再将另一点坐标代入解析式求得a的值.
解:∵抛物线y=ax2+k的顶点坐标为(0,-2),∴k=﹣2,抛物线解析式为y=ax2-2.
把(1,-1)代入抛物线y=ax2-2中,得
a-2=-1,解得a=1.
综上,得a=1,k=-2
点评:本题考查了点与函数的关系,解题的关键是代入求值.
课后小测答案:
一、选择题
1.【解析】根据二次函数的顶点式可求得其顶点坐标.
解:
∵y=2x2+1=2(x﹣0)2+1,
∴抛物线的顶点坐标为(0,1),
故选B.
点评:本题主要考查抛物线的顶点坐标,掌握顶点式方程y=a(x﹣h)2+k的顶点坐标为(h,k)是解题的关键.
2.【解析】先得到抛物线y ( http: / / www.21cnjy.com )=x2的顶点坐标为(0,0),由于点(0,0)向上平移2个单位得到的点的坐标为(0,2),则利用顶点式可得到平移后的抛物线的解析式为y=x2+2.
解:抛物线y=x2的顶点 ( http: / / www.21cnjy.com )坐标为(0,0),把点(0,0)向上平移2个单位得到的点的坐标为(0,2),所以平移后的抛物线的解析式为y=x2+2.
故选:A.
点评:本题考查了二次函数图象与几何变换 ( http: / / www.21cnjy.com ):由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.
3.【解析】根据“上加下减”的原则直接进行解答即可.
解:由“上加下减”的原则可知,将抛物线y=x2向上平移得到抛物线y=x2+3.
故选:A.
点评:本题考查的是二次函数的图象与几何变换,熟知“上加下减”的原则是解答此题的关键.
4.【解析】由于抛物线y=x2﹣1的图 ( http: / / www.21cnjy.com )象关于y轴对称,开口向上,分别判断如下:若y1=y2,则x1=﹣x2;若x1=﹣x2,则y1=y2;若0<x1<x2,则在对称轴的右侧,y随x的增大而增大,则y1<y2;若x1<x2<0,则y1>y2.
解:A、若y1=y2,则x1=﹣x2;
B、若x1=﹣x2,则y1=y2;
C、若0<x1<x2,则在对称轴的右侧,y随x的增大而增大,则y1<y2;
D、正确.
故选D.
( http: / / www.21cnjy.com )
点评:本题的关键是(1)找到二次函数的对称轴;(2)掌握二次函数图象的性质.
5.【解析】根据二次函数图象上点的 ( http: / / www.21cnjy.com )坐标特征得到y1=﹣2x12+1,y2=﹣2x22+1,然后根据0<x1<x2即可得到y1,y2的大小关系.
解:∵二次函数y=﹣2x2+1的图象上有两点P1(x1,y1),P2(x2,y2),
∴y1=﹣2x12+1,y2=﹣2x22+1,
∵0<x1<x2,
∴y1>y2.
故选A.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.注意代数式的大小比较.
6.【解析】抛物线的开口大小由二次项系数的绝对值大小确定,绝对值越大,开口越小.
解:∵|﹣3|>||>|﹣|,二次项系数的绝对值越大,抛物线开口越小,
∴y1<y3<y2,故选C.
点评:考查二次项系数的绝对值越大,函数值随x值的增大变化越大,抛物线开口越小.
二、填空题
7.【解析】已知二次函数y=2x2+3为抛物线的顶点式,根据顶点式的坐标特点直接写出顶点坐标.
解:∵y=2x2+3=2(x﹣0)2+3,
∴顶点坐标为(0,3).
点评:对照顶点式的形式变形,可求顶点坐标.
8.【解析】直接利用二次函数图象平移规律得出即可.
解:∵将抛物线y=2x2﹣1向上平移4个单位,
∴平移后解析式为:y=2x2+3.
故答案为:y=2x2+3.
点评:此题主要考查了二次函数图象与几何变换,正确记忆平移规律是解题关键.
9.【解析】先求出抛物线的对称轴为y轴和开口方向,再根据二次函数的对称性解答.
解:抛物线y=ax2+c的对称轴为y轴,
∵a>0,
∴抛物线开口向上,
∵点A、B、C到对称轴的距离分别为3、7、4,
∴y1、y2、y3从小到大的顺序排列为y1<y3<y2.
故答案为:y1<y3<y2.
点评:本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的对称性和增减性以及开口方向,利用性质求解更加简便.
10.【解析】根据两抛物线形状相同,开口方向相反,求出a的值,再将顶点坐标代入求出c的值,即可确定出解析式.
解:根据题意得:y=﹣2x2+c,
把(0,﹣2)代入得:c=﹣2,
则该抛物线解析式为y=﹣2x2﹣2.
故答案为:y=﹣2x2﹣2.
点评:此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.
三、解答题
11.【解析】根据二次函数图象,可得二次函数的性质.
解:如图:
( http: / / www.21cnjy.com ),
(1)y=x2+1与y=﹣x2﹣1的相同点是:形状都是抛物线,对称轴都是y轴,
y=x2+1与y=﹣x2﹣1的不同点是:y=x2+1开口向上,顶点坐标是(0,1),y=﹣x2﹣1开口向下,顶点坐标是(0,﹣1);
(2)性质的相同点:开口程度相同,不同点:y=x2+1 当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大;
y=﹣x2﹣1当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.
点评:本题考查了二次函数的图象,利用了二 ( http: / / www.21cnjy.com )次函数图象与性质,a>0图象开口向上,对称轴左侧,y随x的增大而减小,对称轴右侧,y随x的增大而增大;a<0图象开口向下,对称轴左侧,y随x的增大而增大,对称轴右侧,y随x的增大而减小.
附件1:律师事务所反盗版维权声明
( http: / / www.21cnjy.com )
附件2:独家资源交换签约学校名录(放大查看)
学校名录参见:http://21世纪教育网/wxt/list. aspx ClassID=3060
二、知识回顾 二次函数y=ax2的性质 ( http: / / www.21cnjy.com )
三、新知讲解 二次函数y=ax2+k的图象和性质 ( http: / / www.21cnjy.com )
四、典例探究 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) 扫一扫,有惊喜哦!1.判断抛物线y=ax +k开口方向、对称轴、顶点坐标和最值【例1】二次函数y=ax2+k的对称轴是_______,顶点坐标是__________.总结:一般地,抛物线y=ax2+k有如下特点:(1)当a>0时,开口向上;当a<0时,开口向下;(2)对称轴是y轴;(3)顶点是(0,k).练1抛物线y=﹣2x2+3,对称轴是________,开口向_______.2.抛物线y=ax 和y=ax +k之间的平移规律【例2】(2015 杭州模拟)二次函数y=﹣3x2+1的图象是将()A.抛物线y=﹣3x2向左平移3个单位得到B.抛物线y=﹣3x2向左平移1个单位得到C.抛物线y=3x2向上平移1个单位得到D.抛物线y=﹣3x2向上平移1个单位得到总结:抛物线y=ax2+k可以由抛物线y ( http: / / www.21cnjy.com )=ax2向上或向下平移|k|得到.当k>0时,抛物线y=ax2向上平移|k|个单位得到抛物线y=ax2+k;当k<0时, 抛物线y=ax2向下平移|k|个单位得到抛物线y=ax2+k .练2在平面直角坐标系中,将抛物线y=2x2向下平移2个单位,那么所得抛物线的表达式为()A.y=2x2﹣2 B.y=2x2+2 C.y=2(x﹣2)2 D.y=2(x+2)23.根据y=ax +k图象上两点的坐标求a,k【例3】二次函数y=ax2+k图象与坐标轴交于点(0,2)和(1,0),求该函数的关系式.总结:已知二次函数y=ax2+k图象上两点 ( http: / / www.21cnjy.com )坐标即可求得其解析式.步骤是:把两点坐标代入y=ax2+k,得到关于a、k的方程组,然后解方程组求得a,k,最后把a,k的值代回原解析式即可.练3已知抛物线y=ax2+k经过点(1,-1),且顶点坐标是(0,-2)求a,k的值.
五、课后小测 一、选择题1.(2015 金山区一模)抛物线y=2x2+1的顶点坐标是( )A.(2,1) B.(0,1) C.(1,0) D.(1,2)2.(2015 邛崃市模拟)将y=x2向上平移2个单位后所得的抛物线的解析式为( )A.y=x2+2 B.y=x2﹣2 C.y=(x+2)2 D.y=(x﹣2)23.(2014 余姚市模拟)将抛物线y=x2平移得到抛物线y=x2+3,则下列平移过程正确的是( )A.向上平移3个单位 B.向下平移3个单位C.向左平移3个单位 D.向右平移3个单位4.(2014 河池)已知点(x1,y1),(x2,y2)均在抛物线y=x2﹣1上,下列说法中正确的是( )A.若y1=y2,则x1=x2 B.若x1=﹣x2,则y1=﹣y2C.若0<x1<x2,则y1>y2 D.若x1<x2<0,则y1>y25.(2014秋 崂山区校级期末)二次函数 ( http: / / www.21cnjy.com )y=﹣2x2+1的图象上有两点P1(x1,y1),P2(x2,y2),当0<x1<x2时,则y1,y2的大小关系是( )A.y1>y2 B.y1<y2<0 C.y1>y2>0 D.y1<y26.(2015 山西模拟)已知二次函数y1=﹣3x2,,,它们的图象开口由小到大的顺序是( )A.y1<y2<y3 B.y3<y2<y1 C.y1<y3<y2 D.y2<y3<y1二、填空题7.(2009 普陀区一模)二次函数y=2x2+3图象的顶点坐标是__________.8.(2015 松江区二模)将抛物线y=2x2﹣1向上平移4个单位后,所得抛物线的解析式是_______.9.(2014 杭州模拟) ( http: / / www.21cnjy.com )已知抛物线y=ax2+c(a>0)过A(﹣3,y1)、B(﹣7,y2)、C(4,y3)三点,把y1、y2、y3从小到大的顺序排列为_________________.10.(2015 成都校级模拟)若抛物 ( http: / / www.21cnjy.com )线y=ax2+c与y=2x2的形状相同,开口方向相反,且其顶点坐标是(0,﹣2),则该抛物线的函数表达式是______________.三、解答题11.在同一直角坐标系中画出二次函数y=x2+1与二次函数y=﹣x2﹣1的图形.(1)从抛物线的开口方向、形状、对称轴、顶点等方面说出两个函数图象的相同点与不同点;(2)说出两个函数图象的性质的相同点与不同点.
典例探究答案:
【例1】【解析】利用公式法即可求出二次函数y=ax2+k的对称轴和顶点坐标.
解:∵y=ax2+k,
∴对称轴x=﹣=0,顶点横纵坐标分别是:x=0,y=k,
故答案为:x=0,(0,k).
点评:本题考查了二次函数的性质,牢记其顶点坐标公式是解决二次函数的有关知识的基础.
练1.【解析】由于a=﹣2<0,图象开口向下;由于b=0,对称轴x=﹣=0.
解:因为a=﹣2<0,所以开口向下;
根据对称轴公式x=﹣,可得对称轴x=0.
点评:主要考查了二次函数的性质和求抛物线的顶点坐标、对称轴的方法.
【例2】【解析】根据平移规律判断各选项即可.
解:二次函数y=﹣3x2+1的图象是将抛物线y=﹣3x2向上平移1个单位得到的.
故选D.
点评:主要考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.
练2.【解析】由于原抛物线的顶点坐 ( http: / / www.21cnjy.com )标为(0,0),则将抛物线y=2x2向下平移2个单位所得抛物线的顶点坐标为(0,﹣2),然后根据顶点式写出平移后抛物线的解析式.
解:抛物线y=2x2向下平移2个单位,所得抛物线的表达式为y=2x2﹣2.
故选A.
点评:本题考查了二次函数与几何变换 ( http: / / www.21cnjy.com ):由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.
【例3】【解析】把点(0,2)和(1,0)直接代入y=ax2+k得到关于a、k的方程组,然后解方程组即可.
解:根据题意得,解得,
所以二次函数解析式为y=﹣2x2+2.
点评:本题考查了待定系数法求二次函数的解析式 ( http: / / www.21cnjy.com ):在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.
练3.【解析】根据顶点坐标确定出k值,再将另一点坐标代入解析式求得a的值.
解:∵抛物线y=ax2+k的顶点坐标为(0,-2),∴k=﹣2,抛物线解析式为y=ax2-2.
把(1,-1)代入抛物线y=ax2-2中,得
a-2=-1,解得a=1.
综上,得a=1,k=-2
点评:本题考查了点与函数的关系,解题的关键是代入求值.
课后小测答案:
一、选择题
1.【解析】根据二次函数的顶点式可求得其顶点坐标.
解:
∵y=2x2+1=2(x﹣0)2+1,
∴抛物线的顶点坐标为(0,1),
故选B.
点评:本题主要考查抛物线的顶点坐标,掌握顶点式方程y=a(x﹣h)2+k的顶点坐标为(h,k)是解题的关键.
2.【解析】先得到抛物线y ( http: / / www.21cnjy.com )=x2的顶点坐标为(0,0),由于点(0,0)向上平移2个单位得到的点的坐标为(0,2),则利用顶点式可得到平移后的抛物线的解析式为y=x2+2.
解:抛物线y=x2的顶点 ( http: / / www.21cnjy.com )坐标为(0,0),把点(0,0)向上平移2个单位得到的点的坐标为(0,2),所以平移后的抛物线的解析式为y=x2+2.
故选:A.
点评:本题考查了二次函数图象与几何变换 ( http: / / www.21cnjy.com ):由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.
3.【解析】根据“上加下减”的原则直接进行解答即可.
解:由“上加下减”的原则可知,将抛物线y=x2向上平移得到抛物线y=x2+3.
故选:A.
点评:本题考查的是二次函数的图象与几何变换,熟知“上加下减”的原则是解答此题的关键.
4.【解析】由于抛物线y=x2﹣1的图 ( http: / / www.21cnjy.com )象关于y轴对称,开口向上,分别判断如下:若y1=y2,则x1=﹣x2;若x1=﹣x2,则y1=y2;若0<x1<x2,则在对称轴的右侧,y随x的增大而增大,则y1<y2;若x1<x2<0,则y1>y2.
解:A、若y1=y2,则x1=﹣x2;
B、若x1=﹣x2,则y1=y2;
C、若0<x1<x2,则在对称轴的右侧,y随x的增大而增大,则y1<y2;
D、正确.
故选D.
( http: / / www.21cnjy.com )
点评:本题的关键是(1)找到二次函数的对称轴;(2)掌握二次函数图象的性质.
5.【解析】根据二次函数图象上点的 ( http: / / www.21cnjy.com )坐标特征得到y1=﹣2x12+1,y2=﹣2x22+1,然后根据0<x1<x2即可得到y1,y2的大小关系.
解:∵二次函数y=﹣2x2+1的图象上有两点P1(x1,y1),P2(x2,y2),
∴y1=﹣2x12+1,y2=﹣2x22+1,
∵0<x1<x2,
∴y1>y2.
故选A.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.注意代数式的大小比较.
6.【解析】抛物线的开口大小由二次项系数的绝对值大小确定,绝对值越大,开口越小.
解:∵|﹣3|>||>|﹣|,二次项系数的绝对值越大,抛物线开口越小,
∴y1<y3<y2,故选C.
点评:考查二次项系数的绝对值越大,函数值随x值的增大变化越大,抛物线开口越小.
二、填空题
7.【解析】已知二次函数y=2x2+3为抛物线的顶点式,根据顶点式的坐标特点直接写出顶点坐标.
解:∵y=2x2+3=2(x﹣0)2+3,
∴顶点坐标为(0,3).
点评:对照顶点式的形式变形,可求顶点坐标.
8.【解析】直接利用二次函数图象平移规律得出即可.
解:∵将抛物线y=2x2﹣1向上平移4个单位,
∴平移后解析式为:y=2x2+3.
故答案为:y=2x2+3.
点评:此题主要考查了二次函数图象与几何变换,正确记忆平移规律是解题关键.
9.【解析】先求出抛物线的对称轴为y轴和开口方向,再根据二次函数的对称性解答.
解:抛物线y=ax2+c的对称轴为y轴,
∵a>0,
∴抛物线开口向上,
∵点A、B、C到对称轴的距离分别为3、7、4,
∴y1、y2、y3从小到大的顺序排列为y1<y3<y2.
故答案为:y1<y3<y2.
点评:本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的对称性和增减性以及开口方向,利用性质求解更加简便.
10.【解析】根据两抛物线形状相同,开口方向相反,求出a的值,再将顶点坐标代入求出c的值,即可确定出解析式.
解:根据题意得:y=﹣2x2+c,
把(0,﹣2)代入得:c=﹣2,
则该抛物线解析式为y=﹣2x2﹣2.
故答案为:y=﹣2x2﹣2.
点评:此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.
三、解答题
11.【解析】根据二次函数图象,可得二次函数的性质.
解:如图:
( http: / / www.21cnjy.com ),
(1)y=x2+1与y=﹣x2﹣1的相同点是:形状都是抛物线,对称轴都是y轴,
y=x2+1与y=﹣x2﹣1的不同点是:y=x2+1开口向上,顶点坐标是(0,1),y=﹣x2﹣1开口向下,顶点坐标是(0,﹣1);
(2)性质的相同点:开口程度相同,不同点:y=x2+1 当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大;
y=﹣x2﹣1当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.
点评:本题考查了二次函数的图象,利用了二 ( http: / / www.21cnjy.com )次函数图象与性质,a>0图象开口向上,对称轴左侧,y随x的增大而减小,对称轴右侧,y随x的增大而增大;a<0图象开口向下,对称轴左侧,y随x的增大而增大,对称轴右侧,y随x的增大而减小.
附件1:律师事务所反盗版维权声明
( http: / / www.21cnjy.com )
附件2:独家资源交换签约学校名录(放大查看)
学校名录参见:http://21世纪教育网/wxt/list. aspx ClassID=3060
同课章节目录
