【多媒体导学案】人教版数学九年级上册第22章第4课时二次函数y=a(x-h)2的图象和性质(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第22章第4课时二次函数y=a(x-h)2的图象和性质(教师版) |
|
|
| 格式 | doc | ||
| 文件大小 | 309.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-15 00:00:00 | ||
图片预览




文档简介
二次函数y=a(x-h)2的图象和性质(教师版)
一、学习目标 会用描点法画出二次函数y=a(x-h)2的图象,能通过图象和关系式认识二次函数的性质;通过独立思考、小组合作、动手操作,掌握二次函数y=a(x-h)2的性质,并会灵活应用.
二、知识回顾 1.二次函数y=ax2,y=ax2+k图象是什么?抛物线.2.二次函数y=ax2+k的图象是由二次函数y=ax2的图象怎样运动得到?若k>0,抛物线y=ax2向上平移k个单位得抛物线y=ax2+k;若k<0,抛物线y=ax2向下平移个单位得抛物线y=ax2+k.3.二次函数y=ax2,y=ax2+k的性质有哪些?请填写下表.函数开口方向对称轴顶点坐标y的最值y=ax2a>0向上y轴(0,0)最小值是0a<0向下y轴(0,0)最大值是0y=ax2+ka>0向上y轴(0,k)最小值是ka<0向下y轴(0,k)最大值是k
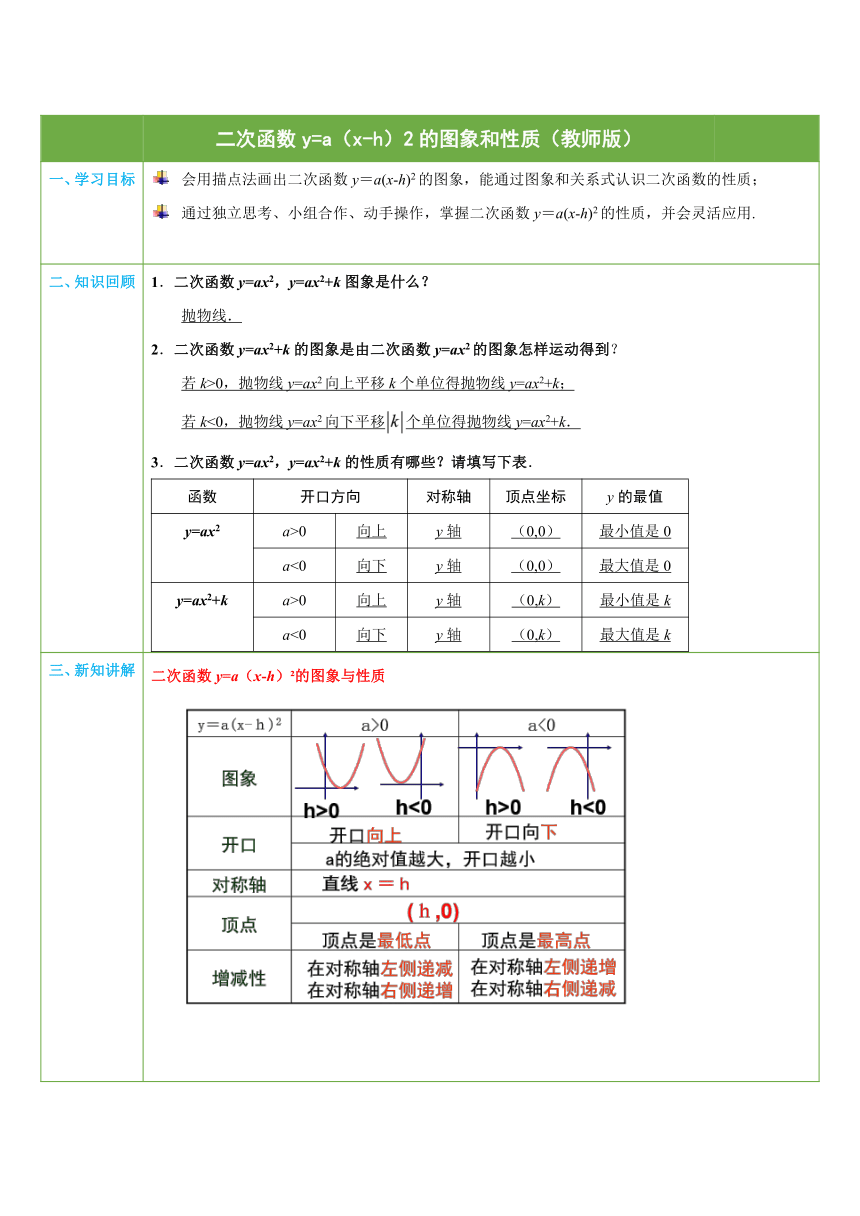
三、新知讲解 二次函数y=a(x-h) 的图象与性质 ( http: / / www.21cnjy.com )
四、典例探究 扫一扫,有惊喜哦!1.考查抛物线y=a(x-h) 开口方向、对称轴和顶点坐标【例1】抛物线y=﹣3(x﹣1)2的开口向 ,对称轴是 ,顶点坐标是 .总结:函数y=ax2与y=a(x-h) 的图象开口方向相同,对称轴和顶点坐标不同.函数y=a(x-h) 的对称轴是直线x=h,顶点坐标是(h,0).练1.抛物线y=(x﹣1)2的开口向 ,顶点是 ,对称轴是 .2.考查二次函数y=a(x-h) 的增减性【例2】(2012 石鼓区校级一模)已知二次函数y=(x﹣2)2,当x 时,y随x增大而减小.总结:1.当a>0时,在对称轴(x=h)的左侧 ( http: / / www.21cnjy.com ),y随着x的增大而减小;在对称轴(x=h)右侧,y随着x的增大而增大;当x=h时函数y的值最小(是0).2.当a<0时,在对称轴(x=h)的左侧, ( http: / / www.21cnjy.com )y随着x的增大而增大;在对称轴(x=h)的右侧,y随着x增大而减小;当x=h时,函数y的值最大(是0).练2.二次函数y=﹣(x+3)2,当x 时, y随x的增大而增大,当x 时,随x的增大而减小.3.考查抛物线y=a(x-h) 和y=ax 之间的平移规律【例3】将抛物线y=x2向右平移2个单位,得到新抛物线的表达式是 .总结:1.抛物线的平移不改变二次项的系数,主要是移动顶点位置.2.抛物线y=ax 向右平移h(h>0)个 ( http: / / www.21cnjy.com )单位得到抛物线y=a(x-h) , y=ax 向左平移h(h>0)个单位得到抛物线y=a(x+h) ,简称“左加右减”.练3.(2013 崇明县一模)将抛物线y=(x+1)2向右平移2个单位,得到新抛物线的顶点坐标是 .
五、课后小测 一、选择题1.(2015 嘉定区一模)对于抛物线y=(x﹣2)2,下列说法正确的是( )A.顶点坐标是(2,0) B.顶点坐标是(0,2)C.顶点坐标是(﹣2,0) D.顶点坐标是(0,﹣2)2.(2013秋 泗洪县期末)抛物线y=(x+1)2的顶点坐标是( )A.(﹣1,0) B.(1,0) C.(0,1) D.(0,﹣1)二、填空题3.抛物线y=﹣(x+1) ( http: / / www.21cnjy.com )2的开口 ,对称轴是 ,顶点坐标是 ,它可以看作是由抛物线y=﹣x2向 平移 个单位长度得到的.4.(2014秋 荔湾区期末)将抛物线y=﹣2x2向右平移2个单位,得到的抛物线的解析式是 .5. 将抛物线y=-3x2向左平移2个单位,得到新抛物线的顶点坐标是 .6.(2013秋 沈丘县校级月考)二次函数y=a(x﹣h)2的对称轴是 ,顶点坐标是 .7.已知抛物线y=a(x﹣h)2的最高点的横坐标为2,当x 时,y随x的增大而减小.三、解答题8.(2014秋 丹江口市校级月考)已知二次函数y=﹣(x﹣2)2.(1)画出函数图象,确定抛物线的开口方向、顶点坐标和对称轴;(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小? ( http: / / www.21cnjy.com )9.已知抛物线y=a(x﹣h)2经过点(﹣3,2)、(﹣1,0),求该抛物线的解析式.10.(2012 淄博)已知:抛物线.(1)写出抛物线的对称轴;(2)完成下表;x…﹣7﹣313…y…﹣9﹣1…(3)在下面的坐标系中描点画出抛物线的图象. ( http: / / www.21cnjy.com )11.已知抛物线y=a(x﹣h)2的对称轴为直线x=﹣2,且抛物线与y轴交于点(0,2),求a,h的值.12.已知,函数y=x2,y=(x+3)2和y=(x﹣3)2(1)在同一直角坐标系中画出它们的图象;(2)分别说出各个函数图象的开口方向,对称轴和顶点坐标.13.(2010秋 安庆期末)已知抛物线y=a(x﹣h)2向右平移3个单位后,得到抛物线y=2(x+1)2,求a、h的值.
典例探究答案
【例1】
分析:已知抛物线解析式为顶点式,可根据顶点式求抛物线的开口方向,对称轴及顶点坐标.
解答:解:由y=﹣3(x﹣1)2可知,二次项系数为﹣3<0,
∴抛物线开口向下,对称轴为直线x=1,
顶点坐标为(1,0).
故本题答案为:向下,x=1,(1,0).
点评:本题考查了二次函数解析式的顶点式与其性质的联系,根据二次项系数的符号确定开口方向,根据顶点式确定顶点坐标及对称轴.
练1.
分析:根据二次函数的性质分别填空即可.
解答:解:抛物线y=(x﹣1)2的开口向下,
顶点是(1,0),
对称轴是直线x=1.
故答案为:下,(1,0),直线x=1.
点评:本题考查了二次函数的性质,主要是利用顶点式解析式求解顶点坐标和对称轴的方法,需熟记.
【例2】
分析:根据函数解析式可知,开口方向向上,在对称轴的左侧y随x的增大而减小,在对称轴的右侧,y随x的增大而增大.
解答:解:∵函数的对称轴为x=2,
又∵二次函数开口向上,
∴在对称轴的左侧y随x的增大而减小,
∴x<2时,y随x增大而减小.
故答案为x<2.
点评:本题考查了二次函数的性质,能根据解析式推知函数图象是解题的关键,另外要能准确判断出函数的对称轴.
练2.
分析:利用二次函数的性质求解即可.
解答:解:∵函数y=﹣(x+3)2的对称轴为x=﹣3,且开口向下,
∴当x<﹣3时,函数y=﹣(x+3)2y随x的增大而增大,当x>﹣3时,随x的增大而减小.
故答案为:<﹣3,>﹣3.
点评:本题主要考查了二次函数的性质,解题的关键是熟记二次函数的性质.
【例3】
分析:可根据二次函数图象左加右减,上加下减的平移规律进行解答.
解答:解:二次函数y=x2的图象向右平移2个单位,
得:y=(x﹣2)2,
故答案为:y=(x﹣2)2.
点评:主要考查的是函数图象的平移,用平移规律“左加右减,上加下减”直接代入函数解析式求得平移后的函数解析式.
练3.
分析:先根据y=(x+1)2得到顶点(-1,0),然后把顶点(-1,0)向右平移2个单位即可得到平移后抛物线的顶点坐标.
解答:∵y=(x+1)2的顶点坐标为(﹣1,0),
∴抛物线y=(x+1)2向右平移2个单位后所得抛物线的顶点坐标为(1,0).
故答案为(1,0).
点评:本题考查了二次函数的图象与几何变换:先找到二次函数y=ax2的顶点,然后把抛物线的平移问题转化为顶点的平移问题.
课后小测答案:
一、选择题
1.解:抛物线y=(x﹣2)2的顶点坐标为(2,0),
故选A.
2.解:由抛物线的顶点坐标可知,抛物线y=(x+1)2的顶点坐标是(﹣1,0).
故选A.
二、填空题
3.解:抛物线y=﹣(x+1)2的开口 ( http: / / www.21cnjy.com )向下,对称轴是直线x=﹣1,顶点坐标是(﹣1,0),它可以看作是由抛物线y=﹣x2向左平移1个单位长度得到的.
故答案为:向下,直线x=﹣1,(﹣1,0),左,1.
4.解:抛物线y=﹣2x2向右平移2个单位后的函数抛物线的解析式为:y=﹣2(x﹣2)2.
故答案是:y=﹣2(x﹣2)2.
5.解:∵y=-3x2的顶点坐标为(0,0),
∴抛物线y=-3x2向左平移2个单位后所得抛物线的顶点坐标为(1,0).
故答案为(1,0).
6.解:二次函数y=a(x﹣h)2的对称轴是直线x=h,顶点坐标是(h,0).
故答案为:直线x=h,(h,0).
7.解:∵抛物线有最高点,
∴a<0,
∵最高点的横坐标为2,
∴对称轴为x=2,
∴x>2时,y随x的增大而减小.
故答案为x>2.
三、解答题
8.解:(1)二次函数y=﹣(x﹣2)2的图象为:
( http: / / www.21cnjy.com )
开口向下,对称轴为直线x=2,顶点坐标为(2,0);
(2)当x<2时,y随x的增大而增大;
当x>2时,y随x的增大而减小.
9.解:根据题意,由于抛物线经过经过点(﹣3,2)、(﹣1,0),
则有:;
解得,
∴这个二次函数的解析式为y=﹣(x+1)2.
10.
解:(1)抛物线的对称轴为直线x=﹣1.
(2)填表如下:
x … ﹣7 ﹣5 ﹣3 ﹣1 1 3 5 …
y … ﹣9 ﹣4 ﹣1 0 ﹣1 ﹣4 ﹣9 …
(3)描点作图如下:
( http: / / www.21cnjy.com )
11.解:已知抛物线y=a(x﹣h)2的对称轴为直线x=﹣2,
∴h=﹣2,
抛物线y=a(x+2)2与y轴交于点(0,2),
把(0,2)代入y=a(x+2)2得4a=2,
解得a=.
12.解:(1)三个函数的图象如图所示:
( http: / / www.21cnjy.com )
(2)由图象可知函数y=x2开口向上,对称轴为x=0,顶点坐标为(0,0);
函数y=(x+3)2开口向上,对称轴为x=﹣3,顶点坐标为(﹣3,0);
函数y=(x﹣3)2(1)开口向上,对称轴为x=3,顶点坐标为(3,0).
13.解:∵抛物线y=a(x﹣h)2向右平移3个单位,
∴得到的抛物线解析式y=a(x﹣h﹣3)2,
即a=2,
又x﹣h﹣3=x+1,
∴h=﹣4,
∴a=2,h=﹣4.
一、学习目标 会用描点法画出二次函数y=a(x-h)2的图象,能通过图象和关系式认识二次函数的性质;通过独立思考、小组合作、动手操作,掌握二次函数y=a(x-h)2的性质,并会灵活应用.
二、知识回顾 1.二次函数y=ax2,y=ax2+k图象是什么?抛物线.2.二次函数y=ax2+k的图象是由二次函数y=ax2的图象怎样运动得到?若k>0,抛物线y=ax2向上平移k个单位得抛物线y=ax2+k;若k<0,抛物线y=ax2向下平移个单位得抛物线y=ax2+k.3.二次函数y=ax2,y=ax2+k的性质有哪些?请填写下表.函数开口方向对称轴顶点坐标y的最值y=ax2a>0向上y轴(0,0)最小值是0a<0向下y轴(0,0)最大值是0y=ax2+ka>0向上y轴(0,k)最小值是ka<0向下y轴(0,k)最大值是k
三、新知讲解 二次函数y=a(x-h) 的图象与性质 ( http: / / www.21cnjy.com )
四、典例探究 扫一扫,有惊喜哦!1.考查抛物线y=a(x-h) 开口方向、对称轴和顶点坐标【例1】抛物线y=﹣3(x﹣1)2的开口向 ,对称轴是 ,顶点坐标是 .总结:函数y=ax2与y=a(x-h) 的图象开口方向相同,对称轴和顶点坐标不同.函数y=a(x-h) 的对称轴是直线x=h,顶点坐标是(h,0).练1.抛物线y=(x﹣1)2的开口向 ,顶点是 ,对称轴是 .2.考查二次函数y=a(x-h) 的增减性【例2】(2012 石鼓区校级一模)已知二次函数y=(x﹣2)2,当x 时,y随x增大而减小.总结:1.当a>0时,在对称轴(x=h)的左侧 ( http: / / www.21cnjy.com ),y随着x的增大而减小;在对称轴(x=h)右侧,y随着x的增大而增大;当x=h时函数y的值最小(是0).2.当a<0时,在对称轴(x=h)的左侧, ( http: / / www.21cnjy.com )y随着x的增大而增大;在对称轴(x=h)的右侧,y随着x增大而减小;当x=h时,函数y的值最大(是0).练2.二次函数y=﹣(x+3)2,当x 时, y随x的增大而增大,当x 时,随x的增大而减小.3.考查抛物线y=a(x-h) 和y=ax 之间的平移规律【例3】将抛物线y=x2向右平移2个单位,得到新抛物线的表达式是 .总结:1.抛物线的平移不改变二次项的系数,主要是移动顶点位置.2.抛物线y=ax 向右平移h(h>0)个 ( http: / / www.21cnjy.com )单位得到抛物线y=a(x-h) , y=ax 向左平移h(h>0)个单位得到抛物线y=a(x+h) ,简称“左加右减”.练3.(2013 崇明县一模)将抛物线y=(x+1)2向右平移2个单位,得到新抛物线的顶点坐标是 .
五、课后小测 一、选择题1.(2015 嘉定区一模)对于抛物线y=(x﹣2)2,下列说法正确的是( )A.顶点坐标是(2,0) B.顶点坐标是(0,2)C.顶点坐标是(﹣2,0) D.顶点坐标是(0,﹣2)2.(2013秋 泗洪县期末)抛物线y=(x+1)2的顶点坐标是( )A.(﹣1,0) B.(1,0) C.(0,1) D.(0,﹣1)二、填空题3.抛物线y=﹣(x+1) ( http: / / www.21cnjy.com )2的开口 ,对称轴是 ,顶点坐标是 ,它可以看作是由抛物线y=﹣x2向 平移 个单位长度得到的.4.(2014秋 荔湾区期末)将抛物线y=﹣2x2向右平移2个单位,得到的抛物线的解析式是 .5. 将抛物线y=-3x2向左平移2个单位,得到新抛物线的顶点坐标是 .6.(2013秋 沈丘县校级月考)二次函数y=a(x﹣h)2的对称轴是 ,顶点坐标是 .7.已知抛物线y=a(x﹣h)2的最高点的横坐标为2,当x 时,y随x的增大而减小.三、解答题8.(2014秋 丹江口市校级月考)已知二次函数y=﹣(x﹣2)2.(1)画出函数图象,确定抛物线的开口方向、顶点坐标和对称轴;(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小? ( http: / / www.21cnjy.com )9.已知抛物线y=a(x﹣h)2经过点(﹣3,2)、(﹣1,0),求该抛物线的解析式.10.(2012 淄博)已知:抛物线.(1)写出抛物线的对称轴;(2)完成下表;x…﹣7﹣313…y…﹣9﹣1…(3)在下面的坐标系中描点画出抛物线的图象. ( http: / / www.21cnjy.com )11.已知抛物线y=a(x﹣h)2的对称轴为直线x=﹣2,且抛物线与y轴交于点(0,2),求a,h的值.12.已知,函数y=x2,y=(x+3)2和y=(x﹣3)2(1)在同一直角坐标系中画出它们的图象;(2)分别说出各个函数图象的开口方向,对称轴和顶点坐标.13.(2010秋 安庆期末)已知抛物线y=a(x﹣h)2向右平移3个单位后,得到抛物线y=2(x+1)2,求a、h的值.
典例探究答案
【例1】
分析:已知抛物线解析式为顶点式,可根据顶点式求抛物线的开口方向,对称轴及顶点坐标.
解答:解:由y=﹣3(x﹣1)2可知,二次项系数为﹣3<0,
∴抛物线开口向下,对称轴为直线x=1,
顶点坐标为(1,0).
故本题答案为:向下,x=1,(1,0).
点评:本题考查了二次函数解析式的顶点式与其性质的联系,根据二次项系数的符号确定开口方向,根据顶点式确定顶点坐标及对称轴.
练1.
分析:根据二次函数的性质分别填空即可.
解答:解:抛物线y=(x﹣1)2的开口向下,
顶点是(1,0),
对称轴是直线x=1.
故答案为:下,(1,0),直线x=1.
点评:本题考查了二次函数的性质,主要是利用顶点式解析式求解顶点坐标和对称轴的方法,需熟记.
【例2】
分析:根据函数解析式可知,开口方向向上,在对称轴的左侧y随x的增大而减小,在对称轴的右侧,y随x的增大而增大.
解答:解:∵函数的对称轴为x=2,
又∵二次函数开口向上,
∴在对称轴的左侧y随x的增大而减小,
∴x<2时,y随x增大而减小.
故答案为x<2.
点评:本题考查了二次函数的性质,能根据解析式推知函数图象是解题的关键,另外要能准确判断出函数的对称轴.
练2.
分析:利用二次函数的性质求解即可.
解答:解:∵函数y=﹣(x+3)2的对称轴为x=﹣3,且开口向下,
∴当x<﹣3时,函数y=﹣(x+3)2y随x的增大而增大,当x>﹣3时,随x的增大而减小.
故答案为:<﹣3,>﹣3.
点评:本题主要考查了二次函数的性质,解题的关键是熟记二次函数的性质.
【例3】
分析:可根据二次函数图象左加右减,上加下减的平移规律进行解答.
解答:解:二次函数y=x2的图象向右平移2个单位,
得:y=(x﹣2)2,
故答案为:y=(x﹣2)2.
点评:主要考查的是函数图象的平移,用平移规律“左加右减,上加下减”直接代入函数解析式求得平移后的函数解析式.
练3.
分析:先根据y=(x+1)2得到顶点(-1,0),然后把顶点(-1,0)向右平移2个单位即可得到平移后抛物线的顶点坐标.
解答:∵y=(x+1)2的顶点坐标为(﹣1,0),
∴抛物线y=(x+1)2向右平移2个单位后所得抛物线的顶点坐标为(1,0).
故答案为(1,0).
点评:本题考查了二次函数的图象与几何变换:先找到二次函数y=ax2的顶点,然后把抛物线的平移问题转化为顶点的平移问题.
课后小测答案:
一、选择题
1.解:抛物线y=(x﹣2)2的顶点坐标为(2,0),
故选A.
2.解:由抛物线的顶点坐标可知,抛物线y=(x+1)2的顶点坐标是(﹣1,0).
故选A.
二、填空题
3.解:抛物线y=﹣(x+1)2的开口 ( http: / / www.21cnjy.com )向下,对称轴是直线x=﹣1,顶点坐标是(﹣1,0),它可以看作是由抛物线y=﹣x2向左平移1个单位长度得到的.
故答案为:向下,直线x=﹣1,(﹣1,0),左,1.
4.解:抛物线y=﹣2x2向右平移2个单位后的函数抛物线的解析式为:y=﹣2(x﹣2)2.
故答案是:y=﹣2(x﹣2)2.
5.解:∵y=-3x2的顶点坐标为(0,0),
∴抛物线y=-3x2向左平移2个单位后所得抛物线的顶点坐标为(1,0).
故答案为(1,0).
6.解:二次函数y=a(x﹣h)2的对称轴是直线x=h,顶点坐标是(h,0).
故答案为:直线x=h,(h,0).
7.解:∵抛物线有最高点,
∴a<0,
∵最高点的横坐标为2,
∴对称轴为x=2,
∴x>2时,y随x的增大而减小.
故答案为x>2.
三、解答题
8.解:(1)二次函数y=﹣(x﹣2)2的图象为:
( http: / / www.21cnjy.com )
开口向下,对称轴为直线x=2,顶点坐标为(2,0);
(2)当x<2时,y随x的增大而增大;
当x>2时,y随x的增大而减小.
9.解:根据题意,由于抛物线经过经过点(﹣3,2)、(﹣1,0),
则有:;
解得,
∴这个二次函数的解析式为y=﹣(x+1)2.
10.
解:(1)抛物线的对称轴为直线x=﹣1.
(2)填表如下:
x … ﹣7 ﹣5 ﹣3 ﹣1 1 3 5 …
y … ﹣9 ﹣4 ﹣1 0 ﹣1 ﹣4 ﹣9 …
(3)描点作图如下:
( http: / / www.21cnjy.com )
11.解:已知抛物线y=a(x﹣h)2的对称轴为直线x=﹣2,
∴h=﹣2,
抛物线y=a(x+2)2与y轴交于点(0,2),
把(0,2)代入y=a(x+2)2得4a=2,
解得a=.
12.解:(1)三个函数的图象如图所示:
( http: / / www.21cnjy.com )
(2)由图象可知函数y=x2开口向上,对称轴为x=0,顶点坐标为(0,0);
函数y=(x+3)2开口向上,对称轴为x=﹣3,顶点坐标为(﹣3,0);
函数y=(x﹣3)2(1)开口向上,对称轴为x=3,顶点坐标为(3,0).
13.解:∵抛物线y=a(x﹣h)2向右平移3个单位,
∴得到的抛物线解析式y=a(x﹣h﹣3)2,
即a=2,
又x﹣h﹣3=x+1,
∴h=﹣4,
∴a=2,h=﹣4.
同课章节目录
