【多媒体导学案】人教版数学九年级上册第22章第7课时二次函数的图象与各项系数之间的关系(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第22章第7课时二次函数的图象与各项系数之间的关系(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 844.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-15 00:00:00 | ||
图片预览


文档简介
一、学习目标 通过观察二次函数的图象的形成过程,导出二次函数的图象与系数的关系;能根据字母间的关系判断二次函数的性质;理解和探索相关二次函数的图象之间的关系.
二、知识回顾 1.抛物线y=ax2+bx+c的开口方向与什么有关 与二次项系数a.2.抛物线y=ax2+bx+c与y轴的交点坐标是(0,c).3.抛物线y=ax2+bx+c的对称轴是.
三、新知讲解 1.二次函数图象与的关系二次项系数,决定了抛物线开口的大小和方向:a的正负决定开口方向,的大小决定开口的大小.(1)当a>0时,抛物线开口向上;当a<0时,抛物线开口向下;(2)的值越大,开口越小,反之,的值越小,开口越大.2.a,b决定抛物线对称轴的位置抛物线y=ax2+bx +c的对称轴是直线.当b=0时,对称轴为y轴;当(即a,b异号)时,对称轴在y轴右侧;当(即,同号)时,对称轴在y轴左侧.3.决定抛物线与y轴交点的位置当c=0时,抛物线经过原点;当c>0时,抛物线与y轴交于正半轴;当c<0时,抛物线与y轴交于负半轴.4.b2-4ac决定抛物线与x轴交点的个数当b2-4ac>0时,抛物线与x轴有两个交点;当b2-4ac=0时,抛物线与x轴有一个交点;当b2-4ac<0时,抛物线与x轴没有交点.5.a+b+c的符号因为x=1时,y=ax2+bx+c=a+b+c,所以a+b+c的符号由x=1时对应的y值决定.如:(1)当x=1时,若y>0,则a+b+c>0;(2)当x=1时,若y=0,则a+b+c=0;(3)当x=1时,若y<0,则a+b+c<0.6.a-b+c的符号因为x=-1时,y=ax2+bx+c=a-b+c,所以a-b+c的符号由x=-1时对应的y值决定.如:(1)当x=-1时,若y>0,则a-b+c>0;(2)当x=-1时,若y=0,则a-b+c=0;(3)当x=-1时,若y<0,则a-b+c<0.
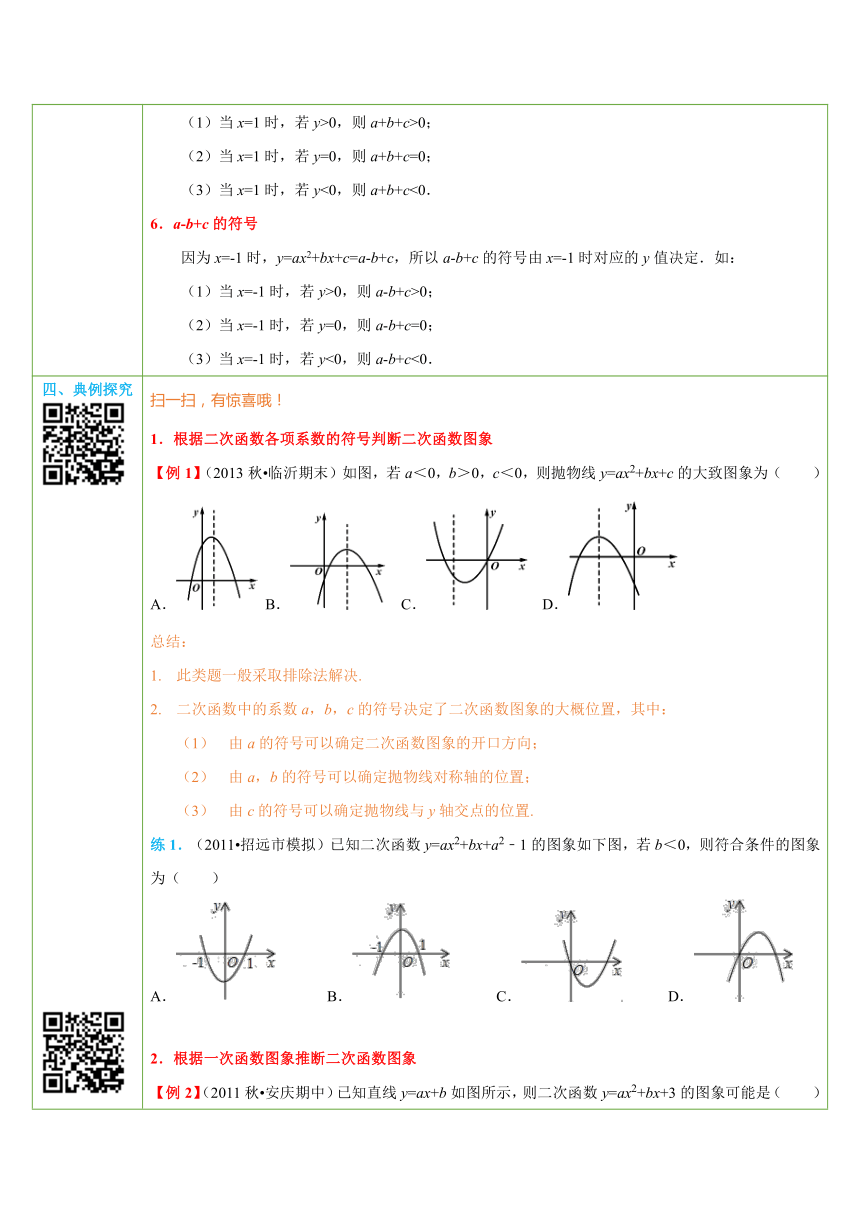
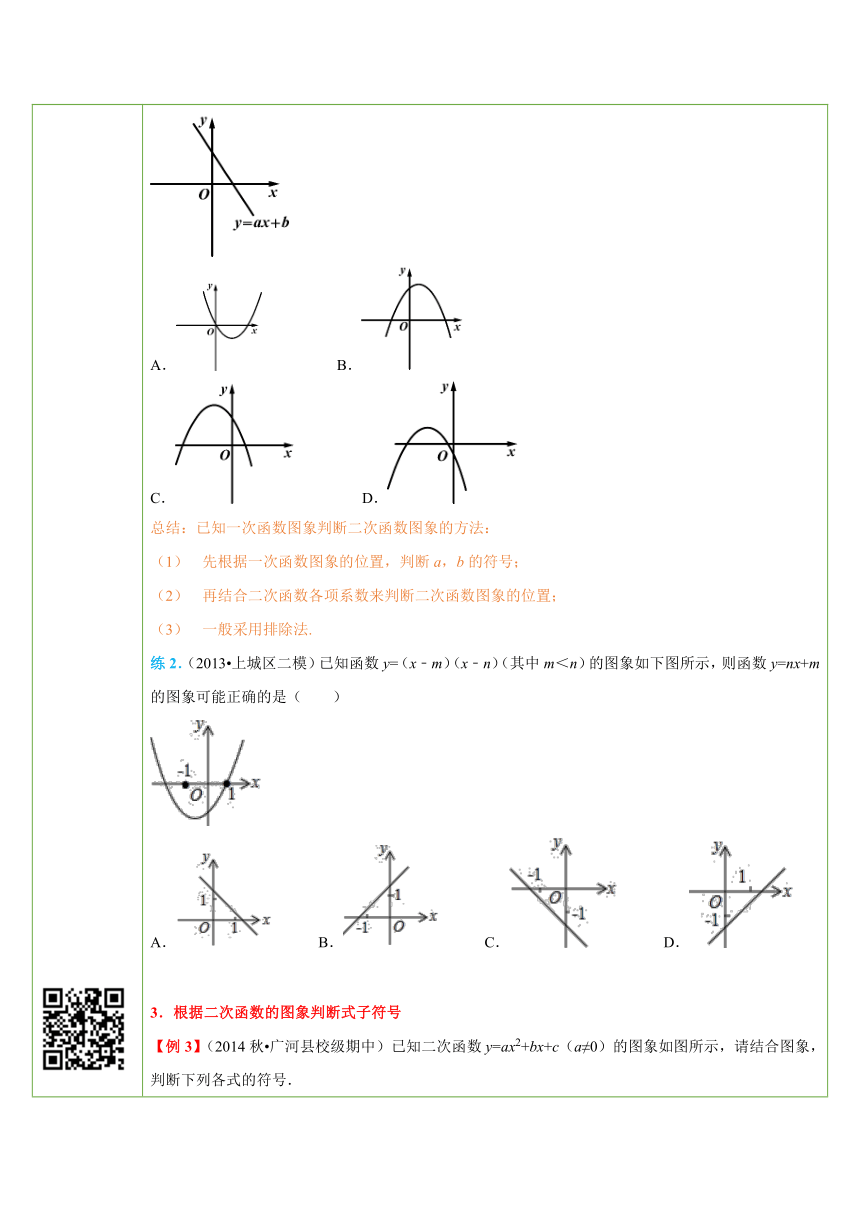
四、典例探究 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) 扫一扫,有惊喜哦!1.根据二次函数各项系数的符号判断二次函数图象【例1】(2013秋 临沂期末)如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )总结:此类题一般采取排除法解决.二次函数中的系数a,b,c的符号决定了二次函数图象的大概位置,其中:由a的符号可以确定二次函数图象的开口方向;由a,b的符号可以确定抛物线对称轴的位置;由c的符号可以确定抛物线与y轴交点的位置.练1.(2011 招远市模拟)已知二次函数y=ax2+bx+a2﹣1的图象如下图,若b<0,则符合条件的图象为( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )2.根据一次函数图象推断二次函数图象【例2】(2011秋 安庆期中)已知直线y=ax+b如图所示,则二次函数y=ax2+bx+3的图象可能是( ) ( http: / / www.21cnjy.com )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )总结:已知一次函数图象判断二次函数图象的方法:先根据一次函数图象的位置,判断a,b的符号;再结合二次函数各项系数来判断二次函数图象的位置;一般采用排除法.练2.(2013 上城区二模)已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如下图所示,则函数y=nx+m的图象可能正确的是( ) ( http: / / www.21cnjy.com )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )3.根据二次函数的图象判断式子符号【例3】(2014秋 广河县校级期中)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,请结合图象,判断下列各式的符号.①abc;②b2﹣4ac;③a+b+c;④a﹣b+c. ( http: / / www.21cnjy.com )总结:已知抛物线y=ax2+bx+c的图象,可以得到以下信息(1)a的符号:由抛物线的开口方向确定;(2)c的符号:由抛物线与y轴的交点位置确定;(3)b的符号:由a及对称轴的位置确定;(4)b2-4ac的符号:由抛物线与x轴的交点个数确定;(5)a+b+c的符号:由x=1时抛物线上的点的位置确定;(6)a-b+c的符号:由x=-1时抛物线上的点的位置确定;(7)2a±b的符号:由对称轴的位置及直线x=1 或x=-1的位置共同确定.练3.(2014 资阳一模)如图是二次函数y=ax2+bx+c图象的一部分,对称轴x=1,给出四个结论:①abc>0;②2a+b=0;③b2>4ac;④a﹣b+c<0.其中正确结论个数是( ) ( http: / / www.21cnjy.com )A.0 B.1 C.2 D.3
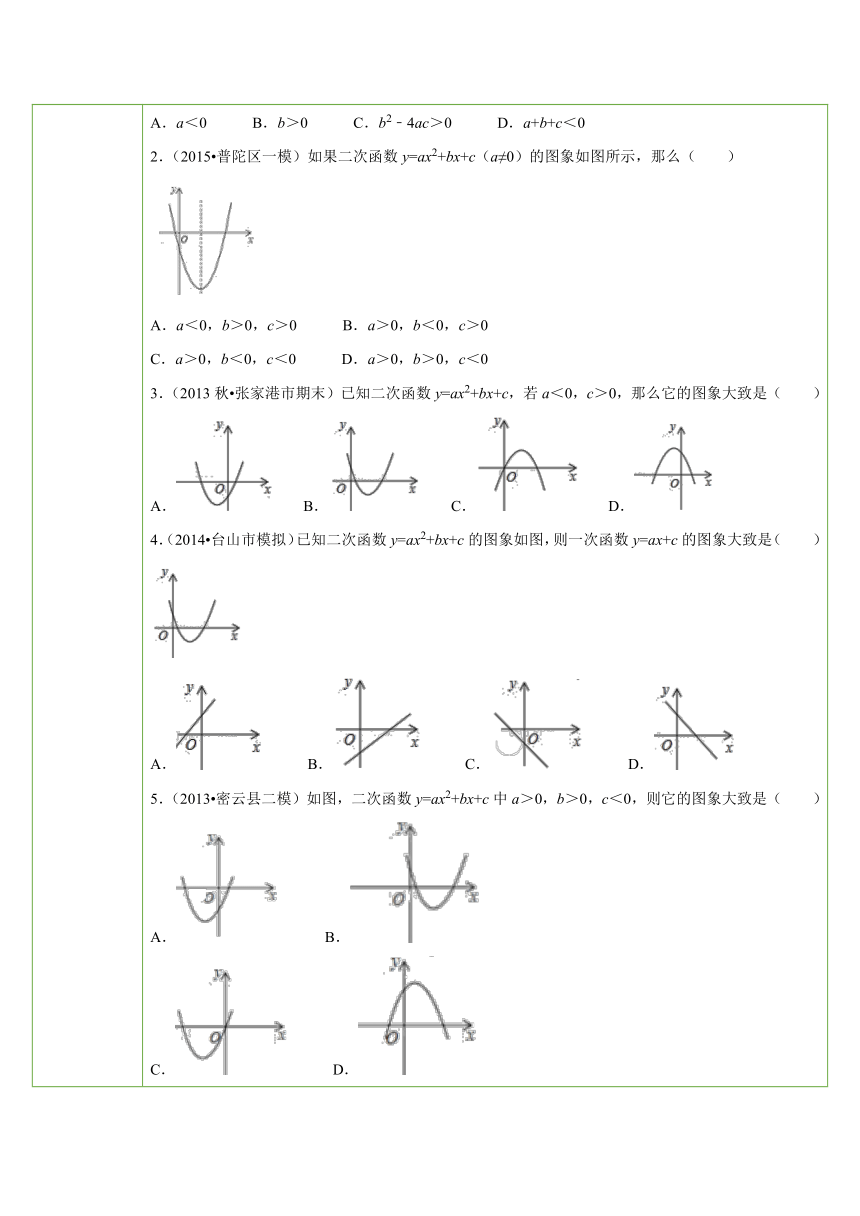
五、课后小测 一、选择题1.(2015 毕节市)二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( ) ( http: / / www.21cnjy.com )A.a<0 B.b>0 C.b2﹣4ac>0 D.a+b+c<02.(2015 普陀区一模)如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( ) ( http: / / www.21cnjy.com )A.a<0,b>0,c>0 B.a>0,b<0,c>0C.a>0,b<0,c<0 D.a>0,b>0,c<03.(2013秋 张家港市期末)已知二次函数y=ax2+bx+c,若a<0,c>0,那么它的图象大致是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )4.(2014 台山市模拟)已知二次函数y=ax2+bx+c的图象如图,则一次函数y=ax+c的图象大致是( ) ( http: / / www.21cnjy.com )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )5.(2013 密云县二模)如图,二次函数y=ax2+bx+c中a>0,b>0,c<0,则它的图象大致是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )6.(2012 常德模拟)当a>0,b<0,函数y=ax2+bx与函数y=ax+b的图象是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )7.(2012 鞍山三模)在同一直角坐标系内,二次函数y1=ax2+bx+c与y2=cx2+bx+a的图象大致为( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )8.(2012秋 萧山区校级月考)已知:a>0,b<0,c<0,则二次函数y=a(x+b)2+c的图象可能是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )9.(2011 枣阳市自主招生)二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( ) ( http: / / www.21cnjy.com )A.b2﹣4ac>0 B.a﹣b+c<0 C.abc<0 D.2a+b>010.(2011 绵阳校级自主招生)已知 ( http: / / www.21cnjy.com )二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0.其中所有正确结论的序号是( ) ( http: / / www.21cnjy.com )A.③④ B.②③ C.①④ D.①②③11.(2009秋 河西区期末)已知二次函数y=ax2+bx+c的系数满足abc<0,则它的图象可能是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. 12.(2015春 鼓楼区校级月考)已知二 ( http: / / www.21cnjy.com )次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=0.5,判断点(a+b+c,abc)在第( )象限. ( http: / / www.21cnjy.com )A.一 B.二 C.三 D.四二、解答题13.已知函数y=ax2+bx+c,若a>0,b<0,c<0,问这个函数的图象与x轴交点情况.14.二次函数y=ax2+bx+c的图象如图所示,以下结论正确的有哪些?并说明理由. ( http: / / www.21cnjy.com )(1)3a+b>0;(2)0<b<a+1;(3)b+2a>0;(4)﹣<a<﹣.
典例探究答案:
【例1】
分析:由抛物线的开口方向判断a的符号,由抛 ( http: / / www.21cnjy.com )物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0,b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B.
点评:考查二次函数y=ax2+bx+c的图象与系数符号的关系.
练1.
分析:由抛物线的开口向下可知a的符号,由对称轴为x=<0可以推出b的取值范围,然后即可作出选择.
解答:解:∵选项A,B对称轴为y轴,
∴对称轴为x==0,即b=0,故此选项错误;
C、∵抛物线开口向上,x=>0
∴a、b异号,
即b<0.故此选项正确;
D、∵抛物线开口向下,x=>0
∴a、b异号,
即b>0.故此选项错误;
故选:C.
点评:本题考查的是二次函数的图象与系数的关系,根据对称轴符号以及a的符号得出是解题关键.
【例2】
分析:利用一次函数图象得出a,b的符号进而得出二次函数开口方向和对称轴位置,即可得出答案.
解答:解:已知直线y=ax+b如图所示:
( http: / / www.21cnjy.com )
故a<0,b>0,
∵a,b异号,
∴二次函数对称轴在x轴正半轴,
且开口向下,
故选:B.
点评:此题主要考查了一次函数与二次函数图象与系数的关系,熟练利用一次函数性质得出a,b符号是解题关键.
练2.
分析:根据图象可得出方程= ( http: / / www.21cnjy.com )(x﹣m)(x﹣n)=0的两个实数根为m,n,且一正一负,又m<n,则m<0<n.根据一次函数y=nx+m的图象的性质即可得出答案.
解答:解:如图,∵函数y=(x﹣m)(x﹣n)(其中m<n),
∴抛物线与x轴的两个交点横坐标分别是m,n,且m<0<n.
∴y=nx+m的图象经过第一、三象限,且与y轴交于负半轴.
故选:D.
点评:本题考查了抛物线与x轴的交点问题以及一次函数的性质,是重点内容要熟练掌握.
【例3】
分析:①抛物线开口向下得到a<0,对称轴在y轴的左侧,a与b同号,得到b<0,抛物线与y轴的交点在x轴的下方得到c<0,于是abc<0;
②抛物线与x轴没有交点,所以△=b2﹣4ac<0;
③取x=1,观察图象得到图象在x轴下方,则x=1,y=a+b+c<0;
④取x=﹣1,观察图象得到图象在x轴下方,则x=﹣1,y=a﹣b+c<0.
解答:解:①抛物线开口向下,则a<0,对称轴在y轴的左侧,则x=<0,则b<0,抛物线与y轴的交点在x轴的下方,则c<0,abc<0;
②抛物线与x轴没有交点,所以△=b2﹣4ac<0;
③当自变量为1时,图象在x轴下方,则x=1时,y=a+b+c<0;
④当自变量为﹣1时,图象在x轴下方,则x=﹣1时,y=a﹣b+c<0.
点评:本题考查了二次函数图象与系数的关系,对于二次函数y=ax2+bx+c(a≠0)的图象:
①二次项系数a决定抛物线的开口方向和大小.
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;
②一次项系数b和二次项系数a共同决定对称轴的位置.
当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右(简称:左同右异);
③常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c).
④抛物线与x轴交点个数.
△=b2﹣4ac>0时,抛物线与x轴有 ( http: / / www.21cnjy.com )2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.
练3.
分析:由抛物线的开口方向判断a与0 ( http: / / www.21cnjy.com )的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:①∵抛物线的开口向上,
∴a>0,
∵与y轴的交点为在y轴的负半轴上,
∴c<0,
∵对称轴为x=>0,
∴a、b异号,即b<0,
∴abc>0;
故本结论正确;
②∵对称轴为x==1,
∴2a=﹣b,
∴2a+b=0;
故本结论正确;
③从图象知,该函数与x轴有两个不同的交点,所以根的判别式△=b2﹣4ac>0,即b2>4ac;
故本结论正确;
④由图象知,x=﹣1时y>0,所以a﹣b+c>0,故本结论错误.
故选D.
点评:本题主要考查图象与二次函数系 ( http: / / www.21cnjy.com )数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式以及特殊值的熟练运用.
课后小测答案:
一、选择题
1.解:A、抛物线开口向下,则a<0,所以A选项的关系式正确;
B、抛物线的对称轴在y轴的右侧,a、b异号,则b>0,所以B选项的关系式正确;
C、抛物线与x轴有2个交点,则△=b2﹣4ac>0,所以D选项的关系式正确;
D、当x=1时,y>0,则a+b+c>0,所以D选项的关系式错误.
故选D.
2.解:∵图象开口方向向上,
∴a>0;
∵图象的对称轴在x轴的正半轴上,
∴>0,
∵a>0,
∴b<0;
∵图象与Y轴交点在y轴的负半轴上,
∴c<0;
∴a>0,b<0,c<0.
故选:C.
3.解:a<0,图象开口向下,故A、B错误;
c>0,图象与y轴的交点在x轴的上方,故C错误;故D正确;
故选:D.
4.解:∵抛物线开口向上,与y轴交于正半轴,
∴a>0,c>0,
∴一次函数y=ax+c的图象经过第一、二、三象限.
故选A.
5.解:∵二次函数y=ax2+bx+c中a>0,
∴该函数图象开口方向向上.
故D错误;
∵二次函数y=ax2+bx+c中a>0,b>0,
∴对称轴x=<0.
故B错误;
∵二次函数y=ax2+bx+c中c<0,
∴该函数图象与y轴交于负半轴,
故C错误.
故选A.
6.解:∵a>0,∴y=ax2+bx图象开口向上,排除C、D;
∵a>0,b<0,∴函数y=ax+b图象经过第一、三、四象限,排除A,
故选B
7.解:A、∵当二次函数y1=ax2+bx+c的图象的开口方向是向下,
∴a<0,
∴二次函数y2=cx2+bx+a与y轴交于负半轴;
故本选项错误;
B、∵当二次函数y1=ax2+bx+c的图象的开口方向是向下,
∴a<0;
又对称轴x=>0,
∴b>0,
而该函数与y轴交于负半轴,
∴c=0;
∴二次函数y2=cx2+bx+a变为一次函数,故本选项错误;
C、∵当二次函数y1=ax2+bx+c的图象的开口方向是向上,
∴a>0,
∴二次函数y2=cx2+bx+a与y轴交于正半轴;
故本选项错误;
D、∵当二次函数y1=ax2+bx+c的图象的开口方向是向上,
∴a>0,此时c<0,
∴二次函数y2=cx2+bx+a与y轴交于正半轴;
故本选项正确.
故选D.
8.解:∵当a>0时,二次函数的图象的开口向上,
∴选项B和C错误;
∵c<0,
∴二次函数的图象的顶点的纵坐标是负数,在x轴的下方,
∴选项A、D都符合,
∵b<0,
∴二次函数的图象的顶点的横坐标是﹣b>0,
即顶点在y轴的右边,
∴选项D错误;只有选项A正确;
故选A.
9.解:A、图象与x轴有2个交点,依据根的判别式可知b2﹣4ac>0,故本选项正确;
B、当x=﹣1时,y=a﹣b+c<0,故本选项正确;
C、∵图象开口向上,∴a>0,
∵与y轴交于负半轴,∴c<0,
∵对称轴在y轴右侧,∴>0,
∴b<0,
∴abc>0,故本选项错误;
D、∵对称轴在1的左边,∴<1,又a>0,∴2a+b>0,故本选项正确.
故选C.
10.解:①当x=1时,y=a+b+c=0,故①错误;
②当x=﹣1时,图象与x轴交点负半轴明显大于﹣1,
∴y=a﹣b+c<0,
故②正确;
③由抛物线的开口向下知a<0,
∵对称轴为0<x=<1,
∴2a+b<0,
故③正确;
④对称轴为x=>0,a<0
∴a、b异号,即b>0,
由图知抛物线与y轴交于正半轴,∴c>0
∴abc<0,
故④错误;
∴正确结论的序号为②③.
故选:B.
11.解:当a>0时,因为abc<0,所以b、c异号,由D图可知c<0,
故b>0,∴<0,即函数对称轴在y轴左侧,选项(D)不符合题意.
由B图可知c>0,故b<0,∴>0,即函数对称轴在y轴右侧,选项(B)不符合题意.
显然a<0时,开口向下,因为abc<0,所以b、c同号,
对于A、由图象可知c>0,则b>0,对称轴>0,即函数对称轴在y轴右侧,A不正确;
对于 C,c>0,则b>0,对称轴>0,C选项正确.
故选C.
12. 解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴b>0,所以A选项错误;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,
∴x=1时,y>0,
∴a+b+c>0,
∴点(a+b+c,abc)在第四象限.
故选D.
二、解答题
13.解:∵△=b2﹣4ac>0,
∴这个函数图象与x轴有两个交点,
设这个函数图象与x轴两个交点的坐标为(x1,0)、(x2,0),
∵x1 x2=,a>0,c<0,
∴x1 x2<0,
∴一个在x轴的正半轴,另一个在x轴的负半轴.
14.解:(1)当图象经过(﹣1,0),(4,0)时,抛物线对称轴为:直线x=,
∵图象经过﹣1与﹣2之间,
∴<,
∴﹣b>3a,
∴3a+b<0,故此选项错误;
(2)当x=﹣1时,a﹣b+c>0,
∵图象经过(0,1),
∴c=1,
∴a﹣b+1>0,
∴a+1>b,
∵对称轴在x轴正半轴,
∴a,b异号,
∵图象开口向下,
∴a<0,
∴b>0,
∴0<b<a+1,此选项正确;
(3)∵图象经过﹣1与﹣2之间,以及(4,0)点,
∴>1,
∴﹣b<2a,
∴2a+b>0,故此选项正确;
(4)当图象过点(﹣1,0),(4,0)时,
设解析式为:y=ax2+bx+1,则,
解得:,
当图象过点(﹣2,0),(4,0)时,
设解析式为:y=ax2+bx+1,则,
解得:,
∴﹣<a<﹣,故此选项正确.
附件1:律师事务所反盗版维权声明
( http: / / www.21cnjy.com )
附件2:独家资源交换签约学校名录(放大查看)
学校名录参见:http://21世纪教育网/wxt/list. aspx ClassID=3060
二、知识回顾 1.抛物线y=ax2+bx+c的开口方向与什么有关 与二次项系数a.2.抛物线y=ax2+bx+c与y轴的交点坐标是(0,c).3.抛物线y=ax2+bx+c的对称轴是.
三、新知讲解 1.二次函数图象与的关系二次项系数,决定了抛物线开口的大小和方向:a的正负决定开口方向,的大小决定开口的大小.(1)当a>0时,抛物线开口向上;当a<0时,抛物线开口向下;(2)的值越大,开口越小,反之,的值越小,开口越大.2.a,b决定抛物线对称轴的位置抛物线y=ax2+bx +c的对称轴是直线.当b=0时,对称轴为y轴;当(即a,b异号)时,对称轴在y轴右侧;当(即,同号)时,对称轴在y轴左侧.3.决定抛物线与y轴交点的位置当c=0时,抛物线经过原点;当c>0时,抛物线与y轴交于正半轴;当c<0时,抛物线与y轴交于负半轴.4.b2-4ac决定抛物线与x轴交点的个数当b2-4ac>0时,抛物线与x轴有两个交点;当b2-4ac=0时,抛物线与x轴有一个交点;当b2-4ac<0时,抛物线与x轴没有交点.5.a+b+c的符号因为x=1时,y=ax2+bx+c=a+b+c,所以a+b+c的符号由x=1时对应的y值决定.如:(1)当x=1时,若y>0,则a+b+c>0;(2)当x=1时,若y=0,则a+b+c=0;(3)当x=1时,若y<0,则a+b+c<0.6.a-b+c的符号因为x=-1时,y=ax2+bx+c=a-b+c,所以a-b+c的符号由x=-1时对应的y值决定.如:(1)当x=-1时,若y>0,则a-b+c>0;(2)当x=-1时,若y=0,则a-b+c=0;(3)当x=-1时,若y<0,则a-b+c<0.
四、典例探究 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) 扫一扫,有惊喜哦!1.根据二次函数各项系数的符号判断二次函数图象【例1】(2013秋 临沂期末)如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )总结:此类题一般采取排除法解决.二次函数中的系数a,b,c的符号决定了二次函数图象的大概位置,其中:由a的符号可以确定二次函数图象的开口方向;由a,b的符号可以确定抛物线对称轴的位置;由c的符号可以确定抛物线与y轴交点的位置.练1.(2011 招远市模拟)已知二次函数y=ax2+bx+a2﹣1的图象如下图,若b<0,则符合条件的图象为( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )2.根据一次函数图象推断二次函数图象【例2】(2011秋 安庆期中)已知直线y=ax+b如图所示,则二次函数y=ax2+bx+3的图象可能是( ) ( http: / / www.21cnjy.com )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )总结:已知一次函数图象判断二次函数图象的方法:先根据一次函数图象的位置,判断a,b的符号;再结合二次函数各项系数来判断二次函数图象的位置;一般采用排除法.练2.(2013 上城区二模)已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如下图所示,则函数y=nx+m的图象可能正确的是( ) ( http: / / www.21cnjy.com )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )3.根据二次函数的图象判断式子符号【例3】(2014秋 广河县校级期中)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,请结合图象,判断下列各式的符号.①abc;②b2﹣4ac;③a+b+c;④a﹣b+c. ( http: / / www.21cnjy.com )总结:已知抛物线y=ax2+bx+c的图象,可以得到以下信息(1)a的符号:由抛物线的开口方向确定;(2)c的符号:由抛物线与y轴的交点位置确定;(3)b的符号:由a及对称轴的位置确定;(4)b2-4ac的符号:由抛物线与x轴的交点个数确定;(5)a+b+c的符号:由x=1时抛物线上的点的位置确定;(6)a-b+c的符号:由x=-1时抛物线上的点的位置确定;(7)2a±b的符号:由对称轴的位置及直线x=1 或x=-1的位置共同确定.练3.(2014 资阳一模)如图是二次函数y=ax2+bx+c图象的一部分,对称轴x=1,给出四个结论:①abc>0;②2a+b=0;③b2>4ac;④a﹣b+c<0.其中正确结论个数是( ) ( http: / / www.21cnjy.com )A.0 B.1 C.2 D.3
五、课后小测 一、选择题1.(2015 毕节市)二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( ) ( http: / / www.21cnjy.com )A.a<0 B.b>0 C.b2﹣4ac>0 D.a+b+c<02.(2015 普陀区一模)如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( ) ( http: / / www.21cnjy.com )A.a<0,b>0,c>0 B.a>0,b<0,c>0C.a>0,b<0,c<0 D.a>0,b>0,c<03.(2013秋 张家港市期末)已知二次函数y=ax2+bx+c,若a<0,c>0,那么它的图象大致是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )4.(2014 台山市模拟)已知二次函数y=ax2+bx+c的图象如图,则一次函数y=ax+c的图象大致是( ) ( http: / / www.21cnjy.com )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )5.(2013 密云县二模)如图,二次函数y=ax2+bx+c中a>0,b>0,c<0,则它的图象大致是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )6.(2012 常德模拟)当a>0,b<0,函数y=ax2+bx与函数y=ax+b的图象是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )7.(2012 鞍山三模)在同一直角坐标系内,二次函数y1=ax2+bx+c与y2=cx2+bx+a的图象大致为( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )8.(2012秋 萧山区校级月考)已知:a>0,b<0,c<0,则二次函数y=a(x+b)2+c的图象可能是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )9.(2011 枣阳市自主招生)二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( ) ( http: / / www.21cnjy.com )A.b2﹣4ac>0 B.a﹣b+c<0 C.abc<0 D.2a+b>010.(2011 绵阳校级自主招生)已知 ( http: / / www.21cnjy.com )二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0.其中所有正确结论的序号是( ) ( http: / / www.21cnjy.com )A.③④ B.②③ C.①④ D.①②③11.(2009秋 河西区期末)已知二次函数y=ax2+bx+c的系数满足abc<0,则它的图象可能是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. 12.(2015春 鼓楼区校级月考)已知二 ( http: / / www.21cnjy.com )次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=0.5,判断点(a+b+c,abc)在第( )象限. ( http: / / www.21cnjy.com )A.一 B.二 C.三 D.四二、解答题13.已知函数y=ax2+bx+c,若a>0,b<0,c<0,问这个函数的图象与x轴交点情况.14.二次函数y=ax2+bx+c的图象如图所示,以下结论正确的有哪些?并说明理由. ( http: / / www.21cnjy.com )(1)3a+b>0;(2)0<b<a+1;(3)b+2a>0;(4)﹣<a<﹣.
典例探究答案:
【例1】
分析:由抛物线的开口方向判断a的符号,由抛 ( http: / / www.21cnjy.com )物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0,b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B.
点评:考查二次函数y=ax2+bx+c的图象与系数符号的关系.
练1.
分析:由抛物线的开口向下可知a的符号,由对称轴为x=<0可以推出b的取值范围,然后即可作出选择.
解答:解:∵选项A,B对称轴为y轴,
∴对称轴为x==0,即b=0,故此选项错误;
C、∵抛物线开口向上,x=>0
∴a、b异号,
即b<0.故此选项正确;
D、∵抛物线开口向下,x=>0
∴a、b异号,
即b>0.故此选项错误;
故选:C.
点评:本题考查的是二次函数的图象与系数的关系,根据对称轴符号以及a的符号得出是解题关键.
【例2】
分析:利用一次函数图象得出a,b的符号进而得出二次函数开口方向和对称轴位置,即可得出答案.
解答:解:已知直线y=ax+b如图所示:
( http: / / www.21cnjy.com )
故a<0,b>0,
∵a,b异号,
∴二次函数对称轴在x轴正半轴,
且开口向下,
故选:B.
点评:此题主要考查了一次函数与二次函数图象与系数的关系,熟练利用一次函数性质得出a,b符号是解题关键.
练2.
分析:根据图象可得出方程= ( http: / / www.21cnjy.com )(x﹣m)(x﹣n)=0的两个实数根为m,n,且一正一负,又m<n,则m<0<n.根据一次函数y=nx+m的图象的性质即可得出答案.
解答:解:如图,∵函数y=(x﹣m)(x﹣n)(其中m<n),
∴抛物线与x轴的两个交点横坐标分别是m,n,且m<0<n.
∴y=nx+m的图象经过第一、三象限,且与y轴交于负半轴.
故选:D.
点评:本题考查了抛物线与x轴的交点问题以及一次函数的性质,是重点内容要熟练掌握.
【例3】
分析:①抛物线开口向下得到a<0,对称轴在y轴的左侧,a与b同号,得到b<0,抛物线与y轴的交点在x轴的下方得到c<0,于是abc<0;
②抛物线与x轴没有交点,所以△=b2﹣4ac<0;
③取x=1,观察图象得到图象在x轴下方,则x=1,y=a+b+c<0;
④取x=﹣1,观察图象得到图象在x轴下方,则x=﹣1,y=a﹣b+c<0.
解答:解:①抛物线开口向下,则a<0,对称轴在y轴的左侧,则x=<0,则b<0,抛物线与y轴的交点在x轴的下方,则c<0,abc<0;
②抛物线与x轴没有交点,所以△=b2﹣4ac<0;
③当自变量为1时,图象在x轴下方,则x=1时,y=a+b+c<0;
④当自变量为﹣1时,图象在x轴下方,则x=﹣1时,y=a﹣b+c<0.
点评:本题考查了二次函数图象与系数的关系,对于二次函数y=ax2+bx+c(a≠0)的图象:
①二次项系数a决定抛物线的开口方向和大小.
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;
②一次项系数b和二次项系数a共同决定对称轴的位置.
当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右(简称:左同右异);
③常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c).
④抛物线与x轴交点个数.
△=b2﹣4ac>0时,抛物线与x轴有 ( http: / / www.21cnjy.com )2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.
练3.
分析:由抛物线的开口方向判断a与0 ( http: / / www.21cnjy.com )的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:①∵抛物线的开口向上,
∴a>0,
∵与y轴的交点为在y轴的负半轴上,
∴c<0,
∵对称轴为x=>0,
∴a、b异号,即b<0,
∴abc>0;
故本结论正确;
②∵对称轴为x==1,
∴2a=﹣b,
∴2a+b=0;
故本结论正确;
③从图象知,该函数与x轴有两个不同的交点,所以根的判别式△=b2﹣4ac>0,即b2>4ac;
故本结论正确;
④由图象知,x=﹣1时y>0,所以a﹣b+c>0,故本结论错误.
故选D.
点评:本题主要考查图象与二次函数系 ( http: / / www.21cnjy.com )数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式以及特殊值的熟练运用.
课后小测答案:
一、选择题
1.解:A、抛物线开口向下,则a<0,所以A选项的关系式正确;
B、抛物线的对称轴在y轴的右侧,a、b异号,则b>0,所以B选项的关系式正确;
C、抛物线与x轴有2个交点,则△=b2﹣4ac>0,所以D选项的关系式正确;
D、当x=1时,y>0,则a+b+c>0,所以D选项的关系式错误.
故选D.
2.解:∵图象开口方向向上,
∴a>0;
∵图象的对称轴在x轴的正半轴上,
∴>0,
∵a>0,
∴b<0;
∵图象与Y轴交点在y轴的负半轴上,
∴c<0;
∴a>0,b<0,c<0.
故选:C.
3.解:a<0,图象开口向下,故A、B错误;
c>0,图象与y轴的交点在x轴的上方,故C错误;故D正确;
故选:D.
4.解:∵抛物线开口向上,与y轴交于正半轴,
∴a>0,c>0,
∴一次函数y=ax+c的图象经过第一、二、三象限.
故选A.
5.解:∵二次函数y=ax2+bx+c中a>0,
∴该函数图象开口方向向上.
故D错误;
∵二次函数y=ax2+bx+c中a>0,b>0,
∴对称轴x=<0.
故B错误;
∵二次函数y=ax2+bx+c中c<0,
∴该函数图象与y轴交于负半轴,
故C错误.
故选A.
6.解:∵a>0,∴y=ax2+bx图象开口向上,排除C、D;
∵a>0,b<0,∴函数y=ax+b图象经过第一、三、四象限,排除A,
故选B
7.解:A、∵当二次函数y1=ax2+bx+c的图象的开口方向是向下,
∴a<0,
∴二次函数y2=cx2+bx+a与y轴交于负半轴;
故本选项错误;
B、∵当二次函数y1=ax2+bx+c的图象的开口方向是向下,
∴a<0;
又对称轴x=>0,
∴b>0,
而该函数与y轴交于负半轴,
∴c=0;
∴二次函数y2=cx2+bx+a变为一次函数,故本选项错误;
C、∵当二次函数y1=ax2+bx+c的图象的开口方向是向上,
∴a>0,
∴二次函数y2=cx2+bx+a与y轴交于正半轴;
故本选项错误;
D、∵当二次函数y1=ax2+bx+c的图象的开口方向是向上,
∴a>0,此时c<0,
∴二次函数y2=cx2+bx+a与y轴交于正半轴;
故本选项正确.
故选D.
8.解:∵当a>0时,二次函数的图象的开口向上,
∴选项B和C错误;
∵c<0,
∴二次函数的图象的顶点的纵坐标是负数,在x轴的下方,
∴选项A、D都符合,
∵b<0,
∴二次函数的图象的顶点的横坐标是﹣b>0,
即顶点在y轴的右边,
∴选项D错误;只有选项A正确;
故选A.
9.解:A、图象与x轴有2个交点,依据根的判别式可知b2﹣4ac>0,故本选项正确;
B、当x=﹣1时,y=a﹣b+c<0,故本选项正确;
C、∵图象开口向上,∴a>0,
∵与y轴交于负半轴,∴c<0,
∵对称轴在y轴右侧,∴>0,
∴b<0,
∴abc>0,故本选项错误;
D、∵对称轴在1的左边,∴<1,又a>0,∴2a+b>0,故本选项正确.
故选C.
10.解:①当x=1时,y=a+b+c=0,故①错误;
②当x=﹣1时,图象与x轴交点负半轴明显大于﹣1,
∴y=a﹣b+c<0,
故②正确;
③由抛物线的开口向下知a<0,
∵对称轴为0<x=<1,
∴2a+b<0,
故③正确;
④对称轴为x=>0,a<0
∴a、b异号,即b>0,
由图知抛物线与y轴交于正半轴,∴c>0
∴abc<0,
故④错误;
∴正确结论的序号为②③.
故选:B.
11.解:当a>0时,因为abc<0,所以b、c异号,由D图可知c<0,
故b>0,∴<0,即函数对称轴在y轴左侧,选项(D)不符合题意.
由B图可知c>0,故b<0,∴>0,即函数对称轴在y轴右侧,选项(B)不符合题意.
显然a<0时,开口向下,因为abc<0,所以b、c同号,
对于A、由图象可知c>0,则b>0,对称轴>0,即函数对称轴在y轴右侧,A不正确;
对于 C,c>0,则b>0,对称轴>0,C选项正确.
故选C.
12. 解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴b>0,所以A选项错误;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,
∴x=1时,y>0,
∴a+b+c>0,
∴点(a+b+c,abc)在第四象限.
故选D.
二、解答题
13.解:∵△=b2﹣4ac>0,
∴这个函数图象与x轴有两个交点,
设这个函数图象与x轴两个交点的坐标为(x1,0)、(x2,0),
∵x1 x2=,a>0,c<0,
∴x1 x2<0,
∴一个在x轴的正半轴,另一个在x轴的负半轴.
14.解:(1)当图象经过(﹣1,0),(4,0)时,抛物线对称轴为:直线x=,
∵图象经过﹣1与﹣2之间,
∴<,
∴﹣b>3a,
∴3a+b<0,故此选项错误;
(2)当x=﹣1时,a﹣b+c>0,
∵图象经过(0,1),
∴c=1,
∴a﹣b+1>0,
∴a+1>b,
∵对称轴在x轴正半轴,
∴a,b异号,
∵图象开口向下,
∴a<0,
∴b>0,
∴0<b<a+1,此选项正确;
(3)∵图象经过﹣1与﹣2之间,以及(4,0)点,
∴>1,
∴﹣b<2a,
∴2a+b>0,故此选项正确;
(4)当图象过点(﹣1,0),(4,0)时,
设解析式为:y=ax2+bx+1,则,
解得:,
当图象过点(﹣2,0),(4,0)时,
设解析式为:y=ax2+bx+1,则,
解得:,
∴﹣<a<﹣,故此选项正确.
附件1:律师事务所反盗版维权声明
( http: / / www.21cnjy.com )
附件2:独家资源交换签约学校名录(放大查看)
学校名录参见:http://21世纪教育网/wxt/list. aspx ClassID=3060
同课章节目录
